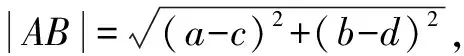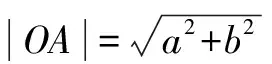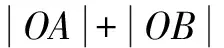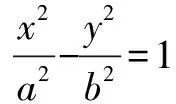灵感源于构造三角形

南京市大厂高级中学(210044) 雷亚庆●



灵感源于构造三角形

南京市大厂高级中学(210044)
雷亚庆●

有些代数问题处理起来无从下手，没有头绪，如果我们能够根据已知条件构造出三角形，把抽象的代数问题转化为三角问题，就会使隐藏的关系直观化，从而发现解题思路，实现难题巧解，下举几例加以说明.

例1 求sin238°+sin282°-sin38°sin82°的值.

解析 构造△ABC,使得A=38°,B=82°,C=60°,设△ABC外接圆直径为2R,则

sin238°+sin282°-sin38°sin82°=sin2A+sin2B-2sinAsinBcosC.

由正弦定理：

sin2A+sin2B-2sinAsinBcosC

解题反思 如果利用三角公式进行化简和求值运算，需要降幂公式和和差化积公式，较繁琐，仔细观察所给角的特征我们发现38°,82°与60°正好构成一个三角形的三个内角，因此考虑构造三角形利用正余弦定理求解.实际上利用归纳推理，大家还可以得到一般性结论: 这实际上是正余弦定理的综合形式：

sin2C=sin2A+sin2B-2sinAsinBcosC.

例2 求tan15°.

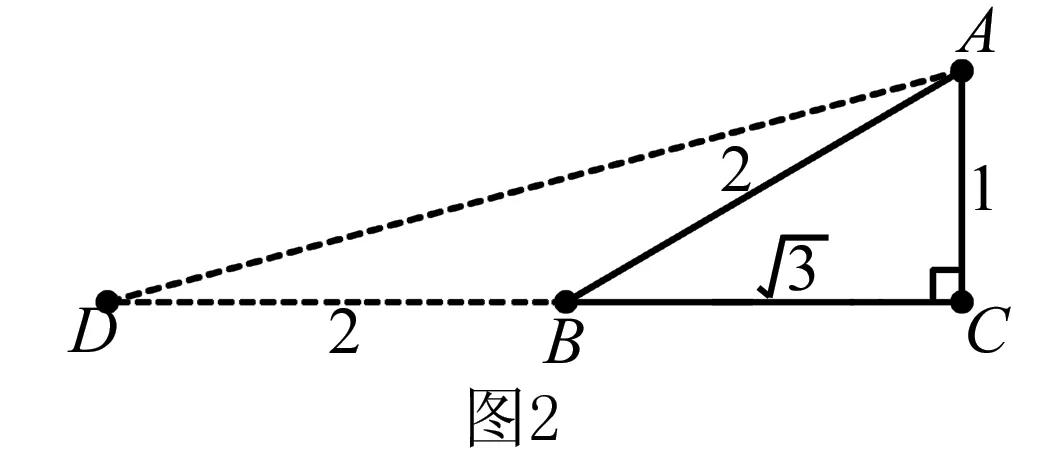
解析 如图2构造Rt△ABC，∠C=90°,AB=2,CA=1,则∠ABC=30°.

延长CB到D,使BD=BA，连AD，则∠ADC=15°

解题反思 先构造含有30° 角的直角三角形，再利用平面几何知识构造出含有15°的直角三角形，利用锐角三角函数的定义轻松解决问题.事实上，如图3我们把结论一般化可以利用构造直角三角形的方法巧妙地记忆正切的半角公式：

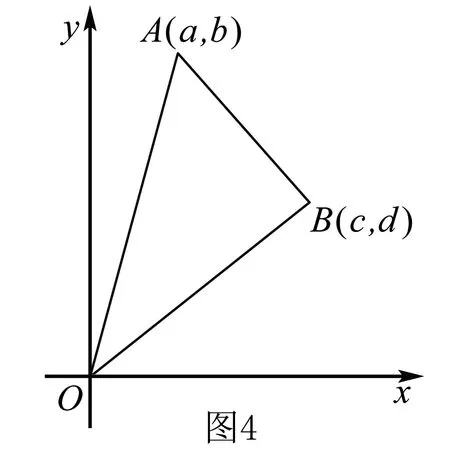
例3 已知a、b、c均为正实数,满足关系式a2+b2=c2,又n为不小于3的自然数，

求证:an+bn

证明 设a、b、c所对的角分别为A、B、C，知C是直角，A为锐角，

因为0

所以n≥3时，有

sinnA

于是有sinnA+cosnA

从而就有an+bn

解题反思 由于这是一个关于自然数n的命题，一些学生都会想到用数学归纳法来证明，实际上由条件a、b、c均为正实数及a2+b2=c2可联想到勾股定理,a、b、c可构成直角三角形的三边，进一步联想到三角函数的定义可得如上证法.

解题反思 很多同学看到这个不等式证明题，马上想到采用分析法、综合法等，而此题利用这些方法证明很繁.从题目的外表形式观察到，要证的结论的右端与平面内两点间的距离公式很相似，而左端可看作是点到原点的距离公式.根据其特点，可构造三角形巧妙而简捷加以证明，这正是思维变通的体现.

由双曲线的第二定义有

解题反思 离心率是圆锥曲线的一个重要的基本量，根据直线与圆锥曲线位置关系求离心率是一个难点.如果我们掌握利用构造直角三角形，利用圆锥曲线的统一定义找到离心率，直线斜率和直角边的关系，就可以顺利求解.而且此类问题也有一般性结论，有兴趣的老师和同学可以自行探究.

由此问题转化为：在线段AB上取一点C，使MC+NC最小.

利用对称性问题得以轻松的解决.答案应为13.

解题反思 本题有点儿那种“数缺形时少直观”的感觉.而且用纯代数方法不易寻得解题思路， 而如果变数为形，构造直角三角形，展示题目特点，利用对称则可轻松获解.

通过构造三角形对上述几个问题的解决告诉我们解题时要注意代数与几何之间的联系，将题目条件的数字或式子特征与直观图形联想起来，通过类比联想、数形结合思想把问题放在三角形中，利用解三角形的知识使解题更加简洁明了.

G632

B

1008-0333(2017)10-0012-02