从递推数列an+1=Aan+φ(A≠1)解题思路想起

广东省深圳市龙岗区龙西学校(518116) 冯远军●



从递推数列an+1=Aan+φ(A≠1)解题思路想起

广东省深圳市龙岗区龙西学校(518116)
冯远军●

一、引例[2006年，重庆14]在数列中， a1=1，an+1=2an+3(n≥1)，则该数列的通项an=____.

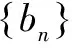
此解题思路是设法把原数列配成一个公比为A的等比数列，这种“配等比”的思路给我们提供了新角度去分析和解决问题.因此可以尝试探究用“配等比”的思路方法，使复杂的递推数列进行“公式化”的解答.

二、思路探究

我们利用“配等比”的方法把型如an+1=Aan+φ(A≠1)的数列作进一步分析：

分析 利用“公式化”解题方法，首先找出A，c，然后计算出g，等比数列就可由这几项更简单地配出来，问题就迎刃而解.

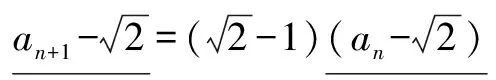
(二)当φ=f(n)，f(n)为k次多项式，即f(n)=α1nk+α2nk-1+…+αkn+αk+1，

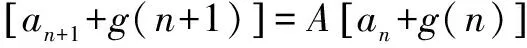
f(n)=α1nk+α2nk-1+…+αkn+αk+1

分析 首先找出A，f(n)，然后计算出β，再计算出g(n).

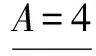
三、应用举例

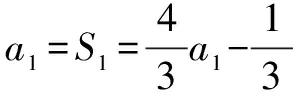
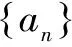
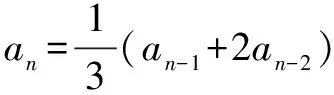
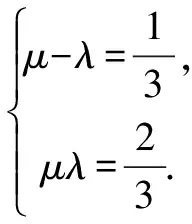
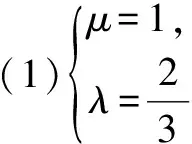
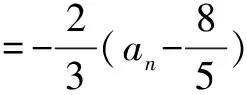
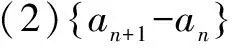
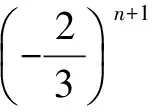
综合上述，(1)和(2)的结果相同，所以原数列有相同解：

G632

B

1008-0333(2017)10-0033-02