一道考题的错解及多种解法

安徽省定远中学高二(1)班(233200) 韩凯钰●



一道考题的错解及多种解法

安徽省定远中学高二(1)班(233200)
韩凯钰●

在一次考试中，有一道选择题自认为做得正确，但试卷发下来，发现是一个红红的叉，静下心来深入思考，不仅找到了错误的原因，还研究出多种解法，很享受，故整理成文，与同学们共享.

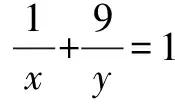
A. 8 B. 12 C. 16 D. 20

考试用的错误解法：

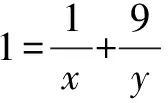
∴xy≥36.

所以x+y的最小值是12.

解法1 发现等号不成立，可知x+y>12，所以可以否定选项A和B.下面只需再否定一个选项就行.可以用x=4，y=12否定选项D.因为x=4,y=12 满足前提条件，说明有一个值是16，所以20不是最小值.

∴x+y>10,∴A错.

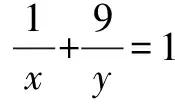
老师说我这两种方法在考试中很管用，排除法、特殊值法对解某些选择题很管用，在考试中，可以用，但平时做题时，应该多思考，从多个角度去找解题方法.在老师的鼓励下，我又进行思考，又有了以下的解法.选C.

设x-1=t,

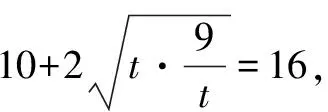
当且仅当t=3即x=4时不等式取等号.

∴(x+y)min=16.

(反思小结:先用代入消元，再换元，最后使用平均值不等式.)

∴x+y=csc2θ+9sec2θ=1+cot2θ+9+tan2θ

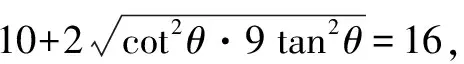
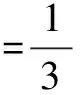
∴(x+y)min=16.

(反思小结:先用三角代换法，再用平均值不等式.)

解法5 设x+y=t，则y=t-x,

∴x2+(8-t)x+t=0.

因为x是实数,

∴Δ=(8-t)2-4t≥0,

∴t≥16或t≤4.

∵x>1,y>9,∴t>10

∴(x+y)min=16.

当t=16时x=4，y=12存在.

(反思小结:先代入消元，再整理成关于x的一元二次方程，最后用判别式法.但判别式法必须保证自变量定义域为全体实数，而变量范围受到控制，所以“当t=16时x=4，y=12存在”这一检验过程不可少)

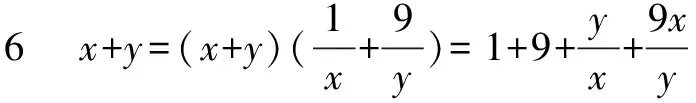
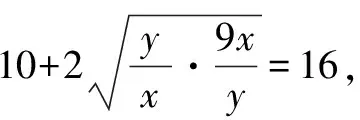
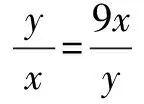
∴(x+y)min=16.

通过对这题的深入思考，发现了多种解法，锻炼了我的思维，今后再遇到错题，请同学们与我一样，认真思考，去发现数学的奥秘，你会觉得数学是有趣的.

G632

B

1008-0333(2017)10-0040-01