高中三角函数高考试题分析及教学策略研究
2017-05-17广东省惠州市第八中学516000
广东省惠州市第八中学(516000) 罗 为●
高中三角函数高考试题分析及教学策略研究
广东省惠州市第八中学(516000)
罗 为●
三角函数在高考中的比重较大,是高中教学中的重要知识点.考试题目主要针对学生对三角函数性质的理解和应用能力,在教学中,教师应该结合往年的高考试题,并根据学生的实际情况制定正确的教学策略,以此不断提高教学质量,为学生高考奠定良好的基础.
三角函数;高中;教学策略;高考
三角函数这一部分知识内容在高中数学的教学中占据着十分重要的地位,可以说,函数部分对学生高考成绩起到了巨大的影响.虽然目前函数的题目类型大同小异,主要针对的都是学生对函数的理解、应用能力.但是,许多学生因为受到思维方式上的影响,在该部分内容的学习中仍然存在很多问题,不能正确理解函数的基本概念,更不能做到灵活应用到解题过程中.所以这就需要教师结合学生的实际情况,制定合理的教学策略.
一、将三角函数与其他知识内容结合
新课程改革要求教师在高中数学教学中改变传统的教学方式,让学生能够将所有知识点紧密地联系在一起,不断提升解题过程中的综合能力.三角函数这一知识内容本就和其他知识点联系紧密,教师在教学中也应该特别注意这一问题,制定合理的教学策略增加学生知识融合和综合运用的机会,将三角函数与其他知识内容之间相互关联,提升学生综合理解能力和解题能力,实现教学目标.
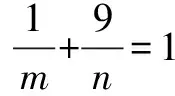
这道题目就是我们在考试中经常会在选择题类型中碰到的综合性题目,它将三角函数的知识内容和代数知识融合在一起.

结合cos2α+sin2α=1这一基本公式,则有
m+n=sec2α+9csc2α=10+(tan2α+9cot2α)
≥10+6=16.
当且仅当tan2α=9cot2αtan2α=3时等号成立.
这道题目将三角函数的知识内容和换元法结合在一起,极大地减少了代数题目中巨大的计算压力,可以有效提升学生的解题效率.
二、注重学生思维能力的培养
部分教师在过去的三角函数教学中存在误区,他们认为只要学生做足了大量的题目自然就能够熟练地掌握三角函数的应用.但是,通过长时间的观察我们便可以发现,这种方式对学生来说并不是十分有效.三角函数的学习对学生思维能力要求较高,因此,教师需要改变过去的题海战术,将重点放在学生思维能力的培养上,让他们在解题过程中能够冷静思考并主动从不同角度上去思考问题.
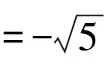
这道高考题目看似十分简单,大多数学生都能够找到题目的答案.因此,在这道题目的分析过程中,教师的重点应该放在学生的思维拓展上,让他们尽可能多地找到解题方法.



解法2 将已知等式两边同时平方可得
cos2α+4cosαsinα+4sin2α=5=5(sin2α+cos2α)
⟹sin2α-4sinαcosα+4cos2α=0
⟹tan2α-4tanα+4=0,
所以tanα=2.
解法3 令sinα-2cosα=t,由题目的已知可以求得5=5+t2,所以t为0.
也就是sinα-2cosα=0,所以tanα=2.

所以可以求得tanα=2.
这道题目考查的是学生三角恒等式之间的变换能力,教师可以从多个角度分析题目,为学生在解题过程中不断扩宽自己的思维.
三、熟练掌握代入法在三角函数中的应用
在高考数学题目中,代入法是一种常见的解题方式,对于学生自身来说也并不陌生,早在初中函数的学习中,他们就已经接触到了代入法.也正是由于这种解题方式经常出现在高考的题目中,教师也就必须要在教学中帮助学生加深对这一解题方法的印象,能够顺利将其应用到高考中的三角函数题目中.代入法可以提升学生对三角函数的学习兴趣,也是提高学生在高考中解题效率的有效方法.


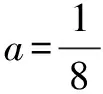

从这道题目的解题过程中我们不难发现,利用代入法解决三角函数问题可以有效简化计算方法,让学生在解题过程中的思路更加清晰.在分析题目的过程中,教师不妨在教学的过程中让学生学会举一反三,让他们利用该方法解决更多的三角函数问题.
四、注重三角函数与图象之间的结合
三角函数的图象和性质之间的结合是高考中必会出现的题目类型,包括了三角函数的最小值、周期、单调性等等内容.因此,教师在题目的讲解中也要时刻将图象和性质结合在一起,并让学生熟记三角函数的性质.

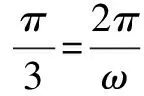
这道题目是典型的图象与性质结合的题目,虽然对学生来说稍微有些灵活,但是却仍然是对学生三角函数基本性质掌握程度的考查.
总之,在高考前的三角函数复习过程中,教师要充分根据学生的实际情况和教学中的要求,结合三角函数的基本要点,制定有效的学习方法,以此不断提升三角函数教学课堂的质量,为学生在高考中取得好的成绩打下基础.
G632
B
1008-0333(2017)10-0035-02
