EuTiO3纳米线的电熵特性研究

徐秋艳， 曹海霞

(苏州大学 物理与光电能源学部， 江苏 苏州 215006)

EuTiO3纳米线的电熵特性研究

徐秋艳， 曹海霞

(苏州大学 物理与光电能源学部， 江苏 苏州 215006)

运用Landau-Ginzburg-Devonshire理论与热力学理论，研究了量子顺电EuTiO3纳米线的电致熵变特性。研究表明在高温铁电-顺磁区域，当ΔE=100 kV/cm，R=0.8 nm时，可获得较大的绝热温度差ΔT=7.4 K；在低温区0～30 K，在一定的表面径向应力、一定的半径尺寸下，EuTiO3纳米线可以实现铁电-铁磁性，在磁相变温度附近，绝热温度差可以达到一个较大的峰值，且峰值随着纳米线半径的增大和表面张量系数的减小而略有增大。当μ=10 N/m，R=1.0 nm时，可获得较大的绝热温度差ΔT=2.2 K。

EuTiO3纳米线； 电熵； Landau-Ginzburg-Devonshire理论

多铁性材料由于在信息存储器、自旋电子器件等方面具有很好的应用前景，受到凝聚态物理和材料物理研究者的广泛关注。量子顺电-反铁磁材料EuTiO3在一定的应力作用下可以实现铁电-铁磁体，从而具有很好的磁电耦合特性。由于多铁性材料中既有磁极化又有电极化，外加电场既改变了电极化又通过磁电耦合效应改变了磁极化，因此多铁性材料中的熵变课题是当前一个热点课题。虽然有实验报道了EuTiO3材料具有较好的磁熵特性，但EuTiO3纳米线的电致熵变特性的研究目前还未见有文献报道过。

多铁性材料是指在一定温区内同时具有(反)铁电序、(反)铁磁序或铁弹序的材料，提供了同时用电极化和磁化来编码储存信息的可能性。同时，由于不同铁性之间的相互耦合而产生新的功能，例如磁电耦合效应，即材料在外磁场作用下产生电极化，或者在外电场作用下产生磁极化的特性，从而可能实现铁电性和磁性的相互调控，为发展新的多功能器件提供机会。近年来随着各种新设备新技术的应用，多重铁性材料引起材料研究者的广泛关注和兴趣，实验上可以制备出多种结构类型的多铁性材料，如钙钛矿型化合物BiFeO3、六角结构化合物YMnO3等。多铁性材料集结了磁、电、力学等信息的耦合、转换等功能，在声纳探测器、信息存储器、自旋电子器件、传感器等高新技术领域具有很好的潜在应用前景，更是蕴涵着丰富的物理研究内容[1]。从凝聚态物理角度看，多铁性现象本身也对铁电学、磁学和强关联电子物理提出了很多基本问题和挑战，成为量子调控研究的一个热点领域，因此无论从理论研究方面还是实验研究角度，对多铁性材料物理特性的研究都具有非常重要的意义。

EuTiO3与典型的量子顺电体SrTiO3相似，是钙钛矿结构的量子顺电体，同时EuTiO3的A位Eu2+(4f7)的局域磁矩(J=S=7/2)在温度低于5.5 K时的排列显示EuTiO3的基态是G型反铁磁，因此EuTiO3被称为量子顺电-反铁磁材料。实验研究表明EuTiO3的介电常数在尼尔温度附近出现异常，且加磁场会影响EuTiO3介电性质，加电场会影响它的磁性质，这说明EuTiO3的磁和电的序参量之间存在较强的耦合相互作用，它作为有潜力的单相多铁性材料受到了研究者的广泛关注。Fennie等人[2-4]运用第一性原理的方法计算发现双轴应力可以使EuTiO3由反铁磁顺电体转化为铁磁-铁电体。后来，Lee等人[5]运用实验的方法证实了应力可以使EuTiO3由反铁磁顺电体转化为铁磁-铁电体。Shvartsman等人[6]在EuTiO3中发现了强的E2H2耦合。Morozovska等人[7]运用Landau-Ginzburg-Devonshire(以下简称LGD)理论研究了EuTiO3纳米线的铁电性及铁磁性。

另一方面，自从在传统的铁电材料PbZr0.95Ti0.05TiO3中发现了巨电熵效应和在Cd5Si2Ge2合金中发现了巨磁熵效应，电(磁)熵特性的研究成为材料科学研究者的热点课题。所谓电(磁)熵效应是指改变施加在铁电(磁性)材料上电(磁)场的大小而引起铁电(磁性)材料的变冷或变热[8-11]。常常以由外加电(磁)场的改变而引起的绝热情况下温度的改变(ΔTad)或等温情况下熵的改变(ΔSiso)为特征。具有较大电(磁)熵效应的材料可以广泛应用于芯片等电子器件的制冷、热泵、热电换能器等。目前大部分工作只关注于传统的铁磁体和铁电体。由于多铁性材料中既有磁极化又有电极化，外加电场既改变了电极化又通过磁电耦合效应改变了磁极化，因此多铁性材料中的熵变问题是当前一个热点课题。Ramachandran等人[12]实验报道了用溶胶-凝胶法制备了BiFeO3陶瓷材料，研究了其低温磁熵效应；Balli等人[13]研究了在沿ac平面施加一个相对较小的磁场时，多铁性材料TbMn2O5单晶通过沿b轴旋转可以实现较好的可逆磁熵效应；Vopson[14]运用热力学理论系统地研究了多铁性材料的多熵效应，所谓多熵效应是指在外加电场或磁场作用下，多铁性材料中的绝热可逆温度的改变。这些文献报道说明EuTiO3材料具有较好的磁熵特性。Mo等人[15]通过测量在外加磁场0.01 T时，EuTiO3材料的零场冷却和场冷却下的磁化强度随温度的变化关系，以及等温磁化强度随外加磁场的关系，从而计算了EuTiO3材料的等温熵变和致冷能力，研究表明EuTiO3材料具有较大的可逆磁熵效应。Midya等人[16]采用固态反应法制备了单晶和多晶EuTiO3陶瓷材料，测量了其磁化强度和比热容，研究表明在外加磁场变化7 T时，在相变温度附近绝热温度差可达21 K；同时在低磁场下可以获得较好的磁熵效应。

然而EuTiO3纳米线的电场导致的熵变特性本文将运用LGD理论和热力学理论相结合的方法进行分析研究，旨在寻找获得良好的熵变特性的有效途径。

1 理论模型与分析

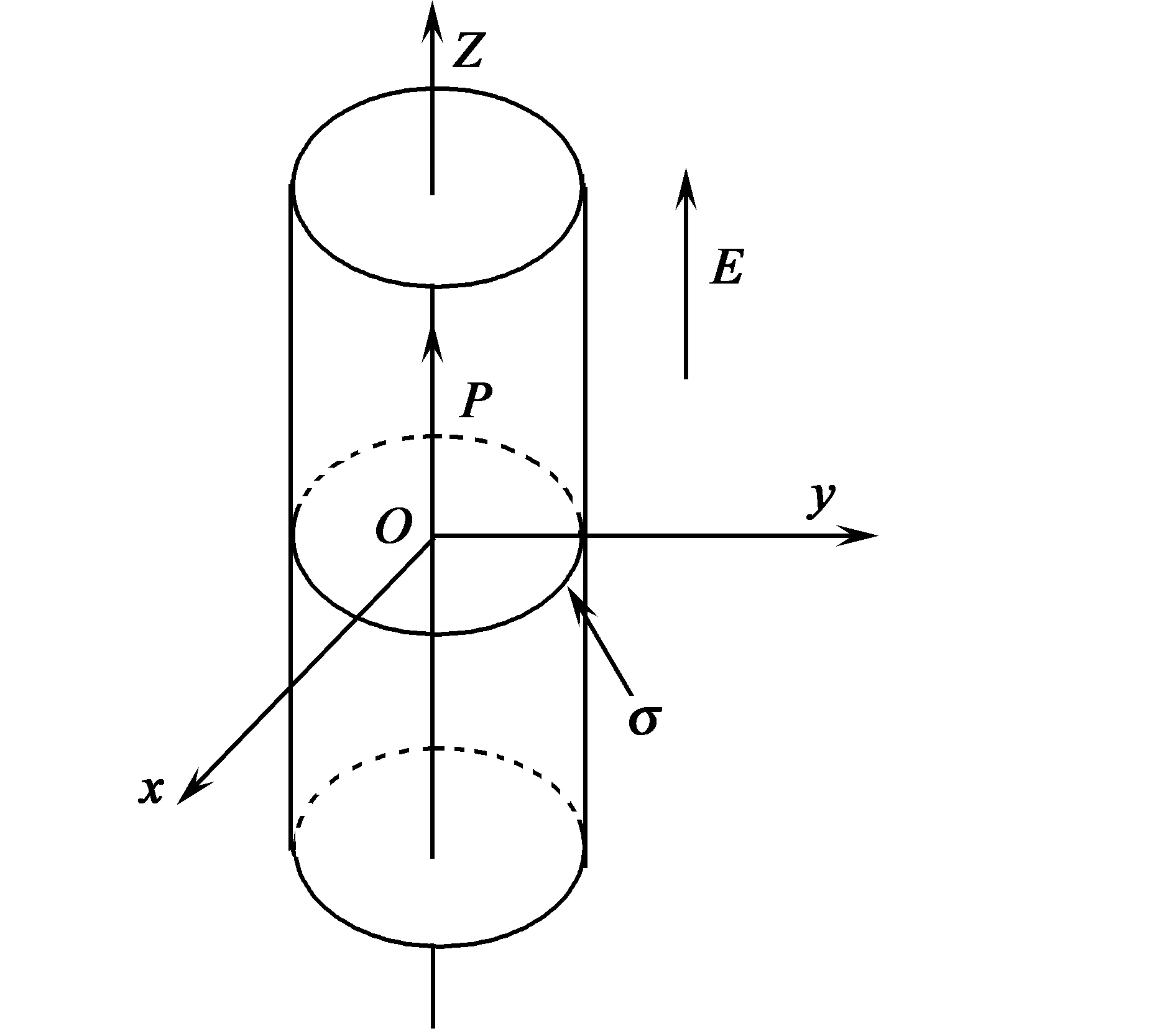
图1 EuTiO3纳米线结构

文献[7]表明EuTiO3纳米线由于内禀表面应力作用而诱导产生铁电性和铁磁性。EuTiO3纳米线结构示意图如图1所示，外加电场沿纳米线轴向方向，电极化矢量P(0，0，P)也沿轴向方向。采用LGD理论来描述EuTiO3纳米线。总自由能G取决于电极化强度矢量P，磁化强度矢量M=(Ma+Mb)/2(a和b对应于两个磁性子格)，及反磁化强度矢量L=(La+Lb)/2，其表达式为

(1)

其中GP，GM，GME分别为电极化、磁化相关的自由能以及双二次磁电耦合能，可分别表示为

(2)

(3)

(4)

为简单起见，本文未考虑表面压电效应和压磁效应，并且只考虑到极化的四次方项，纳米线的总自由能可表示为

(5)

其中朗道修正系数αPR(R,T),αMR(R,T)和αLR(R,T)分别为

(6)

(7)

(8)

另一方面，根据热力学理论，由弹性吉布斯自由能的微分形式[14]

dG=-SdT-MdH-PdE,

(9)

宏观物理量熵、电极化强度以及磁化强度可表示为

(10)

可得麦克斯韦关系式

(11)

熵变效应可以用等温下的熵变和绝热下的温度改变量两个物理量来表征。熵体现了电偶极子随外电(磁)场以及温度的变化情况。其等温下的熵变

(12)

绝热过程由于没有热量的交换，熵是减少的，所以温度必需升高来补偿熵的减小。本文仅研究电场导致的熵变，其绝热温度差的表示如下

(13)

其中CEμ是EuTiO3的单位体积的比热容，χm为磁性极化率，αe满足dM=αe·dE。

2 数值计算结果与讨论

计算中所用的EuTiO3材料的相关唯象参数见参考文献[7]。在不加外电场情况下，文献[7]中给出了温度-表面径向应力相图以及温度-纳米线半径的相图。由图中可知在一定的表面径向应力、一定的半径尺寸下，EuTiO3纳米线可以实现多铁性(铁电-铁磁性，铁电-反铁磁性)、铁电-顺磁性、顺电-反铁磁性。本文为了研究EuTiO3纳米线的电致熵变特性，只关注在外加电场时，高温区的铁电-顺磁相区域以及低温区的铁电-铁磁相区域。

2.1 高温区铁电-顺磁共存区域的熵变特性

高温区的铁电-顺磁共存区域，此时序参量只有电极化强度，不存在磁电耦合现象。图2给出了在给定EuTiO3纳米线半径R=1 nm时，在不同的外加电场和不同的表面张量系数时，极化强度随温度的变化关系。图2(a)—(c)分别对应μ=10，12，15 N/m。由图中可知表面张量系数对EuTiO3纳米线的极化强度有较大的影响。在无外加电场时，在给定表面张量系数μ时，自发极化强度随着温度的升高而逐渐减小，相应的铁电-顺电相的相变温度随着表面张量系数的增加而升高。在给定温度和表面张量系数时，极化强度随着外加电场的增加而有较明显地增大，这使EuTiO3纳米线成为较好的熵变效应材料成为可能。

(a) μ=10 N/m (b) μ=12 N/m (c) μ=15 N/m

图3给出了当给定ΔE=100 kV/cm时，EuTiO3纳米线的绝热温度差ΔT随温度的变化关系。图3(a)是给定表面张量系数μ=15 N/m，对应不同的半径R=0.8,0.9,1.0 nm；图3(b)是给定R=0.8 nm，对应不同的表面张量系数μ=10,12,15 N/m。由图3(a)可知，在较低温度区域，给定温度下绝热温度差随着纳米线的半径增大而增大，而在较高的温区有相反的趋势。给定纳米线半径，在某一温度临界值时，绝热温度差达一峰值。当R=0.8 nm时，可获得较大的绝热温度差ΔT=7.4 K。另外，由图3(b)可以看出，绝热温度差的最大值随着内禀表面张力系数的增大而增大。

(a) μ=15 N/m (b) R=0.8 nm

2.2 低温区铁电-铁磁共存区域的熵变特性

文献[2]报道了在低温区在一定的表面应力作用和一定的半径范围内可以实现铁电-铁磁性。图4是在给定半径R=1 nm时，在低温区磁化强度(图4(a))与极化强度(图4(b))随温度的变化关系。由图中可知，磁化强度和极化强度都随着表面张量系数的增大而增大。由于表面张量系数变大导致的固有表面应力增加，会使相应的极化强度与磁化强度增大，从而铁磁相变温度升高。在低温区由于强的双二次磁电耦合相互作用，极化强度会诱导磁化出现铁磁相，固有表面应力变大时，极化强度也会增大，由于耦合影响，相应的磁化强度也相应增加。应变张量数值对磁化强度影响很大，且相应的铁磁-顺磁相变温度随其增大而提高。由此可知EuTiO3纳米线可能具有多熵效应。图5给出了在低温区0～30 K，EuTiO3纳米线绝热温度差随温度的变化关系。图5(a)和(b)图分别对应于μ=10 N/m，R=0.8,0.9,1.0 nm和R=1.0 nm，μ=10,12,15 N/m。由图中可知，在磁相变温度附近，绝热温度差可以达到一个较大的峰值，且峰值随着纳米线半径的增大和表面张量系数的减小而略有增大。当μ=10 N/m，R=1.0 nm时，可获得较大的绝热温度差ΔT=2.2 K。

(a) 磁化强度 (b) 极化强度

(a) μ=10 N/m (b) R=1.0 nm

3 总 结

本文采用Landau-Ginzburg-Devonshire理论来描述EuTiO3纳米线。总自由能表达式包括电极化强度矢量P、磁化强度矢量M、反磁化强度矢量L。同时根据热力学理论，从弹性吉布斯自由能的微分形式出发，可以推导出电场导致的绝热温度差ΔT表达式。研究结论如下：

(1)在高温铁电-顺磁区域，当ΔE=100 kV/cm，R=0.8 nm时，可获得较大的绝热温度差ΔT=7.4 K。

(2)在低温区0～30 K，在一定的表面径向应力、一定的半径尺寸下，EuTiO3纳米线可以实现铁电-铁磁性。在磁相变温度附近，绝热温度差可以达到一个较大的峰值，且峰值随着纳米线半径的增大和表面张量系数的减小而略有增大。当μ=10 N/m，R=1.0 nm时，可获得较大的绝热温度差ΔT=2.2 K。

因此，通过调节EuTiO3纳米线半径和表面径向应力的大小，可以使EuTiO3纳米线在低温区和高温区都有可能具有良好的熵变特性，特别是使得多铁性材料在低温区实现较好的低温固态制冷成为可能，为实验研究者提供了一个提高多铁性材料熵变特性的有效途径。本文仅讨论了外加电场导致的EuTiO3纳米线熵变特性，在接下来的工作中，我们将系统地研究外加磁场导致的EuTiO3纳米线的多熵效应。

[1] 王克锋，刘俊明，王雨.单相多铁性材料-极化和磁性序参量的耦合与调控[J]科学通报,2008,53(10):1098-1135.

[2] SCHIEMER J,SPALEK L J,SAXENA S S,et al.Magnetic field and in situ stress dependence of elastic behavior in EuTiO3from resonant ultrasound spectroscopy[J].Phys Rev B,2016,93(5):054108-1-18.

[3] SCAGNOLI V,ALLIETA M,WALKER H,et al.EuTiO3magnetic structure studied by neutron powder diffraction and resonant x-ray scattering[J].Phys Rev B,2012,86(9):094432-1-7.

[4] FENNIE C J,RABE K M.Magnetic and Electric Phase Control in Epitaxial EuTiO3from First Principles[J].Phys Rev Lett,2006,97(26):267602-1-4.

[5] LEE J H,FANG L,VLAHOS E,et al.A strong ferroelectric ferromagnet created by means of spin-lattice coupling[J].Nature,2010,466(19):954-958.

[6] SHVARTSMAN V V,BORISOV P,KLEEMANN W.Large off-diagonal magnetoelectric coupling in the quantum paraelectric antiferromagnet EuTiO3[J].Phys Rev B,2010,81(6):064426-1-4.

[7] MOROZOVSKA A N,GLINCHUK M D,BEHERA R K,et al.Ferroelectricity and ferromagnetism in EuTiO3nanowires[J].Phys Rev B,2011,84(20):205403-1-11.

[8] MISCHENKO A S,ZHANG Q,SCOTT J F,et al.Giant Electrocaloric Effect in Thin-Film PbZr0.95Ti0.05O3[J].Science,2006,311(5765):1270-1271.

[9] PECHARSKY V K,GSCHNEIDNER K A.Jr.Giant Magnetocaloric Effect in Gd5(Si2Ge2)[J].Phys Rev Lett,1997,78(23):4494-4497.

[10] GRUNEBOHM A,NISHIMATSU T.Influence of defects on ferroelectric and electrocaloric properties of BaTiO3[J].Phys Rev B,2016,93(13):134101-1-12.

[11] PALACIOS E,TOMASI C,SAEZ-PUCHE R,et al.Effect of Gd polarization on the large magnetocaloric effect of GdCrO4in a broad temperature range[J].Phys Rev B,2016,93(6):064420-1-8.

[12] RAMACHANDRAN B,RAMACHANDRA RAO M S.Low temperature magnetocaloric effect in polycrystalline BiFeO3ceramics[J].Appl Phys Lett,2009,95(14):142505-1-3.

[13] BALLI M,JANDL S,FOURNIER P,et al.Giant rotating magnetocaloric effect at low magnetic fields in multiferroic TbMn2O5single crystals[J].Appl Phys Lett,2016,108(10):102401-1-5.

[14] VOPSON M M.The multicaloric effect in multiferroic materials[J].Sold State Commun,2012,152(23):2067-2070.

[15] MO Z J,SHAN J,LI L,et al.Observation of giant magnetocaloric effect in EuTiO3[J].Mater Lett,2015,158:282-284.

[16] MIDYA A,MANDAL P,RUBI Km,et al.Large adiabatic temperature and magnetic entropy changes in EuTiO3[J].Phys Rev B,2016,93(9):094422-1-7.

[责任编辑：张存凤]

Electrocaloric effect of EuTiO3nanowires

XU Qiu-yan, CAO Hai-xia

(College of Physics, Optoelectronics and Energy, Soochow University,Suzhou 215006, China)

The paper aims to investigate the electrocaloric effect of EuTiO3nanowires based on the Landau-Ginzburg Devonshire theory and thermodynamic theory. Our calculations show that the EuTiO3nanowire exhibits a large adiabatic temperature differenceΔT=7.4 K whileΔE=100 kV/cm,R=0.8 nm in the high-temperature ferroelectric-paramagnetic phase. In addition, it has been found that the ferroelectric- ferromagnetic state of EuTiO3nanowires can be realized under a given surface radial stress and a fixed radius in the low temperature region, which provides an effective means to realize excellent low-temperature electric field-induced caloric effect. The maximum of the adiabatic temperature change near the magnetic phase-transition temperature can be increased slightly with the increase in the radius of nanowire and with the decrease in the surface tension coefficient. A large adiabatic temperature differenceΔT=2.2 K can be obtained whileμ=10 N/m,R=1.0 nm.

EuTiO3nanowire; electrocaloric effect; Landau-Ginzburg-Devonshire theory(LGD)

2016-12-29

2017-01-30

国家自然科学基金资助项目(11104194)；苏州大学研究生高水平《固体物理》课程建设项目资助(58320202)

徐秋艳(1991—)，女，江苏省靖江市人，苏州大学硕士研究生，主要研究方向为凝聚态理论;[通信作者]曹海霞(1971—)，女，江苏省如东县人，苏州大学副教授，博士，主要研究方向为凝聚态理论。

1673-2944(2017)02-0080-07

O469

A