一种面向对缝测量的双线结构光光条中心提取方法*

丁祖娇，李泷杲，翟建军，李 栋

（1.南京航空航天大学机电学院，南京 210016；2.中航工业江西洪都航空工业集团有限责任公司，南昌 330024）

基于线结构光的三维视觉检测技术[1]，由于检测速度快、检测过程与待检表面无接触等优点，在工业中有着广泛的应用前景[2-3]，如GapGun、Gocator已经应用于航空与汽车领域的对缝测量中。这些测量设备均采用单线结构光进行对缝测量，本文采用双线结构光对缝测量系统，能够有效避免在单线结构光对缝测量中对测量姿态的严格要求，提高测量结果的精度和稳定性。由于双线结构光对缝测量依赖的是双结构光与蒙皮对缝边界相交形成的4个特征点，点的提取误差将影响最终的测量结果，而点的提取精度又取决于光条中心的提取精度，因此结构光光条中心提取的是否准确，直接影响到测量结果的精度。

从实现方法上分析，将现有的光条纹中心提取技术归结为两大类[4]：一类是以几何中心作为光条纹中心的提取方法，如阈值法、边缘取中法、骨架细化法等[5-6]，这类方法算法简单，运行速度快，但精度低，受阈值与噪声影响较大。另一类是以能量中心作为光条纹中心的提取方法，如极值法、重心法、Steger法和高斯拟合法等。灰度重心法是将光条宽度范围内横截面上的灰度值重心作为光条的中心，在灰度重心法的基础上，一些研究提出了应用灰度梯度计算光条法线方向，在法线方向上应用灰度重心法来精确提取光条中心的方法[7-10]。该方法有效地弥补了传统重心法不能处理光条法线方向和方向模板法只能获得光条近似法线方向的不足，提取精度较高。Steger[11]利用Hessian矩阵计算条纹的法线方向，把法向的极值点作为光条中心点，具有较高的精度和较好的鲁棒性，但运算量大，实时性差。Lukas等[12]提出了先确定条纹中心的大致位置，然后以该位置附近的5个像素为高斯拟合数据，求取激光条纹的中心位置。该法仅适用直线度较好、粗细均匀的激光条纹。高世一等[13]针对该问题提出了变边限高斯拟合法，由于每一列的拟合数据随着激光条纹宽度变化而变化，提取宽度不同的激光光条效果很好，具有亚像素级的精度和较高的鲁棒性。

由于现在的激光条纹光强已不符合严格意义上的高斯分布，且采用现有的高斯拟合和灰度重心法每次只能求取一根光条的中心位置，本文针对双线结构光所获取的激光条纹截面灰度值分布呈现出一定的周期性，且结构光条纹存在光条粗细不均、曲率变化的情况，在考虑光条法线方向的基础上，提出了一种基于自适应阈值和傅里叶拟合的光条中心提取方法，能够一次完成两根结构光光条中心的精确提取。

1 双线结构光光条截面模型分析

高斯点光束射入圆柱透镜后被展开形成一个连续的光平面，光平面投射到物体表面形成了有一定厚度和亮度的激光条纹。理想情况下，激光条纹光强符合高斯分布。但是，由于被测物本身的材质均匀性、透光性、颜色、形状和表面粗糙度等不同的影响，工件上各处的光强反射率并不相同，在相机观测方向上从被测物表面反射的光带截面光强的分布发生变化，图像上光带截面的灰度分布呈非正态分布，并且针对双线结构光条纹，采用两个相同的激光器，所获取的激光条纹截面灰度值分布呈现出一定的周期性。

图1和图2中的散点是基于自适应阈值在法线方向上获得的某一截面上的灰度值分布图。可知，在远离条纹中心处灰度值很小，进入光条范围内，光条灰度值迅速增大，条纹中心附近的几个像素点处于饱和状态，灰度值相同并且达到极值。对这些灰度值点分别进行高斯拟合和傅里叶拟合，如图1与图2中的实线所示。

由于截面处的灰度值分布有一定周期性，而高斯函数并不是周期性函数，由图1可知，双线结构光条纹的截面上的光强分布并不符合高斯分布，如采用高斯拟合进行光条中心提取，需要对每根光条单独拟合，增加运算量，实时性差。而傅里叶函数是周期性函数，双线结构光条纹截面上的光强分布符合傅里叶拟合（图2）。

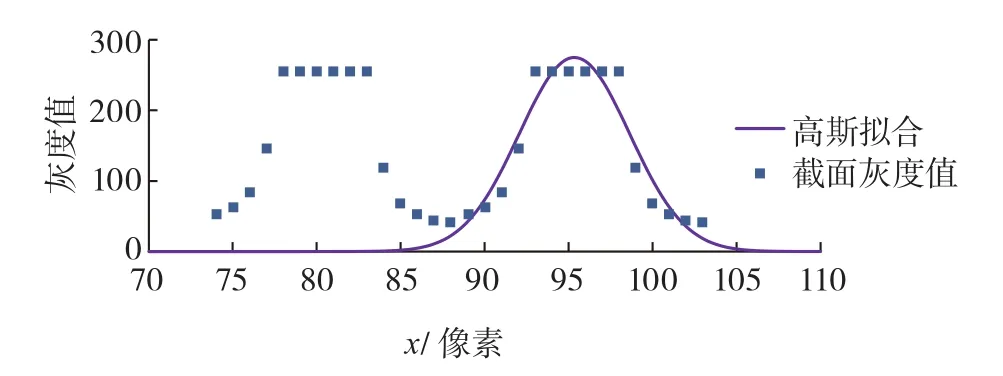
图1 激光条纹截面灰度值分布与高斯拟合Fig.1 Distribution of gray value of laser stripe cross section and Gauss fitting

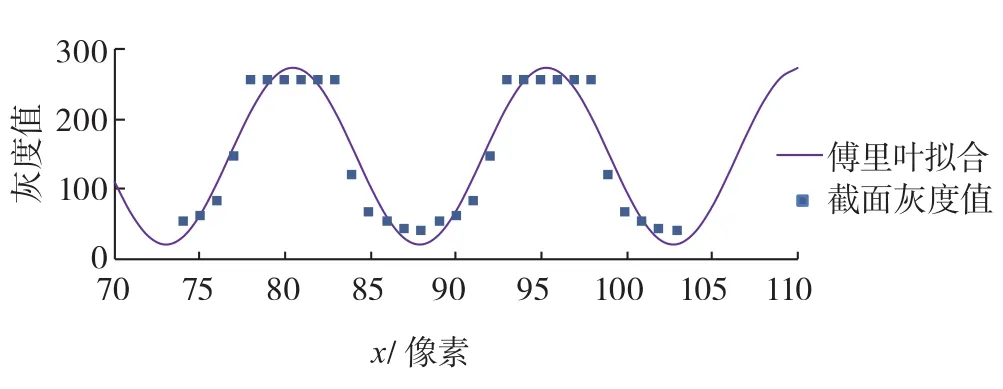
图2 激光条纹截面灰度值分布与傅里叶拟合Fig.2 Distribution of gray value of laser stripe cross section and Fourier fitting

2 基于自适应傅里叶拟合的光条中心提取方法

本文提出的基于自适应阈值和傅里叶拟合的光条中心提取方法主要包括以下4个步骤：

（1）针对光条图像，通过骨架细化的方法获取光条中心的粗略位置，光条中心位置粗略提取的目的就是将图像中结构光光条的骨架提取出来。

（2）在获取的骨架上，由于骨架处的梯度变化较小，不利于光条法向的精确求解，所以采用均方灰度梯度的方法，求取光条骨架的法线方向。

（3）针对光条各处的条纹宽度不均，采用自适应阈值，来确定光条每一个法向截面处光条的宽度。

（4）在采用自适应阈值确定的条纹法向边界内，利用像素点的灰度值数据，在法线方向上基于傅里叶拟合来进行光带中心位置的求取。

2.1 光条中心位置粗略提取

根据光条图像的灰度直方图，选择合适的阈值，对光条图像进行二值化处理，然后分别计算二值图像在水平方向和垂直方向的一维投影矩阵，比较两个一维投影矩阵中非零值的数目来确定光条的走向，拥有较多非零值的一维投影矩阵即为光条的走向。本文中分析光条走向为垂直方向的情况，即在水平方向上求取光条中心的粗略位置。

对二值化的光条图像而言，0为背景，1为目标。针对图像中的任意像素P0，构造它的八邻域如图3所示。图4为P0的左右各两个邻点。先对整个图像逐点作点运算，若该点为背景点数时（即P0=0），则不作任何动作；若该点为光条上的点时（即P0=1），则依据算法判断该点是否应删除，其步骤如下：

（1）若满足如下条件，则标记下该点；

·P0=1

· （Pn-1=0&&Pn+1=1&&Pn+2=2）

（Pn-2=1&&Pn-1=1&&Pn+1=0）

·erasetable[num]=1

（num=P1+2*P2+4*P3+8*P4+16*P5+32*P6+64*P7+128*P8）

（2）逐行遍历整幅图片，删除步骤1中标记的点；

（3）重复步骤1和2直到没有点被删除为止。

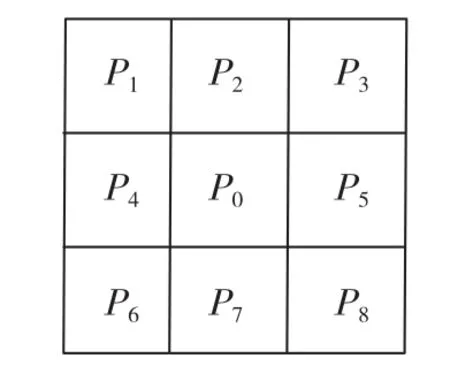
图3 P0的八领域Fig.3 Eight areass of P0

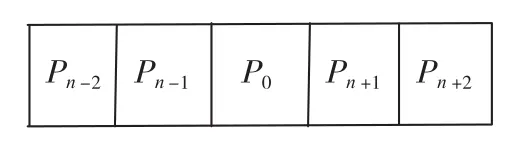
图4 P0的邻点Fig.4 Adjacent points of P0

2.2 光条骨架法线方向求解

设骨架上任意一点（x，y）处的灰度值记为f（x，y），则点（x，y）处的方向角θ（x，y）计算如下：

在复平面上任意向量取平方后，该向量与x轴正方向的夹角将增加一倍，根据这一特质，用复平面上的向量f=（fx，fy）来表示灰度梯度，取其平方得：

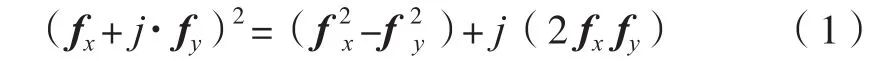
式中，实部为平方灰度梯度的实轴分量，虚部为平方灰度梯度的虚轴分量，fx与fy分别为采用Sobel梯度算子计算点（x，y）在x方向与y方向的偏导数。

为了提高光条骨架法线方向求解的精度，以点（x，y）为中心，取5×5区域内的平方灰度梯度的平均值来计算该点法向，则法向角θ（x，y）计算公式为：

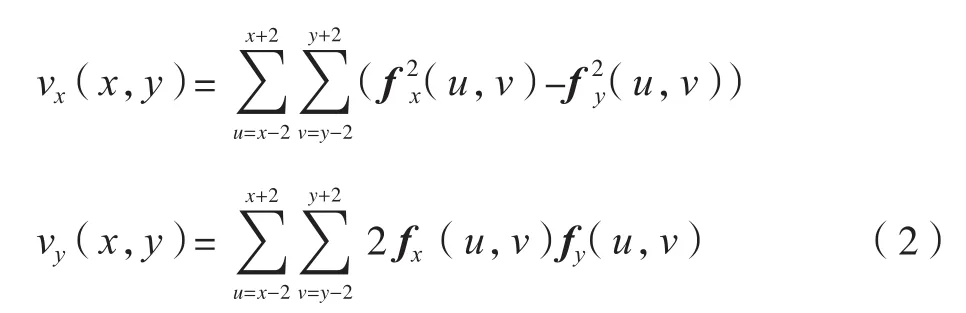
式中，vx（x，y）和vy（x，y）分别为均方灰度梯度向量的实部和虚部，则：

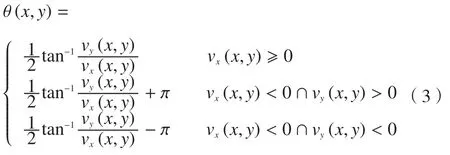
依照上述步骤即可获得骨架上每一点的法线方向。

2.3 自适应阈值法确定条纹法向宽度

线光源激光器距被测物体表面距离的不同，物体表面形状不规则和反射特性不一致，都会引起图像上激光光带宽度的变化。本文测量系统中测量距离在100mm左右，双线激光器采用的是两条平行激光。设图像上光带的粗略宽度范围为两根光条骨架中心之间的距离加上2倍光条宽度nw，光条宽度nw用检测出的光条两个边缘在法线方向上的像素距离来表示，利用Sobel算子[14]来进行光条边缘的检测。

本文中采用Sobel边缘算子在水平方向和竖直方向的两个模板，如图5所示，其中图5（a）中的模板可以检测出光条图像中光条在水平方向的边缘，图5（b）中的模板可以检测出光条图像中光条在垂直方向的边缘，在实际的应用中，把光条图像中的每一个像素都与这两个模板进行卷积运算，取其中的最大值最为光条的边缘输出。

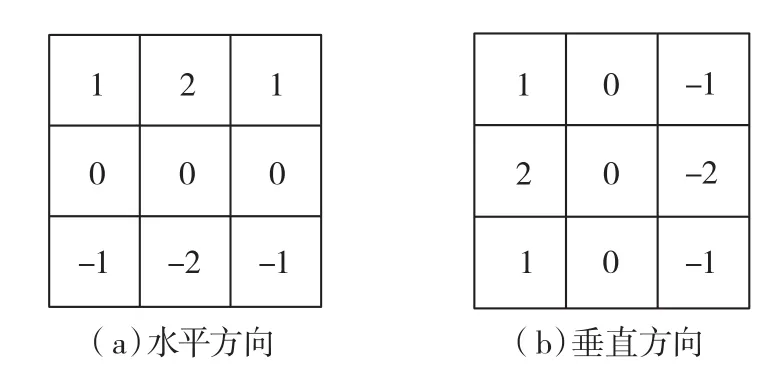
图5 Sobel算子模板Fig.5 Sobel operator template

在获得法线方向上每一处的光条宽度nw后，设第k列的光带中心粗略位置为Ci，Cj，在Ci，Cj处的法线方向上取左右各nw像素之间的范围作为条纹的粗略宽度，如图6所示。在粗略宽度内还还必须再精确地确定光带的边界，以提高后续傅里叶拟合法计算光带中心位置的准确度。具体算法如下：

（1）计算出Ci，Cj处法向上Ci-nw列至Ci+nw列范围内灰度值的平均值IM；

（2）求出Ci-nw列至Ci+nw列范围内灰度值小于IM的像素灰度值的平均值Ih；

（3）把Ih作为光带边界的灰度阈值可以自适应地将光带区域与背景分割开来。

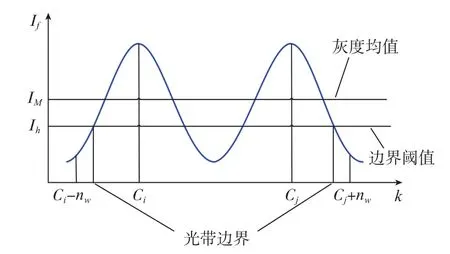
图6 自适应阈值计算条纹法向宽度Fig.6 Normal width of the light stripe by the adaptive threshold method

2.4 傅里叶拟合计算光条中心亚像素坐标

傅里叶函数的数学表达式如下：

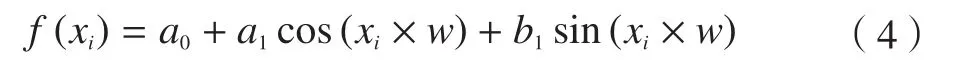
式中，a0、a1、b1是傅里叶函数的参数，w是数据的频率信息。拟合不同的灰度值点会得到相应的参数和频域信息。

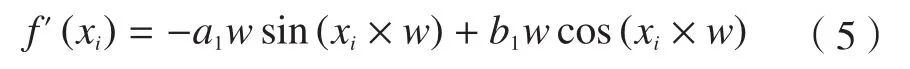
对式（4）左右两边求导得：光条中心位置即为傅里叶拟合曲线的峰值点，在光条法向宽度范围内，令

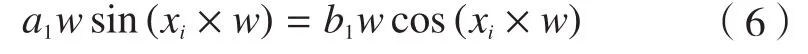
可得光条的中心位置为：

3 试验与分析

图7为双线结构光对缝测量的试验装置图。图像采集相机选择大恒CCD相机F-504B/C，分辨率为2452×2056，镜头选择大恒Computar定焦镜头M0814-MP2，焦距为8mm，激光条纹采用鲍威尔激光器3D扫描测量仪产生，输出的波长为650nm，输出功率可调，最大输出功率为100mW。

图7 试验装置图Fig.7 Experimental device diagram

3.1 双线结构光对缝测量原理

双线结构光对缝测量的模型如图8所示。被测量的缝隙由两组互相垂直的平面构成，如图中的a1、a2、a3、a4平面，a1、a2平面的交线构成了缝隙的左边界，a3、a4平面的交线构成了缝隙的右边界。激光器将激光投射到被测物体表面，如图8所示，激光平面π1与被测物体表面缝隙的左右边界相交于T1、T4两点，激光平面π2与被测物体表面缝隙的左右边界相交于T2、T3两点。

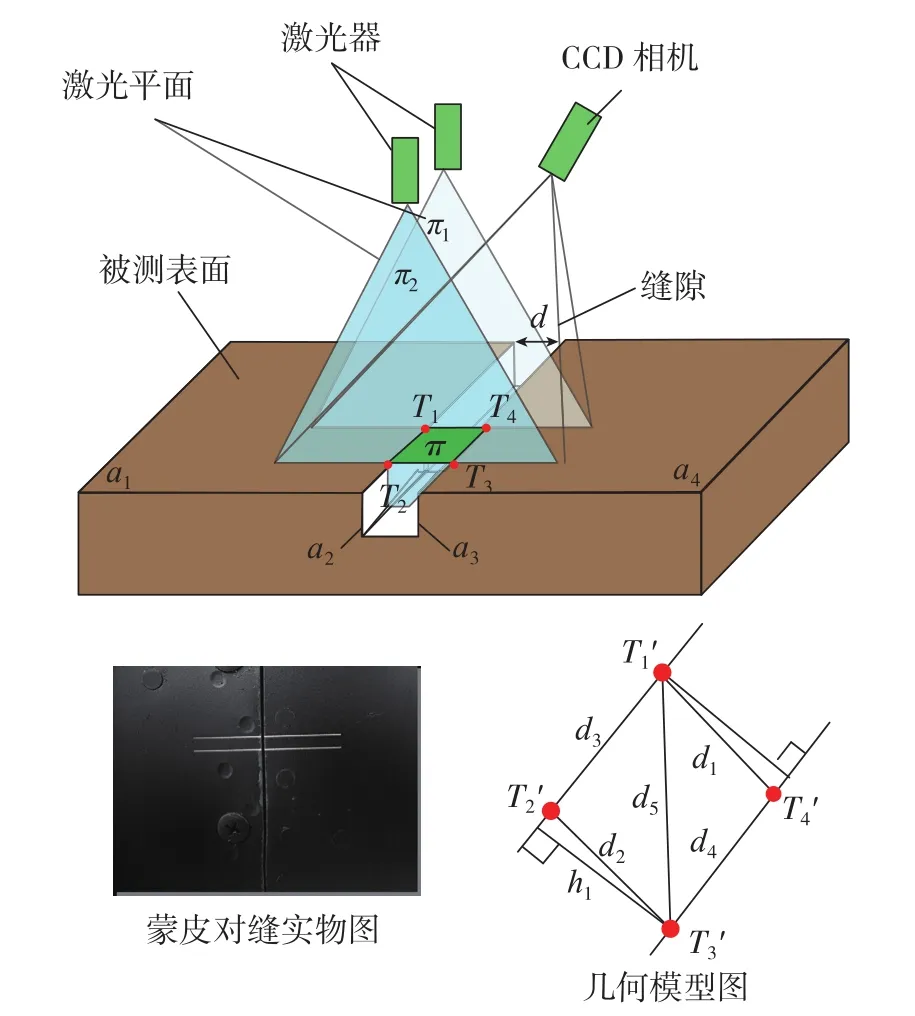
图8 双线结构光对缝测量模型图Fig.8 Diagram of dual linear structured light measurement model

由图8中的几何模型图可知，对于对缝某一位置间隙的测量可以转换成求解该位置附近4个光条特征点形成的四边形高的问题，具体的计算步骤如下：

（1）激光器将双线结构光平面投射到被测物体表面，得到被目标表面调制后的图像；

（2）提取左右边界上的特征点T1、T2、T3、T4；

（3）利用T1、T2、T3、T4这 4 个特征点基于最小二乘法拟合特征平面π；

（4）分别求取特征点T1、T2、T3、T4在特征平面π上的投影点T1'、T2'、T3'、T4'；

（5）分别计算每两个特征投影点间的距离，分别记为d1、d2、d3、d4、d5；

（6）根据式（8）可以求得h1，同理可求得h2；

（7）则由式（9）可以计算出对缝宽度d。

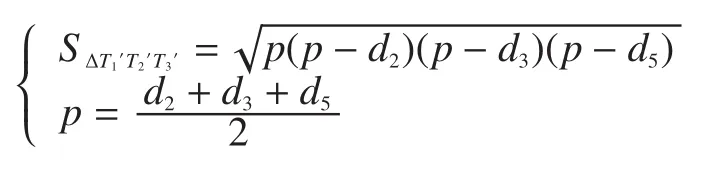
3.2 光条中心提取精度评价

为了验证本文方法的细化精度，设计表面粗糙度为5μm的模拟件，如图9所示。激光器将激光投射到模拟件表面，CCD相机采集激光条纹。

把采集到的激光条纹图像进行感兴趣区域分割，处理后的像素值为250×270，图10（a）是感兴趣区域分割后的光条图像。图 10 中的（b）、（c）、（d）图分别为采取骨架细化法、自适应高斯拟合和自适应傅里叶拟得到的图10（a）的中心线图像，图像输出时对中心的亚像素坐标进行了圆整。

表1为采用骨架细化法、自适应高斯拟合、自适应傅里叶拟合分别提取图10（a）中条纹的中心位置获得的数据。通过拟合条纹中心的直线方程，对比中心点到拟合直线的平均距离，该值越小，表示各个点偏离拟合直线越小，则光条中心提取的精度越高。

表1为采用3种细化方法提取模拟件上激光条纹中心拟合得到的直线方程和提取的光条中心点到拟合直线距离的平均值。由表1可得，采用自适应傅里叶拟合获得的光条中心点到拟合直线的平均距离分别为0.1182个像素和0.1428个像素，优于骨架细化法和自适应高斯拟合，说明本文提出的自适应傅里叶拟合较其他两种方法有较高的可信度，获得的激光条纹中心的精度更高。

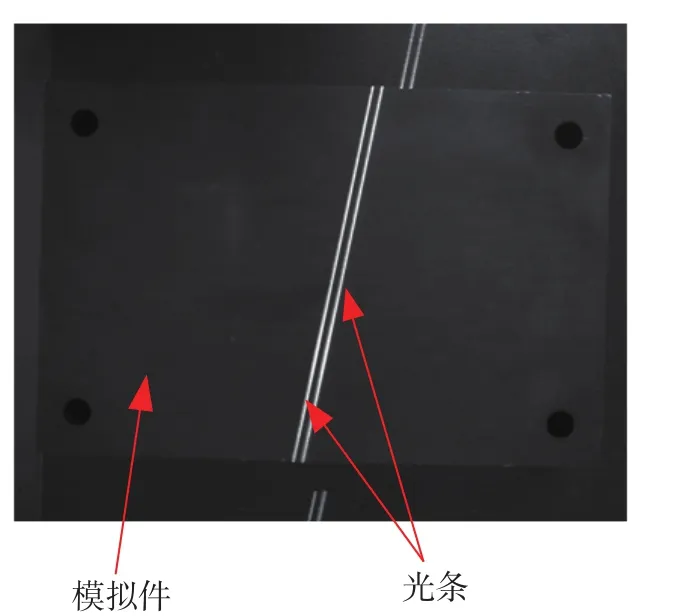
图9 模拟件Fig.9 Simulation part

图10 光条中心提取图像Fig.10 Light stripe center extraction image

3.3 对缝测量精度评价

为验证本文提出的细化方法的测量精度，设计对缝宽度为5mm，加工精度为±0.005mm的试验件（图11）。

图11 对缝试验件Fig.11 Seam experiment part

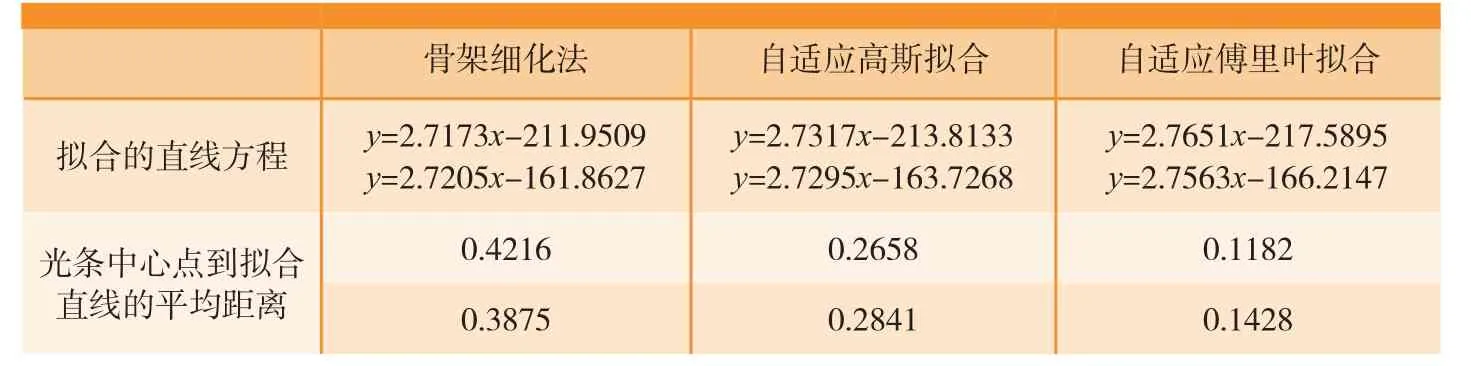
表1 3种方法提取条纹中心对比试验结果表

在保证测量系统其他因素不变的情况下，利用骨架提取法、高斯拟合法和本文所提出的算法分别对这个对缝进行50次测量，图12～14为以这3种细化方法所获得的对缝测量值曲线，从3个对比图中可以明显看出，采用本文所提出的算法获得的对缝测量值波动最小，测量结果精度最高。

表2为试验测量结果比较，可以看出，采用本文所提出的自适应傅里叶拟合法测量对缝，所获得的对缝测量值的精度最高，整个系统的测量误差能稳定在0.04mm以内，具有更好的稳定性。

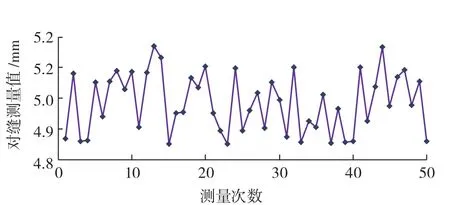
图12 骨架细化法测量数据Fig.12 Measurement data of skeleton thinning method

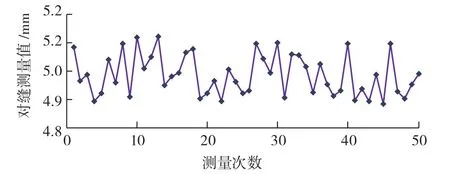
图13 自适应高斯拟合测量数据Fig.13 Measurement data of adaptive Gauss fitting method

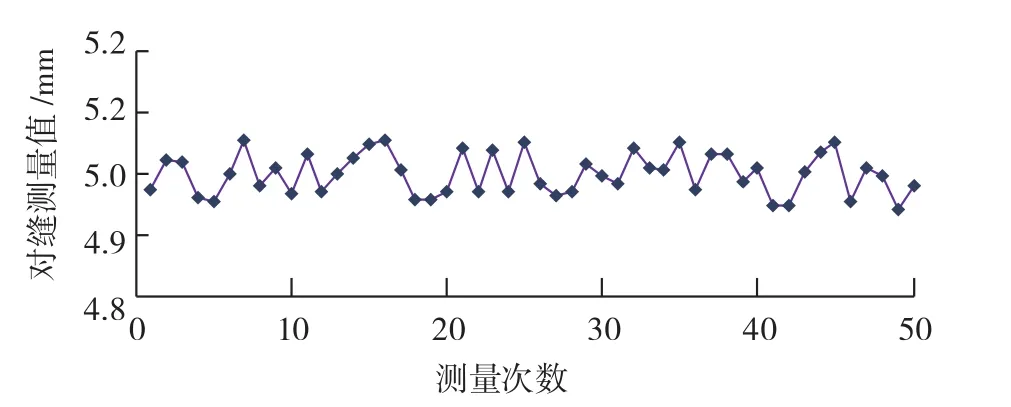
图14 自适应傅里叶拟合测量数据Fig.14 Measurement data of adaptive Fourier fitting method

表2 3种方法提取条纹中心平均误差对比试验结果表 mm

4 结束语

本文根据双线结构光光带截面灰度近似周期性分布的特点，提出一种基于自适应阈值和傅里叶拟合的光条中心亚像素提取方法。该方法采用骨架细化法获得光条中心的粗略位置，采用自适应阈值法提取出条纹各列法向宽度值，运用傅里叶拟合进行光带中心位置的精确计算，具有较高的光带中心提取精度。同时该方法在光条灰度和宽度不均匀的情况下，也能准确地提取出光条的中心位置，提高了对缝测量精度。

参 考 文 献

[1]吴志伟.产生宽测量区域低发散度栅型结构光的光学系统[J].光学学报 , 2013,33(9)： 108-113.WU Zhiwei. Optical system generating wide measurement area and low divergence degree grating structure light [J]. Acta Optica Sinica,2013,33(9)： 108-113.

[2]张广军,田叙.结构光三维视觉及其在工业中的应用[J].北京航空航天大学学报,1996,22(6)：650-654.ZHANG Guangjun, TIAN Xu. Structured light 3D vision and its industry application[J]. Journal of Beijing University of Aeronautics and Astronautics, 1996,22(6)：650-654.

[3]张广军，刘震，魏振忠，等.基于线结构光的四通道舵偏角同步动态测量系统[J].仪器仪表学报，2010, 31(8)：1910-1915.ZHANG Guangjun , LIU Zhen, WEI Zhenzhong, et al. Fourchannel synchronous dynamic measurement system for rudder angles based on line structured light [J]. Chinese Journal of Scientific Instrument,2010,31(8)：1910-1915.

[4]杨建华,杨雪荣,成思源,等.线结构光三维视觉测量中光条纹中心提取综述[J].广东工业大学学报, 2014(1)： 74-78.YANG Jianhua, YANG Xuerong, CHENG Siyuan, et al. Review of extracting the centers of linear structured light stripes for 3D visual measurements[J]. Journal of Guangdong University of Technology,2014(1)：74-78.

[5]崔希军，杨川，刘保华，等.线性结构光心的自适应迭代提取法[J].西安交通大学学报，2007,41(1)：73-76.CUI Xijun, YANG Chuan, LIU Baohua, et al. Self-adaptive iterative method of extracting center of linear-structured light stripe[J]. Journal of Xi’an Jiaotong University, 2007,41(1)：73-76.

[6]JANG J H，HONG K S. Detection of curvilinear structures and reconstruction of their regions in gray-scale images[J]. Pattern Recognition，2002,35(4)：807-824.

[7]熊会元，宗志坚，陈承鹤.线结构光条纹中心的全分辨率精确提取[J].光学精密工程，2009, 17(5)：1057-1062.XIONG Huiyuan, ZONG Zhijian, CHEN Chenghe. Accurately extracting full resolution centers of structured light stripe[J]. Optics and Precision Engineering, 2009,17(5)：1057-1062.

[8]POPOVIC M B， BANDUR V M， RAICEVIC M A，et al.Different methods for fingerprint image orientation estimation[J]. IEEE,http：//paperuri：(3edac5aaf9b2a42adb5384bcec016696) 2012.

[9]LÜ Z H, ZHANG Z Y. Build 3D scanner system based on binocular stereo vision[J]. Journal of Computers, 2012,7(2)： 399-404.

[10]王伟华，孙军华，刘震，等.钢轨磨耗动态测量结构光条纹中心提取算法[J].激光与红外，2010, 40(1)：87-90.WANG Weihua, SUN Junhua, LIU Zhen, et al. Stripe center extrication algorithm for structured-light in rail wear dynamic measurement[J]. Laser & Infrared, 2010,40(1)：87-90.

[11]STEGER C. An unbiased defector of curvilinear structures[J].IEEE，1998,20(2)：113-125.

[12]LUKAS J，FRIDRICH J，GOLJAN M. Detecting digital image forgeries using sensor pattern noise[J]. Electronic Imaging, 2006, 60(72)：362-372.

[13]高世一，杨凯珍.变边限高斯拟合提取激光条纹中心线方法的研究[J].仪器仪表学报,2011,32(5)：1132-1137.GAO Shiyi, YANG Kaizhen. Research on central position extraction of laser stripe based on varied-boundary Gaussian fitting[J]. Chinese Journal of Scientific Instrument, 2011,32(5)：1132-1137.

[14]袁春兰, 熊宗龙, 周雪花,等. 基于Sobel算子的图像边缘检测研究[J]. 激光与红外, 2009, 39(1)：85-87.

YUAN Chunlan, XIONG Zonglong, ZHOU Xuehua, et al. Study of infrared image edge detection based on Sobel operator[J]. Laser & Infrared,2009, 39(1)：85-87.