基于改进免疫算法的可拆卸设计的产品模块划分方法*

魏 巍，彭关伟，吉 军，于 勇

（1.北京航空航天大学机械工程及自动化学院，北京 100191;2. 西安现代控制技术研究所，西安710111;3.中国兵器工业信息中心，北京 100089）

大规模定制（Mass Customization，MC）作为当前信息化时代制造业中最为高效和绿色的生产方式，不仅满足了用户对产品个性化的追求，同时也实现了产品成本的有效控制[1]。随着可持续经济的发展，人们对产品的要求不仅个性化，同时还需考虑产品对环境的影响，这也使得未来企业之间的市场竞争从个性化逐渐扩展成为整个产品生命周期的竞争。模块化设计作为大规模定制中最重要的设计方式，聚合了产品的关键特性，形成了一个具有特定功能的子系统，将不同的子系统进行组合配置，就可以形成具有一定功能的父级系统，根据组合不同就可以产生多种功能相似但是性能、价格等不同系列的产品。绿色设计是在不影响产品基本功能的前提下，将产品的设计扩展到产品生产、制造、使用、维修、报废、回收等全生命周期，减少产品生产使用对环境造成的负担，优化产品给企业带来的利益，尽可能提升资源利用率，间接提升产品的市场竞争力。如果将绿色设计思想与模块化设计方法结合起来，可以同时满足产品的功能属性和环境属性，一方面可以借助模块化设计搭建产品平台，从而快速地从产品平台衍生出多种多样的产品，积极响应客户的需求，大大缩短产品研发与更新周期；另一方面，基于绿色设计思想，产品可以减少或消除对环境的不利影响，方便重用、升级、维修和产品废弃后的拆卸、回收和处理。而在产品的整个生命周期中，产品的可拆卸性对提高资源使用效率，减少环境污染起着关键作用[2]。因此，面向可拆卸设计的模块化方法，是解决绿色大规模可定制问题的关键方法。

目前，国内外学者对可拆卸设计模块划分进行了研究。唐涛等[3]首先将绿色设计思想与模块化设计方法结合起来，并且引入层次分析法，最后提出了绿色模块化设计方法与设计流程。GU等[4]指出了与设计目标相关的生命周期因素，并提出了面向产品全生命周期的集成模块化设计方法。江吉彬等[5]提出了面向对象的层次网络图拆卸模型，并基于该模型对拆卸顺序规划、拆卸路径推理和拆卸性能评价等进行了讨论，最后给出了实用的可拆卸性再设计策略。郭伟祥等[6]提出了一种基于模块化思想的拆卸序列生成方法，并立了模块化产品拆卸模型。魏巍[7]提出了基于环境生态因子的模块划分方法，将产品设计中对环境的影响因素融入到了模块划分当中。

产品的可拆卸属性往往很难量化，而且现有的模块划分方法很难适用于可拆卸设计，因此本文综合了模块化设计方法和可拆卸设计的思想，提出了可拆卸设计的模块化准则，将可拆卸属性进行量化，以可拆卸度、内部聚合度、外部耦合度为优化目标进行模块划分。利用免疫克隆算法进行模块划分，得到模块划分的优化结果，该方法是以模块划分为主要目标，同时兼顾模块零部件之间可拆卸性的复杂程度，最后以某型号飞机前起落架为例说明该方法的可行性和适用性。

1 面向可拆卸性的产品模块化模型

1.1 面向可拆卸设计的概念

可拆卸性设计[8]（Design for Disassembly）是一种绿色设计方法，以提高产品拆卸性能为目的，将传统设计扩展到包括维修、回收等产品生命阶段的产品全生命周期设计，在产品概念设计和详细设计阶段就考虑产品的拆卸问题，用可拆卸性来约束结构设计，使得产品更易拆卸、回收和重用，并将它作为产品设计的一个重要准则。根据不同的拆卸目标，可拆卸性设计可以分为两类：一类是面向产品回收（Design for Recycling）的可拆卸性设计，面向产品回收的可拆卸设计主要考虑产品报废时，将可重用零件或具有回收价值的材料进行回收与利用，将材料进行分类处理，把其中一些有害的材料通过合理的方式处理掉，减少对环境的负面影响；另一类是面向产品维修（Design for Maintenance）的可拆卸性设计，主要是在产品的正常使用期间内，使得产品容易拆装，零部件便于维护。

1.2 可拆卸设计模块化准则

产品的模块化设计是基于对产品功能和结构分析基础之上对产品进行模块划分的，因此产品结构的模块划分对产品的功能结构和可拆卸性程度具有直接影响，产品能否实现可拆卸属性和功能属性的综合协调与模块化准则密切相关。依据可拆卸准则要点，结合模块化设计思想，提出了面向可拆卸设计的模块化准则[9]：

（1）材料相容性准则。

当产品进入废弃回收的生命阶段时，为了能以较低的回收成本高效的回收部分产品零部件，可以在产品模块划分时，将材料相同或者是相似的零部件尽可能划分成为同一个模块。如果模块组成材料兼容性能较好，可以直接将模块作为整体进入回收工艺过程，就可以省去模块的拆卸工序，不仅降低了拆解回收的难度，同时也使回收成本得以控制。

对任意零件i与j，对准则1的零件材料相容相关性因子定义如下：

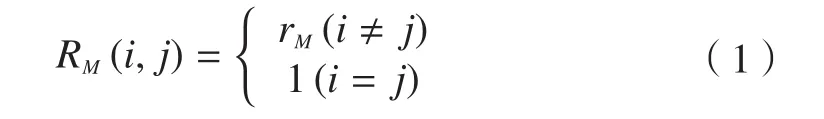
式中，rM为零件i与零件j的材料相容性值。

（2）经济性准则。

产品设计阶段，如果将回收价值相近的零部件划分到同一模块当中，在产品回收时，可对整个产品所有模块进行综合回收价值评估，从而有选择地回收价值较高的模块，回收价值低的模块可以直接利用填埋，焚烧和分解等处理方式处理，可以避免模块的拆卸工作，降低回收成本，提高回收效率。

对任意零件i与j，对准则2的经济性因子定义为：

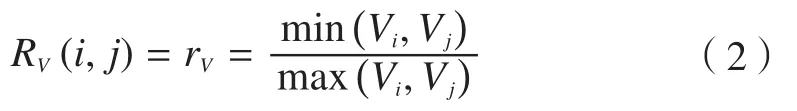
式中，rV为零件i与零件j的回收价值比较关系；Vi、Vj表示零件的回收价值。

（3）回收生态指数准则。

产品中的每个零部件或多或少会对环境造成一定的影响，为了将这种影响降到最低，在产品设计阶段，就对每个零件进行环境生态指数评估，将评估的结果作为设计的参照条件，将指数相似的零件小幅度调整划分成为同一模块，在产品回收时，根据模块的整体环境生态指数来选择处理方式，回收环境生态指数相对较高的模块，采用统一方式整体处理环境生态指数较低的模块，避免了模块的进一步拆解工作，减轻环境的影响。

对任意零件i与j，对准则3的环境生态指数定义为：

式中，rE为零件i与零件j的回收生态指数比较关系；EIi、EIj表示零件i与零件j的回收生态指数。

（4）拆卸性准则。

产品的拆卸复杂度取决于产品中各零部件之间的连接方式分离的难易程度和连接方式种类。因此产品设计时，应保证产品各模块尽可能地采用标准、统一、易于拆卸的接口，例如采用公制的螺栓，尽量不采用焊接、胶接等连接方式；模块内零部件的连接也尽量采用卡扣、限位等连接方式，减少拆卸工具的种类，降低拆卸难度，提高产品可维修性能。

对任意零件i与j，对准则4的拆卸性因子定义如下：

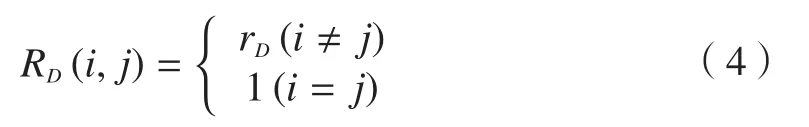
式中，rD为零件i与零件j的拆卸难度。

（5）末端处理方式准则。

报废产品的零部件处理方式一般分为回收、废弃和再制造3种。回收可以根据回收方式不同分为材料回收和能量回收，材料回收一般采用机械方式对材料进行处理，例如轮胎橡胶的回收通常利用磨碎机将橡胶磨成颗粒，然后回收；能量回收是指通过焚烧的方式提取出材料中的能量。再制造一般是将零件拆解、清洗，然后通过二次加工方法修复零件，不同的处理方式工序千差万别。因此，在模块划分时，将具有相同处理方式的零件划到同一模块，可以减少产品回收时的处理难度。

对任意零件i与j，对准则1 的零件末端处理方式相关性因子定义如下：

综合以上5条可拆卸设计模块化准则，依据可拆卸属性相关定义，对任意两个零部件可拆卸属性进行量化评价，从而得到了可拆卸设计的属性值：

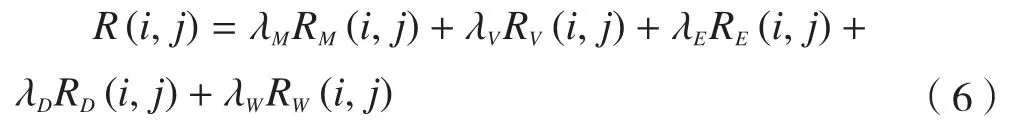
式中，λM、λV、λE、λD、λW分别为对应准则的权重因子，不同设计可根据具体需求赋予不同的权重因子。

2 面向配置的模块划分优化算法

2.1 模块划分的优化目标

2.1.1 可拆卸性

拆卸性的计算[10]是以各个零件之间的可拆卸难度（材料相容性、拆卸经济性、生态保护性、拆卸性和处理方式）为基础的，通过调整零部件的归属的模块，从而使得整个产品的可拆卸度最大，拆卸难度最小。令产品包含零部件的总数为N，模块单元数为M，第i簇模块单元Mi内包含的零部件数为Ni，i=1，2，…，M。通过上述的可拆卸设计模块化准则，根据公式计算出相应的准则值，然后由专家给出各个评价指标的权重值，即可建立模块簇内零部件的相对拆卸度矩阵。

（1）构建模块簇内零部件的相对拆卸度矩阵。

式中为模块Mi内第p个零部件与模块Mj内第q个零部件之间的综合拆卸性。

（2）构建模块簇间综合相对拆卸度数学优化模型模块Mi与模块Mj的相对可拆卸度为：

则模块簇间的综合相对可拆卸度为：

式中为模块簇Mi与模块簇Mj的相对可拆卸度；R为模块簇间的综合相对可拆卸度。

2.1.2 外部独立性

外部独立性是模块划分中最为重要的指标，通常模块独立性是以零部件之间功能、结构为指标进行综合评价的，通过建立零部件关联矩阵反映模块的外部独立性。

（1）构建模块簇内零部件的相对耦合度矩阵：

式中为模块Mi内第p个零部件与模块Mj内第q个零部件之间的综合关联度。

（2）构建模块簇间综合相对耦合度数学优化模型模块Mi与模块Mj的相对耦合度为：

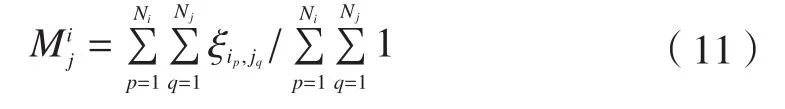
则模块簇间的综合相对耦合度为：

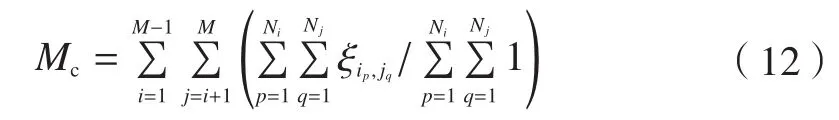
式中为模块簇Mi与模块簇Mj的相对耦合度；Mc为模块簇间的综合相对耦合度。

2.1.3 内部聚合度

内部聚合度是反映同一模块中零部件之间关系紧密的重要指标，模块划分时，通常将内部耦合度作为模块划分的准则之一，内部聚合度可以通过零件综合关联矩阵反映。根据式（10）的关联矩阵M，则第i簇模块的聚合指数为：

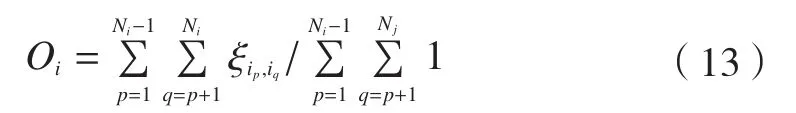
产品中所有模块内部的综合聚合度为：

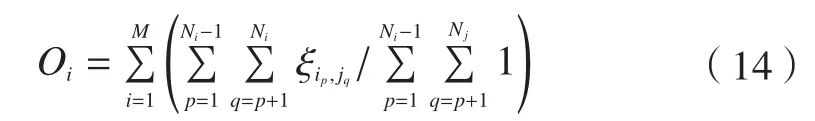
式中，Ni为第i簇模块单元内包含的零部件数为模块簇Mi内部第p个零部件与第q个零部件之间的综合关联度。

2.2 基于免疫克隆多目标优化算法的模块划分

模块划分时，既考虑可拆卸性同时又考虑内部聚合度以及外部独立性，属于多目标优化问题。对多目标规划模型的求解属于典型的有约束多目标优化问题。其数学描述为：

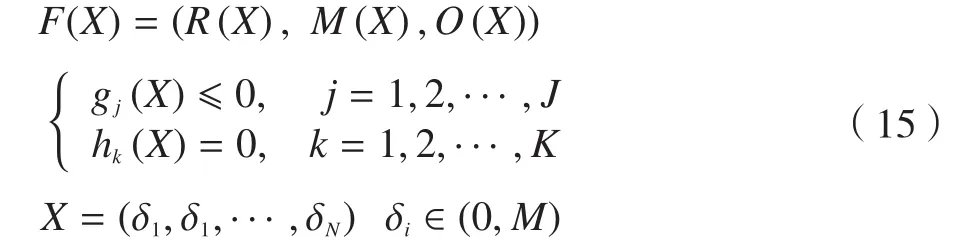
式中，M（X）为极小化目标函数；R（X）、O（X）为极大化目标函数；gj（X）为优化问题的不等式约束；hk（X）为优化问题的等式约束；j与k分别为不等式和等式约束的个数。

本文针对此问题，改进了一种免疫克隆多目标优化算法（A Novel Immune Clonal Algorithm, NICA-Ⅱ）对产品进行模块划分。免疫克隆多目标优化算法由于具有较强的全局搜索能力和较优的局部寻优的能力，可应用于大部分多目标优化当中，但是在模块划分时仍然具有一定的不足和缺陷，因此本文针对模块化划分问题对免疫克隆多目标优化算法[11]进行了改进。模块划分的NICA-Ⅱ过程人工免疫系统[12]主要是借鉴生物免疫系统的信息处理机制发展新的算法，从而为复杂的问题的解决提供新思路。图1所示为用于求解多目标优化的模块划分问题的NICA-Ⅱ流程图。

步骤1：对模块元抗体群进行初始化A（0）={a1（0），a2（0）， …，aN（0）}；给出算法基本参数，最大迭代数G，抗体群规模N，克隆规模M以及初始代数i=0。

步骤2：对模块元抗体群A（i）实施免疫模块克隆操作A（1）（i）=RC（A（i）），实现模块空间的扩张。

步骤3：对模块元抗体群A（1）（i）以概率p实施模块免疫基因操作A（2）（i）=RG（A（1）（i）），完成模块的交叉变异。

步骤4：对模块元抗体群A（2）（i）实施模块克隆选择操作A（3）（i）=RS（A（2）（i）），筛选出满足环境资源条件的模块。

步骤5：对模块元抗体群A（3）（i）实施抗体群更新操作，得到新的抗体群A（4）（i）=RRS（A（3）（i））和新目标函数值矩阵F（A（4）（i））。

步骤6：如果i＞G，则输出模块元抗体群A（i）及其目标函数矩阵F（A（i））；否则，令A（i+1）=A（4）（i），F（A（i+1））=F（A（4）（i）），i=i+1，返回步骤2。

图1 NICA-Ⅱ流程图Fig.1 Flow chart of NICA-II

免疫克隆多目标优化算法的克隆操作是算法实现全局搜索的基础，基因操作以变异操作为主。本算法采用4位二进制数的抗体编码形式，因此变异内容是以概率p对抗体某基因位的基因值取反操作，即跟踪变异二进制基因对的变化。如飞机起落架20个零部件，其中5号部件编码为“0011”，表示其所在的一个划分模块；当以p=0.2的概率经过克隆变异操作后，其划分模块结果为“0010”，如图2所示。

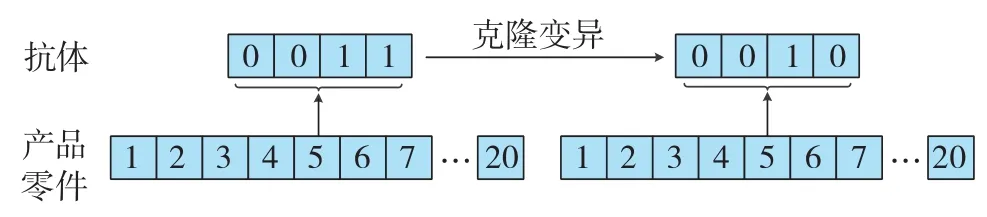
图2 产品零件的抗体二进制编码与克隆变异Fig.2 Antibody of binary encoding and the clone variation of product parts

模块克隆选择操作是将非支配抗体从抗体群中选出，加快收敛速度。模块元抗体群更新操作通过删除非支配抗体中较为拥挤的抗体，保证所得Pareto最优解分布的均匀性。

3 实例验证

起落架是飞机用于地面（或水面）移动的附件装置且唯一支撑整架飞机的部件，起落架是一个集成机械系统、液压系统、电力系统的大型复杂系统，因此它是飞机不可或缺的一部分。图3是某型号飞行器的起落架结构图，表1为起落架简化后的主要零部件。

飞机起落架上主要零部件由上表所示，首先根据上文提出的5种可拆卸准则，分别计算出起落架中任意两个零部件的各准则数值，然后由专家一致协商，认为飞机起落架的拆卸难点主要在于经济型以及拆卸难易度，给出各准则之间的权重指数：λ={0.07，0.31，0.09，0.48，0.05}，经过计算得出零部件之间的相对拆卸度矩阵如下表所示：

图3 某型号飞机前起落架Fig.3 An aircraft landing gear

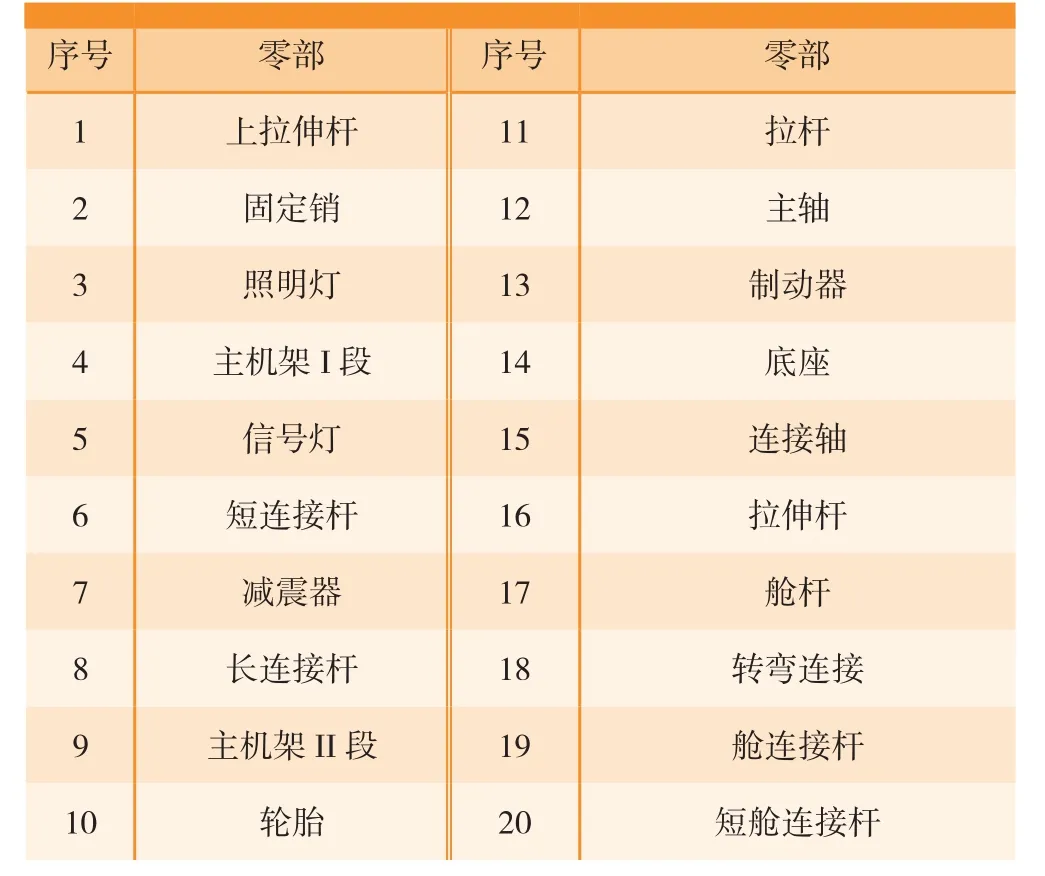
表1 主要零部件

K1 K2 K3 K4 ... K17 K18 K19 K20 K1 1.000 0.504 0.214 0.546 ...0.588 0.822 0.768 0.612 K2 0.504 1.000 0.686 0.384 ...0.366 0.534 0.310 0.558 K3 0.214 0.686 1.000 0.776 ... 0.526 0.486 0.482 0.754 K4 0.546 0.384 0.776 1.000 ... 0.792 0.354 0.218 0.158............... ...............K17 0.588 0.366 0.526 0.792 ... 1.000 0.602 0.746 0.232 K18 0.822 0.534 0.486 0.354 ...0.602 1.000 0.532 0.351 K19 0.768 0.310 0.482 0.218 ...0.746 0.532 1.000 0.114 K20 0.612 0.558 0.754 0.158 ...0.232 0.351 0.114 1.000

各模块根据式（10）计算零部件之间的综合关联度，建立起落架各零部件的相对耦合度矩阵，根据式（7）计算零部件之间综合可拆卸度，建立起落架各零部件的相对可拆卸属性矩阵，归一化处理之后的结果：

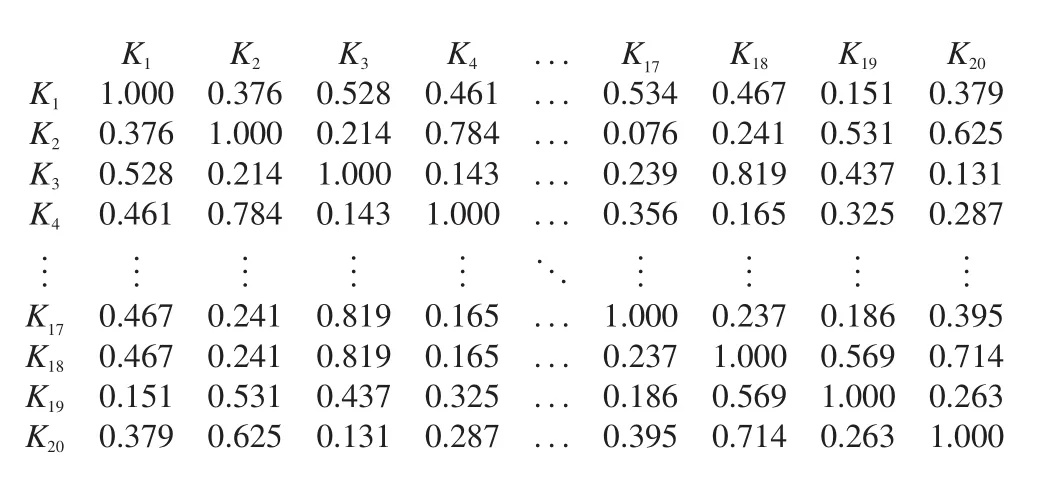
K1 K2 K3 K4 ... K17 K18 K19 K20 K1 1.000 0.376 0.528 0.461 ... 0.534 0.467 0.151 0.379 K2 0.376 1.000 0.214 0.784 ...0.076 0.241 0.531 0.625 K3 0.528 0.214 1.000 0.143 ...0.239 0.819 0.437 0.131 K4 0.461 0.784 0.143 1.000 ...0.356 0.165 0.325 0.287............... ...............K17 0.467 0.241 0.819 0.165 ... 1.000 0.237 0.186 0.395 K18 0.467 0.241 0.819 0.165 ... 0.237 1.000 0.569 0.714 K19 0.151 0.531 0.437 0.325 ... 0.186 0.569 1.000 0.263 K20 0.379 0.625 0.131 0.287 ... 0.395 0.714 0.263 1.000

建立起落架多目标优化数学模型，其目标函数为：

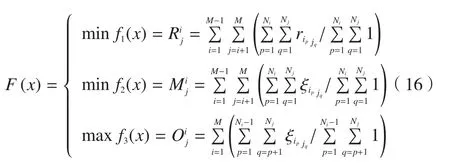
由于模块划分时，模块数量为零件总数的平方根时，模块划分结果最优，因此本文设定模块数量为零件总数N的平方根，约束条件为：

式中，N代表零件的总数，i和j代表模块划分中任意两个模块。

以δi为优化对象，以起落架模块间耦合度最小，模块内部聚合度、稳定性最大为目标函数，进行产品模块划分的多目标优化。编码方式采用二进制编码，初始迭代次数i=0，随机产生规模为100的抗体群：A（i）={a1（i），a2（i）， …，a100（i）}，i表示当前代数，最大代数T=200，克隆比例R=4，变异概率取为p=0.2。计算最终求得的Pareto解集如图4所示。

图4为在相同前提下，分别利用NICA-Ⅱ算法和NSGA算法对该模块划分优化问题进行求解得到的Pareto解集，可以看出NICA-Ⅱ算法的解集更为集中。

表2中所展示的结果为NICA-II与NSGA算法在相同前提条件下进行多次模块划分优化问题求解平均消耗时间，表3中为两种算法得到的非支配个体数量，用来评估最终解集的准确性。

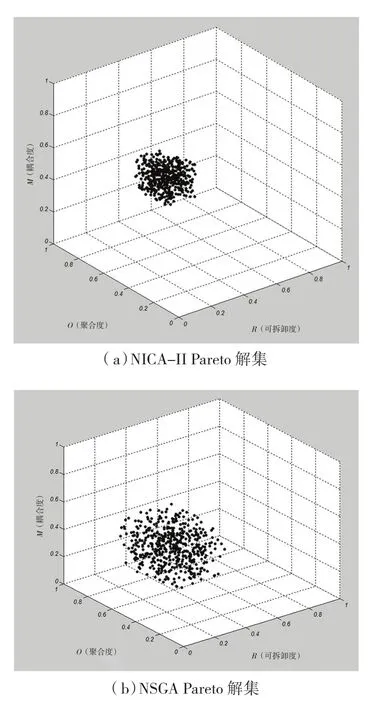
图4 求解的Pareto解集Fig.4 Pareto solution set

表2 NICA-II与NSGA算法平均运算时间的比较

表3 NICA-II与NSGA算法非支配个体数量的比较

通过以上的对比分析结果可以看出，在求解的速度以及解集准确性方面，NICA-Ⅱ算法都优于NSGA算法，因此可以得出结论，改进后的免疫克隆多目标优化算法在模块划分时具有一定的优势。

通过模块单元多目标规划的Pareto选优。根据起落架产品结构的特点，通过计算得到起落架模块单元多目标规划的综合最优解。最终规划方案由5个模块组成：机身模块 {1，2，3，4，9}、转弯模块 {5，8，16，18}、底座模块{10，11，12，14 }、减震模块{6，7，13，17}、连接模块{15，19，20}。

4 结论

（1）模块划分问题是多目标优化问题，可拆卸度是一个难以量化的产品绿色性能指标。本文采用模糊数学理论将产品可拆卸度进行量化计算，并将可拆卸度作为产品模块划分的目标，建立了基于可拆卸度的模块划分多目标优化模型。

（2）本文针对模块划分问题，提出了一种采用改进的NICA-II算法，为了验证该算法的有效性，同时利用NSGA算法进行模块划分问题的求解，通过求解结果的对比，发现在求解时间以及解集准确性方面，改进的NICA-II算法都有较大的优势。

参 考 文 献

[1]DOBRESCU G, REICH Y. Progressive sharing of modules among product variants [J]. Computer-Aided Design, 2003, 35(9)：791-806.

[2]李名. 面向拆卸的产品模块化设计方法研究[D]. 武汉：武汉科技大学, 2015.

LI Ming. Disassembly oriented product modular design method research[D]. Wuhan ：Wuhan University of Science and Technology, 2015.

[3]唐涛, 刘志峰, 刘光复,等. 绿色模块化设计方法研究[J].机械工程学报, 2003, 39(11)：149-154.

TANG Tao, LIU Zhifeng, LIU Guangfu, et al. Green modular design method[J]. Journal of Mechanical Engineering, 2003, 39(11)：149-154.

[4]GU P, HASHEMIAN M, SOSALE S, et al. An integrated modular design methodology for life-cycle engineering[J]. CIRP Annals-Manufacturing Technology, 1997, 46(1)：71-74.

[5]江吉彬, 刘志峰, 刘光复. 基于层次网络图模型的可拆卸性设计[J]. 中国机械工程 , 2003, 14(21)：1864-1867.JIANG Jibin, LIU Zhifeng, LIU Guangfu. Based on the disassembling design of hierarchical network graph model[J]. The Chinese Mechanical Engineering, 2003, 14(21)：1864-1867.

[6]郭伟祥, 刘志峰, 刘光复,等. 基于模块化思想的拆卸序列规划[J]. 计算机辅助设计与图形学学报, 2005, 17(3)：498-504.GUO Weixiang, LIU Zhifeng, LIU Guangfu. Based on the modular thought of disassembly sequence planning[J]. Journal of Computer Aided Design and Graphics, 2005, 17(3)：498-504.

[7]魏巍. 基于环境资源因子的产品平台模块划分方法[J]. 计算机辅助设计与图形学学报, 2016,28(2)：335-344.WEI Wei. Product platform module partition method based on the environmental resources factor[J]. Journal of Computer Aided Design and Graphics, 2016, 28(2)：335-344.

[8]张雷, 彭宏伟, 刘志峰,等. 绿色产品概念设计中的知识重用 [J]. 机械工程学报, 2013, 49(7)：72-79.ZHANG Lei, PENG Hongwei, LIU Zhifeng, et al. The knowledge reuse in the concept of green product design[J]. Journal of Mechanical Engineering, 2013, 49(7)：72-79.

[9]李梁. 机电产品可拆卸性设计理论研究及实现[D]. 淮南：安徽理工大学, 2005.LI Liang. The disassembling design theory of mechanical and electronic products research and implementation [D]. Huainan： Anhui University of Science and Technology, 2005.

[10]魏巍. 基于改进的非支配排序遗传算法的模块化产品多目标配置优化研究[J]. 计算机集成制造系统, 2007, 13(11)： 2092-2098.WEI Wei. Based on the improved multi-objective non dominated sorting genetic algorithm of modular product configuration optimization research[J]. Computer Integrated Manufacturing System, 2007, 13(11)：2092-2098.

[11]尚荣华, 焦李成, 公茂果,等. 免疫克隆算法求解动态多目标优化问题[J]. 软件学报, 2007, 18(11)：2700-2711.SHANG Ronghua, JIAO Licheng, GONG Maoguo, et al. Immune clone algorithm to solve the dynamic multi-objective optimization problems[J].Journal of Software, 2007, 18(11)：2700-2711.

[12]MUHAMAD A S, DERIS S. An artificial immune system for solving production scheduling problems： a review[J]. Artificial Intelligence Review, 2013, 39(2)：97-108.