北斗双频/三频静态精密单点定位性能比较与分析

彭利,王玲,黄文德,满小三

(1.湖南大学 电气与信息工程学院,湖南 长沙 410082; 2.国防科技大学 机电工程与自动化学院,湖南 长沙 410073)



北斗双频/三频静态精密单点定位性能比较与分析

彭利1,2,王玲1,黄文德2,满小三2

(1.湖南大学 电气与信息工程学院,湖南 长沙 410082; 2.国防科技大学 机电工程与自动化学院,湖南 长沙 410073)

针对目前仅北斗全星座提供三频观测数据,而不同线性组合模型影响精密单点定位(PPP)精度和收敛速度的问题,本文着重推导了北斗三频无电离层最优组合精密单点定位数学模型,以此为基础,采用大量实测数据进行北斗双频、三频静态PPP实验。结果表明，相比于北斗双频静态PPP,北斗三频静态PPP在收敛速度和定位精度上有所提高,绝对定位精度可达2～3 cm,与GPS双频精密单点定位水平相当。

北斗卫星导航;精密单点定位;三频精密单点定位;三频线性组合;定位精度

0 引 言

精密单点定位(PPP)技术,即采用单台全球导航卫星系统(GNSS)接收机,利用IGS服务组织提供的精密星历和钟差,基于载波相位观测值进行的高精度定位。由于PPP技术无需地面基准站,作业灵活,而且定位精度不受距离的限制,是继RTK后的又一新技术。经过十几年的发展,GPS PPP技术已经相当成熟,并且广泛应用于高精度测量、低轨卫星定轨、航空测量、地球形变监测等领域。

北斗卫星导航系统(BDS)是我国自主发展、独立运行的卫星导航系统,于2012年底开始正式提供区域服务,预计2020年前建成全球卫星导航系统。截至目前,北斗系统已有20颗卫星在轨运行,分别是5颗GEO、8颗IGSO、7颗MEO,这些卫星均能发射三频信号,频率大小分别为B1: 1 561.098 MHz,B2: 1 207.14 MHz,B3: 1 268.52 MHz[1]。 随着北斗系统的完善和发展,基于北斗三频信号的研究也成为了新的研究热点。文献[1]～[3]研究了北斗三频观测值的线性组合模型及其特性,文献[4]～[9]主要研究了北斗三频观测值在周跳探测、修复等数据预处理方面的应用,文献[10]～[13]则主要针对北斗三频观测值在差分定位及其模糊度解算方面的研究。

然而,目前针对北斗三频信号的研究主要集中在观测值组合理论、差分观测值模糊度解算、数据预处理、误差消除等三频数据处理或者是差分定位方面,只有为数不多的学者对BDS三频PPP进行深入、系统的研究。文献[14]中,郭峰等对北斗三频PPP进行建模,讨论了不同PPP模型之间的关系,并采用实测数据对不同的定位模型进行了动态、静态PPP实验,取得了卓越的研究成果。本文主要分析了BDS三频PPP的定位模型,推导了北斗三频无电离层最优组合精密单点定位数学模型,然后采用BDS精密星历和精密钟差产品,结合大量的实测数据分别进行了GPS、BDS双频、BDS三频静态PPP浮点解试验,并在定位性能方面进行比较与分析。

1 北斗PPP模型与数据处理策略

1.1 传统的观测模型

单一历元时刻,同一台接收机与卫星之间的非差伪距P和载波相位L观测值,其观测方程为

(1)

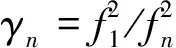
通常,在PPP中,一般采用无电离层线性组合观测值来消除电离层延迟,天顶对流层干分量延迟采用模型进行修正,湿分量延迟进行参数估计,并采用IGS精密星历和精密钟差来消除卫星轨道误差和卫星钟差。其中,IGS发布的精密卫星钟差产品中,包含了卫星端的偏差,而接收机端的偏差则被接收机钟差所吸收。本文假设已经进行了天线相位中心偏移、相位缠绕、潮汐、相对论效应等改正,因此在观测方程中未列出这些项。

传统的消电离层组合PPP,其数学模型为

(2)

1.2 BDS 三频PPP模型

与传统的观测模型不同,北斗系统播发三个频点的信号,三频信号的线性组合观测方程为[21]:

(3)

为了保证几何距离不因组合系数的不同而变化,必须满足条件α+β+γ=1;

假设以m为单位的各伪距和载波相位观测值的噪声标准差分别相等,并分别以σP和σL表示,则组合观测值的伪距和载波相位观测噪声标准差分别为

(4)

为了减小组合观测值的噪声,应寻找合适的组合系数,使得噪声系数最小,即α2+β2+γ2→min.

图1示出了组合系数为1平面与无电离层平面之间的几何关系,从图中可以看出,两平面之间有一条相交线,相交线上有无数个点,即北斗三频无电离层实数组合系数有无穷多组。

对于北斗三频PPP而言,组合系数可能会根据组合噪声、是否保持模糊度整数特性、波长等评判标准的不同而不同。在本文中,选择组合观测值电离层延迟为零时组合噪声最小作为评判标准来选择组合系数,因此可以确定唯一的一组组合系数。表1示出了北斗三频PPP模型的主要特性参数,包括所选取的观测值、组合系数、电离层扩展因子、噪声系数等。为了方便比较,也列出了传统的双频无电离层组合PPP模型的特性参数。(表中,“IF-GPS”代表GPS双频无电离层组合PPP模型,“IF-BDS双频”代表BDS双频无电离层组合PPP模型,“IF-BDS三频”代表BDS三频无电离层组合PPP模型)

表1 双频/三频PPP模型比较

从表1中可以看出,IF-BDS双频PPP模型基本上和IF-GPS模型类似,只是采用了不同频点的信号; 对于相同的北斗三频信号,可以选择其中的两个或三个频点的观测值进行PPP; 此外,还可以看出,IF-BDS双频PPP模型比IF-BDS三频PPP模型更加灵活,尤其是在观测条件不完善、某一频点信号缺失的情况; 但是,IF-BDS三频PPP模型的组合噪声系数比其他方式的无电离层组合PPP模型稍微小一些。

1.3 参数估计及误差处理策略

本文采用表1所示的无电离层组合方式消除电离层延迟一阶项的影响,PPP的待估参数包括接收机的三维坐标、接收机钟差、天顶对流层湿分量延迟以及各颗卫星的组合模糊度浮点解参数,并使用扩展卡尔曼滤波方法进行估计。

表2示出了本文进行BDS三频PPP所采用的数据处理策略。本文所用的卫星轨道和钟差分别采用武汉大学卫星导航定位技术研究中心发布的15 min间隔的精密卫星轨道和GFZ发布的30 s间隔的精密钟差产品; 由于精密卫星钟差产品是基于双频无电离层组合解算得到的,三频无电离层组合PPP在使用该产品时会产生不一致性,需顾及DCBs偏差改正,目前MGEX提供北斗卫星端的DCBs改正产品; 对于对流层延迟,使用Sasstamonion模型改正其干分量,其湿分量则进行参数估计,并对观测值中的相对论效应、潮汐等误差进行改正; 北斗卫星的天线相位中心偏移则采用MGEX提供的BDS卫星的PCO产品; 由于目前尚无权威机构或组织提供BDS接收机端的PCO和PCV信息,所以无法对此项误差进行精确地改正。为了对比分析BDS三频PPP的定位性能,本文也进行了表1所示的BDS双频、GPS双频PPP实验。

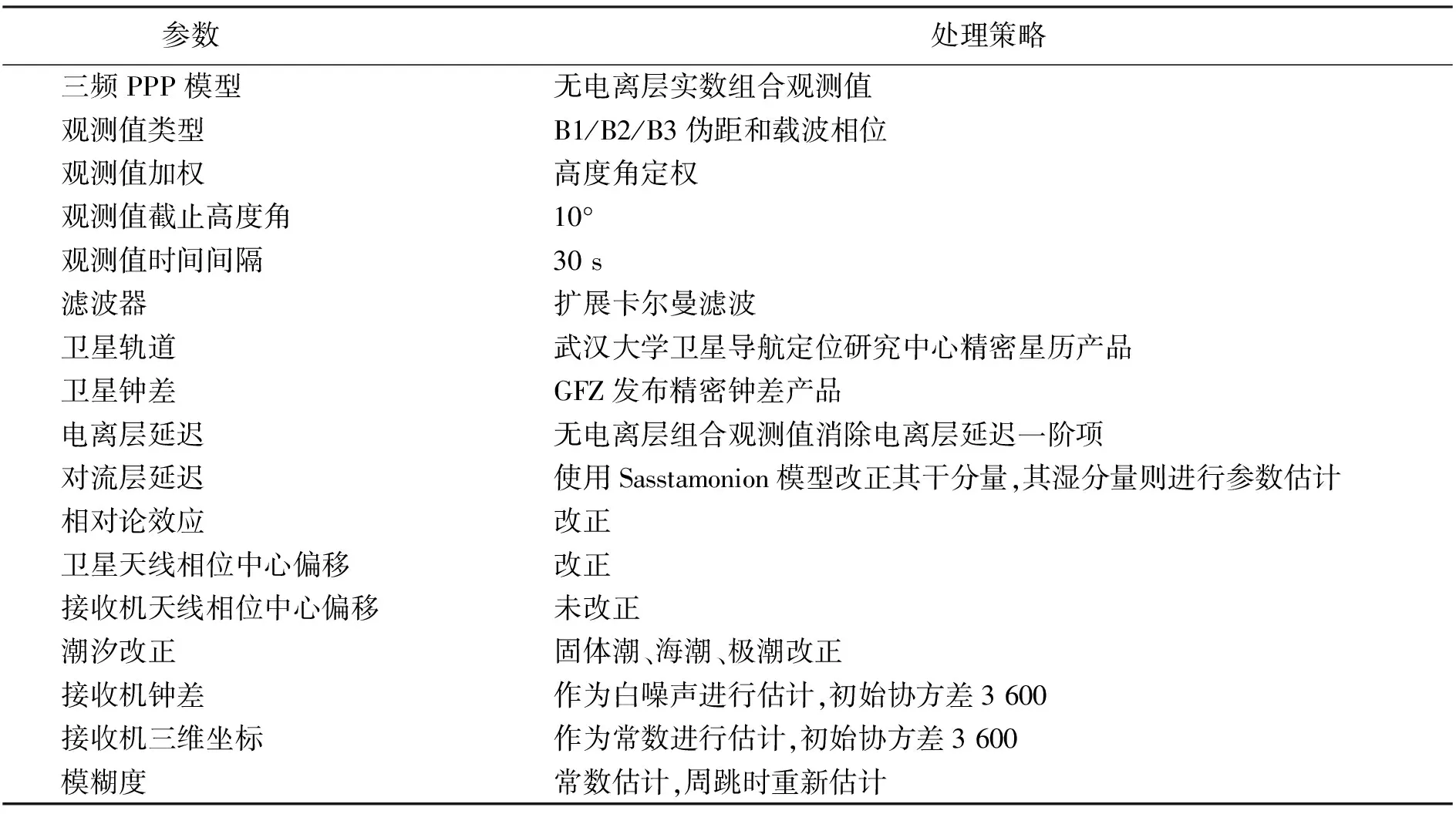
表2 参数估计及其策略

2 BDS双频/三频PPP试验及结果分析

为了分析BDS双频/三频PPP的定位性能,本文采用了2016年1月10日至2016年1月14日共5天澳大利亚Curtin大学5个测站BDS/GPS双系统GNSS观测数据,分别进行了表1所示的BDS B1/B2双频、BDS三频以及GPS PPP实验,本次实验所用的参数估计策略如表2所示。为了分析定位精度,本文将三种方式的定位结果与各测站的坐标真值进行比较,5个测站在ECEF坐标系下的坐标真值如表3所示(坐标真值相关文件下载地址:http://saegnss2.curtin.edu.au/ldc/,文件名为CU-GNSS-receivers-setup.pdf)。

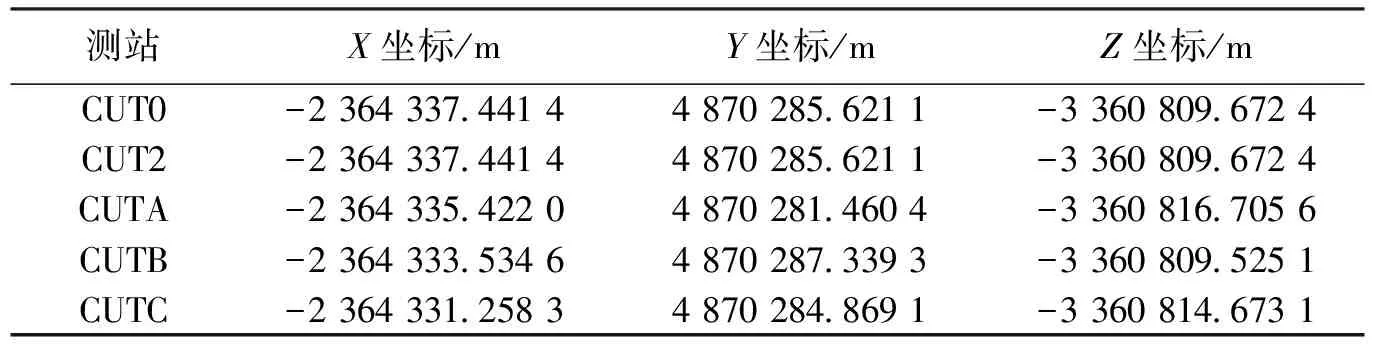
表3 Curtin大学5个测站的坐标信息

图2～图5示出了2016年1月10日和2016年1月12日两天的实验结果,分别为CUT0、CU-TA、CUTB、CUTC四个测站的BDS双频/三频PPP、GPS PPP定位结果与各测站坐标真值的偏差序列(每幅图中的左图为2016年1月10日PPP结果偏差序列,右图为2016年1月12日PPP结果偏差序列)。

图6为五个测站三种定位方式收敛后的三维均方误差图(图中从左至右每一组直方图分别代表CUT0站、CUT2站、CUTA站、CUTB站以及CUTC站三种PPP方式的三维均方误差)。

通过对图2～图6的分析表明:

1) BDS系统两种方式的PPP结果相差较小且很稳定,但是BDS三频PPP的收敛时间和定位精度都要稍优于BDS双频PPP.这是由于本文所使用的BDS三频消电离层观测值组合系数中,B3频点的权重很小,所以三频组合的定位结果和双频组合定位结果差异甚小; 然而,B3频点观测值的加入,进一步提高了组合观测值的精度,所以BDS三频PPP的定位收敛速度和精度有所提高。

2) GPS PPP从收敛时间和定位精度上都要稍优于BDS PPP.出现这种情况的原因可能有以下几个方面:目前GPS的精密星历和精密钟差的精度比BDS的精度要高一些; BDS观测值主要是来自GEO和IGSO卫星,在观测几何构型上可能比GPS稍差。

3 结束语

本文基于武汉大学卫星导航定位技术研究中心发布的15 min间隔的精密卫星星历和GFZ发布的30 s间隔的精密钟差产品,采用澳大利亚Curtin大学5个测站的观测数据,分别进行了GPS PPP、BDS双频PPP以及BDS三频PPP实验。实验结果表明,BDS三频PPP比BDS双频PPP在收敛速度和定位精度上均有所提高,且解算结果比较稳定,三维位置误差为2～3 cm; GPS PPP的收敛速度和定位精度整体上稍优于BDS PPP.随着未来北斗系统的完善以及北斗精密产品精度的提高,BDS PPP的定位精度和收敛速度都将得到进一步提升。由于在本文中只进行了PPP浮点解实验,如何将BDS PPP模糊度固定是接下来的研究重点。

致谢:感谢Curtin University提供BDS/GPS观测数据; 感谢武汉大学卫星导航定位技术研究中心和GFZ提供BDS精密星历和钟差产品; 感谢IGS MGEX提供GPS精密星历、钟差产品以及BDS卫星端PCO产品。

[1] 张小红,何锡扬. 北斗三频相位观测值线性组合模型及特性研究[J]. 中国科学:地球科学, 2015(45): 601-610.

[2] 申俊飞,何海波,郭海荣,等. 三频观测量线性组合在北斗导航中的应用[J]. 全球定位系统,2012,37(6): 37-40.

[3] 刘国超,黄张裕,徐秀杰,等. 北斗三频数据线性组合优化分析[J]. 测绘科学,2015,40(10):69-73.

[4] 刘俊,和秀凤,刘炎雄. 北斗三频非差观测数据的周跳探测与修复方法[J]. 大地测量与地球动力学, 2014,34(8):117-122.

[5] 王华润,柴洪洲,谢恺. 北斗三频无几何、消电离层组合周跳探测方法研究[J]. 大地测量与地球动力学,2015,35(3):406-411.

[6] 姚一飞,高井祥,王坚,等. 北斗三频载波观测值的周跳实时探测与修复[J]. 中国矿业大学学报,2014,43(6):1140-1148.

[7] 刘艳国,秘金钟,李得海. 北斗三频周跳探测方法研究[J]. 测绘科学,2015,40(12):77-80.

[8] 张晨曦,党亚民,王潜心,等. 北斗三频组合在数据预处理中的应用[J]. 测绘通报,2014(10):1-6.

[9] 肖国锐,随立芬,戚国宾,等. 一种改正伪距多路径误差的北斗三频周跳探测与修复方法[J]. 大地测量与地球动力学,2015,35(4):671-675.

[10] 何俊,刘万科,张小红. 北斗短基线三频实测数据单历元模糊度固定[J]. 武汉大学学报(信息科学版),2015,40(3):361-365.

[11] 赵乐文,叶世荣,章太馨,等. 北斗三频RTK定位算法研究[J]. 导航定位与授时,2014,1(3):47-51.

[12] 王兴,刘文祥,陈华明,等. 北斗系统三频载波相位整周模糊度快速解算[J]. 国防科技大学学报,2015,37(3):45-50.

[13] 于嘉琪,王振杰,聂志喜. 短基线北斗三频数据模糊度解算方法的比较[J]. 海洋测绘,2015,35(4):44-47.

[14] GUO F,ZHANG X H,WANG J L,etal. Modeling and assessment of triple-frequency BDS precise point positioning[J]. Journal of Geodesy,2016, 90(11):1223-1235.

[15] 原波. 基于GPS三频非差相位精密单点定位算法研究及程序实现[D]. 北京:清华大学, 2012.

Positioning Performance Comparison and Analysis on BDS Dual-and Triple Frequency Static Precise Point Positioning

PENG Li1,2,WANG Ling1,HUANG Wende2,MAN Xiaosan2

(1.CollegeofElectricalandInformationEngineering,HunanUniversity,Changsha410082,China; 2.CollegeofMechanicalEngineeringandAutomation,NationalUniversityofDefenseTechnology,Changsha410073,China)

At present, only the BDS provides triple frequency observation data, and different linear combination models of observation data influence positioning accuracy and convergence speed of Precise Point Positioning (PPP). This paper deduced the optimal mathematical model of BDS three frequency ionosphere free combination PPP, and carried out experiment of BDS dual-and triple frequency static PPP, using a large amount of measured data. The results show that, triple frequency static PPP obviously improves the positioning accuracy and convergence speed, compared to the BDS dual-frequency static PPP. BDS triple frequency static PPP can reach absolute positioning accuracy of 2～3 cm, with dual-frequency GPS PPP levels.

BDS; precise point positioning (PPP); triple frequency PPP; triple frequency linear combination; positioning accuracy

10.13442/j.gnss.1008-9268.2017.01.011

2016-11-30

P228.4

A

1008-9268(2017)01-0053-06

彭利 (1992-),女,硕士生,主要研究方向为精密单点定位相关技术。

王玲 (1962-),女,教授,博士导师,主要研究方向为现代通信与网络技术等。

黄文德 (1981-),男,博士,讲师,主要从事航天器轨道动力学及卫星导航系统技术研究。

满小三 (1989-),男,硕士,主要从事精密单点定位及RTK相关技术研究。

联系人： 彭利 E-mail: 164500782@qq.com