不同解算条件下PANDA软件静态精密单点定位分析

薛映俊,郭金运,毛继军,刘智敏

(1.山东科技大学 测绘科学与工程学院,山东 青岛266590; 2.山东省国土测绘院,山东 济南 250102)



不同解算条件下PANDA软件静态精密单点定位分析

薛映俊1,郭金运1,毛继军2,刘智敏1

(1.山东科技大学 测绘科学与工程学院,山东 青岛266590; 2.山东省国土测绘院,山东 济南 250102)

分析了PANDA软件精密单点定位的数据处理策略,并采用SDCORS网 81个测站2012年第一周的GPS观测数据进行静态精密单点定位处理,通过得到的各测站年积日001～007的单天解进行统计分析,验证了该软件在山东区域进行精密单点定位的精度及可靠性。通过对比分析,研究了不同卫星截止高度角、不同对流层映射函数、不同星历钟差产品以及不同观测数据时长对其精密单点定位精度的影响。结果显示，当卫星截止高度角设置为10°、采用GMF对流层映射函数、利用精密星历和钟差、观测数据时长超过18 h时,PANDA软件静态精密单点定位的精度能够达到2 cm.

PANDA软件;SDCORS网;精密单点定位;卫星截止高度角;映射函数;星历钟差产品

0 引 言

精密单点定位(PPP)理论与方法是GNSS 领域研究的热点[1-2]。通过PPP技术,利用高精度的星历和钟差产品对单个测站的观测数据进行处理,能够获得高精度定位结果,PPP具有成本低、工作量小的特点[3]。目前PPP技术的实现主要是基于GPS单系统[4],定位的精度已经实现了静态mm-cm级、动态cm-dm级[5-10]。随着一些新的算法和误差改正模型的不断改进和提出,IGS提供的星历和钟产品的精度不断提高以及硬件性能的不断完善[11-12],精密单点定位理论也进一步完善,PPP定位的精度不断提高[13],在精密测量、变形监测以及航空测量等多个领域都得到了广泛应用[14-15]。

当前国际上有多个PPP处理软件,例如美国喷气动力实验室(JPL)研制的非差定轨定位软件GIPSY[16]和瑞士伯尔尼大学研制的软件BERNESR[17]以及武汉大学卫星导航定位技术研究中心研发的PANDA[18]。其中GIPSY只提供可执行文件,采用非差方式处理GPS观测值,但在模糊度解算时采用差分模式[19]。BERNESE软件的精密单点定位是采用非差方法进行,但整网平差却是利用双差进行。而PANDA软件采用的是非差模式,通过逐个历元建立观测方程[15,20],来实现测站的静态、动态定位,与国际GNSS服务组织(IGS)精密星历比较,测站静态定位精度在17 mm左右。并且该软件近年来不断引入新的计算方法与误差模型,在模糊度固定、参数估计、动力学模型等关键技术研究方面不断突破,软件的功能不断成熟与完善。PPP模块中采用了地面跟踪网数据估计单差的初始相位延迟(Uncalibrated Phase Delays),来去掉单差模糊度的小数部分,从而固定单差模糊度的新方法。利用此方法可以固定80%的独立模糊度,固定解相比浮点解精度也提高了30%左右[18]。因此PANDA软件得到了越来越广泛应用。

为了对山东省CORS(SDCORS)网数据进行快速高精度处理,本文结合SDCORS网的观测数据,利用PANDA 软件的PPP模块进行静态精密单点定位处理。通过结果分析该软件精密单点定位的稳定性及可靠性,并且进一步分析卫星截止高度角、对流层投影函数、最终星历及钟差和快速星历及钟差以及不同时长的观测数据对其定位精度的影响。

1 PANDA软件精密单点定位

PANDA软件的精密单点定位模块主要采用非差处理模式,为了探测和修复周跳,对数据编辑和周跳探测采取单站数据处理方法[21]。并通过引入新的模糊度参数来处理未修复的周跳,在残差编辑模块的质量控制部分对未完全探测出的小周跳与粗差进行处理[18]。当前该软件已经能够处理包括GPS、卫星激光测距(SLR)、K频段测距(KBR)、卫星姿态与加速度计等多种类型观测数据。

PANDA软件的精密单点定位处理首先要读取GPS标准数据格式的RINEX文件,包括观测文件(O文件)、广播星历文件(brdc文件)、精密星历和钟差文件(sp3和clk文件)等。GPS的数据质量是实现高精度定位的基础,因此观测数据的预处理也就尤为重要[22]。预处理的好坏对定位精度的高低有着直接影响,而在这其中如何准确、可靠地探测出相位观测量中的周跳最为关键[15]。由于卫星信号失锁、接收机硬件以及各种环境因素的影响,在实际观测量中周跳和观测噪声是同时存在的,当观测噪声较大时,会将小的周跳掩盖,结果就会出现一定偏差,因此有效的探测与修复周跳来获得质量良好的观测值是进行参数求解的重要前提[23]。PANDA软件采用的清除周跳的方法是基于Blewitt提出的TuiboEdit方法[21]的改进,利用双频双P码组合观测值修复周跳。在软件非差定位中,不考虑测站之间的相关性,待估参数主要有接收机三维坐标、接收机钟差、对流层延迟参数、电离层参数以及模糊度等[24]。参数估计是精密单点定位的关键,参数估计的方法直接影响到定位处理的精度和效率。PANDA软件的参数估计模块包括均方根信息滤波[25]和最小二乘两个估计器,利用新的模糊度参数来估计被探测到但未被修复的周跳。均方根信息滤波包括前向均方根信息滤波器(SRIF)和后向均方根信息平滑器(SRIS),SRIF具有较高的数值稳健性和计算高效性,能有效克服滤波器的发散,SRIS能够估计随机过程(如钟差,对流层延迟,大气阻力系数等)参数,适合于观测数据实时处理[26]。而最小二乘估计器主要应用于事后处理,这有利于节省计算时间和基于观测值残差的数据再编辑。图1示出了PANDA软件精密单点定位的处理流程。

2 实验结果及分析

2.1 观测数据

实验采用了SDCORS网的观测数据,该系统整合了山东省已建CORS站点,构成了全省统一的高精度、高时空分辨率、高覆盖率、实时快速的卫星定位连续运行综合应用服务网,是“数字山东”的空间信息基础设施之一[27]。SDCORS系统自运行以来,截止目前在网运行的参考站数达到157个,可以兼容拓普康、天宝、徕卡等GPS厂商的软硬件。CORS网中各测站的观测采样间隔为30 s。为了验证PANDA软件精密单点定位的精度以及在不同影响因素条件下对定位精度的影响,选取SDCORS网2012年年积日001到007第一周的观测质量良好的81个站的观测数据,进行静态精密单点定位处理。

2.2 精密单点定位

利用PANDA软件的精密单点定位模块,将这81个站的观测数据O文件以及从IGS上下载的星历、钟差等文件导入软件进行静态精密单点定位处理。通过软件对5°、10°、15°、20°、25°、30°、35°、40°等不同卫星截止高度角阈值的设置;对NMF/GMF/CFA等不同对流层映射函数的选取;对精密星历和钟差与快速星历和钟差的采用;对不同时长的连续观测数据的采用,分批次进行处理得到精密单点定位的结果。这里,将SDCORS数据自动化处理及分析系统所提供的2012年各测站坐标的年解作为参考值。由于该系统综合了GAMIT/GLOBK和BERNESE两大高精度的GPS数据处理软件,并利用2012年整年的观测数据进行处理,所得到的各测站坐标的精度和可靠性都能满足参考需要,所以采用该系统提供的坐标值作为参考值。通过将实验精密单点定位处理得到的定位结果和参考坐标进行比较,来分析PANDA软件精密单点定位的精度以及不同影响因素对定位精度的影响。

如图2所示,将卫星截至高度角阈值设置为10°、对流层映射函数采用GMF、利用精密星历和钟差进行PPP处理时,所获得81个测站连续7日单天解的平均值与参考坐标比较的统计结果。其中dx、dy、dz分别表示为各测站在X、Y、Z三个方向上的坐标差值,M为综合三个方向的点位误差。

从图2可知,在X、Y、Z三个方向上所有测站平均的坐标差值分别为0.26 cm、-0.71 cm、-0.54 cm,综合三方向点位误差M为1.24 cm.各方向较差和综合三个方向点位误差均在2 cm以内,这从一方面证明了PANDA软件的PPP精度与国际先进软件水平相当。所有测站各方向最大坐标差值为1.70 cm,最小坐标差值为-2.25 cm,均在±3 cm以内。并且从图2可以看出在总体趋势上,各方向坐标差值有所波动,但波动幅度较小,精度相差不大。这主要是由软件采用误差模型改正精度的影响产生的。从一方面也说明了PANDA软件的PPP结果比较稳定,可靠性较好。

如表1所示为分别采用5°～40°每间隔5°的不同卫星截止高度角阈值设置,利用精密星历和钟差以及GMF对流层映射函数,对81个测站连续一周的观测数据进行PPP处理。将解算得到的所有测站连续7日单天解的平均值与参考坐标作差,再对所有测站的综合三个方向点位误差进行统计的。统计结果显示,当卫星截止高度角设置为10°时,所有测站点位误差均值和中误差RMS值分别为1.19 cm和1.35 cm,均在2 cm以内。当高度角设置逐渐减小或增大时,点位误差均值和中误差RMS值也逐渐增大,且当卫星高度角增大时尤为明显。可以看出当高度角为10°左右时,软件的定位精度最高;当高度角超过25°时,最大点位误差超过5 cm,点位误差均值和中误差RMS值也都超过2 cm,定位精度明显变差,已经不能满足精密单点定位的精度要求。这是由于当卫星截止高度角降低时,观测到的卫星数目虽然有所增多,但是多路径效应和周跳会明显增加;卫星高度角升高时,虽然多路径效应和周跳的影响变小,但可见卫星数目也在减少,使得观测数据结构变差。两种情况都会使得定位精度降低。

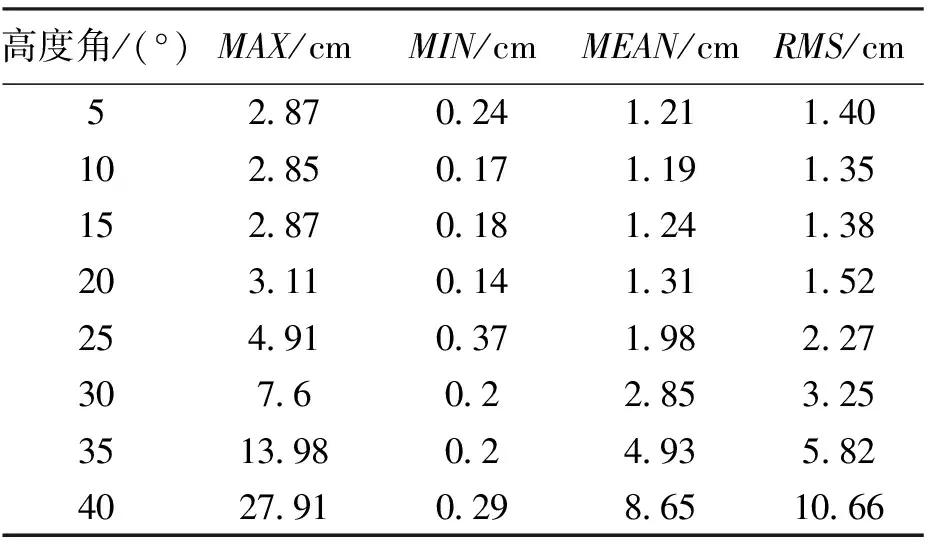
表1 不同高度角设置时精密单点定位结果精度对比

卫星截止高度角设置为10°,采用精密星历和钟差,分别利用CFA、NMF、GMF三种对流层映射函数,对81个测站一周观测数据进行PPP处理。将解算得到的各测站7日单天解分别与参考坐标作差,并计算出综合各方向点位误差,再对每天所有测站平均的点位误差进行统计。如图3所示，从图3可知,三种映射函数对精密单点定位结果精度的影响差别并不大,平均点位误差相差均在3 mm以内。其中GMF模型的定位精度相对最好,CFA次之,NMF再次之。CFA模型是由Marin连续性映射函数改进得来的,其系数式是从双层射线跟踪分析得出的。NMF 模型是根据北半球一年中的电波资料所建立的,由于缺乏其他的客观数据,所以该经验模型的模拟过程显得过于简单。而GMF 模型是采用数值天气模型(NWM)提供的高精度全球对流层折射率来解算延迟量,其参数是建立WCMWF(欧洲中期天气预报中心)提供的气压、温度和湿度等分析数据基础上,基于三维大气场数据内插得到的,并且考虑到测站经度对解算的影响的气象模型,所以精度要优于另外两种模型。并且,三种对流层映射函数的定位平均点位误差均在3 cm以内,总体上变化趋势相似,这不仅反映了该软件具有较高的精密单点定位精度,而且定位结果也具有较好的稳定性,这与PANDA软件逐历元建立观测方程有关。

卫星截止高度角设置为10°,采用GMF映射函数,分别利用IGS提供的精密星历、钟差产品和快速星历、钟差产品,对测站进行PPP处理,将解算结果进一步计算得到所有测站7日单天解的综合三方向点位误差,再将每天所有测站平均的点位误差进行统计，图4示出了统计结果。从图4可以看出,使用两种产品的解算结果相差不大,存在几个毫米的偏差,精度在同一量级。但利用精密星历、钟差的解算精度比快速星历、钟差的解算精度要高,整体都在2 cm以内。这是由于IGS给出的两种产品的精度和采样率指标虽然相同,但时延和更新率不同,而且最终产品是综合了全球7个IGS分析中心的解算结果,因此最终产品的精度和可靠性要高于快速产品。

当卫星截止高度角设置为10°,采用精密星历和钟差,利用GMF映射函数时,分别采用81个测站年积日002的,从0 h开始每增加2 h的不同时长观测数据进行PPP处理。将得到的每个观测时长的所有测站平均的点位误差进行统计，图5示出了统计结果。从图5可以看出,Z方向的定位精度相对较好,要优于其他两个方向。观测数据的时长越长,定位的精度也就越高。当观测时长少于10 h时,软件的PPP定位精度较差,平均中误差大于3 cm;当观测数据时长超过18 h时,定位精度才能得到保证,点位平均中误差小于2 cm.因此,利用PANDA软件进行静态精密单点定位处理时,要保证观测数据时长大于18 h.

3 结束语

利用PANDA软件进行静态精密单点定位时,解算结果的精度较高,稳定性和可靠性也较好。并且从实验结果可以看出PANDA软件的精密单点定位结果存在着一定的系统性偏差,这主要是由于对流层延迟以及其他误差的影响。因此,仍需要对这些误差改正模型进行进一步研究。此外,卫星截止高度角的选取对软件精密单点定位的精度有着较大影响,这是由于当卫星截止高度角过低时,受多路径影响严重,观测数据噪声较大;当卫星截止高度角过高时,会过滤掉部分卫星,使得有效观测数据减少[28]。在实际数据处理过程中,当卫星高度角在10°左右时,定位精度最高,当卫星高度角减小或增大时,相应的定位精度也会降低。而利用不同对流层映射函数进行PPP处理则有着不同的定位精度。在CFA、NIEL、GMF三种映射函数中,采用GMF模型的定位精度相对较好。使用最终产品和快速产品的精密单点定位解算结果有所差别,但精度在同一量级,其中最终产品的精度和可靠性要高于快速产品。利用PANDA软件进行PPP处理时,观测数据时长对定位的精度有一定影响,一般当观测数据时长超过18 h,才能保证软件单天解的精度。所以,在利用PANDA软件进行静态精密单点定位时,选择合适的卫星高度角、合适的对流层映射函数、利用精密星历和钟差以及采用适宜时长的观测数据时,会得到较高的定位精度。

[1] KOUBA J,HEROUX P.Precise point positioning using IGS orbit and clock products[J].GPS Solutions,2001,5(2):12-28.

[2] 姜卫平,邹璇,唐卫明.基于CORS网络的单频GPS实时精密单点定位新方法[J].地球物理学报,2012,55(5): 1549-1556.

[3] 鲁洋为,王振杰. Bernese 5.0软件下的精密单点定位精度分析[J].测绘通报,2016,(2): 22-25.

[4] 周超. 基于GPS/BDS融合的精密单点定位及精度分析[J].全球定位系统,2016,41(2):92-95.

[5] 孟祥广,郭际明.GPS/GLONASS 及其组合精密单点定位研究[J].武汉大学学报(信息科学版),2010,35(12): 1409-1413.

[6] 蔡昌盛,朱建军,戴吾蛟,等.GPS/GLONASS组合精密单点定位模型及结果分析[J].武汉大学学报:(信息科学版),2011,36(12): 1474-1417.

[7] 张小红,郭斐,李星星,等.GPS/GLONASS 组合精密单点定位研究[J].武汉大学学报(信息科学版),2010,35(1): 9-12.

[8] 蔡昌盛,戴吾蛟,匡翠林,等.利用UofC消电离层组合的GPS/GLONASS精密单点定位研究[J].武汉大学学报(信息科学版),2012,37(7): 827-830.

[9] 刘站科,付文举,黄观文,等. GPS/GLONASS组合精密单点定位[J]. 测绘通报,2016(7):6-10.

[10] 李征航,黄劲松.GPS测量与数据处理[M].2版.武汉:武汉大学出版社,2010.

[11]HATCH R.Satellite navigation accuracy:Past,present and future[C]//The 8th GNSS Workshop,Korea, 2001.

[12]GAO YANG, CHEN KONGZHE. Performance analysis of precise point positioning using Real-time orbit and olockproducts[C]//The 2004 international symposium on GNSS/GPS,Sydney, 2004.

[13]张小红,李星星.非差模糊度整数固定解PPP新算法及实验[J].武汉大学学报(信息科学版),2010,35(6):657-660.

[14]安向东.GPS与北斗伪距单点定位性能对比分析[J].全球定位系统,2014,39(3):8-14.

[15]耿涛,赵齐乐,刘经南,等. 基于PANDA 软件的实时精密单点定位研究[J]. 武汉大学学报(信息科学版),2007, 32(4):312-315.

[16]WEBB F H, ZUMBERG J F. An introduction to GIPSY/OASIS2II precision software for analysis of data from Global Positioning System [R]. Jet Propulsion Laboratory, California Institute of Technology, 1993.

[17]DACH R,HOGENTOBLER U,FRIDEZ P,eta1.Bernese GPS software version 5.0[M].Berne: University of Bern,2007.

[18]施闯,赵齐乐,楼益栋,等.卫星导航系统综合分析处理软件PANDA及研究进展[J].航天器工程,2009,18(4):64-70.

[19]肖根如,甘卫军,殷海涛.GIPSY 软件的GPS 数据处理策略及应用[J].地球物理学进展,2010,25 (4):1508-1515.

[20]方荣新,施闯.高采样率GPS数据非差精密处理方法及其在地震学中的应用研究[D].武汉:武汉大学,2010.

[21]BLEWITT G.An automatic editing algorithm for GPS data[J].Geophysical Research Letters, 1990, 17(3):199-202.

[22]李国伟,郭金运,王书阳,等. 基于动态单点定位的GPS数据质量指标研究[J]. 山东科技大学学报(自然科学版),2013,32(3):89-94.

[23]郭金运,宗干,李旺,等.GPS单星单历元模糊度与电离层延迟分类解算[J].山东科技大学学报(自然科学版),2015,34(1):54-60.

[24]谭争光,郭金运,宗干,等. PANDA和BERNESE软件的PPP比较分析[J]. 全球定位系统,2013, 38(5):60-64.

[25]GERALD J B. Factorization methods for discrete sequential estimation [M]. New York: Academic Press, 2006.

[26]赵齐乐,刘经南,葛茂荣,等. 用PANDA对GPS和CHAMP 卫星精密定轨[J].大地测量与地球动力学,2005,25(2):113-116.

[27]张海平,高士民,周长志,等.SDCORS系统测试与技术性能分析[J]. 全球定位系统,2013, 38(3):62-64.

[28]王楠,张郁. 卫星高度角对GPS测量精度的影响研究[J]. 武汉理工大学学报(信息与管理工程版),2012,34(5):562-564.

PANDA Static PPP Solutions with Different Strategies

XUE Yingjun1,GUO Jinyun1,MAO Jijun2,LIU Zhimin1

(1.CollegeofGeomatics,ShandongUniversityofScienceandTechnology,Qingdao266590,China; 2.ShandongProvincialInstituteofLandSurveyingandMapping,Jinan250102,China)

The data processing strategy of PANDA software precise point positioning are analyed,and using the GPS data of 81 stations in SDCORS network for the first week of 2012 to carry out the static precise point positioning. The single day solution of one week for each station are analysised,the accuracy and reliability of the software precise point positioning in Shandong area are verified.The effect of the precise point positioning accuracy on different satellite cut-off angle,different mapping function,different ephemeris products,different length of observation data are studied. The conclusion indicates that when the satellite cut-off angle is set to 10 degrees, using GMF mapping function, using the precise ephemeris and clock correction, observation data for more than 18 hours, PANDA software static precise point positioning accuracy can reach 2 cm.

PANDA; SDCORS network; Precise Point Positioning; satellite cut-off angle; mapping function; ephemeris and clock products

10.13442/j.gnss.1008-9268.2017.01.006

2016-09-21

国家自然科学基金(批准号：41374009); 国家科技基础性工作专项(编号：2015FY310200); 山东省自然科学基金(批准号：ZR2013DM009)

P228.4

A

1008-9268(2017)01-0028-06

薛映俊 (1993-),男,硕士生,主要从事空间大地测量等研究。

郭金运 (1969-),男,博士、教授、博导,主要从事空间大地测量、海洋大地测量和物理大地测量。

联系人： 薛映俊 E-mail:1720243832@qq.com