不同随机模型在GPS单历元定位中解算性能分析研究

陈西斌

(1.长春市测绘院,吉林 长春 130021;2.中国矿业大学 环境与测绘学院,江苏 徐州221116)



不同随机模型在GPS单历元定位中解算性能分析研究

陈西斌1,2

(1.长春市测绘院,吉林 长春 130021;2.中国矿业大学 环境与测绘学院,江苏 徐州221116)

基于GPS单历元解算中随机模型对解算精度的重要性,分析了常见的四种随机模型建模条件。通过实测基线算例从流动站定位结果与定位标准偏差对它们进行分析与比较,明确了不同随机模型的适用条件,为进一步提高GPS单历元定位精度提供了理论基础。

随机模型;单历元;内符合精度;track模块;GAMIT

0 引 言

GPS单历元定位中,由于观测条件数少,组成方程个数较少,为得到精度较高的整周模糊度与协方差矩阵,选择合适的随机模型十分重要。在双差方程解算中,选择不同的随机模型则赋予双差观测值的权不同,这不仅对基线解算有影响,而且关系到模糊度的搜索范围。本文通过两组具有代表性的短基线数据,将四种随机模型进行定位精度分析与比较,得出一些有益的结论。

1 单历元观测方程随机模型

不管是非差模型、双差模型,还是组合模型,在组成改正数方程时,都需要观测值的先验信息,即观测值的随机模型。常见的双差形式为测站间与卫星间作差,可表示为[1]

(1)

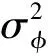
(2)

不同的随机模型对解算函数模型影响很大,下文将分别介绍常见的随机模型适用条件。

1.1 等权随机模型

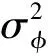
(3)

1.2 高度角随机模型[3]

该随机模型是将卫星处于某一时刻的高度角计算并建立的模型,其认为载波观测值的精度与高度角相关。一般情况下高度角不同,信号传播的路径也不相同,随着高度角增加,信号传播路径减少,大气延迟误差与多路径误差影响减弱。观测值方差可以表示为高度角数值的函数:

(4)

f函数常见的有指数函数,正切函数,正弦函数,余弦函数。

1) 指数函数模型[3]

(5)

式中:σ0为卫星高度角为90°时载波观测精度的均方差;a为比例系数;ε(t)为卫星高度角与时间成函数的数值;ε0为两测站间共视卫星的高度角最大值。文献[4]给出参考值，如表1所示。

表1 指数模型的参考值

2) 正弦函数模型

(6)

式中,E为卫星高度角。上述高度角随机模型并不能很好地反映低高度角观测精度,实际运用中常采用改进后的正弦函数模型[5]:

(7)

式中,a、b常取经验值a=4 mm,b=3 mm.

3) 正切函数模型[6]

(8)

1.3 载噪比随机模型

(9)

式中,Ci可用式(10)计算而得:

(10)

(11)

式中: Δ为理论值与实际观测值差值;a为经验系数一般取2.

1.4 信号强度随机模型

(12)

(13)

2 实验分析

1) 实验一

实验数据来自中国矿业大学(徐州)南湖校区数据采集试验场地,基线长约为91.3 m,基站与流动站高差较小,数据采样间隔为1 s,采用天宝R8接收机,观测时段为2014年10月2日,采用500个连续历元,卫星截止高度角为10°,在后期数据转换中增加CN0观测值输出。利用GAMIT软件包中track模块进行解算,对track模块增加这四种随机模型,得到流动站北(N)、东(E)、高程(U)三方向的定位结果,并利用内符合精度(STD)进行精度分析,如图1所示和表2所示。

从图1可以看出,等权模型在N、E、U三个方向定位结果最差,高度角模型、信号强度模型、载噪比模型定位结果相对较为平滑。

从表2可以看出,除等权模型以外的三种随机模型中定位精度由高到低为载噪比模型、信号强度模型、高度角模型。这主要由于一般低高度角卫星的观测值中噪声较多,其中包括多路径效应的影响,所以高度角随机模型可以部分地减少多路径的影响。与高度角模型相比,信号强度与载噪比更能够反映载波观测值的质量,尤其是卫星出现遮挡或者测站环境较复杂时,卫星的高度角也许数值较大,但其信号强度与载噪比数值比一般情况下较小。信号强度模型与载噪比模型解算结果大致相同,当数据转换无载噪比数值输出时,可以用载波强度代替载波噪声比来求取观测值的先验信息。

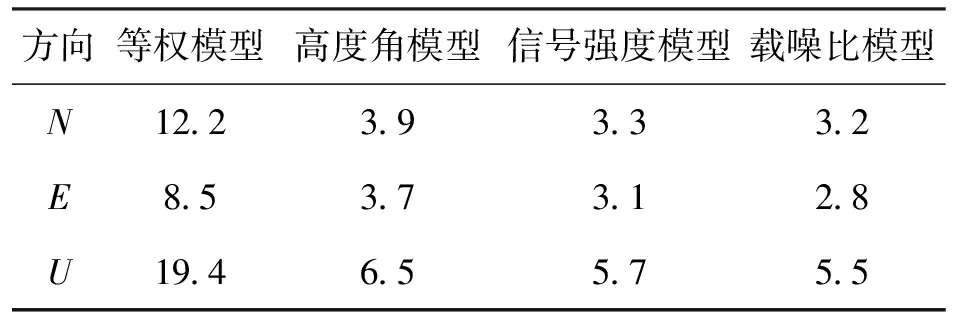
表2 四种不同模型计算的流动站 坐标STD值 单位：mm

2) 实验二

实验数据来自环测楼顶实验场地,基准站架设在环测学院楼顶基准台上,流动站架设在南湖校园内道路旁,基准站与流动站高差大约为24.87 m,基线长约为1.09 km,数据采样率为1 s,卫星截止高度角设置为10°,解算软件同实验一,定位结果如图2所示和表3所示。

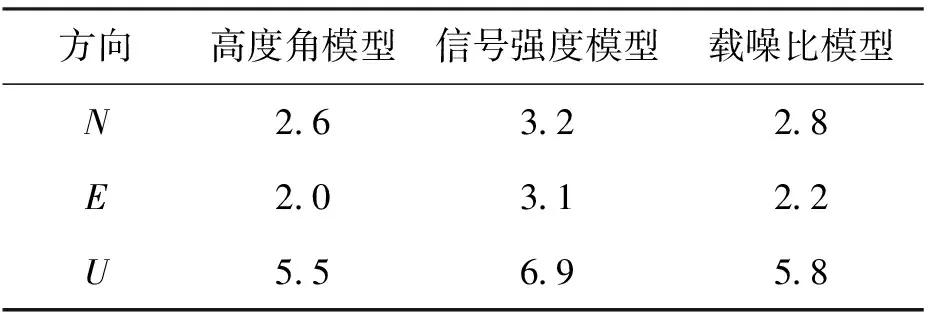
表3 三种不同模型计算的流动站 坐标STD值 单位：mm

从表3中可以看出,高度角随机模型定位精度最高,信号强度与载噪比模型定位精度较差。这主要由于基准站与流动站存在着将近25 m的高差,从而双差方程中残余的对流层误差数值较大。而由于高度角为对流层延迟的函数形式,因此观测方程中使用高度角随机模型有利于消除残余大气延迟误差的影响。

3 结束语

通过利用等权模型、高度角模型、信号强度模型、载噪比模型对不同长度的、高度差较大的两组基线进行数据处理,比较分析每种随机模型的定位结果。可以得到以下结论:

1) 等权模型是一种理想化模型,尽量不采用该模型。高度角模型、信号强度模型、载噪比模型定位结果均优于等权模型。

2) 高度角随机模型在基准站与流动站之间高差较大的情况下益适用,可更加有效地削弱残余对流层延迟误差;基线解算结果表明载噪比随机模型与信号强度随机模型的定位效果基本一致,当原始数据中有信号载噪比输出时可替代信号强度建立载噪比随机模型。

[1] 孟黎,徐杰.GPS观测量的随机模型研究[J]. 工程勘察, 2011(1): 73-77.

[2] 王振杰,方稚. GPS数据处理中实时随机模型的估计方法[J]. 海洋测绘, 2014(6): 29-31，35.

[3] 徐鹏.基于卫星高度角的GPS观测量随机模型分析[J]. 测绘技术装备, 2013(1): 40-42.

[4] 刘志强,黄张裕. GPS随机模型最优不变二次无偏估计算法及实现[J]. 测绘科学, 2008，33(16): 158-159,80.

[5] 刘超,王坚,路鑫，等.GPS载波相位观测值随机模型的比较研究[J]. 测绘科学, 2010，35(6): 151-154.

[6] 郭秋英,蔡菲.GPS载波相位双差观测量随机模型估计的新方法[J]. 山东建筑大学学报, 2009(5): 411-416.

[7] 李博峰,沈云中,徐培亮. 不同GPS接收机观测值的随机模型评估[J]. 科学通报, 2008，53(16): 1967-1972.

[8] 邱卫宁,齐公玉,邹进贵，等. 不同随机模型在GPS单历元变形解算中的应用研究[J]. 测绘通报, 2011(10): 5-7.

[9] 张莎莎,郑黄成,李信，等. 基于高度角的GPS单点定位随机模型研究[J]. 城市勘测, 2014(5): 30-31,34.

[10] 戴吾蛟,丁晓利,朱建军.基于观测值质量指标的GPS观测量随机模型分析[J]. 武汉大学学报(信息科学版), 2008，33(7): 718-722.

Research on Different Stochastic Model in GPS Single Epoch Position Resolution

CHEN Xibin1,2

(1.ChangchunSurveyingandMappingInstitute,Changchun130021,China; 2.ChinaUniversityofMiningandTechnology,SchoolofEnvironmentalScienceandSpatialInformatics,Xuzhou221116,China)

Analyzing the common conditions of four kinds of stochastic model based on the importance of GPS single epoch solution. It is defined the applicability conditions of different stochastic models, according to analysising and comparing the results and std of mobile station from baseline example. it provides bases for further improving the positioning accuracy of GPS single epoch.

Stochastic model; single epoch; STD; track module; GAMIT

10.13442/j.gnss.1008-9268.2017.01.007

2016-11-11

江苏高校优势学科建设工程资助项目(编号：PAPDSA1102)

P228.4

A

1008-9268(2017)01-0034-05

陈西斌 (1987-),男,黑龙江虎林人,硕士,助理工程师,主要研究方向为GNSS数据处理与GAMIT、Bernese软件研究等工作。

联系人: 陈西斌E-mail:chenxibin1203@126.com