基于模糊逻辑的自适应强跟踪卡尔曼滤波在GPS定位中的应用

胡辉,颜瑜军,欧敏辉,彭雄明

(1.华东交通大学 信息工程学院,江西 南昌 330013；2.武汉梦芯科技有限公司,湖北 武汉 430073)



基于模糊逻辑的自适应强跟踪卡尔曼滤波在GPS定位中的应用

胡辉1,颜瑜军1,欧敏辉1,彭雄明2

(1.华东交通大学 信息工程学院,江西 南昌 330013；2.武汉梦芯科技有限公司,湖北 武汉 430073)

当载体速度频繁发生突变时,针对卡尔曼滤波在GPS定位解算中对系统模型依赖性强、鲁棒性差的问题,提出了一种基于模糊逻辑的自适应强跟踪卡尔曼滤波算法。该算法主要利用模糊逻辑自适应控制器监测系统输出的残差均值,并根据模糊规则动态调整弱化因子,从而对强跟踪滤波器中次优渐消因子进行自适应调整,来实现抑制载体突变影响。仿真结果表明:该算法在载体突变的跟踪精度高于扩展卡尔曼滤波和强跟踪卡尔曼滤,其稳定性也有所提高。

GPS;模糊逻辑自适应控制器;强跟踪滤波器;卡尔曼滤波器

0 引 言

标准的卡尔曼滤波器(KF) 是在已知系统模型和量测模型以及系统噪声和量测噪声的统计特性下才会获得理想的滤波效果。但是,当系统模型参数与实际过程参数存在较大差异时,KF的估计精度会大大下降,甚至发散,且KF在系统达到平稳状态时,将丧失对突变状态的跟踪能力,扩展卡尔曼滤波器(EKF) 也存在类似的缺点[1]。为此,文献[2]～[5]的研究者对EKF提出了引入渐消因子进行自适应处理的方法,采用渐消因子来抑制滤波器的记忆长度,以便充分利用现时的观测数据,减小陈旧量测值的影响,这类处理方法处理的基准是认为系统状态协方差过小,通过在系统状态协方差上乘以渐消因子来实现稳定跟踪,但当系统模型存在较大误差或状态突变较大的情况下,其渐消因子调节的效果难以区分且渐消因子的计算复杂,因此如何选取合适的渐消因子是该方法面临的一个难题。而文献[6]～[9]的研究者在引入渐消因子方法的基础上提出了基于模糊控制的自适应滤波方法,利用模糊逻辑自适应控制器(FLAC)来在线调整卡尔曼滤波器,对渐消因子进行自适应模糊调节,从而防止滤波器发散,目前这类算法主要在组合导航系统中数据融合比较成功。本文针对卡尔曼滤波在GPS定位解算中对系统模型依赖性强、鲁棒性差的问题,提出了一种基于模糊逻辑的自适应强跟踪卡尔曼滤波(FASTKF) 算法,该算法采用一种FLAC来动态调整该弱化因子,从而对次优渐消因子进行“在线”自适应调整,进一步提高滤波器跟踪精度,仿真结果表明，FASTKF具有应对突变状态的强跟踪能力,且估计精度高等特点。

1 GPS定位解算模型

将EKF应用于GPS定位解算中,首要是建立状态模型和观测模型。定义Xk为系统状态向量,Zk为系统观测向量。

(1)

Zk=[ρi,k,di,k],

(2)

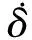
1.1 状态方程建立

在位置速度(PV)模型中,状态量包括三个正交方向上的位置和速度、钟差、钟漂,其中每个方向上的位置和速度所含噪声是相互独立的,相关系数为零。系统的离散状态转移方程:

Xk=ΦXk-1+Wk-1，

(3)

式中：Φ为离散时间域的状态转移系数矩阵；Wk-1为系统噪声，由连续时间域F(t)推导获得[10]:

(4)

(5)

式中:

1.2 观测方程建立

系统的观测方程,伪矩和系统状态参数的关系为

ρi,k=|rr,k-ri,k|+cδtk+εi,k

=[(xr,k-xi,k)2+(yr,k-yi,k)2+

(zr,k-zi,k)2]1/2+cδtk+εik,

(6)

式中:ρi,k为第i颗卫星k时刻的伪矩；rr,k为接收机k时刻的位置；ri,k为第i颗卫星k时刻卫星的位置；εi,k为第i颗卫星k时刻总的测量误差,εi,k用白噪声进行建模。其伪矩方程中有四个未知的变量,接收机的位置(xr,k,yr,k,zr,k)以及接收机时钟偏差δtk； 其k时刻第i颗卫星的位置为(xi,k,yi,k,zi,k),其由导航电文提取后求得。

多普勒频率测量值的计算:

di,k= [(xr,k-xi,k)(vx,k-vxi,k)+(yr,k-

yi,k)(vy,k-vyi,k)+(zr,k-zi,k)

(vz,k-vzi,k)]/[(xr,k-xi,k)2+

(7)

式中:vx,k,vy,k,vz,k分别为接收机在X、Y、Z方向的速度；vxi,k,vyi,k,vzi,k分别为第i颗卫星X、Y、Z方向的速度。

对观测方程式(6)和式(7),可以写成矩阵的形式

Zk=HkXk+Vk,

(8)

式中:Xk为k时刻点的状态向量；Vk为观测噪声矩阵；Zk为k时刻的观测值；Hk为观测方程矩阵。式(3)中状态噪声Wk和式(8)中量测噪声Vk的期望和协方差矩阵满足:

式中:E为数学期望符号；Qk为n×n维的半正定矩阵；Rk为m×m维正定对称阵。

式(8)中观测方程矩阵Hk满足:

(9)

式中:

hxi=(xi,k-xr,k)/r；hyi=(yi,k-yr,k)/r；

hzi=(zi,k-zr,k)/r;

r= [(xr,k-xi,k)2+(yr,k-yi,k)2+(zr,k-

zi,k)2]1/2.

2 强跟踪卡尔曼滤波器

上述已建立GPS定位系统的状态方程和观测方程。现将建立的模型应用于强跟踪卡尔曼滤波器(STKF),STKF与标准的KF相比具有以下特性[11]:① 较强的关于模型参数失配的鲁棒性； ② 较低的关于噪声及初值统计特性的敏感性； ③极强的关于突变状态的跟踪能力,并在滤波器达到稳态时保持这种能力； ④适中的计算复杂性。

一类STKF应具有如下一般结构:

(10)

(11)

(12)

Pk|k-1=λi,kΦPk-1ΦT+Qk-1,

(13)

Pk=(I-KkHk)Pk|k-1,

(14)

(15)

式中:Zk为滤波器的量测值；γk为残差序列；λk=diag[λ1,k,λ2,k,λ3,k…λ8,k]为渐消因子矩阵,分别对应 8个状态变量的渐消因子,考虑到每个状态变量的突变情况不同,当由系统的先验知识可大致确定λ1,k∶λ2,k∶λ3,k∶…∶λ8,k的初值为α=α1:α2:α3:…:α8,其中αi≥1 (i=1,2,…,8),迭代过程中, 令λi,k=αick, 其中ck为待定因子。则得到λi,k的一步近似算法:

(16)

ck=tr(Nk) r(αMk),

(17)

(18)

(19)

(20)

其中,β≥1为弱化因子,0<ρ≤1为遗忘因子。从上式可以看出渐消因子的物理意义,状态突变时,估计误差γk的增大引起误差方差阵Vk增大,λi,k渐消因子相应增大,滤波器的跟踪能力增强,使滤波器动态性能得到改善。

3 模糊自适应强跟踪卡尔曼滤波器

由上述分析可以看出, 现有强跟踪滤波器选取的都是固定弱化因子, 该固定弱化因子需依靠经验或计算机仿真来选择, 无法建立精确的数学模型。针对此问题,本文通过模糊逻辑自适应控制器与强跟踪卡尔曼滤波器的相结合, 提出了模糊自适应强跟踪卡尔曼滤波算法,该框图如图1所示。

由图1可以看出,FASTKF中的状态估计算法与STKF相同,其不同之处是通过FLAC实现了弱化因子β及次优渐消因子λi,k的“在线”自适应调整。FLAC的输入为系统的统计特征量,对特征量的隶属函数进行模糊化,然后根据模糊推理规则, 实现对β的自适应调节, 从而提高了滤波器估计精度。FLAC具体设计如下：

为监测数据的突变情况,引入残差的均值统计特征量,残差的表达式参照式(16),γk=[υ1υ2υ3…υm]T，m为可见卫星的颗数,则残差的均值满足以下式子:

(21)

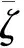
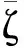
根据先验知识库得到的3条模糊推理规则,其模糊规则描述为

①IFζiszero,Thenβ=100ζ+36.

②IFζissmall,Thenβ=491.

③IFζislarge,

Thenβ=45.7 ζ2-513.9 ζ+1893.7.

FLAC输出β反模糊化方法采用重心法, 计算公式为

(22)

式中:μ为计算出的精确值；μ(ui)为隶属函数;ui为模糊集合的元素。

4 实验结果与分析

为了验证载体频繁突变场景下算法的估计性能,本文基于VC++6. 0 软件平台上, 通过GPS软件模拟器输出的数字中频信号作为信号源,设置的载体运动状态如图4所示,仿真时长为105s,在0～30s载体静止状态,30～50s载体合速度突变幅值较小,50～85s载体合速度突变幅值较大,85～105s载体匀速状态,分别用FASTKF、STKF与EKF三种方法进行仿真实验。FASTKF设置载体的初始位置、速度、钟差、钟漂为X0=[-2583646.831,4475006.977,3729132.222,…,0,0,0,0,0],P0=diag[106,106,106,106,106,106,106,106]观测量的伪矩、多普勒速度协方差分别Rρ=0.1、Rd=0.04,采样时间间隔T=0.1 s,钟差和钟漂的噪声功率谱密度取值分别为σb=0.4×10-18和σd=1.58×10-18,位置和速度的噪声功率谱密度分别为σp=10-6和σv=10-4, 初始渐消因子λi,0取值α1:α2:α3:…:α8=1:1:1:…:1,遗忘因子ρ=0.95,EKF和STKF设置的参数和FASTKF相同,其中STKF固定弱化因子β=491。

仿真结果如图5所示,图5(a)、图5(b)和图5(c)分别对应EKF、STKF 与FASTKF方法在X、Y、Z方向上的定位结果误差,在 0～13.5 s时间段内,接收机进行捕获跟踪阶段,因此无定位结果。从图中可以看出,在13.5～30 s载体静止状态,三种方法的效果近似相同,在85～105 s载体匀速状态,STKF 与FASTKF的收敛速度强于EKF。同时,可以看出在30～85 s时间段载体速度突变的情况下,STKF 与FASTKF应对载体突变的跟踪能力和收敛速度明显强于EKF,而在30～50 s中载体合速度突变幅值较小时刻,STKF 与FASTKF的滤波效果近似一样,但在50～85 s中载体合速度突变幅值较大时刻,FASTKF的跟踪性能和收敛速度强于STKF。同时从表1中可以看出,FASTKF在X方向的均方差为1.011 1,比STEKF的1.557 6和EKF的6.310 6,分别提高了84.0%和35.1%；Y方向分别提高了88.0%和44.7%；Z方向分别提高了87.9%和41.8%,总体的估计性能FASTKF明显好于STKF和EKF.

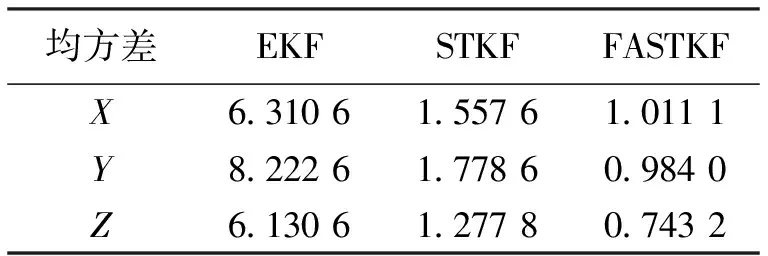
表1 EKF、STKF 与FASTKF均方差比较

5 结束语

在GPS定位解算中,提出了一种模糊自适应强跟踪卡尔曼滤波方法应用于载体状态突变,该方法将STKF中弱化因子选取与模糊自适应控制器相结合起来,实现对STKF中次优渐消因子进行自适应调整,进而实现载体突变的抑制。根据仿真实验结果表明:在没有突变的情况下,FASTKF跟踪效果和STKF、EKF一致； 在载体突变大时,FASTKF比STKF、EKF具有更强的跟踪能力,其稳定性和估计精度都有所提高。因此本文提出的FASTKF针对数据出现突变的情况,能为卫星导航定位中实时快速稳定收敛提供一定参考。

[1] 周东华,叶银忠. 现代故障诊断与容错控制[M]. 北京:清华大学出版社,2000.

[2] 夏启军,孙优贤,周春晖.渐消卡尔曼滤波器的最佳自适应算法及其应用[J].自动化学报,1990,16(3):210-216.

[3] 徐定杰,贺瑞,沈锋,等.基于新息协方差的自适应渐消卡尔曼滤波器[J].系统工程与电子术,2011,33(12):2696-2699.

[4] 杨柳庆,肖前贵,牛妍,等.基于渐消卡尔曼滤波器的定位系统设计[J].南京航空航天大学学报,2012,44(1):134-138.

[5] GENG Y, WANG J. Adaptive estimation of multiple fading factors in Kalman filter for navigation applications[J]. GPS Solutions, 2008, 12(4): 273-279.

[6] SASIADEK J Z, HARTANA P. Sensor data fusion using Kalman filter[C]//Proceedings of the Third International Conference onInformation Fusion. 2000: 19-25.

[7] 马忠孝,刘宗玉,陈明. 基于模糊逻辑的自适应卡尔曼滤波在GPS/INS组合导航中的应用[J].信息与控制,2006,35(4):457-461.

[8] 张涛,徐晓苏.基于模糊自适应的组合导航系统信息融合算法[J].中国惯性技术学报,2007,15(2):197-201.

[9] 肖志涛,赵培培,李士心.基于INS/GPS组合导航的自适应模糊卡尔曼滤波[J].中国惯性技术学报,2010,2(2):195-198.

[10] 鲁郁.GPS全球定位接收机——原理与软件实现[M].北京:电子工业出版社,2009.

[11] 周东华,席裕庚,张忠俊.一种带多重次优渐消因子的扩展卡尔曼滤波器[J].自动化学报,1991,17(6): 689-695.

Application of Adaptive Strong Tracking Kalman Filter Based on Fuzzy Logic to GPS Positioning

HU Hui1,YAN Yujun1,OU Minhui1,PENG Xiongming2

(1.SchoolofInformationEngineering,EastChinaJiaotongUniversity,Nanchang330013,China; 2.WuhanMengxinTechnologyLimitedCompany,Wuhan430073,China)

When the velocity of carrier frequently was mutated, Kalman filter have strong dependence of system model and poor robustness in GPS positioning computation. A new improved strong tracking Kalman filter based on fuzzy logic adaptive controller is presented. By monitoring the residual mean, the fuzzy logic adaptive controller of this method dynamically adjusts the softening factor according to fuzzy rules. For this reason, this method modifies the fading adaptively and achieve the inhibition of carrier mutation. The results of simulation indicate that this new approach has a better accuracy than the extended Kalman filter and strong tracking Kalman filter in the field of maneuvering target tracking in carrier mutation, its stability are also improved.

GPS； fuzzy logic adaptive controller； strong tracking filter； Kalman filter

10.13442/j.gnss.1008-9268.2017.01.002

2016-10-10

江西省自然科学基金(批准号:20142BAB207001)； 江西省教育厅科学技术研究项目(编号:GJJ14369)

P228.4

A

1008-9268(2017)01-0006-06

胡辉 (1970-),男,江西南昌人,博士,教授,主要研究方向为卫星导航定位,并行算法与并行处理,机器视觉。

颜瑜军 (1990-),男,湖南衡阳人,硕士,主要研究方向为卫星导航定位。

欧敏辉 (1990-),男,湖南株洲人,硕士,主要研究方向为卫星导航定位。

彭雄明 (1989-),男,湖北孝感人,硕士,主要研究方向为卫星导航定位。

联系人： 颜瑜军 E-mail: gnss523@163.com