采用圆弧形帆的帆船自动航行控制试验

罗潇，刘旌扬，王健，张裕芳，易宏

(上海交通大学 海洋工程国家重点实验室，上海 200240)

采用圆弧形帆的帆船自动航行控制试验

罗潇，刘旌扬，王健，张裕芳，易宏

(上海交通大学 海洋工程国家重点实验室，上海 200240)

以一艘1.2 m长的船模为试验平台，在控制程序中编入针对圆弧形风帆应用而简化改进的控制算法，分别在横风、顺风、逆风3种风况下进行模型试验,除逆风风况迎风换舷时出现异常回转，试验结果与仿真结果高度契合。针对异常回转，以提前转帆的控制策略进行改进，试验结果显示，异常回转消失，加快了换舷进程，完成了全风向自动化航行。试验证明，简化改进的控制算法结合改进的控制策略应用于圆弧形风帆可行。

实用化；自动航行；试验验证；圆弧形帆

自动化航行是指航行器通过自身系统完全自主调节运动状态从一点到达另一点的过程[1-2]。运输类帆船的智能化航行，应该结合风帆特性，以及船舶控制，找到两者之间最佳契合点，为运输类船舶加装“大脑”，实时查找出最快迫近目标点的运动状态。

圆弧形帆是运输类帆船中应用最为普遍的帆型之一，对于不同形状风帆的研究结果表明:圆弧形风帆的空气动力性能比较优良，操纵简便易行，似乎最适用于现代船舶[3]，同时标准的几何形状也为风帆制造降低了难度[4]，简单对称的外形适合船舶加装[5]。因此可以预期圆弧形帆将在智能化帆船上得到普遍应用。

针对自动化航行策略，Roland Stelzer[5]提出了一种简单有效的短途路径规划算法，算法以最快到达目标为原则，可实现全风向利用，并且引入抢风因子作为逆风航行中的换向判据，确保船舶在逆风中以“之”字形抢风航行。这是该算法的最大特点。Roland Stelzer将该算法应用于半平衡帆，效果良好。

但其在圆弧形帆上效果如何仍未可知，本文将上述算法进行简化改进，并应用于圆弧形帆船。

1 自动航行控制算法研究

1.1 最大推力系数极曲线及最佳操帆曲线

根据圆弧形风帆的空气动力学特性特定表观风向下，不同帆角所对应的艏向推力大小不同，因而存在某一特定帆角，使得该特定表观风向下的推力系数CT最大。

改变表观风向角，则可获得不同表观风向角下的最大艏向推力系数曲线。本文使用的圆弧形风帆展弦比为0.75，拱度比为0.12。经过试验测量，本文所用的圆弧形帆最大推力系数曲线绘制成极曲线，如图1所示。同时实验测量得出最佳操帆曲线，如图2所示。

可将风帆最大推力系数极曲线、最佳操帆曲线进行多项式拟合，编入算法。若绝对风向不变，自真北方向吹来，改变艏向，表观风向随之改变，则可相应获得不同艏向角下的最大推力系数极曲线。

1.2 路径规划策略

当目标点方向与船舶艏向一致，则可操纵风帆至最佳操帆角处，使得此刻艏向推力系数最大。当目标方向与船舶艏向不一致，则需从最大推力系数极曲线上循环查找，找到在船舶位置指向目标点向量——t上投影最大的推力系数。该推力系数对应的艏向即为当前最佳艏向角，在该艏向角下，船舶向目标点推进的速度最大。因此，若此刻船舶艏向不处于最佳艏向，需操舵使船舶尽快到达该艏向处。图3分别展示了顺风工况、横风工况、逆风工况下船舶所需到达的最佳艏向。

1.3 逆风工况

如图3逆风工况所示，当风从目标点方向吹来，由于最大推力系数极曲线的对称性，存在左右2个相等的最大推力系数CTL和CTR，分别对应2个最佳艏向。为了尽量缩短转向时间，优先选取距船舶当前艏向较近的最佳艏向角。船舶自动转舵使艏向到达该最佳艏向位置并航行一段时间后，CTL在t上的投影逐渐减小，CTR在t上的投影逐渐增大，如图4所示。那么，当两者差距达到何种程度时，应该将船舶艏向调换至另一侧CTR所对应的最佳艏向角处呢？为解决这一问题，引入抢风因子n，n>1，将n定义为：CTL·t与CTR·t较大者与较小者的比值。当n≫1时，则换舷频率较低，因此造成船舶航迹线宽度较大，导致短途航行的航迹线的较大偏离。当n无限接近于1时，虽然航迹线异常接近直线，但是会极大增加迎风换舷频率，船舶换舷过程所需时长较大，因此将会极大增加船舶逆风航行达到目标点的时间。经过仿真，当n为1.2时，船舶航行的航迹宽度较为合适，同时换舷频率较为合理。因此本文将n确定为1.2。仿真结果如图5所示。

1.4 控制算法流程

控制算法对于最佳艏向角的选取所需参数包括：目标点位置、船舶当前位置及姿态、风向。以上参数均通过船上传感器测量获得。算法工作的原理如下：根据当前所测表观风向角φw，先向右舷查找，以步长5°循环叠加至φw，根据式(1)计算出相应表观风向角处的推力系数，将该推力系数投影至目标向量t，投影最大的艏向，即为右侧最佳艏向；当叠加值α≥180°时，转换为左舷查找，方法类似于右舷查找。左右两侧均查找出相应的最佳艏向，再进行迎风换舷判断。

解算出当前最佳艏向后，以闭环控制操舵到达最佳艏向处，同时风帆始终处于当前表观风向对应的最佳操帆角处，保证船舶实时艏向推力最大。操帆系统与艏向控制系统为两个独立的闭环控制系统。该路径规划控制算法以2 s为周期不断循环解算，当船舶前进造成环境参数改变时，测量的数据得到实时更新。本文不考虑偏航影响。

1.5 控制算法仿真结果

对控制算法进行仿真，建立试验帆船的数学模型。单次模拟风速均匀恒定，以相同大小和方向遍布设定风场，以最大推力系数极曲线函数计算最佳艏向角，抢风因子取1.2，不考虑偏航影响。控制算法的仿真结果见图6，分为横风、顺风、逆风3种工况。

由图6可见，在横风工况下，帆船航迹如图6a)所示，在末段出现了“之”字形航迹，因为航迹末段船舶处于逆风。在顺风工况下，帆船航迹较为光顺平滑，与起止直线仅有细微偏离，见图6b)。在逆风工况下，船舶以“之”字形航迹抢风航行(见图6c))，且航迹宽度不断减小，因为船舶不断接近目标点，航行较短距离便能达到换舷节点n=1.2。

2 在圆弧形帆船上的试验验证

2.1 试验平台简介

设计试验船舶保证船舶的稳定性以及良好的操纵性，即使在较大的风力作用下，也不会发生严重横倾。选用的圆弧形帆高400 mm、宽350 mm。船控制系统由中央处理单元、传感器单元、执行器及驱动单元、通信单元4部分组成。其中惯性导航仪测量船舶姿态；风向传感器获取表观风向信息；DGPS获取船速及方位信息；帆角反馈单元实时测量帆角。岸基电脑经由5 G局域网，以远程桌面的方式访问船基主控电脑PC104， 监视船舶姿态。试验船控制系统框图见图7。

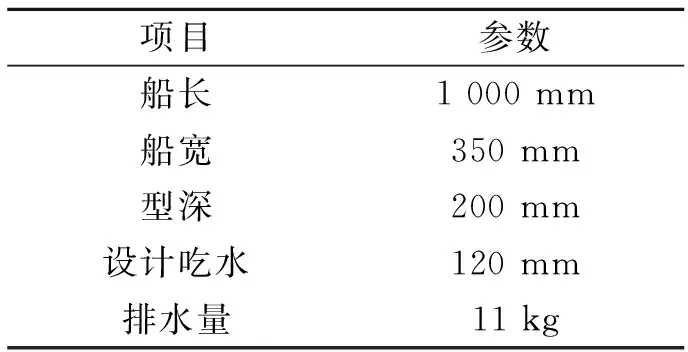
表1 试验平台主要参数

2.2 试验过程

试验地点为上海交通大学致远湖，湖面开阔，周围无高大建筑物遮挡，风情较为稳定，无湍流影响。然而自然风场并非均匀恒定，具有时变性和不均匀性，因此给试验造成了一定困难。为最大程度获得均匀恒定风场，选择风情较为稳定的天气条件进行试验，以秋季为宜。

以试验实现圆弧形硬帆船的全自动航行为目标，以时间最短为最优化原则，根据不同风向情况下风帆船航迹在算法作用下的不同预期，将试验分为3组：船舶顺风、船舶横风、船舶逆风。船舶目标点由风情决定，起点一般为船舶当前位置，偶有调整，以船舶到达距目标点0.3 m圆周内为航行结束。观察所得结果与预期结果的契合程度。

2.3 试验结果分析

航行结果分为横风试验、顺风试验、逆风试验，每一组试验数据均为同一次航行所测数据，包括表观风向角数据、帆角数据、实际艏向角数据、船舶航迹，绘制成图。

2.3.1 横风试验结果分析

横风试验见图8。由图8a)可知，实际风向大致保持在船艏偏右侧60°位置上下跳跃，整体为横风风情。对比帆角反馈数据图和船舶艏向角变化图可知，帆角变化趋势与表观风向角变化趋势相近，表明风帆持续适应风向，寻找艏向推力最大位置。该结论在顺风试验和逆风试验中也得到较好映证。船舶航迹图8d)横坐标为经度，正向指向东，纵坐标为纬度，正向指向北。由图8d)可知，在该实际风向下，船舶航迹线与仿真结果高度契合，航迹末段，船舶处于逆风情况，出现了较为明显的“之”字形航迹。

2.3.2 顺风试验结果分析

顺风试验，见图9。

由图9a)可知，表观风向前30 s大致在120°附近改变，航行中部较长的时间段内，表观风向保持在240°上下，最后50 s表观风向在270°附近，整个航行过程中，船舶都处于较为有利的顺风条件下。由图9c)可知，船舶艏向角未出现太大波动，航向较为稳定。由图9d)船舶航迹图可以看出，在有利的顺风条件下，船舶航行曲线较为平滑，高度契合算法预期结果。途中实际风向偶有微小波动，因此航迹线出现轻微波动，这是算法实时寻找最佳艏向角的结果。

2.3.3 逆风试验结果分析

逆风试验，见图10。由图10a)表观风向数据可以看出，表观风向前半段在330°附近波动，后半段左右侧交替，但均保持在船艏左右两侧60°范围，故船舶在绝大部分航行时间内，都处于逆风情况。由图10d)船舶航迹图可以看出，逆风条件下，航迹线呈现出较为完美的“之”字形，很好地契合仿真结果，然而航迹线在途中A点出现了意外回转。这是因为此时风帆处于特定帆角，圆弧形帆受到的横向力极大，方向为指向船舶左舷，该横向力针对船舶回转中心的转矩与舵升阻力提供的转矩相反，当其增大到超过舵效，便使船舶发生反向回转，出现圆形航迹。若在换舷节点A改变帆角，使横向力指向右舷，则此时横向力针对船舶回转中心的扭矩与舵效同向，不仅抑制反向回转，而且加快船舶转向。

2.4 控制策略改进及试验验证

于是增加一条转帆规则，在船舶换舷节点处，将帆角提前转至下一段稳定航迹对应的最佳帆角处，并针对绝对参考系不变，进行试验，试验结果绘图，见图11。

由图11d)船舶航迹图可知，在逆风工况下，船舶不再发生意外回转，以“之”字形航迹迫近目标点，且航迹高度契合仿真结果。

计算换舷所需时间，程序中以计算艏向和实际艏向的差值大于80°为门槛值判断是否正在换舷，从算法解算出开始换舷至换舷完成所用的时间定义为换舷时间。换舷时间长短与风速大小有关，但在较为稳定的自然风场下，风速大小对换舷时间影响不大。

对比改进前后换舷所用的平均时间(从算法解算出换舷需求至最终到达下一稳定的最佳艏向角的时间)见表2。

表2 改进前后换舷所需时间对照表 s

由表2可知，改进前单次换舷时间均在20 s以上，并且平均换舷时间为30.8 s；改进后，单次换舷时间大部分在20 s以下，平均换舷时间为19.6 s，较之前缩短了10.2 s。因此，控制策略改进极大地节约了换向时间，解决了该控制算法在圆弧形帆上的实际应用问题。

3 结论

该自动化帆船控制算法在圆弧形硬帆船上得到有效验证，并且针对圆弧形帆船迎风换舷时出现的反向回转问题，改进控制策略取得了良好效果，解决了反向回转，并且极大地节约了换舷时间。总体而言，较好地实现了圆弧形风帆船的全风向自动化航行，因此圆弧形风帆可以用该简化改进的控制算法结合改进的控制策略投入使用，作为圆弧形风帆船的实用化参考。关于后续研究，可以定位于风帆船的避碰策略，从而实现风帆船的无人化安全航行。

[1] BOWDITCH N. The american practical navigator[M]. Paradise Cay Publications，2010.

[2] STELZER R. Autonomous sailboat navigation[D]. Leicester: De Montfort University，2012.

[3] 张云彩，盛振邦.圆弧形风帆空气动力性能的试验研究[J].中国造船，1983(4)：1-10.

[4] 杨龙霞.风帆助航远洋船的翼帆性能及其机桨配合研究[D].上海：上海交通大学，2013.

[5] 林虹兆.圆弧形风帆的气动优化及双帆干扰研究[D].大连：大连海事大学，2013.

[6] STELZER R, PRÖLL T. Autonomous sailboat navigation for short course racing[J]. Elsevier journal of robotics and autonomous systems，2007，56(7)：604-614.

Experimental Research on the Control Algorithm of an Autonomous Sailboat

LUO Xiao, LIU Jing-yang, WANG Jian, ZHANG Yu-fang, YI Hong

(State Key Laboratory of Ocean Engineering, Shanghai JiaoTong University, Shanghai 200240, China)

Aims to make the autonomous circular-arc sailboat with navigation into practice experimentally. An algorithm based on the optimization of the time derivative of the distance between boat and any specified target was applied to an unmanned and autonomously controlled sailboat for verification in self-propulsion test. The navigation route agreed well with expected results, except for the wrong reverse turning in hysteresis condition. To solve the problem, the control algorithm was upgraded at the turning corner by adding a principle that trim the sail to an optimal position at the beginning of the next leg, which led to a considerable decrease of navigation time in experiments carried out later. The autonomous navigation is accomplished successfully definitely.

practicality; autonomous navigation; Experimental verification; circular-arc sailboat

10.3963/j.issn.1671-7953.2017.02.041

2016-09-08

上海交通大学海洋工程国家重点实验室自主研究课题(GKZD010061)

罗潇(1991—)，男，硕士生

U664.31；U664.82

A

1671-7953(2017)02-0175-05

修回日期：2016-10-21

研究方向:海洋运载器智能控制