异步起动永磁同步电动机起动过程中永磁体平均工作点的解析计算

唐旭， 王秀和， 徐定旺

(1.山东大学 电气工程学院，山东 济南 250061；2.青岛理工大学 自动化工程学院，山东 青岛 266520)

异步起动永磁同步电动机起动过程中永磁体平均工作点的解析计算

唐旭1,2， 王秀和1， 徐定旺1

(1.山东大学 电气工程学院，山东 济南 250061；2.青岛理工大学 自动化工程学院，山东 青岛 266520)

针对采用时步有限元法研究异步起动永磁同步电动机起动过程中永磁体工作点的变化时存在计算时间长、不适合电机设计阶段的快速计算的问题，通过将异步起动永磁同步电动机的动态数学模型和磁路计算模型结合，建立了异步起动永磁同步电动机起动过程中永磁体平均工作点的解析计算模型。利用该解析计算模型计算了3台样机起动过程中永磁体平均工作点的变化，分别得到了电机起动过程中最大退磁磁场出现时的永磁体平均工作点和电机稳定运行时的永磁体平均工作点。通过与有限元法的计算结果作比较，验证了该解析计算模型的准确性，可为该类电机的快速设计提供参考。

异步起动永磁同步电动机；动态数学模型；磁路计算模型；起动过程；平均工作点

0 引 言

异步起动永磁同步电动机在结构上可以看作是在感应电动机的转子铁心内放置了永磁体，依靠转子鼠笼产生的异步转矩实现自起动[1-2]，具有功率因数高、效率高、经济运行范围宽等优点，在高效节能场合具有广阔的应用前景[3]。

与其他类型的永磁电机一样，异步起动永磁同步电动机在实际使用过程中，当永磁体的工作点低于永磁体退磁曲线拐点时，永磁体会发生不可逆退磁[4-5]，这不仅会导致电机的反电动势减小、起动电流增大[2]，还会导致电机的效率下降，并可能产生转矩波动及振动噪声[6-7]。

在异步起动永磁同步电动机的起动过程中，定子绕组和转子鼠笼导条中的电流会产生强退磁磁场，使永磁体的工作点不断变化，可能导致永磁体发生不可逆退磁。异步起动永磁同步电动机起动过程中的永磁体退磁问题得到了广泛的研究：文献[8]利用二维有限元法计算了电机起动过程中永磁体某点磁密值的变化，并分析了永磁体退磁磁场产生的原因；文献[9]和文献[10]利用二维有限元法计算了电机起动过程中永磁体平均工作点的变化，并研究了电枢磁动势对永磁体的退磁作用以及负载条件、电源电压等因素对永磁体退磁的影响。可以看出，现有文献基本都采用时步有限元法研究异步起动永磁同步电动机起动过程中永磁体工作点的变化，尚未有文献建立电机起动过程中永磁体平均工作点的解析计算模型。

在异步起动永磁同步电动机的设计阶段，为了保证电机在实际运行中永磁体不发生不可逆退磁，需要校核永磁体的最小平均工作点(永磁体遇到最大退磁磁场时的平均工作点)，并使其不低于某一限定值。传统的计算方法所基于的假设是：电机起动至接近同步速时，转子鼠笼对转子内永磁体的屏蔽作用减弱，电枢磁动势对永磁体的去磁作用最为严重[11]；但是并不能保证在电机的实际起动过程中，永磁体的平均工作点不会低于该计算值。有限元法能够计算永磁体各点的磁密分布，可以方便的计算电机起动过程中永磁体最小工作点和平均工作点的变化；但是有限元法建模复杂、计算周期长[12-13]，不适合电机设计阶段的快速计算。

本文通过将异步起动永磁同步电动机的动态数学模型和磁路计算模型结合，建立了电机起动过程中永磁体平均工作点的解析计算模型，能够快速计算并分析起动过程中永磁体平均工作点的变化，可为该类电机的设计提供参考。本文以3台异步起动永磁同步电动机为例，在Matlab/SIMULINK中建立了相应的计算模型，计算并分析了电机起动过程中永磁体平均工作点的变化。利用有限元法验证了所建立解析计算模型的计算准确性，并得到了相应的结论。

1 起动过程中永磁体平均工作点的解析计算模型

1.1 异步起动永磁同步电动机的动态数学模型

本文建立的异步起动永磁同步电动机起动过程中永磁体平均工作点的解析计算模型主要包括电机的动态数学模型和磁路计算模型两部分。

三相静止ABC坐标系下的电机动态数学模型十分复杂，通过坐标变换(本文采用正交变换)将其变换到两相旋转dq0坐标系下，可以使方程得以简化，便于计算分析。文献[14-16]建立了异步起动永磁同步电动机在dq0坐标系下的动态数学模型，电压方程为：

(1)

式中：d轴为转子永磁磁场的轴线方向，q轴在空间超前d轴90°电角度；ud、uq分别为定子直、交轴绕组的电压；u2d、u2q分别为转子直、交轴绕组的电压；R1为定子每相绕组的电阻；R2d、R2q分别为转子直、交轴绕组的电阻；id、iq分别为定子直、交轴绕组的电流，i2d、i2q分别为转子直、交轴绕组的电流；ψd、ψq分别为定子直、交轴绕组的磁链，ψ2d、ψ2q分别为转子直、交轴绕组的磁链；ωr为电机转子旋转的电角速度。需要注意的是，上述转子各量已归算到定子侧。

磁链方程为：

(2)

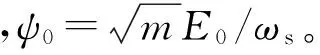
电磁转矩方程为

Tem=p(ψdid-ψqiq)。

(3)

式中p为电机的极对数。

不计铁耗和附加损耗时，机械运动方程为

(4)

式中：J为电机转子和负载的转动惯量之和；TL为负载转矩。

利用异步起动永磁同步电动机的动态数学模型，可以计算电机起动过程中各时刻的定转子直、交轴绕组电流等数据，为利用磁路计算模型计算永磁体的平均工作点奠定了基础。

1.2 异步起动永磁同步电动机的磁路计算模型

永磁电机负载时的等效磁路计算模型如图1所示[11]。其中，fc、fm、fd分别为永磁体磁动势、外磁路磁动势和等效增(去)磁磁动势的标幺值，对于异步起动永磁同步电动机，该增(去)磁磁动势是定转子绕组的直轴合成磁动势；λ0、λδ、λσ分别为永磁体内磁导、主磁路磁导和漏磁路磁导的标幺值；φm、φδ、φσ分别为永磁体、主磁路和漏磁路磁通的标幺值。为了便于与电机动态数学模型结合，本文规定，定转子绕组直轴合成磁动势起增磁作用时为正。

求解等效磁路模型，可以得到永磁体的平均工作点为

(5)

在异步起动永磁同步电动机起动过程中，根据各时刻的定转子绕组直轴合成磁动势，利用磁路计算模型，可以计算对应时刻的永磁体平均工作点。

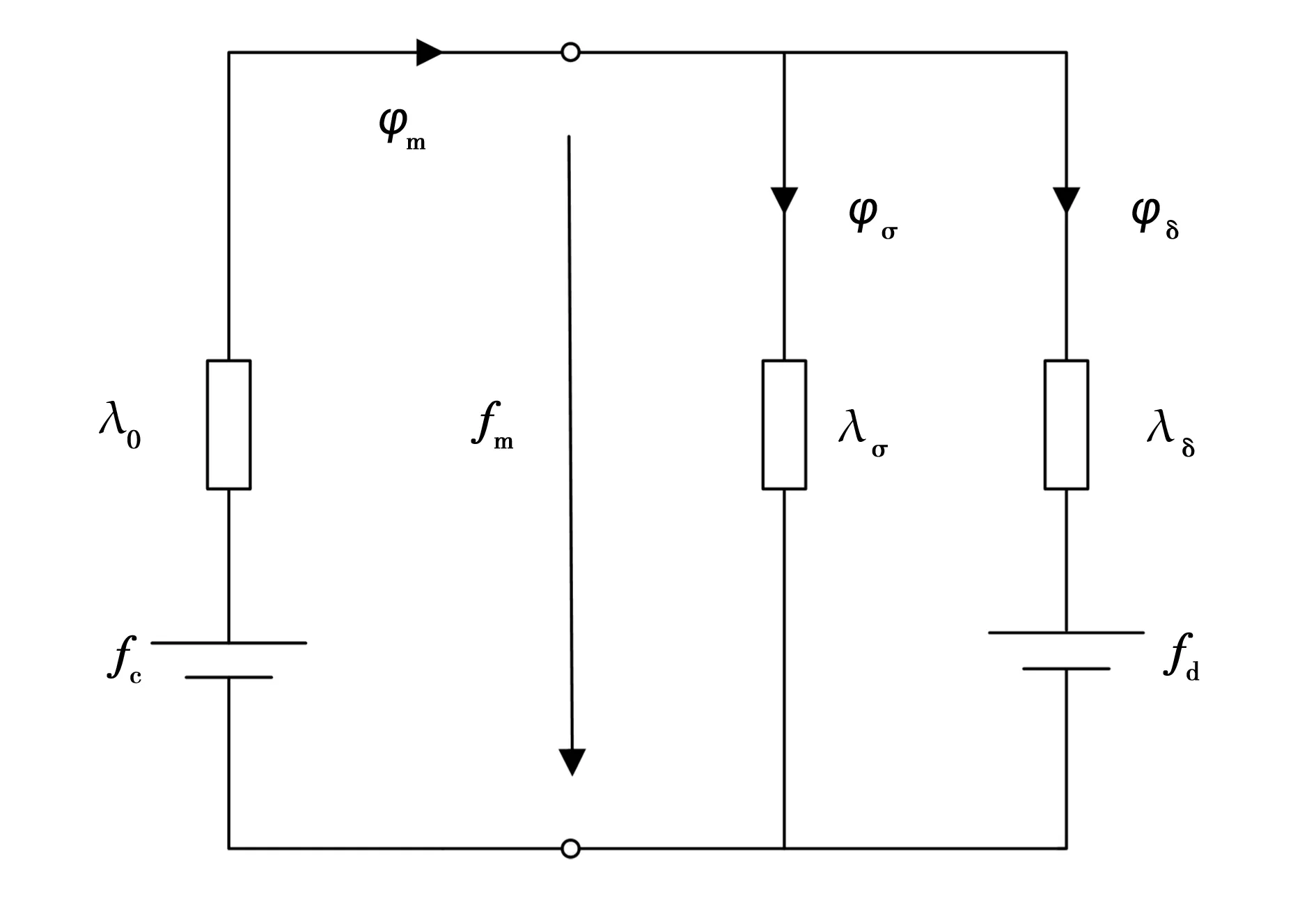
图1 永磁电机的等效磁路模型Fig.1 Magnetic circuit of permanent magnet machine

1.3 定转子直轴合成磁动势的计算

从上述分析可以看出，利用异步起动永磁同步电动机的动态数学模型可以计算出各时刻的定转子绕组直轴电流，而利用磁路模型计算永磁体平均工作点需要的是定转子直轴合成磁动势。因此，将电机的动态数学模型和磁路计算模型结合起来计算电机起动过程中永磁体平均工作点的关键是确定定转子绕组直轴电流与定转子绕组直轴合成磁动势之间的关系。本文在多相绕组合成磁动势计算公式的基础上，推导了采用正交变换时，定转子绕组直轴电流与定转子绕组直轴合成磁动势之间的关系式。

根据电机学基本原理，m相绕组的合成基波磁动势幅值为

(6)

式中：N为绕组每相串联匝数；kw1为基波磁动势的绕组因数；Iφ为相电流的有效值。对应的直轴磁动势为

(7)

式中θa为合成基波磁动势与电机直轴之间的夹角。

由于电机的直轴电流可以表示为

Id=Icosθa。

(8)

式中I为电流综合矢量的幅值。因此，式(7)可以变换为

(9)

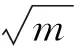
(10)

在电机动态数学模型中，转子侧参数已经归算到定子侧；因此，利用动态数学模型得到的定转子绕组的直轴电流可以计算定转子绕组的直轴合成磁动势

(11)

作用于永磁体的等效增(去)磁磁动势为

Fd=Fd1Kad。

(12)

式中Kad为直轴电枢磁动势折算系数。

1.4 起动过程中永磁体平均工作点计算模型的建立

利用上述定转子绕组直轴电流与直轴合成磁动势的关系式，通过将异步起动永磁同步电动机的动态数学模型和磁路计算模型结合，可以建立电机起动过程中永磁体平均工作点的解析计算模型，计算流程如图2所示。首先利用动态数学模型计算的各时刻定转子绕组直轴电流，由式(11)、式(12)计算出对应的等效增(去)磁磁动势，然后利用磁路计算模型计算出对应时刻的永磁体平均工作点。

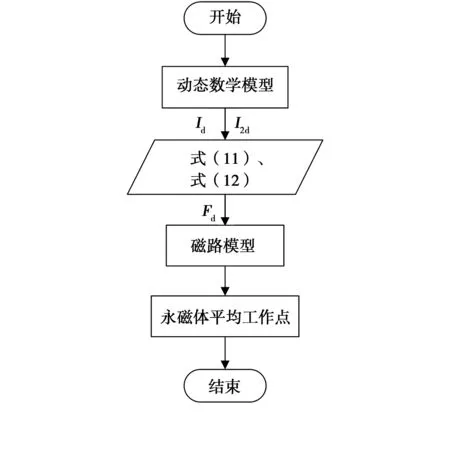
图2 计算流程图Fig.2 Flowchart of the established model

2 起动过程中永磁体平均工作点计算模型的仿真分析

2.1 仿真样机的主要参数

本文在Matlab/SIMULINK中建立了异步起动永磁同步电动机起动过程中永磁体平均工作点的解析计算模型，以3台异步起动永磁同步电动机为样机，分别计算了电机起动过程中永磁体平均工作点的变化，并利用有限元法验证了所建立模型的计算准确性。3台样机的主要设计参数和额定参数分别如表1～表6所示，其中，样机的定转子漏抗等参数是利用文献[3]中的解析方法计算得到的。

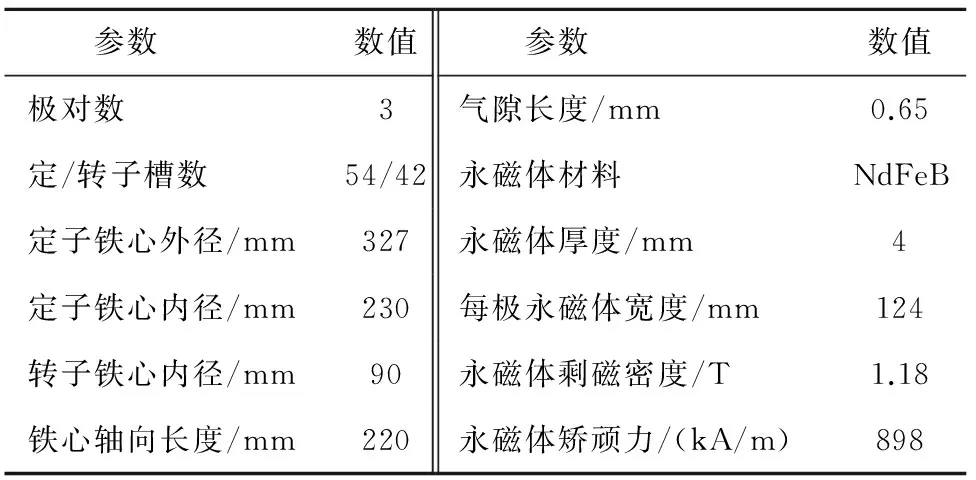
表1 样机一的主要设计参数Table 1 Design parameters of the first prototype motor

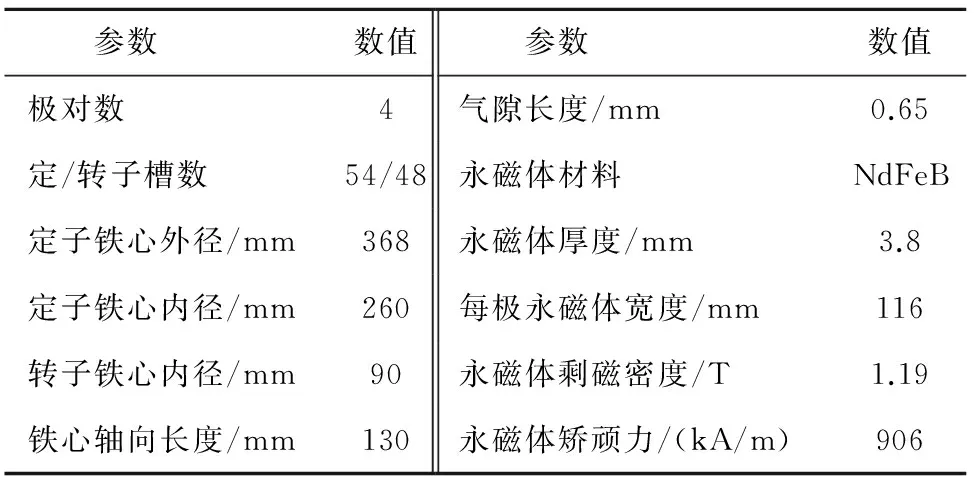
表2 样机二的主要设计参数Table 2 Design parameters of the second prototype motor

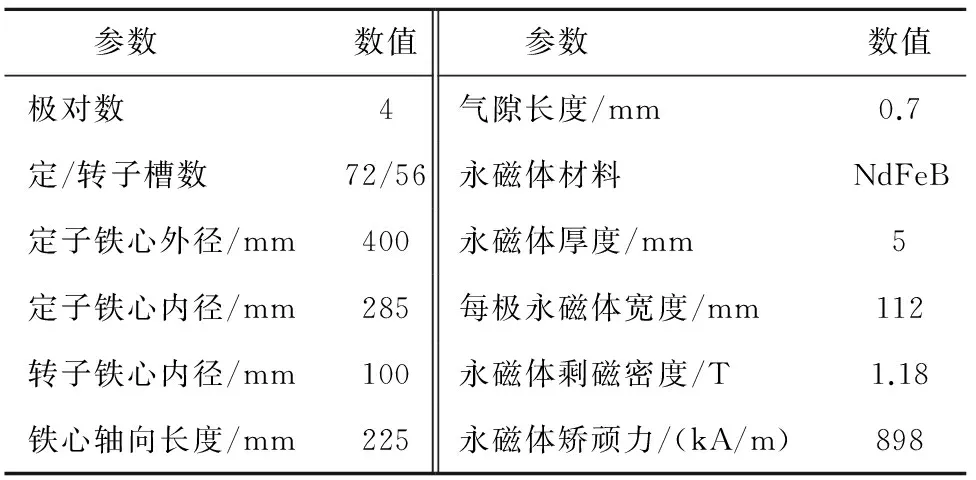
表3 样机三的主要设计参数Table 3 Design parameters of the third prototype motor

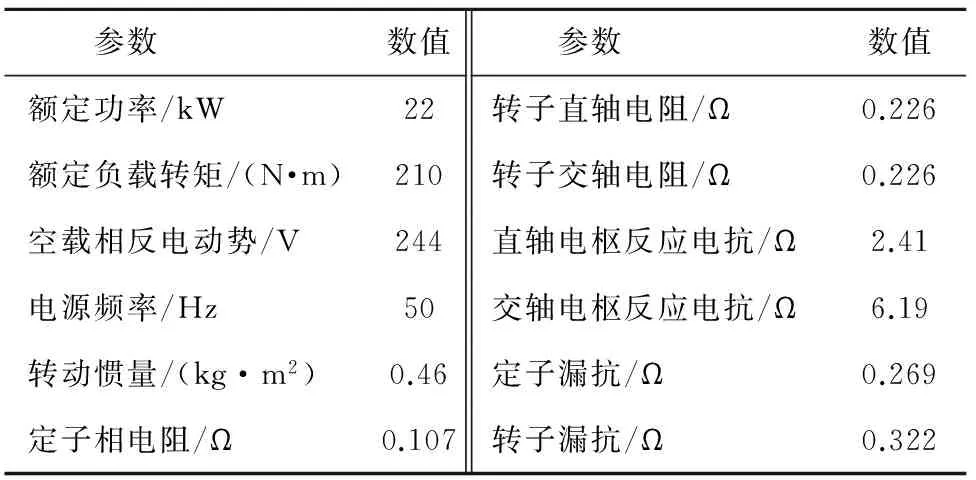
表4 样机一的主要额定参数Table 4 Rated parameters of the first prototype motor

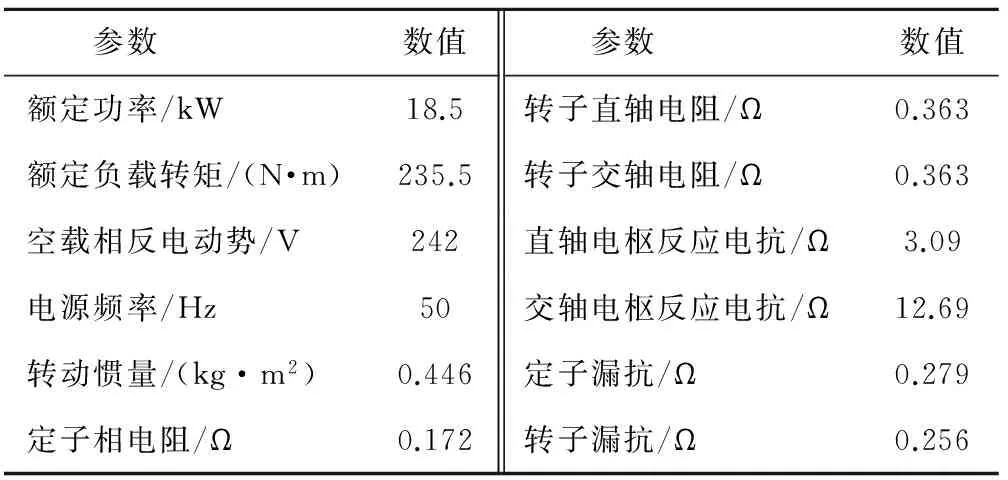
表5 样机二的主要额定参数Table 5 Rated parameters of the second prototype motor

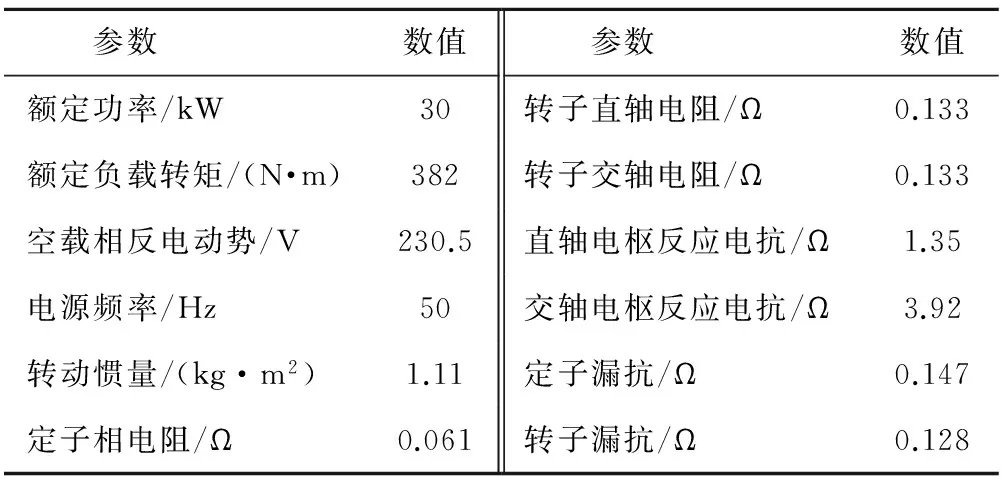
表6 样机三的主要额定参数Table 6 Rated parameters of the third prototype motor

2.2 计算准确性验证

2.2.1 永磁体最小平均工作点的计算

文献[11]指出，在异步起动永磁同步电动机的起动过程中，永磁体的最大退磁磁场出现在电机转速接近同步速时。

在Matlab/SIMULINK中，利用本文建立的模型计算电机起动过程中的永磁体最小平均工作点时，采取的方法是逐步增大电机的转动惯量直至电机不能牵入同步。对于样机一，计算得到的电机转速曲线和永磁体平均工作点曲线如图3所示。可以看出，随着电机转速的上升，永磁体平均工作点曲线不断波动，退磁磁场强度不断变化；由于电机的转动惯量过大，电机未牵入同步。最终，电机转速低于同步速小幅波动，永磁体的平均工作点曲线也随着电机转速的波动而波动，且波动幅值保持不变，最小值维持在0.13 T，对应的电机转速为988 r/min，此时的永磁体退磁磁场强度达到最大值。在该状态下，定转子绕组合成磁动势与永磁磁场轴线的相对位置周期性变化，二者之间的夹角可以是0～360°电角度之间的任意角度，因此可以找到永磁体的最小平均工作点。对于样机一，利用本文建立的模型计算得到的永磁体最小平均工作点为0.13 T。

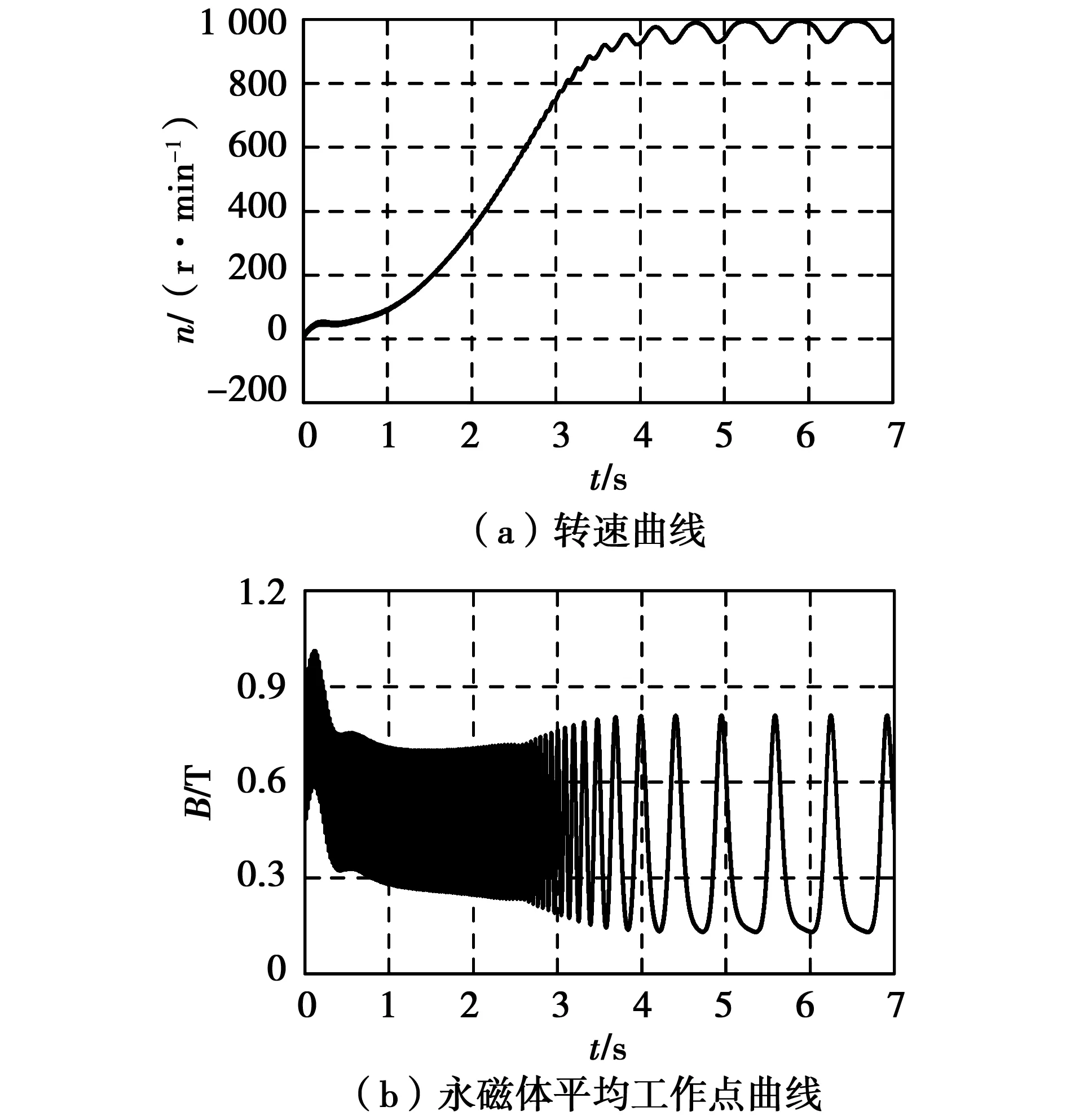
图3 转动惯量过大导致样机一不能牵入同步时的转速曲线与永磁体平均工作点曲线Fig.3 Speed and magnets′ average operating point curves during starting failure caused by large moment of inertia

在利用有限元法计算样机起动过程中的永磁体最小平均工作点时，采取相似的方法，不断增大电机的转动惯量直至电机不能牵入同步，可以得到永磁体的最小平均工作点。对于样机一，有限元法计算得到的永磁体最小平均工作点为0.11 T。

对于样机二和样机三，采用上述方法，利用本文建立的解析计算模型和有限元法可以分别计算其最小平均工作点。表7比较了利用本文建立的解析计算模型和有限元法计算得到的3台样机的最小平均工作点，可以看出，本文所建立的解析计算模型可以较准确地计算异步起动永磁同步电动机起动过程中的最小平均工作点。在电机设计阶段，本文所建立的解析计算模型可用于校验永磁体的最小平均工作点。

表7 样机的最小平均工作点比较

2.2.2 稳态时永磁体平均工作点的计算

利用Matlab/SIMULINK中建立的模型计算得到了样机一带额定负载转矩、以转子本身转动惯量起动时的转速曲线和永磁体平均工作点曲线，如图4所示。可以看出，随着电机转速的不断升高，永磁体平均工作点曲线多次波动；在a点(0.067 s)处，永磁体的平均工作点曲线出现最小值(0.169 T)，对应的电机转速为505 r/min；电机牵入同步稳定运行后，永磁体的平均工作点维持在0.742 T。

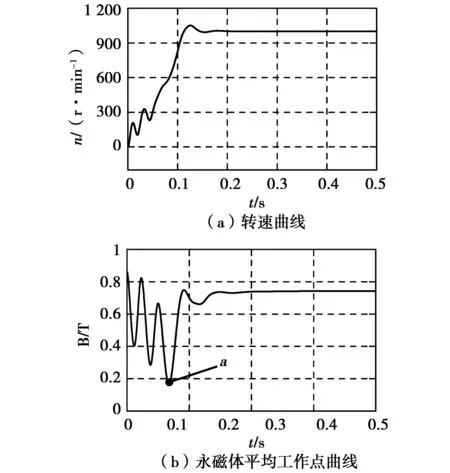
图4 样机一起动时的转速曲线与永磁体平均工作点曲线Fig.4 Speed and magnets′ average operating point curves during starting process of the first prototype motor

利用本文建立的解析计算模型分别计算了3台样机带不同负载转矩起动至稳定运行后的永磁体平均工作点，并与有限元法的计算结果作比较，结果如图5～图7所示。可以看出，解析计算结果与有限元计算结果吻合较好，本文所建立的解析计算模型可以准确地计算异步起动永磁同步电动机稳定运行时的永磁体平均工作点。

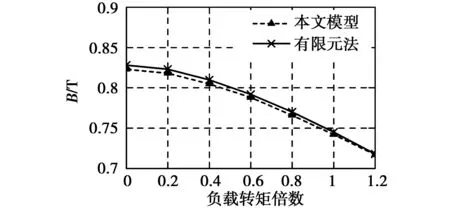
图5 样机一稳定运行时的永磁体平均工作点Fig.5 Magnets′ average operating points when the first prototype motor operates stably

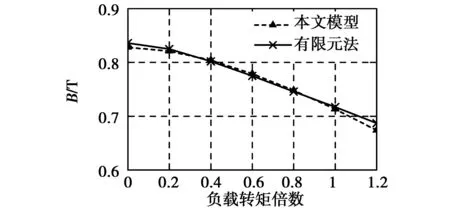
图6 样机二稳定运行时的永磁体平均工作点Fig.6 Magnets′ average operating points when the second prototype motor operates stably

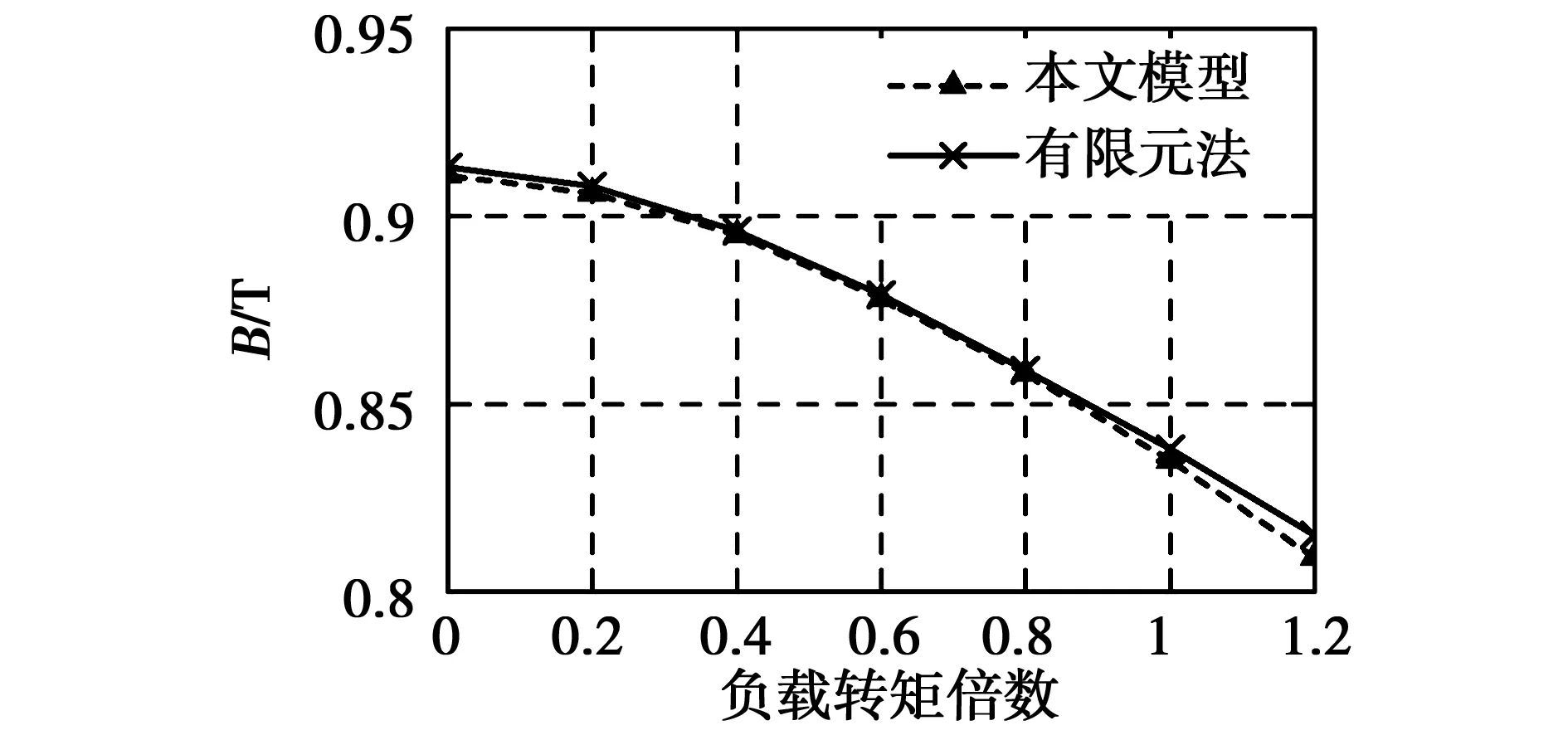
图7 样机三稳定运行时的永磁体平均工作点Fig.7 Magnets′ average operating points when the third prototype motor operates stably

2 结 论

本文通过将异步起动永磁同步电动机的动态数学模型与磁路计算模型结合，建立了电机起动过程中永磁体平均工作点的解析计算模型，并通过与有限元法的计算结果作比较验证了所建立模型的计算准确性。

结果表明，本文所建立的计算模型可以较准确地计算异步起动永磁同步电动机起动过程中的最小平均工作点和电机稳定运行时的永磁体平均工作点；该模型可为异步起动永磁同步电动机设计阶段的快速计算提供参考。

[1] KIM T H,HONG J P.A study on the irreversible magnet demagnetization in single-phase line-start permanent magnet motor[J].Journal of Applied Physics,2009,105(7): 07F108-07F108-3.

[2] KANG G H,HUR J,NAM H,et al.Analysis of irreversible magnet demagnetization in line-start motors based on the finite-element method[J].IEEE Transactions on Magnetics,2003,39(3): 1488-1491.

[3] 王秀和,杨玉波,朱常青.异步起动永磁同步电动机-理论、设计与测试[M].北京: 机械工业出版社,2009: 1-6.

[4] HONG J,HYUN D,LEE S B,et al.Automated monitoring of magnet quality for permanent magnet synchronous motors at standstill[J].IEEE Transactions on Industry Applications,2010,46(4): 1397-1405.

[5] RIBA RUIZ J R,ROSERO J A,ESPINOSA A G,et al.Detection of demagnetization faults in permanent-magnet synchronous motors under non-stationary conditions[J].IEEE Transactions on Magnetics,2009,45(7): 2961-2969.

[6] URRESTY J C,ATASHKHOOEI R,RIBA J,et al.Shaft trajectory analysis in a partially demagnetized permanent-magnet synchronous motor[J].IEEE Transactions on Industrial Electronics,2013,60 (8): 3454-3461.

[7] TORREGROSSA D,KHOOBROO A,FAHIMI B.Prediction of acoustic noise and torque pulsation in PM synchronous machines with static eccentricity and partial demagnetization using field reconstruction method[J].IEEE Transactions on Industrial Electronics,2012,59(2): 934-944.

[8] 卢伟甫,刘明基,罗应立,等.自起动永磁同步电机起动过程退磁磁场的计算与分析[J].中国电机工程学报,2011,31(15): 53-60. LU Weifu,LIU Mingji,LUO Yingli,et al.Demagnetization field analysis and calculation for line-start permanent magnet synchronous motor during start process[J].Proceedings of the CSEE,2011,31(15): 53-60.

[9] 卢伟甫,罗应立,赵海森.自起动永磁同步电机起动过程电枢反应退磁分析[J].电机与控制学报,2012,16(7): 29-33. LU Weifu,LUO Yingli,ZHAO Haisen.Armature reaction demagnetization analysis for line-start permanent magnet synchronous motor during start process[J].Proceedings of Electric Machines and Control,2012,16(7): 29-33.

[10] LU Weifu,LIU Mingji,LUO Yingli,et al.Influencing factors on the demagnetization of line-start permanent magnet synchronous motor during its starting process[C]//International Conference on Electrical Machines and Systems,August 20-23,2011,Beijing,China.2011: 1-4.

[11] 唐任远.现代永磁电机[M].北京: 机械工业出版社,2011: 185-187.

[12] FAROOQ J,SRAIRI S,DJERDIR A,et al.Use of permeance network method in the demagnetization phenomenon modeling in a permanent magnet motor[J].IEEE Transactions on Magnetics,2006,42(4): 1295-1298.

[13] WANG J,WANG W,ATALLAH K,et al.Demagnetization assessment for three-phase tubular brushless permanent-magnet machines[J].IEEE Transactions on Magnetics,2006,44(9): 2195-2203.

[14] 李国建,王道涵,朱常青.基于MATLAB/ SIMULINK的三相异步起动永磁同步电动机的建模与仿真[J].山东大学学报(工学版),2006,36(5): 40-43. LI Guojian,WANG Daohan,ZHU Changqing.Modeling and simulation of three-phase line-start permanent magnet synchronous motor[J].Journal of Shandong University (Engineering Science),2006,36(5): 40-43.

[15] 刘仲恕.永磁同步电动机状态方程研究和起动过程仿真[J].福建工程学院学报,2003,1(2): 43-46. LIU Zhongshu.On the synchronous motor state equation of permanent magnetism and emulation of starting course[J].Journal of Fujian University of Technology,2003,1(2): 43-46.

[16] WANG D H,WANG X H,CHEN H Y,et al.Matlab/Simulink-based simulation of line-start PMSM used in pump jacks[C]// IEEE Conference on Industrial Electronics and Applications,May 23-25,2007,Harbin,China.2007: 1179-1181.

[17] 王秀和,孙雨萍.电机学[M].北京: 机械工业出版社,2009: 322-334.

Analytical calculation of permanent magnets′ average operating point for line-start permanent magnet synchronous motor during starting process

TANG Xu1,2， WANG Xiu-he1， XU Ding-wang1

(1.School of Electrical Engineering,Shandong University,Jinan 250061,China;2.School of Automation Engineering,Qingdao Technological University,Qingdao 266520,China)

When finite element method (FEM) is adopted to study the variation of magnets′ operating point in line-start permanent magnet synchronous motor (LSPMSM) during the starting process,the computation is time consuming.Thus FEM is not suitable for the fast calculation at the motor design stage.To solve this problem,the analytical model to calculate the variation of magnets′ average operating point during the starting process of LSPMSM was established by combining the dynamic mathematical model and magnetic circuit model of LSPMSM.The variations of magnets′ average operating point during the starting process of three prototype motors were calculated by the above analytical model.And magnets’ average operating point when the severest demagnetization field during the starting process occurs as well as magnets’ average operating point when the motor operates stably were obtained.Accuracy of the analytical calculation model was validated by comparing with the result of FEM.Thus,the established analytical model can benefit fast design of LSPMSM.

line-start permanent magnet synchronous motor; dynamic mathematical model; magnetic circuit model; starting process; average operating point

2014-06-17

国家自然科学基金(51577107)

唐 旭(1988—)，男，博士研究生，研究方向为永磁电机； 王秀和(1967—)，男，博士，教授，博士生导师，研究方向为永磁电机； 徐定旺(1992—)，男，硕士研究生，研究方向为永磁电机。

王秀和

10.15938/j.emc.2017.05.002

TM 351

A

1007-449X(2017)05-0008-07