考虑负载不确定的异步电机反馈线性化的最小损耗控制
2017-05-15王爱元李健顾春阳
王爱元, 李健, 顾春阳
(上海电机学院 电气学院,上海 201306)
考虑负载不确定的异步电机反馈线性化的最小损耗控制
王爱元, 李健, 顾春阳
(上海电机学院 电气学院,上海 201306)
研究异步电机负载变动时基于反馈线性化的最小损耗控制的实现问题。首先分析了异步电机的损耗特性,建立了受电机温度时变参数影响小的最小损耗磁链控制模型,揭示了通过转矩的实时估计对磁链进行控制可实现最小损耗控制。应用微分几何精确线性化的理论,建立了考虑负载转矩不确定性的异步电机反馈线性化模型,实现了转速和磁链的线性化解耦控制,电机转矩的实时估计依据参考模型在电动机反馈线性化控制中实现。异步电机的反馈线性化控制既提高了动态时的响应速度,又实现了稳态时的轻载高效率运行。合理选取控制参数,实现转速、磁链以及转矩估计的渐进收敛。仿真实验表明所提控制方法的可行性和有效性。
异步电机;最小损耗;反馈线性化控制;参考模型;转矩估计
0 引 言
异步电机作为主要的用电设备,具有结构简单、坚固耐用、成本低廉、运行可靠的优点,其用电总量占世界工业用电量的60%。近年来,异步电机开始应用于伺服控制,用于改善生产工艺,实现节能,但其固有的运行特性制约了其进一步的应用。电机设计时最高运行效率在额定负载的75%左右,伺服系统对电机功率的选用要求裕量大,因此电机多工作在轻载状态时运行效率低。随着节能环保问题的日益突出,如何提高异步电机空载或轻载运行时的效率成为学术界和工程界迫切需要解决的问题。
目前,异步电机实现轻载高效率运行的基本原理是控制磁链随负载减小而下降,从而使电机的损耗下降,效率和功率因数随之提高,方法上可大体分为最小损耗模型控制[1-8]和搜索控制[9-17]。最小损耗模型控制是以精确的数学描述为基础,通过严格的实验和计算建立异步电机损耗模型,解析地求出总损耗的最小点,以最小损耗为目标控制电动机的运行。搜索控制不依赖于电动机的精确模型,依据电动机的某一运行参数如电流、功率因数等进行搜索控制。这些方法由于电机控制技术的发展联系在一起。
早期的研究,针对于标量控制相结合的节能控制有转差频率控制、压频比控制和功率因数控制[1-4,14-17],随后与矢量控制技术相结合的节能控制开始提出[5,9-13]。这些研究大多数没有考虑电机绕组电阻随温度的变化,也不能兼顾电动机的动态性能,因此在实践中也没有得到很好的应用。
近年来,也出现了与现代控制理论和智能控制理论相结合的节能控制:文献[6-8]将反步控制应用于异步电动机的节能控制;Osama S等采用人工神经网优化磁链实现了异步电机基于损耗模型的标量控制[18];Asghar Taheri等在直接转矩控制中采用自适应的梯度搜索算法实现节能控制[19];文献[20-21]将预测控制运用于电动机的动态节能控制。
本文首先建立了一种不随温度变化的最小损耗磁链控制模型,模型考虑了电动机不同的运行工况、电机的设计特点以及磁路的饱和特性,根据转矩的变化对磁链进行控制实现最小损耗;随后根据微分几何的理论建立了转速和磁链解耦的反馈线性化控制,依据模型参考的偏差系统的稳定性建立了转矩的估计模型,根据估计的转矩实现线性化反馈控制以及对磁链实施最小损耗的在线控制;最后通过仿真实验验证所提出的控制方案。
1 异步电机最小损耗分析
笼型异步电机在两相静止坐标系(α-β坐标系)下,以转子角速度、磁链和定子电流为状态变量的动态方程为:
(1)

电机的磁链和电磁转矩分别为:
(2)
(3)
稳态时,dφrα/dt=dφrβ/dt=0,由式(1)的第2个、第3个方程得:
(4)
忽略机械损耗,电机的损耗为
(5)
由式(2)~式(5),得
(6)
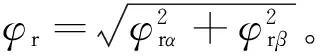
由∂p/∂φr=0,得电动机最小损耗对应的磁链为
(7)
式(7)表明,最小损耗对应的磁链与转矩和定转子绕组的电阻、电感有关。实际运行的电机,转矩是不方便也不容易测量的,但可以通过下文的基于参考模型的电动机线性化反馈控制偏差进行估计;优化的磁链小于电机的额定磁链,磁路保持线性,因此Lm和Lr保持不变;定转子绕组的电阻Rs和Rr随绕组温度的变化同时增大或减小,但其Rr/Rs保持不变。综合以上分析,最小损耗时磁链的控制关键是对转矩进行实时估计。
式(7)同时表明,最小损耗对应的磁链的平方与电磁转矩成正比;但电机受限于磁路的饱和,其磁链低于额定磁链。
通常电动机的最高效率设计在额定负载转矩的75%左右,此时电机的磁链接近额定磁链,输出转矩继续增大,磁链保持额定磁链不变。同时电机在起动、调速等动态过程中,其输出转矩往往大于额定转矩,这时磁链也要保持在额定磁链不变。因此由式(7)得到电动机转矩低于75%额定转矩时最小损耗对应的磁链,是针对电机空载或轻载时的最小损耗节能控制。因此,式(7)进一步表示为:
(8)
式(8)中最小损耗的磁链控制的转矩切换点可根据具体的电机做适当的调整。
2 输入输出线性化控制
对于式(1),重新定义状态向量
x=[x1,x2,x3,x4,x5]T=[ω,φrα,φrβ,isα,isβ]T。
(9)
输入向量为
(10)
输出向量为
(11)

(12)

按照系统输入输出反馈线性化的方法,对2个输出变量依次取高阶时间导数,直至导数中出现输入变量,得到采用李导数的表达式如下:
(13)
根据微分几何的理论,系统的相对阶为2+2=4,系统可以分为转速和磁链2个相互独立的2阶子系统,而根据式(12)系统为5阶系统,因此要实现输入输出线性化,可引入转子磁场位置角作为第3个输出变量,如下式所示:
(14)

(15)
引入非线性变换为
(16)

(17)
式(17)中的第2、第4个方程进一步表示为
(18)
式中v1、v2分别为转速和磁链幅值平方的虚拟控制输入。系统的线性化控制律为
(19)
考虑到系统(17)中z3为转子磁场的位置角属于慢时变的状态变量,与系统的转速、磁链相比短期内与系统的能量存储无关,因此在Lyapunov意义下是稳定的,系统的零动态是稳定的,可以采用输入输出线性化的控制。

3 控制器设计和基于参考模型的偏差系统
虚拟控制v1、v2重新设计如下:
(20)

控制参数k11、k12、k21、k22的选择首先要保证系统的稳定性和控制品质,其次要保证控制器不能进入饱和状态,即由式(19)、式(20)得到的电机系统的控制电压低于额定电压。
在控制作用下系统可进一步表示为:
(21)
稳态时扰动误差eτ=0,因此可以选择如下的参考模型:
(22)
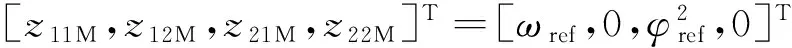
e= [e11,e12,e21,e22]T=
[z11-z11M,z12-z12M,z21-z21M,z22-z22M]T。
(23)
根据式(21)和式(22),得偏差微分方程为
Ke+Teτ。
(24)
4 系统的稳定性分析和转矩的估计
式(24)含有状态偏差和扰动偏差,可选择以下Lyapunov函数
(25)
式中:P为正定实对称矩阵;λ为适当的正实数。矩阵P同时满足KTP+PK=-Q,其中Q为正定实对称矩阵。
V沿偏差方程(24)求导数,得
(26)
注意到式(26)中(TTPe)T=eTPT,且均为标量,因此
(27)

(28)


5 仿真实验
为验证所建立的异步电机反馈线性化的最小损耗控制的有效性,首先在Matlab/SIMULINK平台上建立控制系统模型,包括异步电机、磁链观测、线性反馈控制、转矩估计、最小损耗磁链控制模块。其次对一台4kW极对数为2的异步电动机进行实验,测得主要参数如表1所示,以此作为电动机的仿真和实验的参数。
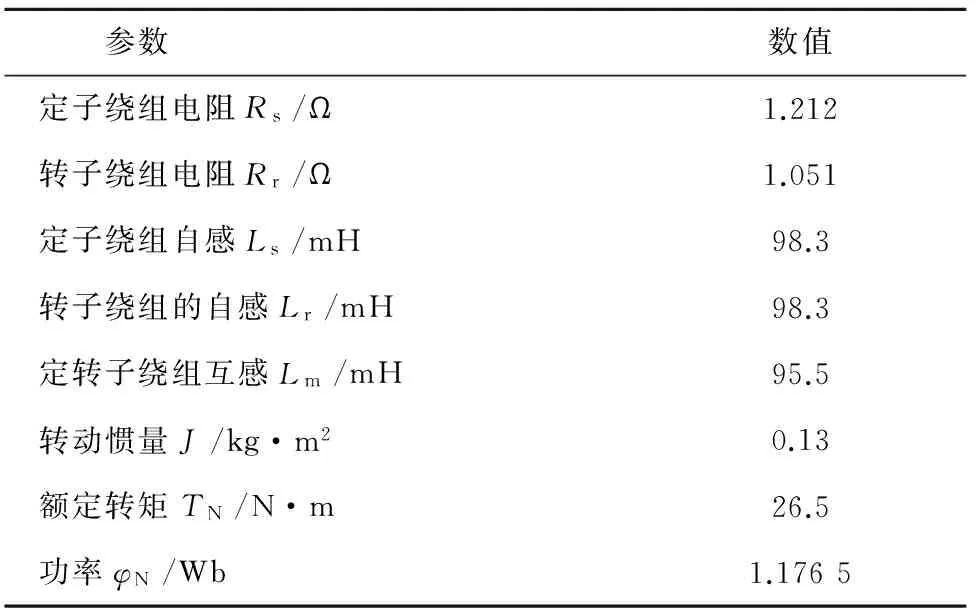
表1 异步电机的主要参数Table 1 Main parameters of induction motor
5.1 系统仿真
仿真分动态仿真和稳态仿真2个方面,动态仿真主要验证线性化反馈控制和转矩估计算法的有效性,稳态仿真主要验证电机最小损耗的控制。Lyapunov函数式(25)中与P相关联的矩阵Q取单位矩阵,λ=100。控制参数如下:
动态仿真过程如下:在0秒时刻满载起动;2秒时刻进入转速稳定状态;10秒时刻电机的负载转矩阶跃性地由TN变为0.3TN。图1、图2为动态仿真的结果。
图1为电机的输出响应及对转矩的估计,其中图1(a)、图1(b)分别为转速和磁链的跟踪曲线,图1(c)为负载转矩和估计转矩曲线。仿真表明在电机起动阶段转速和磁链均能快速地跟踪指令值,估计转矩远远高于额定负载转矩,使得磁链的指令值迅速变为额定磁链;当负载转矩在10s时刻发生突变时,转速马上有一个波动,随后又跟随转速指令,而磁链的变化要取决于估计转矩,从10.5s时刻开始估计转矩开始低于0.75TN,磁链沿式(8)确定的优化磁链曲线变化,这说明转速和磁链的跟踪控制是独立的。

图1 电机的输出响应及对转矩的估计Fig.1 Output response and estimated torque
图2为负载转矩变化前后估计转矩、磁链和损耗的变化曲线,表明当估计的转矩低于0.75TN时,磁链开始向额定磁链以下调节;而对应的损耗在负载转矩发生变化的10s时刻就开始下降,这是由于负载转矩向下调节,转速指令没有变化,输入电机的电能有所下降使得损耗有所下降。随着磁链向下调节,损耗加速下降。

图2 负载转矩变化时估计转矩、磁链和损耗的变化曲线Fig.2 Varied curves of estimated torque,flux and loss with load torque
图1、图2的仿真还表明在转速和磁链子系统取相同控制参数的情况下,转速的超调要大于磁链的超调,这是由于转矩估计的适应律式(28)与转速子系统式(18)的第1个方程还存在一定的耦合;但这不影响最小损耗的控制。
稳态仿真针对于电机带低于额定负载的转矩在优化磁链控制下稳态长期运行,并与保持额定磁链控制时的损耗进行比较。图3给出了2种磁链控制方式在电机额定转速运行时的比较。仿真表明最小损耗的优化磁链控制节能效果要优于恒定的额定磁链,特别是负载转矩低于0.3TN。随着负载转矩的增大,两种磁链控制的损耗趋于一致。
5.2 实验
以DSPTMS320F28335为控制核心搭建实验系统,1台4kW的直流发电机作为异步电动机的负载,负载的调节通过直流发电机外接的变阻器实现,电动机上安装增量式旋转编码器用于测量转速,通过霍尔电流传感器测量输入电动机的电流,通过分压滤波对输入电动机的电压进行测量,通过对测量的电压、电流进行适当运算得到电动机的输入功率和转子磁链的观测。

图3 优化磁链控制和恒定额定磁通控制的损耗比较Fig.3 Loss comparison of optimized flux and rated flux
图4为额定转速下负载转矩由0.8TN变为0.3TN时转速、磁链、估计转矩和损耗的变化曲线。实验表明:随着转矩的下降,转速有1个向上波动的变化过程,随后趋于平稳;磁链的变化随着估计转矩的下降向下调节,而当估计的转矩趋于负载转矩时,电机的运行趋于稳态,磁链也不再向下调节;损耗先有1个急剧的下降,随着转速的稳定和磁链调节的结束,损耗保持为1个小的多的数值。负载转矩变化时转速、磁链、估计转矩和损耗的变化与仿真的结果基本一致。
图5为电机电动机额定转速下带不同的负载转矩稳态运行时的实验损耗与仿真所得损耗的比较。仿真实验表明电动机所带负载转矩低于额定负载转矩时,最小损耗的磁链优化损耗明显低于额定磁链损耗,并且负载转矩越小,节能效果越显著。
通过对实验与仿真的损耗比较也能发现,实验损耗要高于仿真损耗,且负载转矩越小其差距越明显,这是因为为了简化分析最小损耗磁链优化模型以及线性化反馈控制模型都忽略了空载机械损耗和等效铁耗,式(8)是基于最小损耗的定转子铜耗的磁链优化控制,没有考虑等效的铁耗电阻;但即使这样轻载时优化的磁链要低于额定磁链,根据电机学的理论,铁耗也会相应下降,因此总损耗也是下降的,这与前人的研究[5-14]结论是一致的。
鉴于现阶段电动机空载机械损耗和等效铁耗的准确测量和计算还是比较困难的,最小损耗和转速控制忽略这2种损耗也是一种简洁有效的方法。

图4 实验获得的转速、磁链、估计转矩和损耗随负载转矩的变化曲线Fig.4 Experimental varied curves of speed,estimated torque,flux and loss with load torque
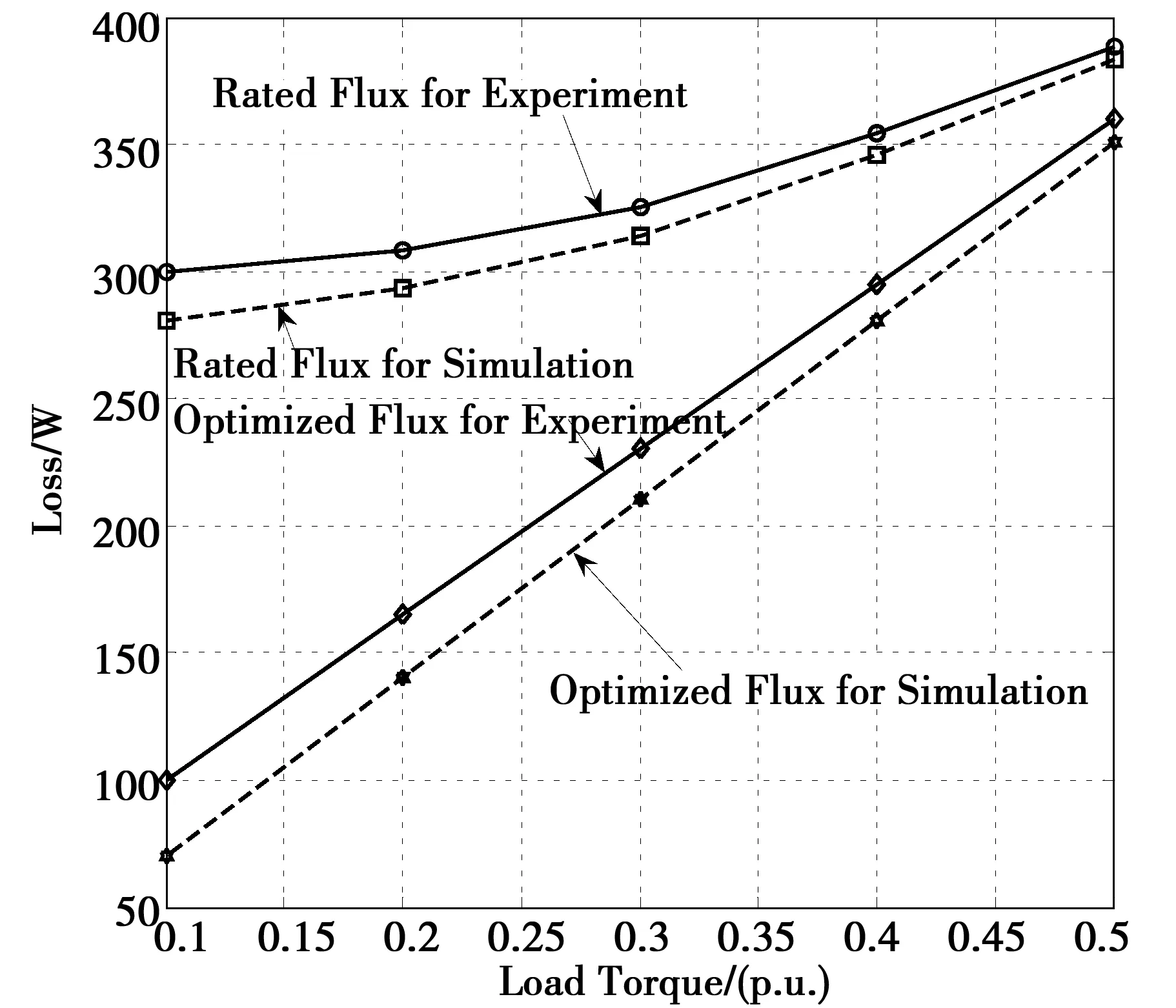
图5 实验与仿真的损耗比较Fig.5 Loss comparisons for experiment and simulation
6 结 论
本文建立了考虑磁路饱和、受温度等时变参数影响小的异步电机最小损耗磁链控制模型以及反馈线性化控制模型,采用基于参考模型的偏差系统实现电磁转矩的估计,根据估计的转矩实现最小损耗控制和线性化的反馈控制,仿真实验表明:
1)线性化反馈控制实现了转速、磁链的独立线性反馈控制;
2)电磁转矩的估计能够准确反映电动机的动态和负载转矩的变化;
3)负载转矩下降时,节能效果明显优于恒磁通控制。
未来的工作是促进最小损耗和线性化反馈控制的工程化,进一步研究考虑空载机械损耗和铁耗的最小损耗控制。
[1] KIRSCHEN Daniel S,NOVOTNY Donald W,SUWANWISOOT Warin.Minimizing induction motor losses by excitation control in variable frequency drive[J].IEEE Transaction on Industry Applications,1984,20(5): 1244-1250.
[2] 李阳,张曾科,常进.基于转差率的感应电机最优效率控制[J].电机与控制学报,2005,9(3):215-217. LI Yang,ZHANG Zengke,CHANG Jin.Slip frequency based optimal efficiency control of induction motor[J].Electric Machines and Control,2005,9(3):215-217.
[3] Andersen H R,Pedersen J K.Low cost energy optimized control strategy for a variable speed three-phase induction motor[C].IEEE Power Electronics Specialists Conference,1996,1: 920-924.
[4] 常进, 张曾科.感应电机恒功率因数控制的研究[J].中国电机工程学报,2002,22(11):70-74. CHANG Jin,ZHANG Zengke.The research on constant power factor control of induction motor[J].Proceedings of the Chinese Society for Electrical Engineering,2002,22(11):70-74.
[5] UDDIN M Nasir,SANG Woo Nam.New Online loss-minimization-based control of an induction motor drive[J].IEEE Transactions on Power Electronics,2008,23(2): 926-933.
[6] UDDIN M Nasir,SANG Woo Nam.Development of a Nonlinear and model-based online loss minimization control of an im drive[J].IEEE Transactions on Energy Conversion,2008,23(4):1015-1024.
[7] HAJIANM,SOLTANI J,MARKADEH G A,et al.Adaptive nonlinear direct torque control of sensorless im drives with efficiency optimization[J].IEEE Transactions on Industrial Electronics,2010,57(3):975-985.
[8] 苗敬利,李华德,胡广大,等.感应电机效率优化的自适应反步控制研究[J].电机与控制学报,2009,13(9):749-753. MIAO Jingli,LI Huade,HU Guangda,et al.Efficiency optimization control of induction motors based on adaptive backstepping method[J].Electric Machines and Control,2009,13(9):749-753.
[9] SOUSA Gilberto C D,BOSE Bimal K,CLELAND John G.Fuzzy logic based on-line efficiency optimization control of an indirect vector-controlled induction motor drive[J].IEEE Transactions on Industrial Electronics,1995,42(2):192-198.
[10] BOSE B K,PATAL N R,RAJASHEKARA K.A neuro-fuzzy-based on-Line efficiency optimization control of a stator flux-oriented direct vector-controlled induction motor drive[J].IEEE Transactions on Industrial Electronics,1997,44(2):270-273.
[11] ABDINE S,GHONEEM G A,DIAB H M M,et al. Efficiency optimization of a vector controlled induction motor drive using an artificial neural network[C].The 29th Annual Conference of the IEEE on Industrial Electronics Society,2003,3: 2543-2548.
[12] 刘小虎,谢顺依,郑力捷.一种改进的感应电机最大效率控制技术研究[J].中国电机工程学报,2005,25(6): 95-98. LIU Xiaohu,XIE Shunyi,ZHENG Lijie.Improvement of efficiency-optimization control of induction motor drives [J].Proceedings of the CSEE,2005,25(6): 95-98.
[13] 张立伟,温旭辉,郑琼林.异步电机用混合式模糊搜索效率优化控制研究[J].中国电机工程学报,2007,27(27): 83-87. ZHANG Liwei,WEN Xuhui,ZHENG Qionglin.Fuzzy logic based hybrid search control strategy for efficiency optimization control of induction motors[J].Proceedings of the CSEE,2007,27(27): 83-87.
[14] KIRSCHEN D S,NOVOTNY D W,LIPO T A.On-line efficiency optimization of a variable frequency induction moter drive[J].IEEE Transaction on Industry Applications,1985,IA-21(4): 610-615.
[15] KIRSCHEN D S,NOVOTNY D W,LIPO T A.Optimal efficiency control of an induction motor drive[J].IEEE Transactions Energy Conversion,1987,2(3): 70-76.
[16] SULS K,PARK M H.A novel technique for optimal efficiency control of a current-source inverter-fed induction motor[J].IEEE Transactions on Power Electronics,1988,3(2):192-199.
[17] KIOSKERIDIS I,MARGARIS N.Loss minimization in scalar-controlled induction motor drives with search controllers[J].IEEE Transactions on Power Electronics,1996,11(2): 213-220.
[18] EBRAHIM Osama S,BADR Mohamed A,ELGENDY Ali S,et al.Ann-based optimal energy control of induction motor drive in pumping applications[J].IEEE Transactions on Energy Conversion,2010,25(3): 652-660.
[19] TAHERI Asghar,RAHMATI Abdolreza,KABOLI Shahriyar.Efficiency Improvement in DTC of Six-Phase Induction machine by adaptive gradient descent of flux[J].IEEE Transactions on Power Electronics,2012,27(3): 1552-1562.
[20] STUMPER Jean-Francois,DöTLINGER Alexander,KENNEL Ralph.Loss minimization of induction machines in dynamic operation[J].IEEE Transactions on Energy Conversion,2013,28(3):726-735.
[21] VARGAS René,RODRIGUEZ Jose,ROJAS Christian A,et al.Predictive control of an induction machine fed by a matrix converter with increased efficiency and reduced common-mode voltage[J].IEEE Transactions on Energy Conversion,2014,29(2): 473-485.
Developing loss minimization of induction motors based on feedback linearization control considering load uncertainties
WANG Ai-yuan, LI Jian, GU Chun-yang
(School of Electric Engineering,Shanghai Dianji University,Shanghai 201306,China)
The research is about the loss minimization for variable load torque of induction motors with feedback linearization control.Flux control model for minimal loss without affection by time-varying parameters was deduced.Loss minimization of the motors was achieved by adjusting the flux according the torque variety.Based on exact linearization of differential geometry theory,the model of feedback linearization control considering torque disturbance was presented.The speed and the flux can be decoupling controlled in linearization.The motor torque was estimated online by reference model of the feedback linearization control.The feedback linearization control for induction motors increase dynamic response ability,as well as high efficiency operating at light loads.The speed,flux and estimated torque can realize asymptotic convergence with reasonable control parameters.The simulation and experiment results verify the feasibility and effectiveness of the proposed scheme.
induction motors; loss minimization; feedback linearization control; reference model; torque estimated
2015-10-14
国家自然科学基金(61374136);上海电机学院登峰学科建设(15DFXK01)
王爱元(1968—),男,博士,副教授,研究方向为电动机节能、新型电机及其控制; 李 健(1991—),男,硕士研究生,研究方向为新型电机设计与控制; 顾春阳(1988—),男,硕士研究生,研究方向为电机与电器控制。
王爱元
10.15938/j.emc.2017.05.010
TM 34
A
1007-449X(2017)05-0073-08
