自起动永磁同步电机转子铜耗分析的时步有限元优化离散策略

胡笳， 谷君， 奚林根， 吕克启

(1.中国电力国际有限公司，北京 100080；2.国家电网北京市电力科学研究院，北京 100075)

自起动永磁同步电机转子铜耗分析的时步有限元优化离散策略

胡笳1， 谷君2， 奚林根1， 吕克启1

(1.中国电力国际有限公司，北京 100080；2.国家电网北京市电力科学研究院，北京 100075)

利用时步有限元方法对永磁同步电机进行转子铜耗分析计算时，由于空间中高次谐波磁场的作用，使得导条中的电流与损耗在集肤效应的影响下呈非均匀分布，于是有限元模性的空间离散方案将直接对计算精度产生影响。首先通过理论推导得出导条电流密度的解析表达式；在此基础上，通过建立不同形式的目标函数，研究等间距与不等间距条件下离散密度对于损耗计算精度的影响，及其所对应的最优离散方案；最后，针对转子实际槽形结构，在考虑交界面处强制引入节点的约束条件下，提出了采用分区域循环引用最优离散点的方法，求解全局优化离散策略。通过与时步有限元计算结果进行对比，验证了方法的合理性。

时步有限元；同步电动机；损耗分析；空间离散；谐波

0 引 言

永磁式同步电动机以其高效率、高功率因数等优势逐渐成为高效节能电机的重要发展方向。该类电机在稳态运行过程中，由于空间中存在的高次谐波磁场，使得即使转子以同步速旋转，导条上亦会产生感应电流与损耗，并且在集肤效应的作用下呈非均匀分布[1-4]。

场路耦合时步有限元方法能够适用于磁场饱和、畸变，以及涡流集肤效应等多种因素的情况，实现电机转子谐波铜耗的精确分析计算。该方法计算结果的准确度与模型的空间离散密度有直接关系，过于稀疏的离散将导致计算结果与实际损耗产生严重的偏差；然而一味的细化剖分，会使得计算量与仿真时间大幅增长，并且在一定的剖分密度下，进一步增加离散密度，将不再对计算精度产生贡献。

本文在参考文献[5-7]的基础上，通过理论推导得出导条中电流密度的解析表达式，并与时步有限元计算结果进行对比，结果显示两者具有很强的一致性，证明了方法的合理性以及时步有限元计算的准确性。在此基础上，分别构造不同形式的目标函数，并通过求解隐函数所对应的非线性方程组，得出导条谐波损耗的计算精度与空间离散密度之间的关系，以及在不等间距离散情况下的最优离散策略。最后，针对转子实际槽形结构，考虑交界面处强制引入节点的约束条件，提出了采用分区域循环引用最优离散点的方法，求解全局的优化离散策略。

1 场路耦合时步有限元

以一台55 kW永磁同步电动机作为分析算例，模型如图1所示。在基本假设条件下[8-10]，通过麦克斯韦方程组得到求解区域的电磁场基本方程[11-12]如下：

(1)

式中：Ω、Γ1、Γ2分别为电机求解区域、定子外圆边界、以及永磁体边界；A为矢量磁位轴向分量；J为总电流密度；Js为永磁体边界等效面电流密度[13-14]。式(1)经有限元离散，并耦合定、转子电路方程可得场路耦合时步有限元方程如下：

(2)

其中各状态变量A、Is、Ur、Ir、P1、P2，以及系数矩阵C11…D44的具体表达式参见文献[15]。采用后差分欧拉法对式(2)进行离散[16-17]，并通过求解非线性代数方程组，可得各时刻磁场与电流结果。在此基础上，由式(3)得到转子导条电流密度为

(3)

及损耗密度[18-19]pcu=ρJ2。

图1 永磁同步电机时步有限元计算模型Fig.1 T-S FEM model of PMSM

2 解析分析

在理想假设条件下μfe=∞，根据磁场分界面条件[5-6]，磁力线将水平地穿过转子槽，而在实际的电机运行过程中，由于受到磁场饱和等因素的影响，磁力线在穿越转子导体时，将可能在局部出现不平行的现象；但通过大量的计算发现，该现象的程度往往很小。如图2所示为电机稳态运行一个周期过程中，转子导条内磁位的分布及变化情况。可见，转子导条各个时刻的磁场均近似呈水平分布特性，仅在最上层槽口部位有很小的畸变(磁位相差约0.3%)，从而在对转子导条电流密度及磁场进行解析分析时，可认为磁场强度H仅为y的函数，即H=Hx(y)(通过2.2节的解析解与时步有限元计算结果对比，可进一步证明该假设合理性)。

同步电动机转子槽形的结构复杂多样，以图3所示3类比较典型的结构进行研究，其中图3(a)所示为理想的矩形槽形，图3(b)为所采用的计算模型结构，图3(c)所示为在交界面处截面积发生突变的情况(文献[5]还针对空心槽以及半闭口槽中的磁场解析表达式进行了推导)。

图2 稳态运行过程中转子导条磁位分布Fig.2 Magnetic potential distribution in rotor bar undering steady-state operation

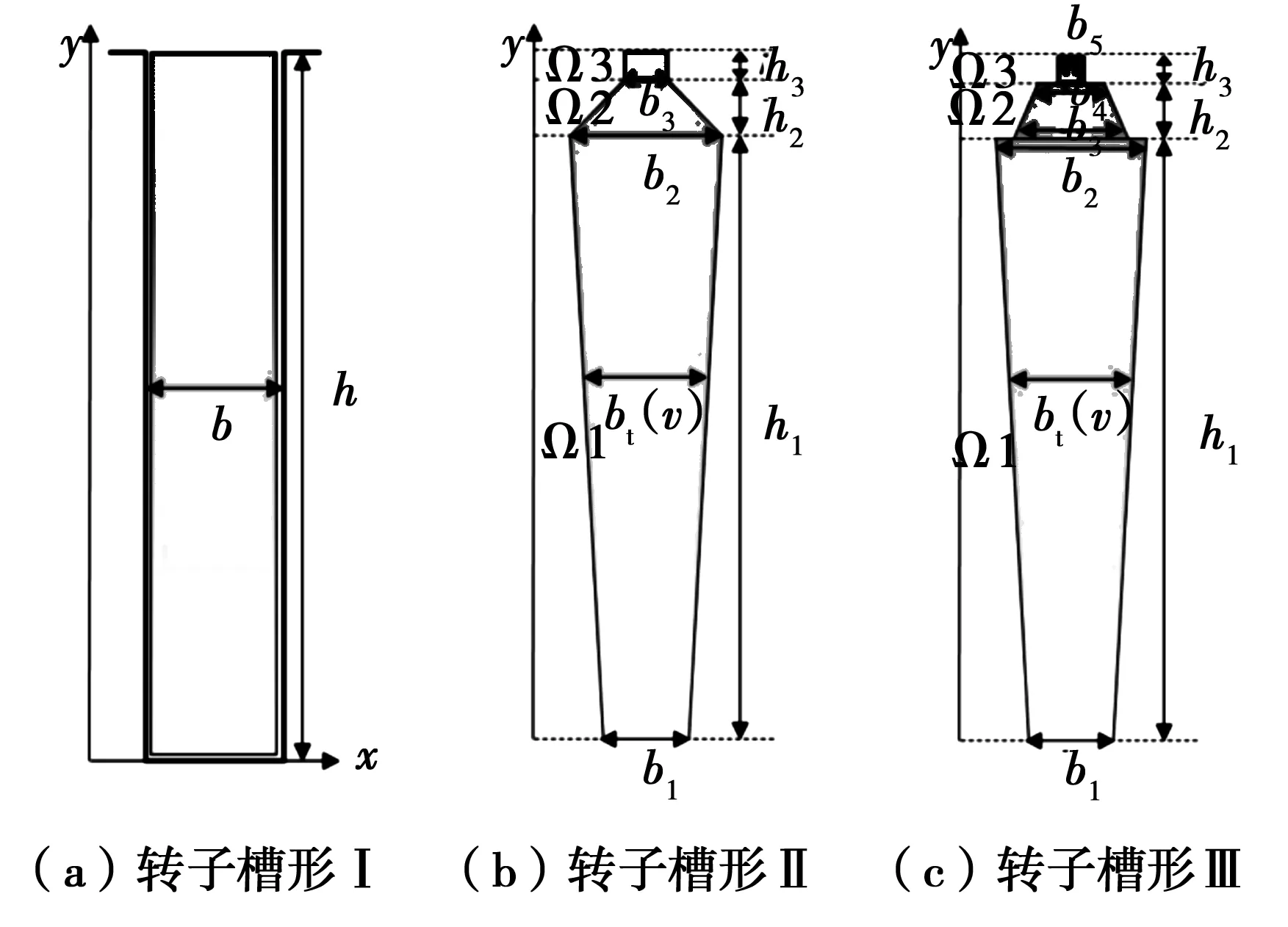
图3 转子导条模型Fig.3 Model of rotor bar

2.1 理想槽形

在图3(a)所示转子导条为矩形的情况下，对于正弦电磁场情况，由麦克斯韦方程组可得：

(4)

联立该方程组得到

∂2Hx/∂y2=jωγμ0Hx。

(5)

式(5)的解为

Hx=W1ch(py)+W2sh(py)。

(6)

(7)

将W1=0，W2=Im/bsh(ph)代入式(6)，最终得到：

(8)

利用式(8)求得导条电流密度分布如图4所示，其中Im=1 A，ω=3 600π rad/s，h=0.031 75 m，b=6×10-3m。

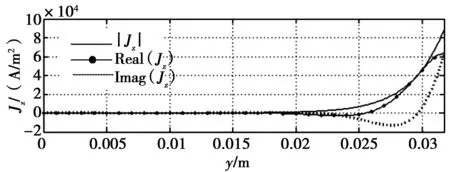
图4 导条电流密度分布Fig.4 Current density distribution in rotor bar

|Jz|、Real(Jz)、Imag(Jz)分别表示Jz的模、实部与虚部。其中|Jz|在y=0～h范围内具有单调恒正且为凹函数的特性，而Real(Jz)与Imag(Jz)不具备该特点。

2.2 实际槽形

实际运行的同步电动机，转子导条结构往往如图3(b)所示，对于该结构的转子导条，根据电磁场基本方程组[5]可以得到

(9)

联立该方程组可得：

(10)

其中bt(y)在不同区域分别为：

(11)

将式(11)代入式(10)，并令hΩ1=b1h1/(b2-b1)，hΩ2=b2h2/(b3-b2)-h1，可得：

(12)

式(12)的解为：

(13)

(14)

最终可得：

(15)

式中J1与H1分别为一阶贝塞尔函数与一阶汉克尔函数，求解方程组(15)可得待定系数W1～W6。将W1～W6代入方程(13)，最终得到该槽形结构下电流密度解析表达式。

图5所示为永磁同步电机转子导条中电流密度幅值的解析解与时步有限元计算的对比结果，其中h1=0.029 31 m，h2=0.001 44 m，h3=0.001 m，b1=4.3×10-3m，b2=6×10-3m，b3=1×10-3m。由图可见，2种方法所得结果具有很高的一致性(为实现相同条件下的对比，解析结果中的Im取自时步有限元计算值)。另外，虽然导条顶部截面积很小，但由于此处集肤效应十分明显，使得该部分对导条中总电流的作用不可忽略。

图5 导条电流密度幅值的解析解与时步有限元对比Fig.5 Comparison between analytical and T-S FEM calculating

图6所示为时步有限元计算所得的，同步电机稳态运行过程中，转子导条6次谐波电流密度的分布情况。

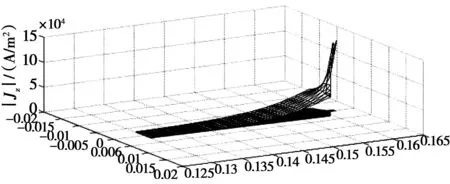
图6 导条中6次谐波电流密度分布特性Fig.6 Current density distribution of 6th harmonic content by using T-S FEM

对于图3(c)所示，分界面处导条截面积不连续的槽形情况，分界面处有的边界条件应满足：

(16)

其他分析步骤同上。

3 离散策略

在得到转子导条电流密度分布的基础上，令Jm(y)=|Jz|，导条内损耗可由式(17)表示，其中i表示导条不同区域部分。

(17)

分别取F=PΩ作为目标函数，F*表示采用离散数值积分方法所得F的近似解。从而空间离散密度对于计算精度的影响可转化为对于目标函数F的误差分析问题[20-21]，如下式所示：

(18)

3.1 等间距离散

(19)

针对图3(a)所示矩形槽结构有：

(20)

图3(b)所示转子槽形结构可由下式表示：

(21)

其中Jm1(y)、Jm2(y)、Jm3(y)、bt1(y)、bt2(y)、bt3(y)分别可由式(13)与式(11)得到。

将式(20)代入式(18)，得到不同谐波情况下转子导条损耗的计算误差随空间离散密度变化的规律曲线族(针对图3(a)结构)，如图7所示。

图7 损耗计算精度随离散点变化规律曲线族Fig.7 Variation between loss computation accuracy and discrete points

可见，计算误差随离散点数的增加而减少，且随着谐波次数的增高，达到相同的误差水平所需的离散点数也逐渐增多。例如，若要将转子导条中36次谐波损耗的计算误差控制在10%以内，沿导条径向至少需要20个等距的离散点。

3.2 不等间距优化离散

等间距离散的优点在于其方法简单，对函数性质的依赖性不强，大多数的目标函数均可十分方便的实现。然而，其显然不是最优的离散策略，即对于相同的离散点数其计算精度不是最佳的，下面针对不等间距的离散策略进行研究。

假设求解区间y=0～h分为N份，由于Jm(y)在求解区域单调恒正且为凹函数，所以F*>F，利用该性质构造目标函数G=F*-F，如下式所示：

(22)

于是最优离散策略的研究等价于求取函数G最小值的问题。

将式(22)分别对yj|j=1…N求偏导并令其等于0，将得到1个N阶非线性方程组如下：

(23)

该方程组的解y1,…,yN即为采用不等间距方式离散所得的最优离散点。将式(23)进行如下变换：

(24)

使其显性化，并以矩阵形式表示为H(Y)·Y=0。

利用牛顿-拉夫逊方法对该方程组进行求解：

Y(n+1)=Y(n)-Joc(Y(n))-1·H(Y(n))·Y(n)。

(25)

最终可得到各优化后的离散点yj|j=1…N(Joc为方程所对应的雅各比矩阵)。图8所示为转子矩形槽结构下，针对不同次数谐波损耗的优化离散方案结果。

图8 转子导条最优离散方案Fig.8 Optimal discretization method of rotor bar

图9为在不等间距优化离散方案下，不同次数的转子谐波损耗误差随空间离散密度变化的规律曲线族。

可见采用不等间距的优化离散方案进行计算时，所得到的精度较之等间距方法有大幅提高；而且，由于针对不同次数的谐波计算其离散策略不同，使得误差曲线在不同谐波情况下逐渐趋于一致。

在实际的分析中，导条中电流的各次谐波分量是共同存在的，离散方案的选择应以其中主导因素来确定，或根据其各自所占的权重比例进行加权计算，得出全局最优函数。另外，由于该方法的计算量相对较大，且受目标函数具体表达式的影响，若其形式过于复杂，在求解非线性方程组时，可能出现计算难以收敛或求解结果不唯一的情况。

图9 最优离散方案下计算精度随离散点变化规律曲线族Fig.9 Variation between losses computational accuracy and discrete points by using optimal discretization method

3.3 考虑实际槽型结构

图8与图9所示为优化离散方案应用在转子矩形导条情况下的计算结果；而针对图3(b)所示实际槽形结构，基于研究所采用的规则性剖分，在不同形状区域(如Ω1、Ω2、Ω3)的交界面处，需必然引入节点，从而3.2节的方法不能直接应用于整个求解域Ω，需要对其进行适当的变换及补充。

首先定义交界面处节点为yΩ1-0，yΩ2-0，yΩ3-0，并针对Ω1、Ω2、Ω3区域，分别采用3.2节所述方法求解一次最优离散解yΩ1-1，yΩ2-1，yΩ3-1，之后以[yΩ1-0，yΩ1-1，yΩ2-0，yΩ3-0]，[yΩ1-0，yΩ2-0，yΩ2-1，yΩ3-0]，[yΩ1-0，yΩ2-0，yΩ3-0，yΩ3-1]作为区间计算3次数值积分解，并与解析解进行误差对比EΩ1-1、EΩ2-1、EΩ3-1，取其最小误差下的值作为“真解”(如yΩ1-1)，相当于在整个求解区域Ω中插入了1个最优离散点。在此基础上，循环采用该方法进行分析计算，并逐次增加离散点及离散区间，最终得到实际槽形的优化离散方案，该方法的几何表示如图10所示。

图11所示为针对实际槽形不同谐波情况，进行8点最优离散的结果，其中数字“①～⑤”表示离散点插入的顺序。由图可见，虽然转子导条电流密度大部分集中于表面位置(即Ω3区域对于损耗应该起主导性作用)，但计算结果却表明：针对本算例，对精度起主要作用的离散点往往在Ω1区域，这是由于Ω1区域电流密度的分布特性较之Ω3区域具有更强的非线性特征，从而使得该区域增加离散点对总体计算精度产生更大的贡献。此外，针对不同的谐波次数，优化离散的策略亦不相同。

图10 实际槽形结构优化离散方法的几何表示Fig.10 Geometric representation of optimal discretization method considering actual structure of rotor bar

图11 实际槽形结构下的优化离散方案Fig.11 Optimal discretization method based on actual structure of rotor bar

图12所示为针对实际槽形结构的电机，在不等间距优化离散方案下，不同次数的转子谐波损耗误差随空间离散密度变化的规律曲线族。

综上所述，对于不等间距的离散方案，不同次数的谐波损耗随离散密度的变化具有很强的一致性，从而该特性可作为判断转子整体谐波损耗的依据。例如，对于图12所示情况，当采用9点离散时，图中所示各次谐波损耗误差均约为5%，从而总体损耗误差亦约为5%。

图12 优化离散方案下计算精度随离散点变化规律曲线族(考虑实际槽形结构)Fig.12 Variation between losses computational accuracy and discrete points by using optimal discretization method (actual structure of rotor bar)

4 结 论

利用时步有限元方法研究同步电动机转子铜耗时，由于所研究的对象包含大量高次谐波分量，为实现精确计算，需考虑离散密度对其计算精度的影响。为此针对转子谐波损耗分析的时步有限元离散策略进行了研究，并得出如下结论：

1)结合理论分析及实际仿真计算结果对比，转子导条沿横向(切向)离散一般采用2～4等分即可满足计算精度要求(参见第2节与表1结论)。

2)针对理想矩形槽结构转子，导条沿纵向(径向)离散可采用等间距与不等间距两种方式，离散密度对损耗计算的影响可由3.1与3.2部分的方法确定。其中不等间距离散通过构造目标函数及求解非线性代数方程组所得到的状态变量解，即为该情况下的最优离散点。

3)针对实际槽形结构转子，由于受到交界面处强制节点条件的约束，可通过3.3节所提出的分段循环插入最优离散点方法进行计算，最终得出全局优化离散方案及其对于损耗计算的影响。

4)该方法可实现不同离散密度下的误差计算预测，并在相同计算精度要求下能够得出最优的离散方案，使得计算量大幅减小。通过表1所示算例可见：离散过于稀疏，将使得损耗的计算精度产生较大的误差，而一味的增加离散密度将导致计算时间大幅增长，而且当其到达一定程度后(Ny>11)，将对计算精度的提高贡献很小(表中Nx、Ny、Nn分别为导条切向、径向、及模型总体的离散点数，Tc为仿真计算总时间、Pcu为转子铜耗)。

表1 不同离散密度下永磁电机转子铜耗与仿真时间的时步有限元计算结果对比

5)该方法同样适用于鼠笼式异步电动机的转子铜耗分析，其中所研究的谐波次数根据具体计算情况确定。

[1] KAZUMI K，GENJIRO W，TOMOTSUGA K.Steady-state performance analysis of permanent magnet synchronous motors including space harmonics[J]．IEEE Transactions on Magnetics，1994，30(3)：1306-1315．

[2] BYUNG T K，BYUNG I K，SEUNG C P．Distribution of the harmonic copper loss in the rotor bar of a traction motor[C].Magnetics Conference,2000．INTERMAG 2000 Digest of Technical Papers．2000 IEEE International 4-8,April 2005:258-258．

[3] LIN D，BATAN T，FUCHS E F et al．Harmonic losses of single-phase induction motors under nonsinusoidal voltages[J]．IEEE Transactions on Energy Conversion，1996，11(2)：273-286．

[4] 吴新振，王祥珩，罗成．异步电机转子感应非正弦电流时的导条损耗[J]．中国电机工程学报，2005，25(17)：132-135． WU Xinzhen，WANG Xiangheng，LUO Cheng．Loss calculation for induction machine rotor bar with non-sinusoidal current[J]．Proceedings of the CSEE，2005，25(17)：132-135．

[5] 汤蕴谬．电机内的电磁场(第二版)[M]．北京：科学出版社，1998: 133-137,212-234,364-367.

[6] 王泽忠，全玉生，卢斌先．工程电磁场[M]．北京：清华大学出版社，2004:180-188.

[7] 陈世坤．电机设计[M]．北京：机械工业出版社，1990:126-129.

[8] HO S L,LI H L,FU W N,et al．A novel approach to circuit-field-torque coupled time stepping finite element modeling of electric machines[J].IEEE Transaction on Magnetic,2000,36(4)：1886-1889．

[9] 黄东洙，李伟力，王耀玉，等．磁性槽楔对永磁电机转子损耗及温度场影响[J．电机与控制学报，2016，20(1)：60-66． HUANG Dongzhu, LI Weili, WANG Yaoyu, et al. Influence of magnetic slot wedge on rotor losses and temperature field of PMSM[J]．Electric Machines and Control, 2016,20(1):60-66.

[10] 曹君慈，李伟力，钱荣超．导磁导电复合笼条转子感应电动机性能计算[J]．电机与控制学报，2015，19(6)，28-34． CAO Junci, LI Weili, QIAN Rongchao. Calculation of performance in induction motor with compound cage rotor of permeability and conductive material[J].Electric Machines and Control, 2015,19(6), 28-34.

[11] 卢伟甫，赵海森，罗应立．自起动永磁同步电动机非正常运行工况下退磁磁场分析[J]．电机与控制学报，2013，17(7)：7-14． LU Weifu，ZHAO Haisen，LUO Yingli. Analysis of demagnetization field of line-start permanent magnet synchronous motor under abnormal operation conditions[J]．Electric Machines and Control, 2013,17(7):7-14.

[12] 李伟力，仝世伟，程鹏．离网型永磁同步发电机电磁场和温度场数值计算与分析[J] ．中国电机工程学报，2010，30(30)：107-113． LI Weili,TONG Shiwei,CHENG Peng.Calculation and analysis of electromagnetic and temperature fields in off-grid type permanent magnet synchronous generator[J]．Proceedings of the CSEE，2010，30(30)：107-113．

[13] 刘秀君，李伟力，陈文彪．三相异步起动永磁同步电动机起动特性[J]．电机与控制学报，2006，10(3)：269-274． LIU Xiujun,LI Weili,CHEN Wenbiao.Analysis of starting characteristics of three-phase line-start permanent magnet synchronous motor[J].Electric Machines and Control,2006,10(3):269-274.

[14] 严登俊，刘瑞芳，胡敏强，等．鼠笼异步电机起动性能的时步有限元计算[J]．电机与控制学报，2003，7(3)：177-181． YAN Dengjun,LIU Ruifang,HU Minqiang,et al.Transient starting performance of squirrel cage induction motor with time-stepping FEM[J].Electric Machines and Control,2003,7(3): 177-181.

[15] 胡敏强，黄学良．电机运行性能数值计算方法及其应用[M]．南京：东南大学出版社，2003：173-179.

[16] 徐士良．数值分析与算法[M]．北京：机械工业出版社，2007:66-67.

[17] 李庆扬，王能超，易大义．数值分析(第4版)[M]．北京：清华大学出版社，2001:85-87.

[18] 梁艳萍，陆永平，朱宽宁，等．汽轮发电机失磁异步运行时转子端部漏磁参数与涡流损耗的分析计算[J]．中国电机工程学报，2004，24(11)：112-115． LIANG Yanping,LU Yongping,ZHU Kuanning,et al．Calculation of leakage reactance and eddy current losses in the rotor end region of large turbogenerator at asynchronous operation[J]．Proceedings of the CSEE，2004，24(11)：112-115．

[19] 罗成，王祥珩，宁圃奇．十二相高速异步发电机转子损耗[J]．清华大学学报(自然科学版)，2006，46(1)：9-12． LUO Cheng，WANG Xiangheng，NING Puqi．Rotor losses in a twelve -phase high-speed asynchronous generator[J]．Journal of Tsinghua University(Science and Technology)，2006，46(1)：9-12．

[20] 宁玉泉，钟长青．大型感应电动机的离散优化设计[J].中国电机工程学报，1997，17(2) ：129-133． NING Yuquan，ZHONG Changqing．Discrete optimal design of large induction motors [J].Proceedings of the CSEE，1997，17(2)：129-133．

[21] 旷建军，阮新波，任小永．集肤和邻近效应对平面磁性元件绕组损耗影响的分析[J].中国电机工程学报，2006，26(5)：170-175． KUANG Jianjun，RUAN Xinbo，REN Xiaoyong．Analysis of skin and proximity effects on winding losses in planar magnetic components [J].Proceedings of the CSEE，2006，26(5)：170-175．

Optimization discrete strategy of time-stepping finite element for loss analysis in rotor bar of line-Start permanent magnet synchronous motor

HU Jia1， GU Jun2， XI Lin-gen1， LÜ Ke-qi1

(1.China Power International Holding Ltd.,Beijing 100080,China;2.Beijing Electric Power Research Institute,Beijing 100075,China)

When calculating copper loss in the rotor bar of permanent synchronous motor (PMSM) using time-stepping finite element method (T-S FEM),there are lots of high frequencies harmonic magnetic fields in the space,the current and loss density distributes non-uniformity because of skin effect,so the method of spatial discretization affects the computational accuracy directly.The current density expression was presented by theoretical deduction firstly,then the object function in different forms was established to research the computational accuracy under the condition of uniform and ununiform discretization,and the optimal discretization strategy was obtained.Finally,considering the constraint condition of the forced node in the interface of rotor bar,the method of optimal discretization calculating loop quoted in different regions was proposed to solve the global optimization problem.The rationality of method was validated by comparing with calculation result of T-S FEM.

time-stepping finite element method; permanent magnet synchronous motors; loss analysis; spatial discretization; harmonic

2015-10-21

胡 笳(1982—)，男，博士，研究方向为电机电磁场数值计算等； 谷 君(1982—)，女，博士，研究方向为电力系统自动化技术及数值计算等； 奚林根(1968—)，男，学士，研究方向为电力系统自动化； 吕克启(1970—)，男，学士，研究方向为电机与电器。

胡 笳

10.15938/j.emc.2017.05.011

TM 351

A

1007-449X(2017)05-0081-08