初中生数学学业自我概念调查研究

邓凡茂,齐永芹

(1.安徽师范大学 数计学院，安徽 芜湖 241000; 2.安徽电子信息职业技术学院，安徽 蚌埠 233030)

初中生数学学业自我概念调查研究

邓凡茂1,齐永芹2

(1.安徽师范大学 数计学院，安徽 芜湖 241000; 2.安徽电子信息职业技术学院，安徽 蚌埠 233030)

采用新修订的初中生数学学业自我概念量表，调查初中生数学学业自我概念，并从性别与成绩排名的角度进行差异性分析，结果表明：(1)初中生数学学业自我概念总值及各个维度的分量均处于中等水平；(2)初中生数学学业自我概念无论是自我认知、自我体验和自我调控的三个维度，还是数学学业自我概念总值均不存在性别显著差异；(3)不同成绩排名分段的初中生，数学学业自我概念中的自我认知、自我体验和自我调控的三个维度及数学学业自我概念总值均存在显著差异。结论：初中生数学学业自我概念存在较大发展空间，对于成绩排名其差异性显著，但性别差异不显著。

初中生；数学学业；学业自我概念；性别；成绩排名

学者们对学业自我概念的定义不尽相同。Byrne(1986)认为自我概念是关于自己的特长、能力、外表和社会接受性方面的态度、情感和知识的自我知觉。[1]House(1992)认为是学生对其学业能力的自我知觉，是学生对自己在学业任务中能否获得成功，能否掌握某一具体的、确定的学业任务的预期和判断。[2]李叶、田学红(2002)认为学业自我概念是学习者对自身学业方面的知觉和评价。[3]姚计海、申继亮(2003)提出学业自我概念是学生把自己当作客体，对自己在学校中的学习能力、态度、体验和价值等做出的整体认识和评价。[4]我们秉持国内知名学者黄希庭、林崇德、杨治良等人的观点(2003)，认为学业自我概念主要包括自我认知、自我体验和自我控制等主要成分。[5]关于学业自我概念与成绩的关系，人们的研究结论也并不一致，如晓惠等(2016)认为：学业自我概念与学业成绩因果关系顺序的诸多研究呈现出不一致的结果，这也足以说明两者之间关系的复杂性，两者之间的相互影响可能并不是直接的，而是存在其它的中介变量。[6]陈京军等(2014)发现：初中生数学学业能力自我概念在数学成绩和数学学业情绪间起完全中介作用。[7]采用初中生数学学科自我概念量表，对初中生数学学业自我概念进行调查，并从性别与成绩排名的角度进行差异性分析。

1 研究设计

1.1 被试

研究的被试为七、八年级学生。在安徽省芜湖和蚌埠两市的三所初中(其中一所为市区中学，一所为县城中学，一所为乡镇中学)在七年级和八年级两个年级采用随机整群抽样(九年级为毕业班未能参与抽样)，每所初中每个年级随机抽取一个班级，共发放问卷354份，全部收回，剔除无效问卷，得到有效问卷315份。结果如表1所示。

表1 被试人口学特征

1.2 研究工具

1.2.1 初中生数学学业自我概念量表

采用裴昌根[8]在对Marsh等人1984年编制的“自我描述问卷(SDQ-Ⅱ)中的数学学业自我概念量表进行修订的基础上，所得到的初中生数学学科自我概念量表，修订后的问卷各子量表内部一致性系数分别为：自我认知0.833、自我体验0.909、自我调控0.681、总量表0.887，量表具有较高的同质性。

1.2.2 SPSS 22.0 运用SPSS22.0软件进行数据的录入、审核及统计分析。

1.2.3 研究过程 由主试采用班级团体施测的形式，测试时间约10分钟。

2 研究结果

2.1 初中生数学学业自我概念的总体情况

从总体来看，初中生数学学业自我概念总值及各个维度的分量均处于中等水平。结果如表2所示。

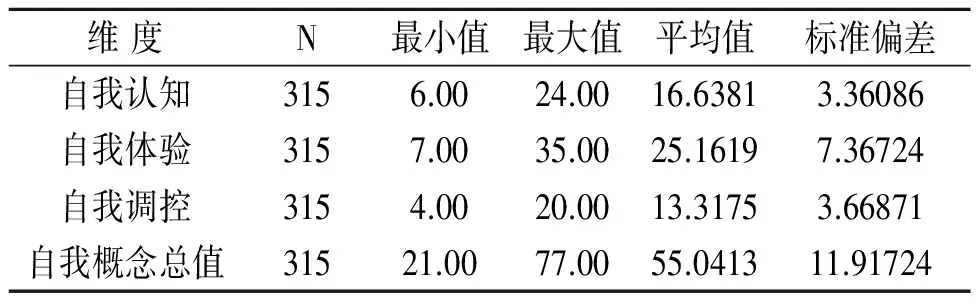
表2 总体情况描述统计

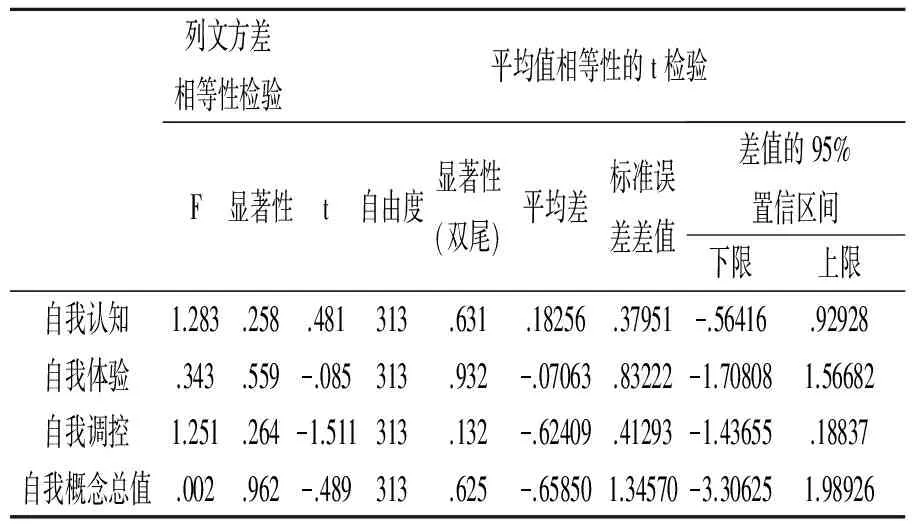
表3 性别差异独立样本检验

2.2 初中生数学学业自我概念的性别差异

经对男女初中生数学学业自我概念进行独立样本t检验，发现：初中生数学学业自我概念无论是自我认知、自我体验和自我调控的三个维度，还是数学学业自我概念总值均不存在显著差异。结果如表3所示。

2.3 初中生数学学业自我概念基于成绩分段排名的差异

经对初中生数学学业自我概念进行学业成绩分段排名的单因素方差分析，发现：初中生数学学业自我概念中的自我认知、自我体验和自我调控的三个维度及数学学业自我概念总值总体检验的F值分别为：59.350(p=0.000<0.05)、19.216(p=0.000<0.05)、24.156(p=0.000<0.05)、43.752(p=0.000<0.05)，均达到显著水平，因此不同成绩排名分段的初中生，其数学学业自我概念中的自我认知、自我体验和自我调控的三个维度及数学学业自我概念总值均存在显著差异。结果如表4-1所示。

表4-1 成绩分段排名差异的ANOVA

由于初中生数学学业自我概念中的自我认知、自我体验和自我调控的方差均符合同质性假设，故对可它们进行Scheffe(C)法的事后多重比较，发现：无论是自我认知、自我体验，还是自我调控，初中生样本中前10名、11～30名、30名以后各个分段的两两之间，均存在显著差异。例如：因变量自我认知对于自变量前10名样本与11～30名的样本分平均差为2.76581*，标准误差为0.39683，显著性为p=0.000<0.05,达到显著水平，说明前10名样本的自我认知平均值显著高于11～30名样本的自我认知平均值，且高出2.76581。而因变量自我认知对于自变量前10名样本与30名以后的样本分平均差为4.86964*，标准误差为0.44830，显著性为p=0.000<0.05,达到显著水平，说明前10名样本的自我认知平均值显著高于30名以后样本的自我认知平均值，且高出4.86964。结果如表4-2示。

表4-2 成绩分段排名差异的多重比较(一) Scheffe(C)

*. 均值差的显著性水平为 0.05。

而初中生数学学业自我概念总值的方差不符合同质性假设，故对可它进行Tamhane法的事后多重比较，发现：数学学业自我概念总值初中生样本中前10名、11～30名、30名以后各个分段的两两之间，均存在显著差异。例如：因变量数学学业自我概念对于自变量前10名样本与11～30名的样本分平均差7.96175*，标准误差为1.50011，显著性为p = 0.000 < 0.05,达到显著水平，说明前10名样本的数学学业自我概念总值平均值显著高于11～30名样本的自我概念总值平均值，且高出7.96175。而因变量数学学业自我概念总值对于自变量前10名样本与30名以后的样本分平均差为15.43929*，标准误差为1.76454，显著性为p = 0.000 < 0.05,达到显著水平，说明前10名样本的数学学业自我概念总值平均值显著高于30名以后样本的自我认知平均值，且高出15.43929。结果如表4-3示。

表4-3 成绩分段排名差异的多重比较(二)

Tamhane 因变量: 自我概念总值

(I)成绩排名(J)成绩排名平均差(I-J)标准错误显著性95%置信区间下限值上限前10名11～30名7．96175∗1．50011．0004．336711．586830名以后15．43929∗1．76454．00011．181819．696711～30名前10名-7．96175∗1．50011．000-11．5868-4．336730名以后7．47753∗1．45437．0003．966310．988730名以后前10名-15．43929∗1．76454．000-19．6967-11．181811～30名-7．47753∗1．45437．000-10．9887-3．9663

*. 均值差的显著性水平为 0.05。

3 讨论分析

总体来看，初中生数学学业自我概念总值及各个维度的分量均处于中等水平，一方面说明，我国初中生数学学业自我概念发展态势良好，另一方面也说明，这还有一定的发展空间，需要在数学教学中逐步提升。与徐富明等(2008)研究结论男生数学学业自我概念显著高于女生不同[9]，我们发现：

初中生数学学业自我概念无论是自我认知、自我体验和自我调控的三个维度，还是数学学业自我概念总值均不存在显著差异，这很可能与老师对学生的数学学习、特别是父母对子女的数学学习的性别无差异关注有关，这尚需要做进一步的研究。分处不同成绩分段的初中生，其数学学业自我概念中的自我认知、自我体验和自我调控的三个维度及数学学业自我概念总值均存在显著差异，且前10名学生既显著高于11-30名学生，更显著高于30名以后的学生，而11-30名学生也同样显著高于30名以后的学生，这说明初中生数学学业自我概念与其数学成绩存在较大的正相关，数学成绩越好，其数学学业自我概念水平也越高，这也符合人们的认知常识。

[1]Byrne B, Self-concept academic achievement relations: stability and causality, Canadian Journal of behavioral science,1986,18: 173 -186.

[2]House J. D. The relationship between academic self-concept, Achievement-related expectancies and college attrition. Journal of College Student Development, 1992, 33:5-10.

[3]李叶,田学红.中学生学业自我概念与学业成就的相关研究[J].湖北民族学院学报(哲社版),2002,20(3):76-79.

[4]姚计海,申继亮,张彩云.中学生偶像崇拜与学业自我概念、学业成绩的关系研究[J].应用心理学，2003,9(1):18-23．

[5]林崇德,杨治良,黄希庭.心理学大辞典[M].上海:上海教育出版社,2003:1492.

[6]陈晓惠,石文典. 中小学生学业自我概念与学业成绩的交叉滞后分析: 符合交互影响模型，还是发展观? [J].心理发展与教育, 2016,32(1):81-88.

[7]陈京军,吴鹏,刘华山.初中生数学成绩、数学学业能力自我概念与数学学业情绪的关系[J].心理科学, 2014,37(2): 368-372.

[8]裴昌根.初中生数学学科自我概念量表的编制及其应用[D].西南大学硕士学位论文,2009:17.

[9]徐富明,施建农,刘化明. 中学生的学业自我概念及其与学业成绩的关系[J].中国临床心理学杂志, 2008,16(1):59-62.

Investigation and Analysis of Mathematics Academic Self-concept of Middle School Students

DENG Fan-mao1, QI Yong-qin2

(1.School of Mathematics and Computer Science, Anhui Normal University, Wuhu Anhui 241000, China; 2. Anhui Vocational College of Electronics and Information Technology, Bengbu Anhui 233030, China)

By using the newly revised middle school students mathematics academic self-concept scale, this paper investigates the self-concept of middle school students and analyzes the differences from the perspective of gender and performance ranking, and the results show that: (1)Gross mathematics academic self-concept of middle school students and the components of each dimension are in the medium level;(2)There are no distinct gender difference in both three dimensions of middle school students’ mathematics academic self-concept, namely self-cognition, self-experience and self-regulation, or in the gross of mathematics academic self-concept;(3)Middle school students with different ranking section have significant differences in the gross of mathematics academic self-concept and in the three dimensions of self-cognition, self-experience and self-regulation as well as in mathematical academic self-concept. Conclusion: there is a great development space for middle school students’ self-concept in mathematics academic. And while the difference of students with different ranking section is significant, the gender difference is not significant.

junior middle school students; mathematics study; academic self-concept; gender; performance ranking

2017-01-06

国家社科基金项目(11BKS067);安徽省高校人文社科研究重点项目(SK2015A586);安徽省质量工程教学研究项目(2013jyxm428);安徽省教育科学规划项目(JG13004);安徽省弘扬核心价值观名师工作室(Szzgjh1-1-2017-30);安徽省高校人文社科研究重点项目(SK2015A588);安徽省教育科学规划重点课题(JG11020)。

邓凡茂(1976-)，男，安徽蚌埠人，讲师，硕士，研究方向为数学教育心理。

G62

A

1674-344X(2017)2-0129-04