无传感器永磁同步电机模型参考模糊自适应系统

赵换丽,王 艳,许允之

(1.平顶山学院,河南467000;2.中国矿业大学,徐州221116)

0 引 言

永磁同步电机因高效、高功率密度、高转矩密度及高可靠性而被广泛使用。但使用传感器的电机增加了系统的复杂性并降低了整体系统的可靠性,因此永磁同步电机的无传感器控制方法受到普遍关注并进行了广泛研究。

模型参考自适应算法是一种易于数字化的电机转速和位置观测算法,在各类参数辨识中均获得了良好的应用[1-2]。然而此系统的缺点在于依赖于观测器的准确度,尤其是当电压模型受到定子电阻值影响而产生变化时。采用定子电阻观测器可以补偿以上弊端,但是同时进行多参数辨识明显降低了系统的响应速度[3]。

为了从本质上解决模型参考自适应系统对参数的敏感性问题,诸多文献提出将不依赖参数的模糊逻辑或滑模算法融入其中[4-6]。为了提高含有滑模控制的MRAS系统的精度和稳定性,设计二阶滑模结构的复杂度较高[4]。相比之下模糊系统结构较为简单,且执行效率更高。文献[5]将系统多个状态输入单一的模糊控制器,共设计了7个逻辑子集,模糊蕴涵关系过于复杂,隶属度函数校验成功率较低。

鉴于系统缺陷和已有的研究经验,本文将模型参考自适应结构中传统的PI调节器替换为非线性模糊逻辑单元,提出基于模型参考自适应的两级式模糊逻辑系统结构。两级式结构有效地降低了参数间的耦合性,同时提高了转速跟踪性能,并在不同的工况下提供优异的自适应能力将转速误差降到最小。

1 模型参考自适应系统机理分析

使用模型参考自适应算法的目的是为了更加精确的观测定子d,q轴的电流和电机转速。模型参考自适应系统从结构上包括参考模型和可调模型。参考模型的作用是用以确定已知的定量值,可调模型作为一个自适应模型可根据不同给定值产生相应的期望输出结果。再将参考模型的输出和可调模型进行比较,并将两者输出误差信号送入自适应机中,获得估算的电机转速反馈至可调模型中。常规的模型参考自适应算法估算转速的结构框图如图1所示。

图1 模型参考自适应系统结构框图

设d-q坐标系为永磁同步电机中的同步旋转坐标系,则电机在此旋转坐标系下的数学模型:

式中:vd和vq分别表示d轴和q轴的定子电压分量;Ls和Rs为定子电感值和电阻值;ωr为转速;ψr为转子磁链。将以上电流方程写为矩阵形式:

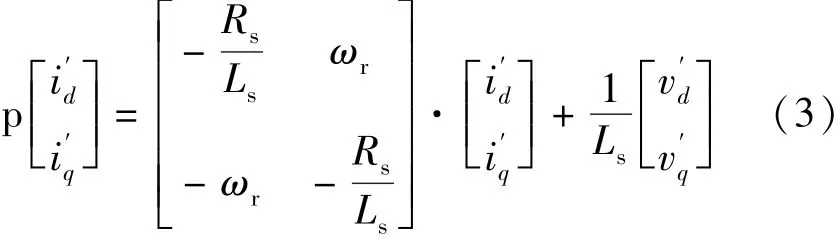
式中:

式(3)中存在时变量ωr,因此作为可调模型。永磁同步电机作为参考模型,并产生id和iq两个参考值。则根据以上关系可设计出基于常规PI的模型参考自适应控制系统。对式(3)进一步简写可得:

因此可调模型的数学方程如下:

同理,式(6)可以简写:

在此模型中,ωr是需要观测的量,其它参数均为定值。则电流误差:

结合波波夫稳定性系统判据,则串联模型的数学表达式:

式中:

依据波波夫超稳定性理论,如果系统满足:

1)状态矩阵H(s)=D(sI-A)-1严格为正实数;2)波波夫积分不等式

对于∀t0≥0,是一个与t0相关的有限正常数。

满足以上条件,则设计的模糊模型参考自适应系统满足渐进稳定性。若系统继续满足tl→im∞e(t)=0,则基于此MARS的系统是绝对稳定系统。

因此,结合以上分析可推导出估算算法的数学模型如下:

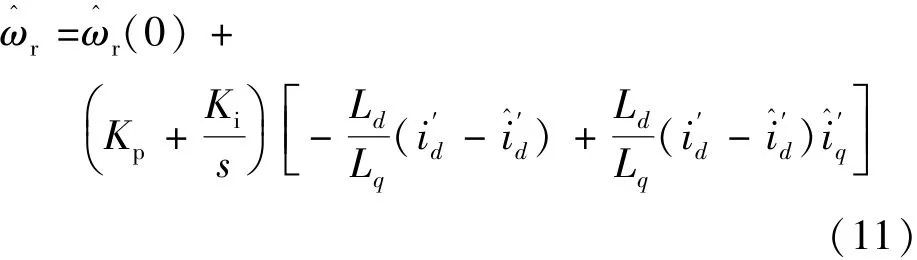
将式(4)代入式(11)时可得:

动漫旅游的核心竞争力是动漫游艺作品带给观众的体验和心灵的感受，动漫在旅游中能够让人们找到与动漫人物的共鸣，进行深度的体验，因此动漫IP在整个动漫旅游中为最重要的一环，如何打造一个成功的动漫IP，才是第一步要做的。打造动漫IP有几种形式：

式中:通过可调模型计算获得;id,iq通过参考模型获得。所采用的为混合自适应律方法,此算法在高度非线性系统建模分析中具有明显优势,应用到模型参考自适应亦可获得良好性能。

2 模型参考模糊自适应系统设计

传统模型参考自适应系统的结构系统如图1所示,系统中的永磁磁链和电感值受系统运行状态和实际参数影响较大。为了减弱甚至消除原系统中对于永磁磁链和电感的依赖性,引入模糊控制系统结构并演化出图2的结构框图,因此,含模糊系统的新结构系统响应大幅提高,稳态误差大幅降低。

图2 两种系统自适应结构框图对比

模糊系统对实际系统和控制对象的数学模型无依赖性,对系统状态的自适应性能更好,尤其在非线性系统中应用广泛[7-8]。

使用模糊控制的本质是为了减少迭代计算的次数以降低处理器的计算耗时。在常规的模糊逻辑系统中,所涉及的规则总数急剧增长,当采用多级串联结构时,可调节控制规则增长方式为线性。

所提结构包括两个模糊系统单元,对系统参数进行相关度分析,将相关度高的系统变量从第一层结构中输入,相关度低的变量从第二层结构中输入。实际上,在此结构中每个双输入模糊逻辑控制器均引入了辅助增益系数以辅助调节系统性能,采用双输入结构相比常规的单输入模糊控制器规则更加精简,同时此结构下的模糊规则数量也可以因此而减少[5]。

本算法将3个变量(e1+Δe1+Δe2)作为输入进行计算。模糊系统的元素规则表如表1所示。分别有正(P)、负(N)、零(Z)3种状态。本文中,所提出的结构采用两级模糊子系统,每个子系统仅含有两个输入信号。第一个子系统的输入信号为e1和Δe1,输出为Δu1,并结合Δe2作为第二级子系统的输入,如图3所示。

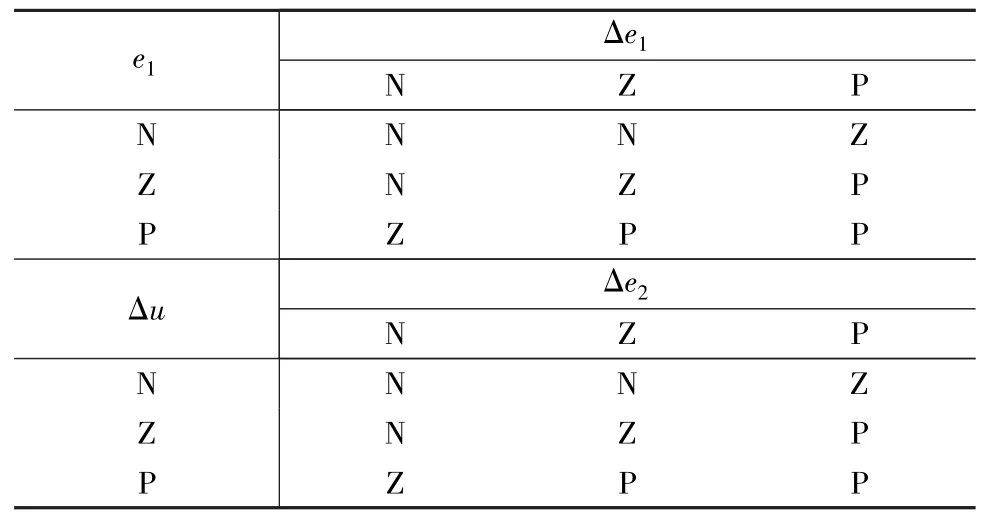
表1 子系统的模糊逻辑规则表

图3 两级模糊系统结构示意图

模糊系统中的误差变量e1和e2的定义如式(13)、式(14)所示,Δe1和 Δe2分别为其对应的增量。在本模糊系统中,第一个输入信号为e1;第二个输入信号为Δe1,此信号与e1的变化速度相关;第三个输入信号为Δe2,此值由e2的增量信号获得。

图3中的k1～k5为输入输出信号的辅助增益系数,具体取值可根据相应的应用场景进行调整以改善系统的性能。本文中各项增益的具体取值为k1=k2=k3=k4=1,k5=0.1。

采用三角形隶属函数定义如图3所示的两组模糊系统。本研究采用Mamdani模糊逻辑推理类型和质心解模糊化方法辅助调整模糊子系统的隶属度函数。

因本系统采用双层串联型模糊控制单元,第一层单元中的参数对系统状态的影响权重较高,因此其隶属度函数设计较为严苛。结合表1的控制规则,第一层模糊子系统的录属度函数如图4所示。

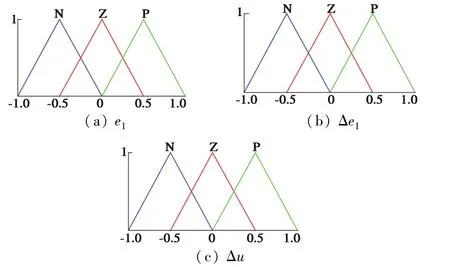
图4 第一层模糊子系统的录属度函数

3 实验分析

在实验分析中,DC直流电压输入为311 V,逆变器采用SVPWM控制方式,开关频率为10 kHz,通过电流及电压传感器将信号采集并AD转换后输入DSP芯片进行计算处理。实验所采用的控制拓扑结构如图5所示,电机主要参数如表2所示。

图5 采用MARS的永磁同步电机矢量控制系统结构框图

表2 实验电机的额定参数

3.1 动态性能对比

为了对比分析模型参考模糊自适应控制算法与采用PI调节的传统模糊控制算法的具体动态性能,设计实验分析研究了电机低速和高速域的运行情况,具体如下:

工况1:电机初始状态静止,在0.2 s时将给定转速由0突变到100 r/min,并在1 s时将给定转速由100 r/min突变为反向100 r/min。

工况2:电机初始状态静止,在0.2 s时将给定转速由0突变到1 000 r/min,并在1 s时将给定转速由1 000 r/min突变为反向1 000 r/min。

在工况1和工况2下采用两种不同算法的转速实验波形分别如图6和图7所示。由图6、图7可知,模型参考自适应控制性能较弱的低速区域下,引入模糊结构单元后电机在动态响应速度有明显的提升,耗时仅为传统算法的30%左右。高速区域下常规算法性能良好,但是模糊算法对转速的跟踪速度依然更快,约节约时间40%。此外,不同于PI完全依赖于误差输入的调节方式,模糊控制算法在稳态状态下纹波相对较低,调整时间较短,转速误差几乎为0。

图6 低速工况下两种控制算法的转速实验波形

图7 高速工况下两种控制算法的转速实验波形

模型参考自适应算法在电机高速运行时的转子位置检测效果良好,而低速时一般精度较低。在工况1下运行时两种算法的角度估算结果如图8所示。由图8可知,模糊模型参考自适应算法下电机的定位精度更高且定位速度更快,它在低速下的定位精度提高约57%。

图8 低速工况下两种控制算法的位置估算结果

3.2 稳态性能对比

为了分析电机稳态运行全指标的详细性能,实验分析了低速、中速和高速下两种算法的不同指标结果,具体对比如图9所示。图9中纵坐标为相同工况下两种算法的实验结果值总和,横坐标为不同转速工况以及所对应的性能指标。

图9分别实验分析了100r/min,500r/min和1 000 r/min转速情况下两种算法的实际性能。

图9 两种方法不同转速下各项稳态性能指标对比

图9 中含网格底纹的柱形图表示模糊算法下的实验结果,其下方为传统算法的实验结果。由图9可知,在不同转速下,新算法的起动时间、稳态调整时间、转子定位时间、超调量均明显小于传统算法,且优化效果有绝对优势。而低速时的转速误差也有明显降低,在高速域转速误差与传统算法相当。

4 结 语

本文研究并提出了一种针对永磁同步电机的模型参考模糊自适应无传感器控制系统,并将所提出的方法与传统的PI调节器进行对比分析。实验结果表明,采用两级式模糊系统可以有效降低系统的复杂度,从而提升系统的动稳态性能。与传统算法相比,模糊算法弥补了低速域下转速脉动大、转速跟踪慢等缺点,在全速域下平均电机性能提升50%以上。而相比于PI系统,所提方法复杂度无明显提升,适合数字控制系统的推广应用。