超磁致伸缩材料叠堆结构动态涡流损耗模型及性能分析

高嘉纬,黄文美,王 超,古海江,李庆竖

(河北工业大学,天津300130)

0 引 言

超磁致伸缩器件在交变磁场的作用下,发生反复伸张与缩短,从而产生振动或声波,实现不同能量间的转换[1-2]。然而超磁致伸缩材料(以下简称GMM)置于交变磁场中工作会产生感应电动势从而形成较大的涡流效应,致使材料温度过高、效率降低[3]。为了减小涡流损耗,目前绝大多数的GMM采用叠堆结构,将超磁致伸缩棒沿纵向切片,并通过环氧树脂等绝缘材料粘接,从而使涡流损耗大大降低[4]。目前已有的文献对叠堆结构的GMM损耗模型的建立和损耗特性研究较少。

文献[5]分析了GMM的损耗机制,并深入研究了其涡流损耗以及频率相关性。文献[6]利用磁能理论对材料内部涡流损耗进行了分析,用Bessel函数描述GMM内部的磁场分布。文献[7]针对GMM的压磁效应,基于能量最小值理论,分析了磁化过程中磁弹力对材料内部磁场的影响,分析了不同频率下整体材料的涡流损耗和磁滞损耗的频率特性,但未针对叠堆结构的GMM的能量损耗进行分析。文献[8]建立了在考虑涡流损耗因素下的GMM棒内部的磁场分布,以及对GMM棒的涡流损耗效应进行分析,但没有具体分析叠堆结构应用中频率以及切片数对涡流损耗的影响。

本文基于麦克斯韦方程,通过求解GMM叠堆结构在轴向激励磁场下的内部磁场分布,建立了叠堆结构GMM动态涡流损耗模型。与仿真结果对比,验证了模型的准确性,并对其误差进行分析与修正,计算了GMM叠堆结构应用中的涡流的频率特性及其切片数对损耗的影响。

1 GMM叠堆结构动态涡流损耗

影响GMM棒涡流损耗的主要因素包括工作频率f,集肤深度Δ以及涡流截止频率fc[9],其表达式如下:

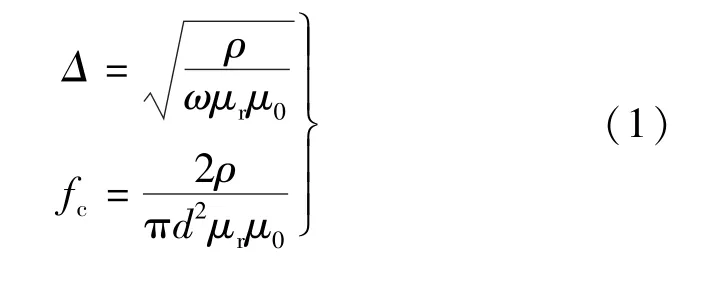
式中:ω=2πf为角频率;μr为相对磁导率;μ0为真空磁导率;ρ为材料电阻率;d为GMM棒直径。

由于GMM的导磁导电性能,GMM在正常工作时,其尺寸一般都要比截止频率所允许的要大一些,这就导致了GMM产生的涡流更加严重,这将导致其工作效率的低下,造成了很多的能量浪费。根据截止频率的公式,相同工作频率下,集肤深度Δ为一定,涡流截止频率越低,材料损耗越明显。因此,通过减小GMM棒的厚度,采用沿纵向方向切片的GMM叠堆结构是减小涡流损耗的有效措施,本文介绍由麦克斯韦推导的GMM叠堆结构的涡流损耗模型。

1.1 GMM切片在激励磁场作用下磁场分布

对于某一切片,外磁场H=H0ejωt沿y轴方向平行于切片表面,x轴垂直于切片表面,则根据麦克斯韦方程组[10]:

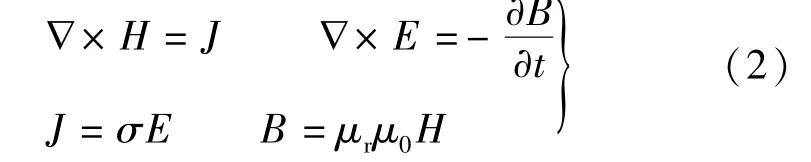
式中:H为磁场强度;B磁通密度;J电流密度;E电场强度;σ为电导率,联立可得:

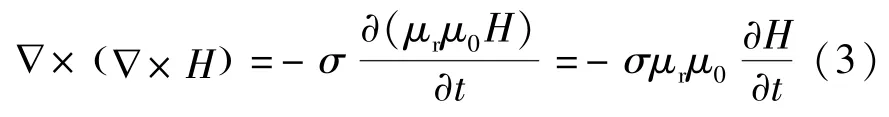
可得外磁场H=H0ejωt条件下,切片结构 GMM棒内部磁场H分布满足微分方程:

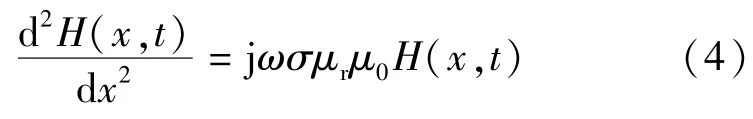
式(4)的二阶常系数微分方程解满足:

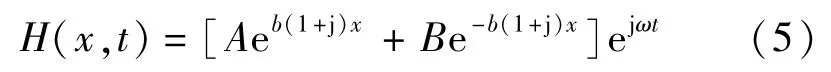
式中:A,B为积分常数,大小由边界条件式(6)决定:

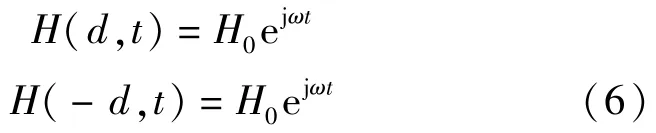
求解二元一次方程组:

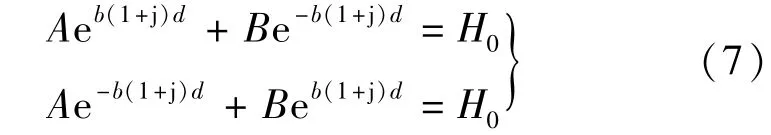
可得积分常数:

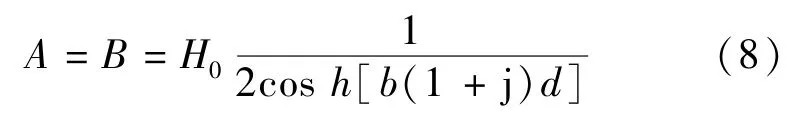
代入积分系数A、B,GMM材料棒中磁场强度分布:

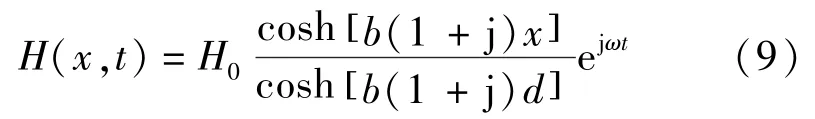
式中:b=(2σωμrμ0)1/2;d为切片厚度的一半;cosh[·]为双曲余弦函数;x为[-d,d]范围内任意参量。

1.2 GMM切片动态涡流损耗模型

动态磁场作用下,GMM棒内产生涡流效应是不可避免的。尤其在高频条件下,涡流损耗较大且直接产生在GMM上,是造成系统大量焦耳热的主要因素。本节将对切片结构GMM材料棒的涡流损耗进行建模计算。

为了减小涡流损耗,叠堆结构磁致伸缩棒沿轴线方向切分成多片,并通过绝缘环氧树脂粘合在一起,其涡流损耗分析原理图如图1所示。

图1 GMM叠堆结构涡流损耗模型分析原理图

如图1所示,磁致伸缩材料棒的直径为2R,沿轴线方向平均切分N片,切片厚度2d满足关系式2d=2R/N。图中满足关系式x=ky,任意切片内部磁场分布满足式(9):

为了求解的方便,将模型中每个叠片的横截面近似为长方形结构,对其中某一叠片的涡流损耗进行计算,首先取切片厚度方向y处、厚度为dy的微方环为研究对象,可得微元体电阻:

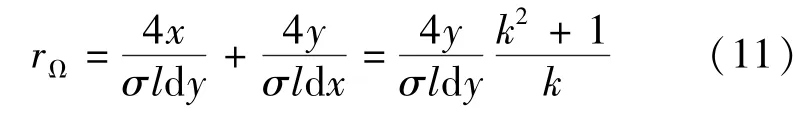
外加激励磁场作用下,由式(10)可知,微元环区域内的平均磁感应强度:

令

在微元体[y,y+dy]区域上感应电动势:则微元体回路上的涡流损耗:

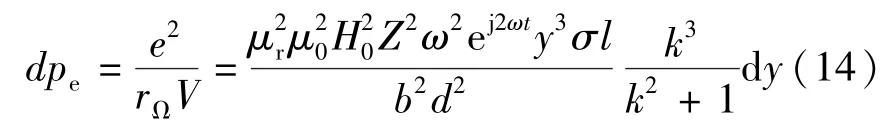
对式(14)在厚度方向积分以及时间积分,得某一切片上的涡流损耗:

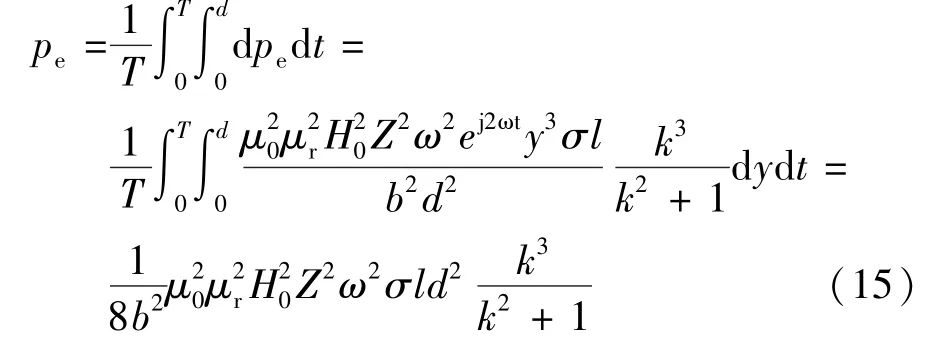
假设GMM棒沿纵向切片数N(N≥2),由几何关系得:

当切片数N为偶数时:

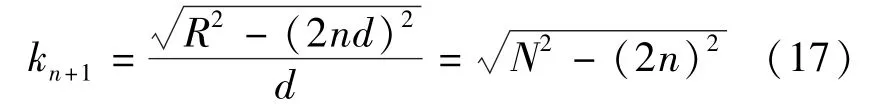
则GMM棒上总涡流损耗:

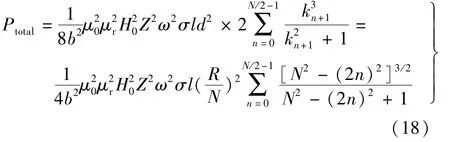
当切片数N为奇数时:

此时GMM棒上总涡流损耗:

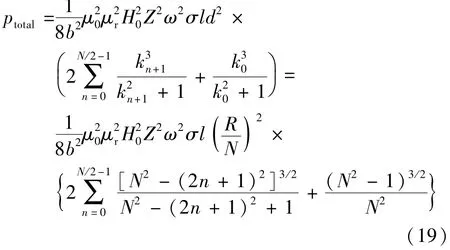
由式(19)可以得出,GMM棒的磁导率、电导率、半径、切片数、频率都是影响涡流损耗的重要参数。

2 GMM叠堆结构涡流损耗仿真分析

在上述GMM涡流损耗模型中,忽略了GMM存在的漏磁,而且假定磁场沿轴向均匀分布,且材料的磁导率较小,磁路中有气隙。因此,需要对GMM切片结构涡流损耗进行有限元仿真分析,来求解更加精确的涡流损耗值。

2.1 GMM叠堆结构的有限元仿真分析

本小节用电磁场分析软件ANSYS MAXWELL建立有限元仿真模型,选取直径10 mm×40 mm的Terfenol-D棒,密度为8.96×103kg/m3,电阻率为6×10-7Ω·m,驱动线圈为400匝,叠堆结构由厚度为2 mm的5片Terfenol-D薄片组成,驱动电流为5 A的正弦信号,对圆柱叠堆GMM结构进行二维涡流场有限元仿真分析。

首先对换能器建立二维几何模型,添加本文所选用的材料属性,并进行网格剖析,如图2所示。

图2 换能器仿真模型与网格剖分图

对上述模型进行求解计算,设定驱动线圈为幅值为5 A的正弦交变电流,驱动频率为500 Hz,得到换能器核心材料叠片结构GMM棒的涡流损耗分布图如图3所示。

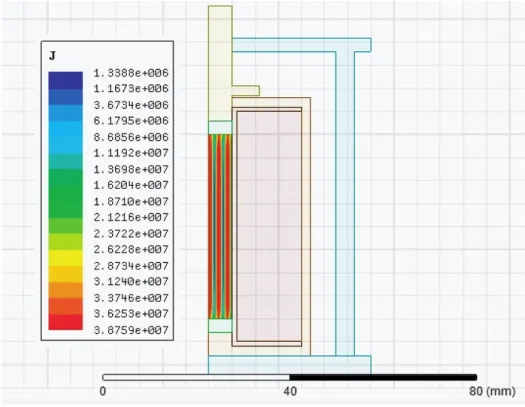
图3 叠片结构GMM涡流损耗分布图

在相同条件参数的情况下,通过对叠堆结构的GMM棒仿真分析,得出涡流损耗大小随频率的关系曲线,与本文之前所建模型计算结果对比分析,如图4所示。

由图4可知,随着驱动激励频率的增大,两条曲线的涡流损耗都逐渐增大,而且呈现出二次函数变化的趋势,模型计算数据与仿真结果基本吻合。由于在模型计算中假定了磁场沿轴向均匀分布,以及GMM的磁导率较小,模型推导过程中对于任意切片采用微元环分析,故使得动态模型推导下的涡流损耗值略大于仿真的涡流损耗数值。

2.2 GMM叠堆结构模型误差分析

(1)对GMM的整体与叠堆结构的磁通密度分布对比。

由图5可见,圆柱块GMM的内部磁场具有明显的趋肤效应,但是其在中心位置几乎没有磁场,将圆柱块GMM切为5片粘接后的叠堆结构的磁场分布则比正常的要好些,而经过切片处理的棒材磁场更加均匀分布了。由此可看出,叠堆结构可以更好地应用在实践中,提高GMM的工作效率。

图5 GMM纵向截面磁通密度分布图

(2)GMM计算模型结果与仿真结果对比与分析

由表1可以得出,对比叠堆结构GMM的磁感应强度和涡流损耗值,可知二者的计算结果都大于仿真结果,并存在一定的误差。主要是由于GMM的磁导率比较小,且实际中与仿真中都存在漏磁。分析误差结果可以得出,叠堆结构GMM涡流损耗计算与仿真结果的比值是GMM磁感应强度计算与仿真结果的比值的平方,这说明了叠堆结构GMM的模型误差主要来源于对磁感应强度的计算,式(12)计算所得的磁感应强度并未考虑漏磁。对本文上述得出的GMM叠堆结构涡流损耗模型中的磁感应强度计算式引入漏磁系数α,可得到更加精确的模型。漏磁系数α可以通过经验估计获得,修正后的磁感应强度计算公式:

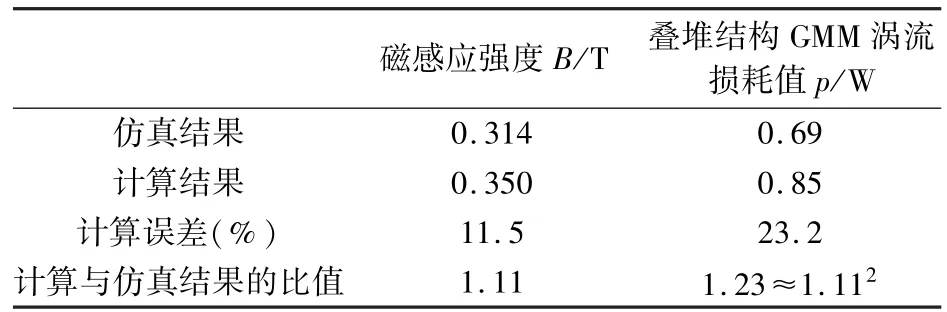
表1 涡流损耗计算结果与仿真结果比较

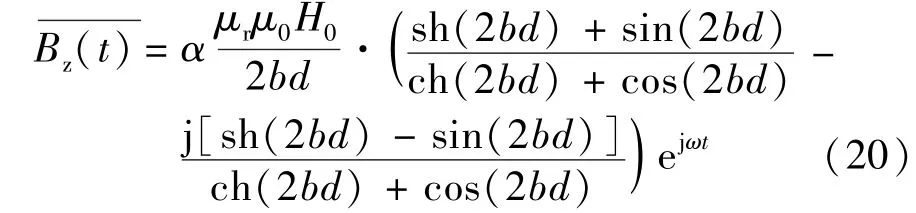
(3)叠堆结构参数影响

由图6可知,GMM叠堆结构处理对于降低材料涡流损耗效果明显。材料棒尺寸一定时,切片数越多,涡流损耗越小,实际工作性能越好。不同励磁频率驱动下,GMM叠堆结构性能改善程度不同,在高频工作环境下,涡流损耗是GMM实际工作损耗的主要因素。由图6可知,驱动频率越大,涡流损耗随切片数的增加下降趋势越明显,当驱动频率为500 Hz时,GMM切片数由2增加到5时,涡流损耗由108.20 W减小到18.3 W,GMM的涡流损耗降低了83%。当GMM切片数由2增加到10时,涡流损耗由108.20 W减小到3.92 W,GMM的涡流损耗降低了96%。受加工工艺水平所限,本文的GMM采用切片数为5的叠堆结构。

图6 影响叠堆结构涡流损耗的主要因素

3 结 语

(1)GMM在磁场作用下将产生较为显著的涡流效应,材料的工作频率、集肤深度以及涡流截止频率直接影响涡流损耗的大小。在相同工作频率下,通过减小GMM厚度来提高其涡流截止频率,是降低涡流损耗的有效方法。

(2)基于麦克斯韦方程组求得叠堆结构切片的磁场分布函数表达式,建立了GMM棒叠堆结构的动态涡流损耗模型。分析可见,叠堆结构可以大幅度降低涡流损耗,动态涡流损耗模型计算结果与仿真结果较为一致。

(3)通过分析计算模型的误差,对计算模型进行了修正,引入漏磁系数α可获得更加精确的GMM叠堆结构涡流损耗模型。同时,在叠堆结构中,随着切片数增多,涡流响应影响越小,对于本文的GMM在5片以内尤为明显,应用中可以采用5片的叠堆结构,在高频工作环境下可有效抑制涡流效应对实际工作的影响。

参考文献

[1] MENG Y N,FU L.Application and development research on giant magnetostrictive apparatus[C]//IEEE Conference Publications,2010,442-445.

[2] WANG B W,BUSBRIDGE S C,LI Y X,et al.Magnetostriction and magnetization process of Tb0.27Dy0.73Fe2single crystal[J].Journal of Magnetism and Magnetic Materials,2000,218(2-3):198-202.

[3] 曾海泉,增庚鑫,曾建斌,等.超磁致伸缩功率超声换能器热分析[J].中国电机工程学报,2011,31(6):116-120.

[4] 贾傲,张天丽,孟皓,等.粘结巨磁致伸缩颗粒复合材料的磁致伸缩性能及涡流损耗[J].金属学报,2009,45(12):1473-1478.

[5] MENG H,ZHANG T,JIANG C.Frequency dependence of loss behavior in bonded anisotropic giant magnetostrictive materials[J].IEEE Transactions on Magnetics,2014,50(9):1-4.

[6] 孙华刚,袁惠群.超磁致伸缩材料内部磁场与涡流损耗理论分析[J].东北大学学报,2008,29(3):371-374.

[7] 李立毅,严柏平,张成明.驱动频率对超磁致伸缩致动器的损耗和温升特性的影响[J].中国电机工程学报,2011,31(18):124-129.

[8] 陶孟仑,陈定方,卢全国,等.超磁致伸缩材料动态涡流损耗模型及试验分析[J].机械工程学报,2012,48(13):146-151.

[9] ENGDAHL G.Handbook of giant magnetostrictive materials[M].San Diego:Academic Press,2000.

[10] MEEKS S W.The equivalent circuit in the mobility analogy of a magnetostrictive transducer in the presence of eddy currents[J].Joural of the Acoustical Society of America,1980,67(2):683-692.