基于直接磁链矢量的感应电机转矩效率最优控制

郭洪英

(国网福建省送变电工程有限公司,福州350013)

0 引 言

随着以电动汽车为代表的绿色电力技术概念的发展,对电力传动的效率也要求越来越高,电机的节能驱动控制技术逐渐成为了一个研究热点[1-3]。相对于感应电机(以下简称IM),永磁电机传动效率和转矩密度更高,因此得到较快发展,但是由于IM具有坚固耐用,工艺简单,成本低、免维护和可以弱磁运行等优点,使得其依然是电力传动的主要电机选型[4-6]。因此,开展IM的驱动效率优化控制,尤其是IM在额定转速以下并处于轻载工况时的效率提升是很有必要的。

文献[7]指出,IM在不同负载下调整合适的磁链可以达到提高效率的目的,具体可以分为3类途径实现。第一种是通过控制一个单一变量,如功率因数[8]或滑差频率[9],两者都是适合于标量控制和间接转子磁场定向矢量控制的,但基于滑差频率的节能控制策略对电机参数依赖较强,鲁棒性一般,而基于功率因数的节能控制策略更适合于低动态驱动应用场合,存在一定局限性。文献[10]给出了IM的最大转矩电流比算法(以下简称MTPA),其通过选择能实现最大转矩的电流来提高IM运行效率,也属于第一种实现途径。第二种途径是基于查询或迭代搜索机制的控制策略,文献[11]针对电动汽车IM驱动提出了一种基于查询图模式的节能驱动控制,输入需要的转矩转速,查询图后生成最佳参考电流,而图是通过一系列包括测量定子温度在内的运算和校准得到的,计算量较大,工程实现难。文献[12]基于测量得到的功率和设定的功率需求进行迭代调整计算和搜索实现效率最优,虽然不依赖于电机参数,但收敛速度较慢,不适合需要较快动态调节的场合。第三种途径是基于电机的损耗模型进行驱动设计,虽然可以直接应用于IM矢量控制,但是依赖的电机参数也较多,例如文献[13]在应用于泵的IM应用上设计了一种考虑了杂散损耗和脉宽调制(以下简称PWM)效应的等效铁损电阻模型,然后使用人工神经网络控制器产生的最佳磁链进行驱动控制,其用到的电机参数较多且计算量大。

本文基于前述研究,设计了一种新型的基于直接磁链矢量的感应电机转矩效率最优(以下简称MEPT)驱动控制方案。新型控制策略是前述3种方案的组合,控制的单一变量是定子磁链,但是最优定子磁链的生成是基于设计好的电机损耗模型,同时模型中含有查询表。MEPT方案可以结合直接转矩控制[14]和直接磁链矢量控制[15](以下简称DFVC)实现。MEPT算法中最优定子磁链参考查询表是通过空载和堵转试验结果,并进行相关离线计算得到的。为了验证新型控制技术的有效性,基于额定功率为2.2 kW的试验电机进行与传统固定磁链算法以及 MTPA算法的对比试验,试验结果证明了MEPT算法效果优于传统算法,具有明显提高IM效率的效果。

1 基于损耗的IM模型

1.1 IM数学模型

通常描述IM动态模型的参考坐标系有α-β静止坐标系、转子dm-qm旋转坐标系、转子磁链d-q旋转坐标系和定子磁链ds-qs旋转坐标系,具体如图1所示。下面将电压、磁链和电流分别用v,λ和i表示,下标“s”和“r”则分别代表定子和转子,λ,λr为矢量。

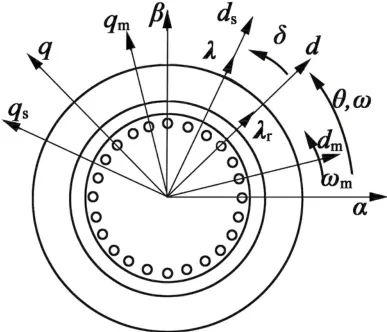
图1 IM模型的参考坐标系定义

图2为转子磁链d-q旋转坐标系下的IM稳态模型。该模型将用来计算效率优化控制设计,图中的相关变量采用矢量描述。

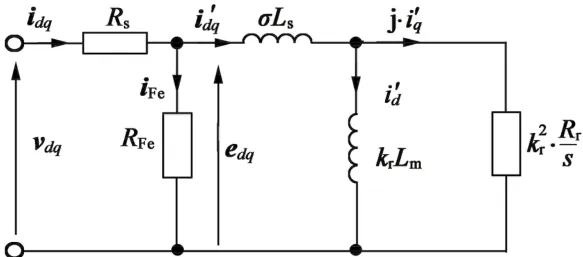
图2 IM稳态等效电路模型

图2中,s代表了滑差系数;σ是漏感系数;Ls是定子电感;Lm是激磁电感;Lr是转子电感;kr=Lm/Lr,kr是转子耦合系数。Rs,Rr和Rfe分别是定子电阻、转子电阻和铁损等效电阻。edq和ife分别为反电动势和铁损等效电流矢量。vdq为d-q坐标系下电压矢量,idq和 i′dq分别为d-q坐标系下电流矢量和去掉铁损后的等效d-q坐标系下电流矢量。为了简化分析过程,图中忽略了机械损耗和一些额外损耗。根据图2的等效电路,可以建立电流磁链方程如下:

式中:Lls和Llr分别为定子和转子的漏电感;λm和im分别为激磁磁链矢量和激磁电流矢量。磁路饱和将通过励磁电感随激磁电流变化的曲线进行描述,而定转子的漏电感默认保持恒定。假设电机处于稳态运行,则定子磁链和电流矢量之间的关系式,以及电压方程如下:

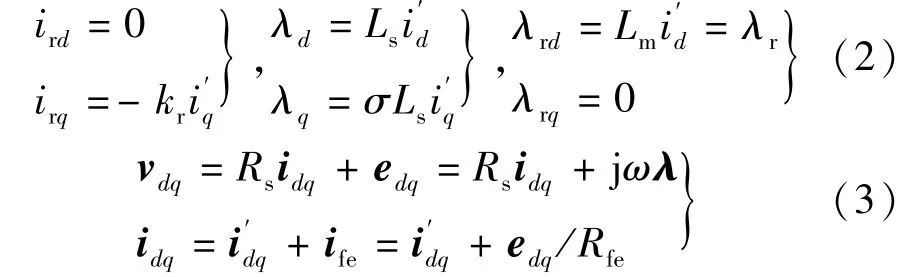
电磁转矩T,同步转速ω和滑差转速ωslip的表达式分别如下[16]:

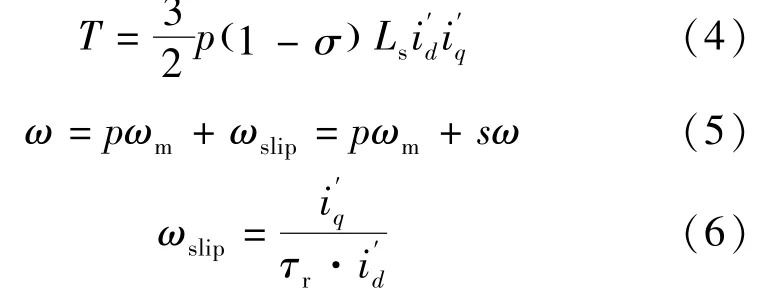
式中:ωm为机械转速;p为极对数,τr=Lr/Rr,τr是转子时间常数。图3为IM在稳态运行时的矢量图。根据式(2)和式(4),定子电流决定了电机磁链和电磁转矩,而总的定子电流还包含了铁损等效电流。而激磁电流矢量幅值近似等于除去铁损后的d轴定子电流,具体如下:

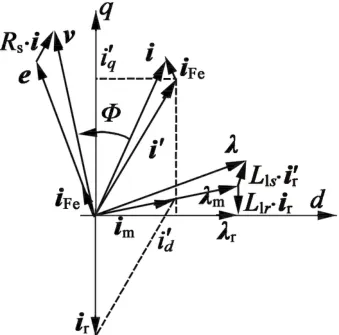
图3 d-q坐标系下的稳态矢量图

1.2 损耗推导

在图2的等效电路中,忽略了机械损耗和一些额外损耗,故电机的损耗主要体现为定转子电阻,以及铁损等效电阻上的损耗,具体可计算如下:

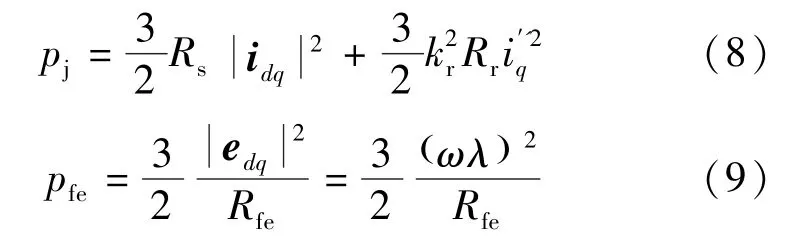
式中:pj为铜耗功率;pfe为铁损功率;ploss为总损耗功率。根据图3的稳态矢量图,可推导得到电机的稳态效率η表达式:

式中:Pm=T·ωm为机械输出功率。在考虑效率优化控制策略时还需要考虑电机温度和转速,以及铁损等效电阻Rfe随磁链的变化。

2 铁损的建模和参数计算

造成电机铁损的主要因素是磁滞损耗和涡流损耗,其中磁滞损耗pHy的计算式[17]:

式中:V是总的铁心体积;f为工作频率;Bmax为磁通密度峰值;n和χ是和磁性材料相关的常数。从式(12)可以明显看出,在计算磁滞损耗时需要电机设计数据和磁性材料数据,因此引入一个常数kHy如下:

式中:A为磁路的面积;N为绕组匝数。因此与几何尺寸相关的量都纳入常数kHy,从而式(12)可以转换为简化表达式如下:

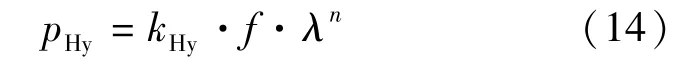
即磁滞损耗与磁链的关系函数,而磁链是可以通过测量的电气量计算得到,对于指数n而言,一般电机常用的铁磁材料为1.5～2.5[17]。

类似的,涡流损耗pEC的计算式[17]:

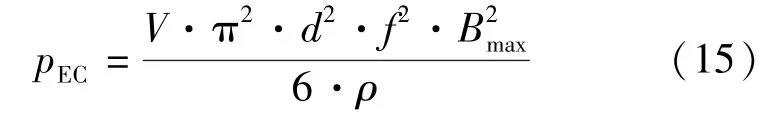
式中:d为磁性材料厚度;ρ是磁性材料的电阻率。同样引入涡流损耗系数kEC,可以简化式(15),具体如下:

将式(14)和式(17)合并,可以得到铁损模型的表达式如下:

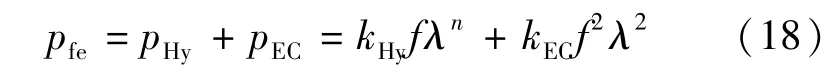
通过标准的电机空载试验可以定量地获得电机的铁损[17]。标准空载测试中,可以得到总的铁损和施加电压的函数关系,然后基于测试得到的铁损值进行拟合计算,就可以得到式(18)中的相关参数。考虑到一次标准空载试验只能给出对应测试频率点的铁损,因此除了额定频率点以外,还进行了更低转速时4个频率点的空载测试以获得更好的铁损模型描述。图4为频率点分别为10 Hz,20 Hz,30 Hz,40 Hz,50 Hz的空载试验测试结果。利用试验结果并

图4 电机空载铁损测试结果

结合表1中具体的电机额定参数,可以计算得到:kHy=1.591,kEC=0.017 8,n=1.432。根据式(18)可以计算出在图4中对应给定频率点和磁链的Rfe,此外铁损模型还可以用于在线估计IM铁损。

表1 IM额定参数

3 基于定子磁链模型的MEPT算法

对于一个给定的电机稳态工作点,包括固定的转矩,转速和电机温度,MEPT算法的目标是获得对应电机最大效率的最佳定子磁链λMEPT。

MEPT算法需要使用的电机参数包括电机定转子漏感Lls和Llr,激磁电感Lm,定转子电阻Rs和Rr,以及铁损等效电阻Rfe。其中对于给定电机温度下的电机参数可以从传统的空载和堵转试验中得到,但还需得到Lm随着激磁电流im变化的关系,参考图3和式(7),im近似等于i'd,最大激磁电流即空载试验中最大允许d轴电流Id,max。

3.1 d-q坐标系下的电流映射和模型求解

图5为转子磁链旋转d-q坐标系下第一象限内的电流映射区,定子电流的幅值在0～Imax之间,其中Imax为过载电流幅值限制,电流映射区构成了一个m×n的矩阵,其中电流矢量可以描述:

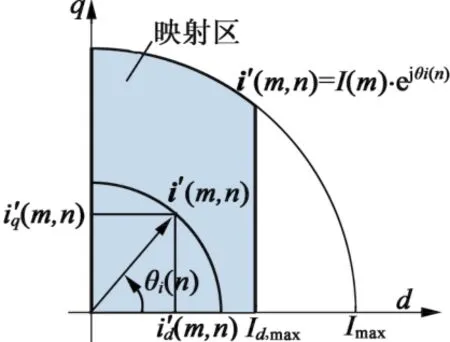
图5 d-q坐标系下的电流映射

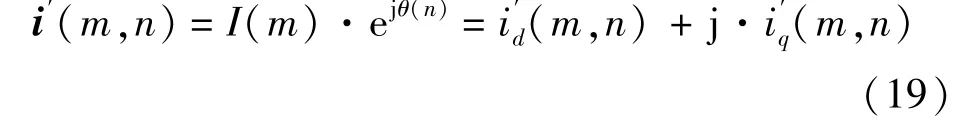
从图5中还可以看出,电流映射区中电流的位置跨度在最小值和90°电角度之间。而这个最小值也不是固定的,但是通常避免d轴电流高于Id,max。对于给定的电流矢量可以由式(2)的计算结果减去漏磁后得到定子磁链。对于式(2)中的激磁电感,采用的是如图6所示的)关系曲线,它是考虑磁饱和后根据式(7)计算得到的,根据图6,激磁电流峰值设置为6 A,额定值设置为3.5 A。计算完定子磁链以后,电机的电磁转矩和滑差转速可以分别通过式(4)和式(6)计算得到。对于一个给定的机械转速,电转速可以通过式(5)计算,从而反电动势和总定子电流,以及给定电机温度下的电机损耗和效率可以分别通过式(3)和式(8)～式(11)计算得到。

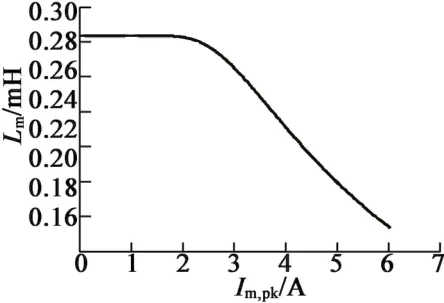
图6 Lm和Im,pk的关系曲线

3.2 最优定子磁链计算

对于给定的定子电流幅值I(m),电流矢量 的相位角θi(n)在电流映射是变化的,而最优定子磁链计算可以通过以下两种途径实现:

(1)MTPA方法:文献[10]中给出了具体的计算过程,该方法通过最大转矩来确定最优磁链λMTPA(m)。λMTPA(m)不和电机温度以及转速相关,而仅仅由磁饱和模型决定。

(2)MEPT方法:对于给定的转速和负载转矩,最优磁链λMEPT(m)能够通过对铁损的计算而选取使效率最优的结果得到。

通过以上两种方法可计算所有在0～Imax之间的m个点的结果。考虑到基于MEPT方法的磁链计算结果同时取决于电机温度和转速,因此还需要在不同电机温度下进行最优磁链计算。

3.3 计算结果

根据表1的电机参数和图6的Lm和Im,pk的关系曲线,采用前述MEPT计算方法可以得到不同转速下(1 400 r/min,1 000 r/min和500 r/min)的分析结果,具体如图7～图9所示,其中电机温度为40℃。为了对比,图7～图9中还绘出了额定磁链下的计算结果。从图中可以看出,在额定转矩以下,效率的改善是非常明显的。图10和图11为电机温度分别为40℃和75℃时的不同转速下的电机效率计算结果。从图10和图11中可以看出,不同温度和不同转速下在额定转矩15 N·m下,MEPT算法下的电机损耗明显降低,而根据图11,在转矩7.5 N·m时,效率可以提高6%,转矩5 N·m时,效率可以提高10%。而对于转矩大于额定转矩的情况,效率提高则较为有限。

图7 不同转矩下的MEPT算法计算结果(1 400 r/min和40℃)

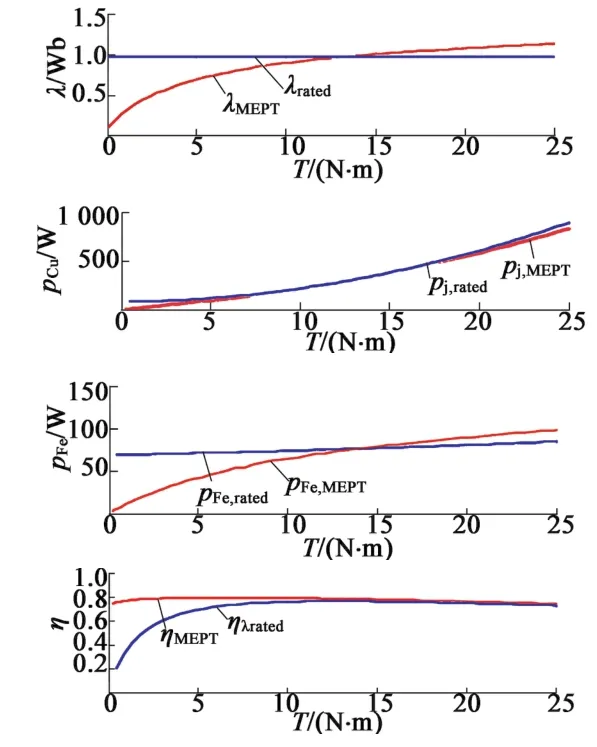
图8 不同转矩下的MEPT算法计算结果(1 000 r/min和40℃)

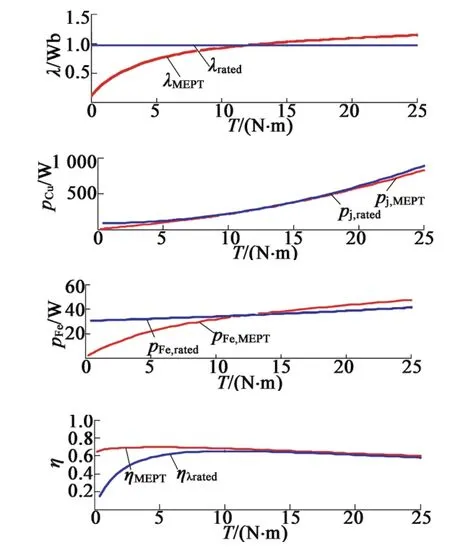
图9 不同转矩下的MEPT算法计算结果(500 r/min和40℃)

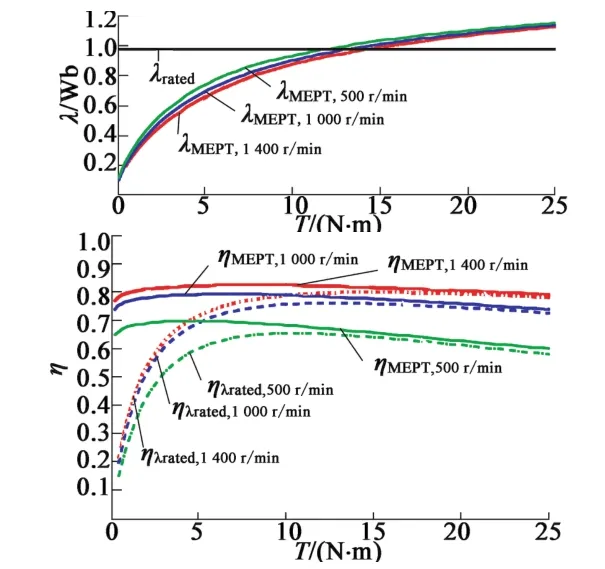
图10 不同转矩和转速下的MEPT算法计算结果(40℃)

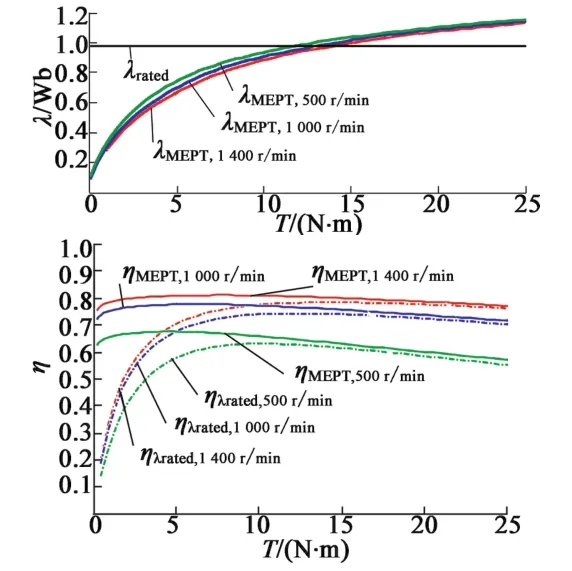
图11 不同转矩和转速下的MEPT算法计算结果(75℃)

4 DFVC控制策略

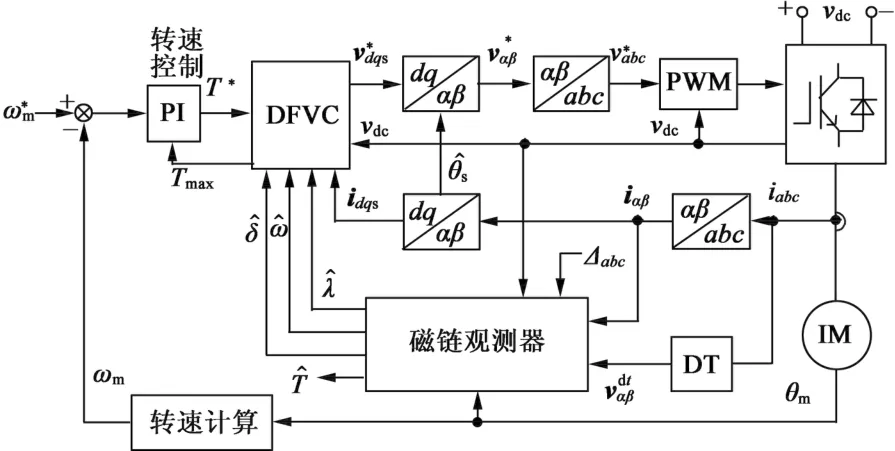
图12 IM新型控制方案框图

图12为IM驱动控制器整体框图。控制器是按照调速模式设计的,首先是转速外环,转速PI调节器输出参考转矩T*给DFVC模块,而转速PI调节器的最大参考转矩则是DFVC模块生成的,此外还有磁链观察器的输出和测量得到的输出电流,以及直流电压也给到DFVC模块进行运算,DFVC模块的具体的结构框图如图13所示。从图中可看出DFVC控制是一种混合控制方案,它是直接磁链控制和电流矢量控制的结合。具体而言,定子磁链是直接由ds轴电压分量控制,不受到qs轴分量的影响。磁链闭环控制的带宽设置较高,即合理设定PI调节器的比例增益使其不受到磁饱和影响。转矩完全由qs轴电流控制,PI调节器的输出为qs轴电压参考。从图13中还可以看出,参考磁链是由MEPT算法模块给出的,该模块根据输入的转矩需求和电机转速查询计算得到使效率最高的磁链参考,然后经过磁链限幅环节后送入到PI调节器,以及用于qs轴电流限幅的计算。DFVC模块输出电压控制参考后经过逆旋转坐标变换后经由PWM生成模块生成控制脉冲给到变频器实现最后的电机功率驱动。

图13 DFVC模块框图

5 试验验证

为了验证新型效率优化控制策略,基于2.2kW IM和永磁伺服电机构建模拟试验平台,IM参数见表1,具体的试验平台如图14所示。在IM转子上安装转矩传感器以测量转矩,用于评估机械输出功率。IM的驱动变频器输入直流电压为580 V,开关频率设置为 10 kHz。控制算法采用 dSPACE(DS1104)数字控制器实现。IM输入电功率和输出机械功率采用功率分析仪Zimmer(LMG500)测量。

图14 IM驱动试验平台

图15为分别在转速为500 r/min,1 000 r/min和1 400 r/min下测量得到的MEPT算法和额定磁链算法时的转矩效率试验曲线,电机温度为40℃。从图15中可以看出,和传统算法相比,MEPT算法在低转矩时明显提高了电机驱动效率。

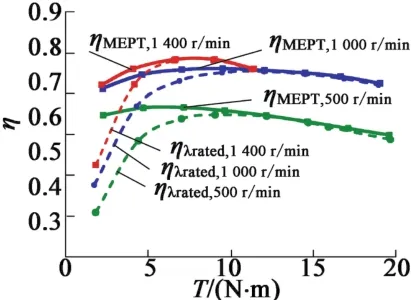
图15 不同转矩和转速下的MEPT算法试验结果(40℃)

图16为电机转速在1 000 r/min时测量得到的MEPT算法、MTPA算法和额定磁链算法时的转矩效

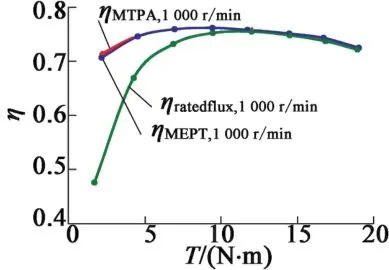
图16 MEPT算法和MTPA算法试验结果对比(40℃)

率试验曲线,电机温度为40℃。从图16中可以看出,MEPT算法和MTPA算法相比,在转矩小于5 N·m时,MEPT算法下的电机驱动效率要稍好于MTPA算法,进一步验证了MEPT算法的优势。

6 结 语

本文以提高IM在轻载运行的效率为目标,设计了一种基于直接磁链矢量的MEPT算法,通过理论推导计算和试验研究,可以总结出主要结论如下:

(1)MEPT算法中的最优磁链计算是基于铁损模型和查询表,铁损模型考虑了磁饱和效应,而参数是基于电机空载试验和堵转试验得到的。此铁损模型还可以用于在线损耗估计。

(2)试验研究表明,和传统算法相比,MEPT算法能够在IM低转矩运行时明显提高系统运行效率,且通用性更好,更易于工程实现。

参考文献

[1] 孟昕元,范峥.基于事实搜索方法的三相感应电机节能控制研究[J].微特电机,2016,44(8):76-78.

[2] 刘艳,张沾沾.感应电动机驱动系统的效率优化控制研究[J].微特电机,2016,44(2):67-70.

[3] 顾德军,李光耀,汤惠明,等.高压高效率三相异步电动机的开发[J].电机与控制应用,2015,42(5):81-84.

[4] 张兴华,孙振兴,王德明.电动汽车用感应电机直接转矩控制系统的效率最优控制[J].电工技术学报,2013,28(4):255-260.

[5] 赵海森,王博,王义龙,等.势能负载条件下感应电机变频-调压分段节能控制策略研究[J].中国电机工程学报,2015,35(6):1490-1497.

[6] 苗敬利,黄远.基于逐层预测模型的感应电机效率优化滑模控制[J].电工技术学报,2014,29(3):206-212.

[7] ABRAHAMSEN F,BLAABJERG F,PEDERSEN K J,et al.Efficiency-optimized control of medium-size induction motor drives[J].IEEE Transactions on Industry Electronics,2001,37(6):1761-1767.

[8] ABRAHAMSEN F,BLAABJERG F,PEDERSEN K J,et al.On the energy optimized control of standard and high efficiency induction motors in CT and HVAC applications[J].IEEE Transactions on Industry Applications,1998,34(4):822-831.

[9] WASYNCZUK O.A maximum torque per ampere control strategy for induction motor drives[J].IEEE Transactions on Energy Converters,1998,13(2):163-169.

[10] 俞荣凯,赵坤,游小杰,邵闻博.异步电机最大转矩电流比控制方法研究[J].电力电子技术,2008,42(7):33-34.

[11] SUNG W,SHIN J,JEONG S Y.Energy-efficient and robust control for high-performance induction motor drive with an application in electric vehicles[J].IEEE Transactions on Vehicle Technology,2012,61(8):3394-3405.

[12] KIRSCHEN S D,NOVOTNY W D,LIPO A T.Optimal efficiency control of an induction motor drive[J].IEEE Transactions on Energy Converters,1987,2(1):70-76.

[13] EBRAHIM S O,BADR A M,ELGENDY A S,et al.ANN-based optimal energy control of induction motor drive in pumping applications[J].IEEE Transactions on Energy Converters,2010,25(3):652-660.

[14] 王宝忠,要丹,孙健涛.感应电机无速度传感器直接转矩控制的智能优化设计[J].电机与控制应用,2011,38(12):27-31.

[15] 王晶鑫,姜建国.矩阵变换器驱动感应电机转矩和转子磁链控制[J].电机与控制学报,2010,14(7):59-65.

[16] 刘新正,苏少平,高琳.电机学[M].北京:电子工业出版社,2014.

[17] 黄坚,郭中醒.实用电机设计计算手册)[M].2版.上海:上海科学技术出版社,2014.