风险规避下基于联合促销的供应链协调研究
2017-05-15汪峻萍
汪 亚, 汪峻萍
(合肥工业大学 数学学院,安徽 合肥 230009)
风险规避下基于联合促销的供应链协调研究
汪 亚, 汪峻萍
(合肥工业大学 数学学院,安徽 合肥 230009)
文章针对随机需求受联合销售努力影响情形,分别在加和与乘积2种需求形式下,建立了由风险规避零售商与风险中性制造商组成的供应链协调模型,据此分析了风险规避对最优决策以及协调契约的影响。研究结果表明:2种需求形式下风险规避对销售努力的影响是不同的,在加和形式下零售商的最优订购量随着风险规避程度的增大而减少,零售商和制造商的最优促销努力却与风险规避无关;在乘积形式下零售商的最优订购量、最优促销努力以及制造商的最优促销努力均随着风险规避程度的增大而减少。此外,在加和形式下可以设计由回购契约与成本共担契约所组成的混合契约来实现供应链协调;在乘积形式下可以设计利润共享契约来实现供应链协调。
风险规避;联合促销;回购契约;加和需求形式;乘积需求形式
随着科学技术的飞速发展,越来越多的新产品涌入市场,促使零售商和制造商不得不通过做广告、货架展示、培训以及雇佣更多营销人员等途径来增加销售量,降低产品库存。销售努力对供应链协调问题的影响一直是供应链管理研究的热点之一。随着市场的不确定性逐渐增大,供应链成员对于利润的敏感性也开始逐渐增强。供应链上下游企业开始重视风险,并通过一定的策略躲避风险。相关实证研究表明,供应链成员风险规避态度已成为影响其决策行为的重要因素[1-2]。
将风险规避和销售努力引入供应链中的相关文献研究大致可以分为2类。第1类研究只考虑风险规避或销售努力。例如,文献[3]在随机需求下考虑了由风险中性的制造商和以CVaR作为风险度量的风险规避零售商所组成的两级供应链模型,并将该模型作为一个纳什均衡问题进行研究分析;文献[4]对回购合约和期权合约在风险中性和风险规避2种假定下零售商和制造商的决策进行了比较;文献[5]对市场需求受零售价格和制造商努力线性影响且零售商处于领导地位的两级供应链进行求解并协调;文献[6]对需求同时受零售商和制造商努力影响下,对两部关税契约能否协调以及如何协调供应链进行分析研究。第2类研究同时考虑了销售努力和风险规避,但是只考虑零售商单方销售努力或考虑供应链成员联合促销且只考虑一种受销售努力影响的需求模式。例如,文献[7]研究了风险规避的零售商且需求与零售商努力满足乘积形式时的供应链,考虑了风险规避对销售努力的影响;文献[8]考察风险规避的零售商和风险中性的制造商联合促销的供应链回购契约协调问题;文献[9]求解基于CVaR准则风险规避的零售商,此外还研究了需求与联合广告投入满足相乘形式时的供应链中的最优广告投入及订货策略。
本研究同时考虑了风险规避与供应链成员联合促销努力,分别在加和与乘积2种不同需求形式下,建立了由风险规避零售商与风险中性制造商组成的供应链协调模型。
1 模型假设
本文考虑的是由一个风险中性的制造商和一个风险规避的零售商组成的两层供应链,制造商和零售商之间是动态的Stackelberg博弈,制造商为博弈的领导者,零售商为追随者。在一个销售季节初,制造商根据市场情况和产品的成本价c与零售商协商签订回购合同{w,b},即制造商以批发价格w向零售商提供产品,为激励零售商多订货,制造商在销售期末会对零售商的剩余产品进行回购,回购价格为b。零售商根据市场需求D和回购合同决定其订购量Q,而零售价p是由市场决定的。与此同时,为了刺激市场需求,增加订购量,制造商和零售商同时做出促销努力分别为em和er,如广告投入、销售人员培训等,以激励消费者购买,增加自身的收益。为排除一些不必要的讨论,假定p>w>c,且b≤w。
根据上述问题的描述与假设,商品市场需求D既受到供应链成员联合促销努力的影响,也受到不确定因素的影响。而销售努力水平一般以2种方式影响需求:一是加和形式,即D(e)=y(e)+ξ[10];二是乘积形式,即D(e)=y(e)ξ[11],其中假定y(e)为关于努力水平单调递增的凹函数;ξ为需求中的随机变量,其分布函数和密度函数分别为F(ξ)和f(ξ),均值为μ。假设F是连续可微、严格递增,且F(0)=0。因此,根据零售商和制造商联合促销努力,采用上述2种需求形式,可得加和与乘积形式下市场需求分别为:
D(er,em,ξ)=α+krer+kmem+ξ=y(er,em)+ξ;
D(er,em,ξ)=(α+krer+kmem)ξ=y(er,em)ξ
(1)

2 两种需求形式的分散决策模型
在分散决策下,风险规避的零售商需要面对市场的不稳定性,制造商只是根据零售商订单进行供货,因而不需要承担风险,因此不考虑制造商的风险规避,即制造商是风险中性的,根据Stackelberg博弈的主从关系,先对零售商的最优决策进行求解分析,再求出制造商的最优决策。
2.1 加和形式下的分散决策模型
由于零售商是风险规避的,为解出最优决策,本文拟建立零售商的风险规避效用函数,参照文献[4]和文献[13],用η表示零售商的损失风险规避系数,同时考虑缺货损失规避与库存损失规避,规避系数均为η(η∈[0,1]),η越大,风险规避程度越高。当η=0时,零售商是风险中性的。由模型假设知期望销售为:
S(Q,er,em)=Emin(Q,D(er,em,ξ))=

(2)
期望剩余库存为:
I(Q,er,em)=E(Q-D(er,em,ξ))+=
Q-S(Q,er,em)
(3)
期望缺货量为:
L(Q,er,em)=E(D(er,em,ξ)-Q)+=
μ+y(er,em)-S(Q,er,em)
(4)
则分散决策下零售商的效用函数为:
U(πr)=pS(Q,er,em)+bI(Q,er,em)-
η(p-b)I(Q,er,em)-
(5)
(6)
定理1 在零售商风险规避下,零售商的最优订购量、最优促销努力及制造商的最优促销努力分别为:
(7)
(8)
(9)



证明 由(8)式和(9)式可知:

由(7)式可知:


(10)

推论1说明随风险程度的增大,零售商为躲避损失风险或剩余风险会减少订购量,但零售商和制造商的销售努力却与风险规避系数无关。这是由于对于一些市场知名度比较高的成熟品牌产品,客户需求相对来说比较稳定,即“目标客户”相对稳定,市场份额的波动性不会太大,损失风险或剩余风险相对来说很小,零售商和制造商的风险规避对销售努力的影响可以忽略不计。推论1也说明了加和需求形式适用于知名度较高的品牌产品供应链。

证明 由(8)式和(9)式可知:

由(10)式可知:

(11)

由(8)式和(9)式知:

推论2说明回购价格越高,越激励零售商增加订购量来获取更高的利润,但是此时的促销努力对市场需求影响不是很大,这是因为在增加订购量的同时,为降低促销成本,双方都不再做促销努力;批发价格越大,零售商在风险作用下,会减少订购量,同时减少促销努力降低成本,但对于制造商,它会通过增大促销努力来增加市场需求量,刺激零售商多订购,增加自身的利润收益。
2.2 乘积形式下的分散决策模型
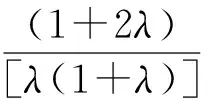

(12)
I(Q,er,em)=Q-S(Q,er,em)
(13)
L(Q,er,em)=μ·y(er,em)-S(Q,er,em)
(14)
分散决策下零售商的效用函数、制造商的期望利润分别为:
U(πr)=pS(Q,er,em)+bI(Q,er,em)-
λ(p-b)I(Q,er,em)-
(15)
(16)
在乘积随机需求形式下,求解模型的最优解与加和形式下的求解方法相似,由此可得零售商的最优订购量、最优促销努力以及制造商的最优促销努力分别为:
(17)

(18)
(19)


(20)

由(19)式得:

(21)

由(10)式知:
(22)
推论3说明风险规避程度越大,零售商为躲避损失或者剩余风险会降低订购量。零售商和制造商的销售努力随着风险规避程度的增大而减少,且在实际中也能找到匹配的对象。比如,新产品或品牌知名度较低的产品的市场占有率相对较小,因为广告宣传可以诱导和激励潜在顾客的购买行为,所以利用广告、增加营销人员等销售努力可以显著提高市场需求,迅速扩大市场份额。零售商和制造商的风险规避程度增加时,需求越高,意味风险越大。因此为躲避风险,零售商和制造商都会采取降低促销努力缩小市场需求,有效降低风险。推论3也说明了乘积需求形式适用于新产品或品牌知名度较低的产品供应链。

证明 当随机需求量ξ服从均匀分布ξ~U[0,a]时,有:

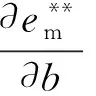
(23)
(24)

(25)
(26)

与推论2相似,但在乘积形式需求下推论4的促销努力均受回购价格影响,因为促销努力受风险程度的影响,使市场需求发生变化,所以回购价格越高,双方通过增大促销努力以扩大市场需求获得更高的利润。综观推论2和4可以看出,从制造商的角度来看,可通过调整契约参数,使零售商的订购决策和促销努力按制造商意欲方向发生变化。
3 两种形式的集中决策模型及协调
在实际的生产活动中,因为风险规避的零售商和风险中性的制造商需要从供应链系统的整体利润出发,而且目标是实现供应链整体的最优化,即实现供应链整体的期望利润最大化,所以在集中决策下可以不考虑此时零售商的风险规避性,把制造商和零售商看成隶属同一个公司,同时也不必考虑制造商和零售商之间的利润分配问题,因此本文采用风险中性下的集中决策模型。对于含有风险规避的零售商的供应链中,有很多学者在集中模式决策下采用风险中性供应链并没有考虑风险[8,11,14-16]。
3.1 加和形式的集中决策模型及契约协调
在加和形式需求下,可得供应链系统期望利润为:
πs(Q,er,em)=pS(Q,er,em)-
易验证供应链系统利润πs(Q,er,em)关于Q、er、em的Hessian矩阵是负定的,因此求解一阶性最优条件得:
(27)
(28)
(29)
定理2 传统的回购契约不能协调联合促销的供应链。

由于传统回购契约不能协调联合促销的供应链,下面考虑引入成本共担来修正契约,即在{w,b}基础上,供应链成员互相分担成本。考虑由回购契约和成本共担契约所组成的混合契约{w,b,t,θ},即制造商(零售商)承担自己促销成本t(θ)部分,分担对方促销成本1-θ(1-t)部分,t,θ∈[0,1],则在此契约基础上可得:
U(πr)=pS(Q,er,em)+bI(Q,er,em)-
η(p-b)I(Q,er,em)-η(p-w)L(Q,er,em)-

(30)
πm=(w-c)Q-bI(Q,er,em)-
(31)

(32)
(33)
(34)
定理3 存在一个临界值ηr=c/(p-2c),当η>ηr时,契约{w,b,t,θ}不能协调供应链;当η≤ηr时,存在无穷多个{w,b,t,θ}契约可以协调上述供应链,其中参数满足以下条件:


(35)
其中,0 于是η≤c/(p-2c)。 由(29)式、(34)式,又联合(27)式、(32)式可得:p-w=θ(p-c),又由(28)式、(33)式得p-w=(1-t)(p-c),即1-t=θ,也即零售商承担自身的促销成本与制造商承担零售商的促销成本比例相同。 定理3说明了供应链的协调能否实现取决于零售商风险规避程度的临界值ηr,这一临界值可由商品的价格、生产成本等外生变量决定。 3.2 乘积形式的集中决策模型及契约协调 在乘积形式需求下的集中决策,参照3.1节也易验证供应链系统利润πs(Q,er,em)关于Q、er、em的Hessian矩阵是负定的,因此求解一阶性最优条件,联合可得: (36) (37) (38) 其中,Θ=F-1[(p-c)/p]。 在集中决策下,系统的期望利润达最优,但对其他成员来说不一定最优,因此有必要设计一个行之有效的契约,使供应链中各成员愿意采取集中决策下的最优策略,实现供应链系统的利润最大化。本文采用利润共享契约[17-19]来协调供应链,在此契约下供应链成员通过协商、谈判决定利润分配,从而实现“共赢”。本文将从制造商和零售商风险偏好的效用角度对利润分配比例取值做讨论。 令Δπm、Δπr分别表示与分散决策下期望利润相比,该契约给制造商、零售商所带来的收益,定义Um(Δπm)、Ur(Δπr)分别为制造商、零售商的效用函数,并定义相对风险规避系数为: (39) 假定制造商、零售商都是风险规避的,且效用函数为: Um(Δπm)=-e-amΔπm,Ur(Δπr)=-e-arΔπr (40) 其中,am、ar均为正常数。 由(39)式可知,制造商和零售商都有着常数相对风险规避度,且有: Rm(Δπm)=am,Rr(Δπr)=ar (41) 在该契约下所带来的供应链系统总效用为: Us(Δπm,Δπr)=Um(Δπm)+Ur(Δπr)= bm(-e-amΔπm)+br(-e-arΔπr) (42) 其中,权重系数bm、br分别为制造商与零售商的谈判能力,且bm+br=1。 由于Δπs=Δπm+Δπr,故(42)式可写成: Us(Δπr)=bm(-e-am(Δπs-Δπr))+br(-e-arΔπr), 对Us(Δπr)关于Δπr求一阶偏导并令其为0,可得: -bmame-am(Δπs-Δπr)+brare-arΔπr=0 (43) 由(43)式知,在考虑供应链成员风险偏好的情形下,利润共享契约给制造商和零售商带来的期望利润分别为: (44) Δπm=Δπs-Δπr=(1-s)Δπs+ω (45) 综上可知:① 零售商和制造商的系统增加利润分配比例只与各自相对风险规避系数有关,而与其权重无关,若供应链中参与成员的相对风险规避系数越高,则该成员所获得的系统增加利润就越少;② 供应链中补偿利润的大小不仅取决于各成员的相对风险规避系数,而且还取决于各自的权重系数,特殊地,当各成员的相对风险规避系数相等时,此时获取还是付出补偿利润取决于供应链中各成员讨价还价的能力,若讨价还价的能力强,则可获取相应的补偿利润。 下面通过数值仿真计算进一步对本文得出的结论进行说明与验证,假设随机变量ξ服从均匀分布U[0,100],y(er,em)=100+5er+4em,p=20,c=5,β=γ=2。 表1 风险规避系数η或λ对变量的影响 由表1可知,在加和需求形式下,零售商的订购量随着风险程度的增大而减少,而双方的促销努力均不受风险的影响,说明加和形式适用于知名度较高的品牌产品供应链;在乘积需求形式下,促销努力、订购量都随风险程度的增加而减少,说明乘积形式更加适用于新产品或品牌知名度较低的产品供应链,且零售商的促销努力及订购量下降的速度极快,即它们与风险程度有直接联系。 表2 不同契约安排下的促销努力与订货策略 对于乘积需求形式下的供应链协调,利用利润共享契约使供应链协调,根据上述参数与分散决策下相比,供应链系统增加的期望利润为Δπs=2 976 617.1,则在此契约下供应链成员相对风险规避系数对利润分配比例的影响见表3所列。 表3 am、ar对系统增加利润分配比例的影响 由表3可知,如果供应链任一成员的风险规避系数越大,那么该成员所分配的系统增加的期望利润就越少;相反其余成员所分配的系统增加的期望利润就越多,这意味着供应链中各成员都会在实际的商业运作中尽量减小风险规避度;由数据模拟进一步证实了当ω为负值时,制造商将会给零售商一定的补偿利润。因此,在实际生活中,制造商为了避免支付补偿利润,会增加自身的权重系数,即加强讨价还价能力。 本文在随机需求受联合销售努力影响的加和与乘积2种需求形式下,运用回购契约对风险规避的零售商与风险中性的制造商组成的供应链建立相应的模型,进行求解、分析及协调供应链,探讨风险规避对最优决策以及回购契约参数的影响,并得到了结论及相应的管理启示。本文只研究了基于供应链成员一方是风险规避,对供应链双方都风险规避,且集中决策下是否也具有风险规避,能否继续进行协调供应链,或者在风险偏好的基础上能否引入其他行为偏好,将是今后进一步研究的方向。 [1] GAN X H,SETHI S P,YAN H M.Coordination of supply chains with risk-averse agents[J].Production and Operations Management,2004,13(2):135-149. [2] TSAY A A.Risk sensitivity in distribution channel partnerships:Implications for manufacturer return policies[J].Journal of Retailing,2002,78(2):147-160. [3] MA L J,LIU F M,LI S J,et al.Channel bargaining with risk-averse retailer[J].International Journal of Production Economics,2012,139(1):155-167. [4] 程永文,周永务.风险规避假定下对回购策略以及期权策略的不同影响[J].系统工程理论与实践,2013,33(4):861-869. [5] WEI X.Coordination and incentives in a supply chain with manufacturer quality effort[C]//2014 26th Chinese Control and Docision Conference(CCDC).[S.l.:s.n.],2014:3557-3561. [6] MA P,WANG H Y,SHANG J.Contract design for two-stage supply chain coordination:Integrating manufacturer-quality and retailer-marketing efforts[J].International Journal of Production Economics,2013,146(2):745-755. [7] SUO H S,WAND J C,JIN Y H.Supply chain coordination with sal-es effort effects and impact of loss aversion on effort decision[J].Tsinghua Science and Technology,2005,10(1):102-107. [8] 代建生,孟卫东.基于CVaR的供应链联合促销的回购契约协调研究[J].中国管理科学,2014,22(7):43-51. [9] 张丽娜,刘桂庆,林冠男.利润-CVaR准则下供应链中的联合广告投入与订货策略研究[J].合肥工业大学学报(自然科学版),2015,38(2):258-263. [10] LARIVIERE M A,PORTEUS E L.Selling to the newsvendor:an analysis of price-only contracts[J].Manufacturing & Service Operations Management,2001,3(4):293-305. [11] TAYLOR T A.Supply chain coordination under channel rebates with sales effort effects[J].Management Science,2002,48(8):992-1007. [12] XIAO T J,YANG D Q.Risk sharing and information revelation mechanism of a one-manufacturer and one-retailer supply chain facing an integrated competitor[J].European Journal of Operational Research,2009,196(3):1076-1085. [13] SCHWEITZER M E,CACHON G P.Decision bias in the newsvendor problem with a known demand distribution:experimental evidence[J].Management Science,2000,46(3):404-420. [14] GAN X H, SETHI S P, YAN H M.Channel coordination with a risk-neutral supplier and a downside-risk-averse retailer[J].Production and Operations Management Society,2005,14(1):80-89. [15] 安勇.CVaR准则下需求受到努力水平影响的供应链回购契约[J].物流技术,2012,31(6):94-97. [16] 简惠云.基于风险和公平偏好的供应链契约及其实验研究[D].长沙:中南大学,2013. [17] 王圣东,汪峻萍.易逝品供应链协调理论与方法[M].合肥:中国科学技术大学出版社,2012:30-31. [18] LI Y.Supply chain modeling:price,contract and coordination[D].Hongkong:The Chinese University of Hong Kong,2002. [19] JABER M Y,OSMAN I H.Coordinating a two-level supply chain with delay in payment and profit [J].Computers & Industrial Engineering,2006,50(4):385-400. (责任编辑 万伦来) Study of risk-averse supply chain coordination based on combined promotion efforts WANG Ya, WANG Junping (School of Mathematics, Hefei University of Technology, Hefei 230009, China) By assuming that the stochastic demand is influenced by combined sales efforts, a supply chain coordination model with a risk-averse retailer and a risk-neutral manufacturer is established under the addition and multiplication demand forms, respectively. The influence of risk aversion on the optimal decision and coordination contract is discussed. The results show that the influences of risk aversion on the sales efforts are different between the two demand forms; under the addition form, the retailer’s optimal order quantity decreases with the increase of risk aversion, the optimal promotion efforts of retailer and manufacturer are not related to the aversion, while the retailer’s optimal order quantity, the optimal sales promotion efforts of retailer and manufacturer decrease with the increase of risk aversion under the multiplication form. Under the addition form, a combined contract of buy back contract and cost sharing contract is designed to coordinate the supply chain; under the multiplication form, however, a profit sharing contract is designed to achieve supply chain coordination. risk averse; combined promotion efforts; buy back contract; addition demand form; multiplication demand form 2015-12-16; 2016-05-09 安徽省自然科学基金资助项目(1508085MG141);合肥工业大学博士专项基金资助项目(JZ2015HGBZ0503) 汪 亚(1991-),女,安徽亳州人,合肥工业大学硕士生; 汪峻萍(1975-),女,安徽黄山人,博士,合肥工业大学副教授,硕士生导师. 10.3969/j.issn.1003-5060.2017.04.024 F253.4 A 1003-5060(2017)04-0559-08



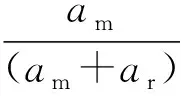
4 数值仿真分析
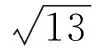




5 结 论
