Halbach 阵列永磁同步直线电机边端力最小化研究

王斐然，廖有用，陈进华，张 驰，罗 均

(1.中国科学院宁波材料技术与工程研究所,宁波315201;2.上海大学,上海200072)

0 引 言

永磁直线电机(以下简称PMLSM)兼具永磁电机和直线电机的双重特点。与电励磁直线电机相比,PMLSM力密度高、损耗小、结构简单,在电磁推力、效率和定位精度等方面具有明显优势。特别是随着Nd-Fe-B永磁材料性价比的提高,在很多应用场合下,PMLSM具有更加广阔的应用前景[1]。

针对PMLSM由于初级铁心开端而产生的端部效应,国内外学者做了大量的研究工作。文献[2]针对PMLSM建立了由于边端效应产生的磁阻力分析模型,运用傅里叶级数的方法对磁阻力进行了分析,提出了优化初级长度从而降低磁阻力的方法。但是其结果并不适用于本文中的电机模型。文献[3-4]先求出径向阵列永磁同步直线电机空载气隙磁场解析表达式,再用麦克斯韦张量法求出初级受到的边端力,并得出边端力最小时的初级长度。

本文在上述工作的基础上进行总结工作,使用两种方法对边端力最小时的初级长度进行求解。一方面,在文献[2]模型基础上,进行重新推导,得出最优初级长度。另一方面,用解析法求出Halbach阵列永磁同步直线电机气隙磁场表达式,并基于麦克斯韦张量法求解初级边端力,根据边端力解析式得出最优初级长度。并使用有限元法对最优初级长度进行验证,结果表明提出的最优初级长度是可行的,可以有效降低 PMLSM的边端力,从而抑制PMLSM的推力波动。

1 直线电机分析模型

图1为Halbach阵列PMLSM的磁力线分布,可见初级铁心两端附近磁场发生了畸变,这是端部效应产生的原因。

图1 PMLSM端部磁场畸变

由于直线电机有很多种类型,本文以一种单边无槽Halbach阵列永磁同步直线电机进行分析,分析计算所用的电机模型如图2所示。

图2 Halbach阵列永磁同步直线电机物理模型

该电机由初级部分和次级部分组成,初级部分由铁心和线圈绕组组成,次级部分由背铁和永磁体组成。初级采用无槽结构,有利于减小动子质量并降低推力波动。

沿y轴磁化的永磁体称为主永磁体,沿x轴磁化的永磁体称为副永磁体,永磁阵列充磁方向如图2所示。图2中,g为气隙高度,hm为永磁体高度,τp为主永磁体长度,τ为极距,μ0为空气磁导率。

2 基于傅里叶极数的边端力解析

根据文献[2],如图3所示的结构中,初级铁心受到的端部力为左右两端边端力之和。

图3 Halbach阵列PMLSM边端力模型

左右两端受到的力傅里叶表达式:

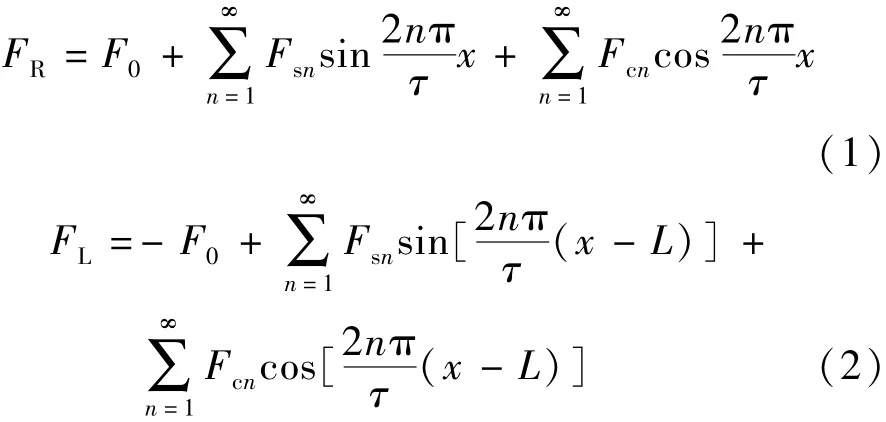
式中:L为动子铁心长度;τ为极距。

将式(1)、式(2)中的同频项合并,可得:

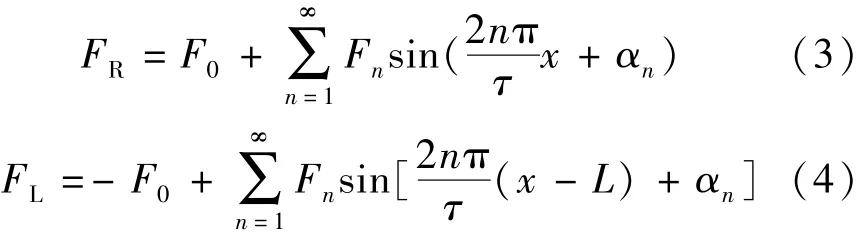
式中:

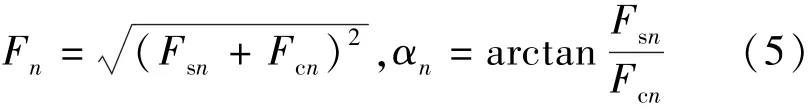
整个动子的端部力:

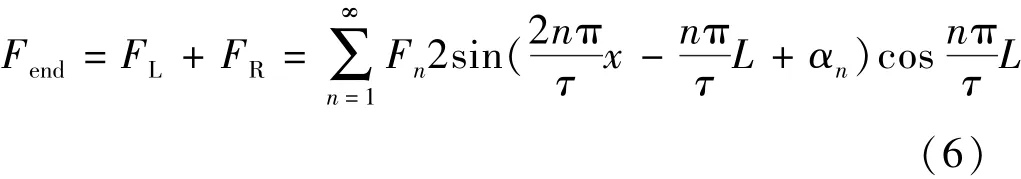
从式(6)可看出,要使边端力最小,只要满足:

式中:k为任意正整数。

3 基于麦克斯韦张量法的边端力解析

3.1 空载气隙磁场解析

本文以一种单边无槽Halbach阵列PMLSM为模型求解其磁场及边端力,如图2所示。

根据等效磁化强度法的原理,可将Halbach阵列永磁体作用等效为磁化强度函数M[5]。

式中:

则永磁体的等效面电流密度Jm:

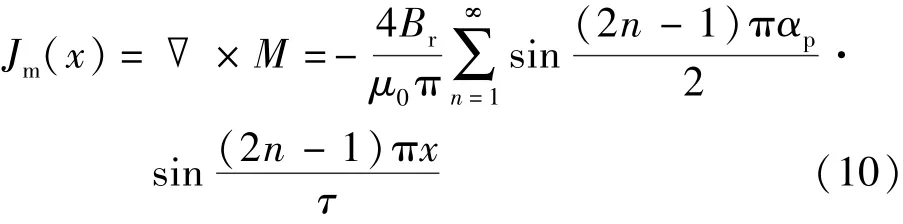
根据Maxwell方程组,引入矢量磁位函数A(x,y),可得:

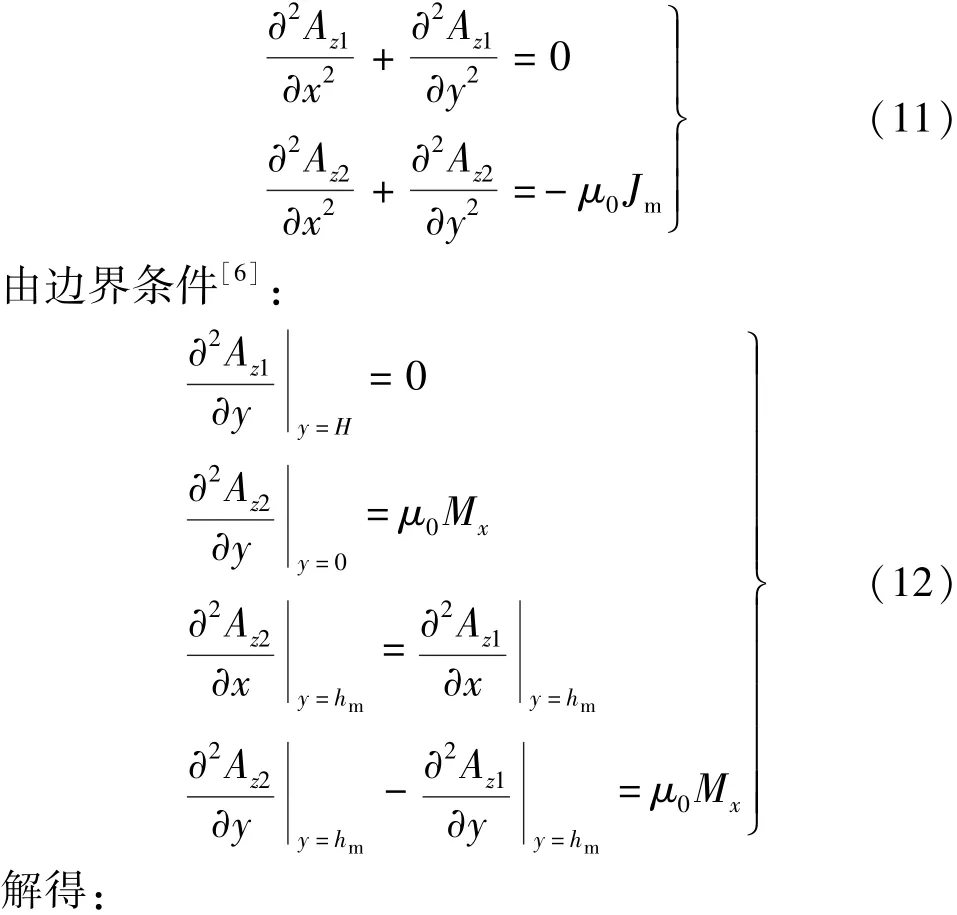
3.2 边端力解析

铁心结构如图3所示,其所受边端力[3-4]:

3.3 边端力特性分析

将kn代入式(17)中,可得[4]:

(1)式(16)的3项均为关于动子铁心中心的位移x0的周期函数,而且都有共同的周期T1=τ。

(2)当初级铁心的位移在0～τ内变化时,端部力与铁心长度有关,而且呈周期性变化,周期为T2=2τ,若仅考虑波动值的幅值,与铁心长度L也呈周期性变化,周期为T3=τ。

(3)端部力解析式中,第一项为各阶谐波之和,后两项为各阶谐波耦合项。首项对端部力有较大的幅值贡献,是端部力的主要成分。在L=(k+0.5)τ(k为任意正整数)时,cos(knL)=0,首项求和式为零,端部力有最小值。在L=kτ(k为任意正整数)时,cos(knL)=±1,首项求和式最大,端部力有最大值。

4 有限元验证

4.1 边端力特性有限元验证

上述解析的分析结果可以通过有限元进行验证。针对结构如图2所示,参数如表1所示,样机分别用解析法和有限元法进行求解。

表1 Halbach阵列PMLSM样机参数

(1)图4给出了初级铁心长度分别为88 mm,90 mm,92 mm时的端部力曲线。曲线反映了不同铁心长度值下端部力的基本周期均为1个极距。

图4 边端力与位移变化关系

(2)图5给出了端部力和铁心长度的周期性关系。当初级铁心的位移在0～τ内变化时,端部力的变化曲线在L=4τ=72 mm和L=6τ=108 mm时幅值和相位近似,与L=5τ=90 mm曲线幅值近似,相位相差约为180°;

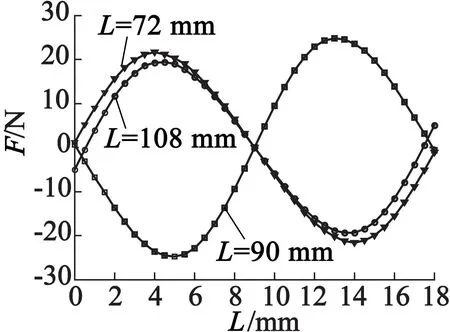
图5 边端力与初级长度的周期性关系

(3)图6给出了端部力波动的幅值和铁心长度变化关系。若仅考虑端部力的幅值变化,其与铁心长度L呈周期性变化,且基本在L=(k+0.5)τ(k为任意正整数)时,端部力有最小值,在L=kτ时,端部力有最大值。

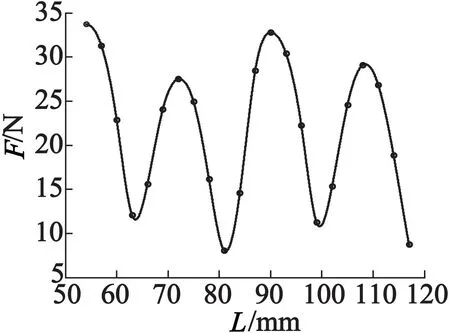
图6 边端力幅值与铁心长度变化关系

有限元分析与解析结果基本相符,存在一定的误差,误差的出现是因为边端力解析中,假设动子铁心的磁导率为无穷大、未考虑漏磁等原因所导致。

4.2 推力波动有限元验证

为了验证按照本文提出的最优初级长度下推力波动是否符合要求,按照图2的结构模型,表1的结构参数,选择初级长度为(4+0.5)×18=81 mm。在Ansoft Maxwell中构建模型并仿真,得到负载条件下的连续推力波动曲线如图7所示。

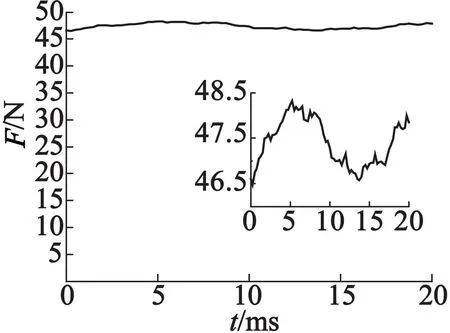
图7 连续推力波动曲线

由图7中数据算得,负载条件下的推力波动率为3.88%,符合工程要求。从而验证本文推出的最优初级长度能够有效抑制推力波动。

5 结 语

本文通过基于傅里叶极数的解析法推导出边端力最小时的PMLSM初级长度L=(k+0.5)τ(k为任意正整数),并通过磁场解析和麦克斯韦张量法求出Halbach阵列PMLSM边端力解析式,由边端力解析式再次推导出最优初级长度。最后,通过有限元验证上述解析法得到的结果,并求出推力波动率。结果证明,本文推导的最优初级长度能有效减小Halbach阵列PMLSM的边端力,从而抑制推力波动。

参考文献

[1] 闫阿儒,张驰.新型稀土永磁材料与永磁电机[M].北京:科学出版社,2014.

[2] 韩雪岩,祁坤,张哲,等.永磁同步直线电机磁阻力分析及抑制措施[J].电工技术学报,2015,30(6):70-76.

[3] 程远雄.永磁同步直线电机推力波动的优化设计研究[D].武汉:华中科技大学,2010.

[4] 张颖.永磁同步直线电机磁阻力分析及控制策略研究[D].武汉:华中科技大学,2008.

[5] 潘开林.永磁直线电机的驱动特性理论及推力波动优化设计研究[D].杭州:浙江大学,2003.

[6] 汤蕴璆,梁艳萍.电机电磁场的分析与计算[M].北京:机械工业出版社,2010.