直接转矩控制在空间微特电机中的应用研究
2017-05-13张沛,刘鑫
张 沛,刘 鑫
(北极空间飞行器总体设计部,北京100094)
0 引 言
在空间伺服控制系统中,永磁同步电机因为体积小,效率高等诸多优势,逐渐成为主流的空间微特电机。目前应用比较成熟的永磁同步电机驱动方法是空间矢量控制(以下简称SVPWM),虽然矢量控制可以实现永磁同步电机的解耦控制,使其具有类似直流电机的调速性能,但是矢量控制需要进行大量的坐标系转换,增加了控制算法的复杂度[1-2]。同时空间矢量控制算法必须在电机输出端增加位置传感器用以检测转子位置,从而增加了系统硬件的复杂度,降低了可靠性,不利于有严格重量限制和可靠性要求的空间伺服系统。
直接转矩的控制思路是把电动机与逆变器看作一个整体,通过估计定子磁链来对电动机的电磁转矩进行直接控制。由于不需要将定子电流投影到转子坐标系,从而免去了复杂的坐标转换,并可获得更大的瞬时转矩和更快的动态响应[3-5]。由于无需检测转子位置,因而无需安装旋转变压器,从而降低了系统成本,提高了系统可靠性,在空间伺服系统中具有广泛的应用前景。
传统的直接转矩控制方案是将定子磁链在整个调速范围内控制为圆形,幅值近似保持不变,同时需要根据定子磁链幅度估计电磁转矩,并进行电磁转矩的闭环控制。这种控制方法一方面由于需要估计电磁转矩,增加了算法的复杂度;另一方面由于需要给定定子磁链幅值,并且该给定值需要通过大量调试获得,因此降低了控制算法的适应性。文献[6-7]通过构造定子磁链降阶观测器估计转速进行转矩和磁链双闭环控制,减小了转矩脉动,但是增大了算法的复杂性。对于空间伺服控制系统而言,一方面由于电机输出端连接行星齿轮等减速器,对转速的波动并不敏感,另一方面空间飞行器的硬件计算资源有限,复杂的直接转矩控制方案并不适合于空间应用环境,因此有必要简化传统的直接转矩控制方案,并增强控制方案的鲁棒性,以适应空间微特电机控制的需求。
本文对传统直接转矩控制方案进行了简化,取消了转矩闭环,通过直接控制定子磁链幅值实现了转速闭环控制。仿真和带载测试结果验证了本文所提出的直接转矩控制方案的可行性和有效性。
1 直接转矩控制原理
1.1 永磁同步电机的数学模型
永磁同步电机在定子α-β坐标系下的电机电磁转矩表达式:
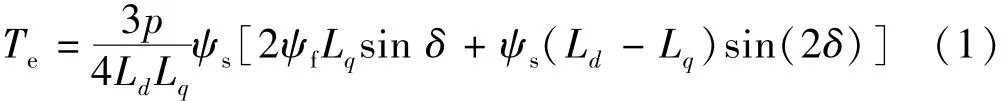
式中:δ为定子磁链和转子磁链之间的夹角;p为电机极对数;Ld为直轴电感;Lq为交轴电感;ψf为转子磁场幅度;ψs为定子磁链幅度。
对于空间环境中应用的隐极式永磁同步电机,

电磁转矩可看作转子磁场ψf与定子磁场相互作用的结果。直接转矩的基本原理是控制ψs恒定,通过调节δ改变电磁转矩。
1.2 传统直接转矩控制系统
传统永磁同步电机的直接转矩控制系统结构如图1所示。定子磁链和转矩观测器用于计算电机的电磁转矩和定子磁链,其输入为电机的定子电压和电流;控制器将定子磁链估计值、转矩估计值、转速估计值、转速给定值以及定子磁链给定值经过滞环比较器输出开关向量,通过开关模式表查询得到三相桥通断信号,进而控制三相桥驱动永磁同步电机。有Ld=Lq,式(1)简化:

图1 传统直接转矩控制框图
图1 中,Udc为电机母线电压,Sa,Sb,Sc为驱动桥开关矢量,ia和ib为电机A,B相电流,为估计的定子磁链幅值,ncmd为期望电机转速,d为定子磁链幅度给定值。将采集的定子A,B相绕组电流经变换后可得到isα,isβ,定子磁链的计算公式如下:
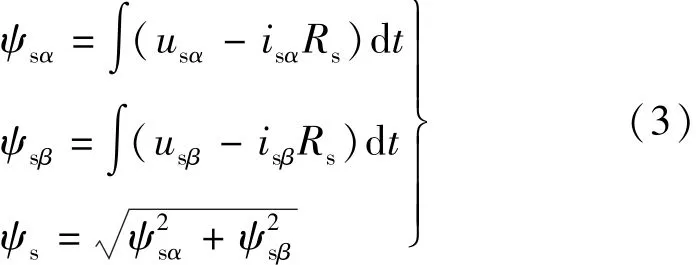
式中:Rs为定子电阻。给定的定子磁链幅值与估计的定子磁链ψs相比得到磁链开关状态。根据ψsα和ψsβ可计算磁链所在的扇区并估计电磁转矩。在定子α-β坐标系下电磁转矩的计算公式如下:

得到 ψsα和 ψsβ后,可计算磁链角度,从而计算电机转速[7]:

为减小高频噪声对微分运算的影响,采用滑动平均滤波方法对式(5)计算得到的速度信号进行滤波处理,基本原理如下:

得到估计的电机转速后,可计算出期望的电磁转矩,与式(4)估计的电磁转矩相比得到转矩开关状态。根据磁链开关状态、转矩开关状态、磁链所在扇区,通过开关表查询得到电机三相驱动桥的开关状态。
传统的直接转矩控制算法需要给定定子磁链参考值,由于厂家提供的电机参数并不准确,并且在运行过程中随着绕组发热电阻增大,电机参数会随之改变,因此恒定的定子参考磁链不能适应电机较宽的工作转速范围,当电机期望转速变化时,恒定的参考磁链会带来较大的转速误差。本文针对参考磁链对电机转速的影响情况进行了仿真,仿真结果如图2和图3所示。仿真用的隐极式永磁同步电机的额定电压为28 V,6对极,电机额定功率为30 W,定子电阻4 Ω,直轴与交轴电感均为2 mH。
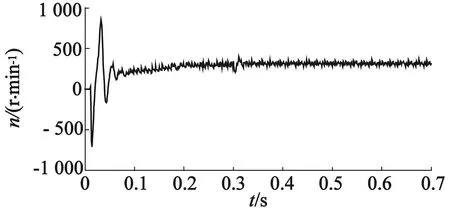
图2 电机转速(给定磁链为0.058 Wb)

图3 电机转速(给定磁链为0.042 Wb)
图2 和图3是对不同定子参考磁链作用下的电机转速仿真,可以看到定子参考磁链分别为0.042 Wb和0.058 Wb时,电机稳态转速相差110 r/min。可见若采用传统的直接转矩控制方案,必须对期望的定子磁链幅值进行校验,这需要通过大量的试验预先获取,并且在实际使用过程中,需要根据电机运行状态实时调整给定磁链幅度,从而影响了直接转矩控制的灵活性。
1.3 基于磁链闭环的直接转矩控制系统
分析式(2),对隐极式电磁转矩表达式,若负载角δ始终为90°,则电磁转矩计算公式如下:

若负载角始终保持最大,则电磁转矩与定子磁链之间存在固定的比例关系,通过控制磁链幅值即可实现转矩的控制,从而控制电机转速。由于磁链通过电流估算得到,而电磁转矩需要通过估算的磁链间接计算,这会引入较大的误差,影响控制效果,因此本文简化了控制结构,去掉了转矩闭环,仅利用磁链幅值控制电机转速,得到基于定子磁链闭环控制的直接转矩控制方案,如图4所示。
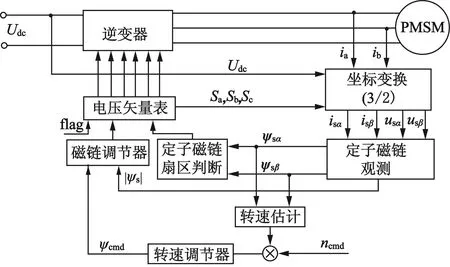
图4 基于磁链控制的直接转矩控制框图
图4 中的flag为控制电机正反转的信号,当flag=1时电机正转,当flag=-1时,电机反转。
2 直接转矩控制方法验证
对基于磁链闭环控制的直接转矩控制方案进行了仿真,图5为仿真电机转速,图6为电机定子磁链ψsα和ψsβ平面图。可以看到当期望转速从400 r/min增加到700 r/min时,电机在0.05 s内实现了转速跟踪。从磁链平面图来看,当电机转速升高时,磁链幅度由0.06 Wb减小到0.04 Wb,在运行过程中,磁链曲线始终保持为圆形。

图5 仿真电机转速

图6 仿真定子磁链
在测功机平台上对基于磁链闭环控制的直接转矩控制方案进行了带载试验,实测电机转速和负载力矩曲线如图7、图8所示。当电机期望转速从400 r/min到300 r/min跃变,同时负载从0到40 mN·m反复跃变,电机仍能较快地跟踪上期望转速,稳态误差在±15 r/min以内,测试结果表明此方案具有较好的动态性能和稳态精度。
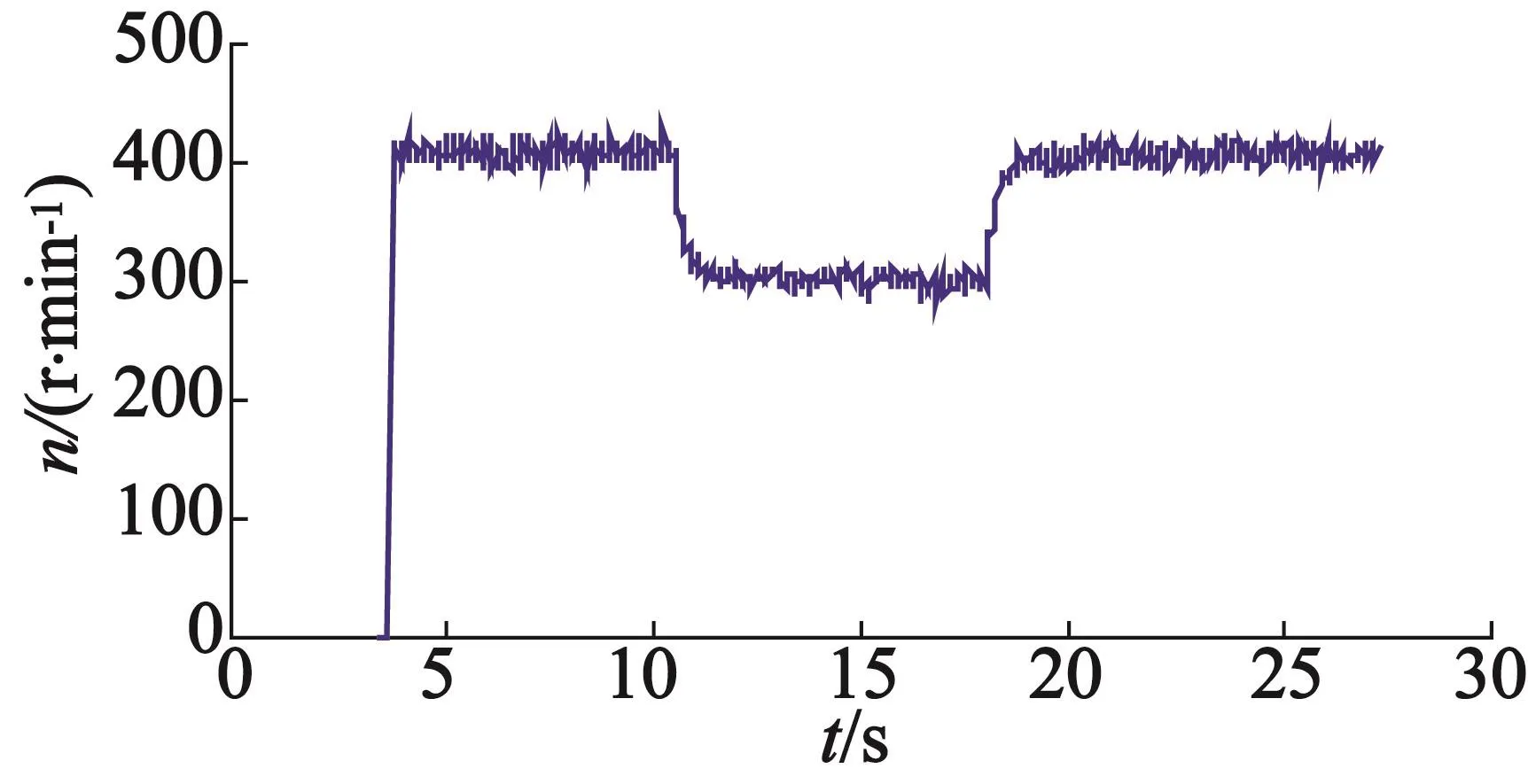
图7 实测电机转速
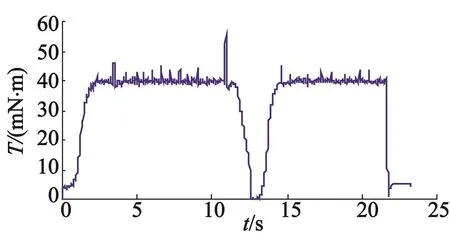
图8 实测负载转矩
3 结 语
本文介绍了一种基于磁链闭环控制的直接转矩控制方案,该方案保留了传统直接转矩控制方案的主要优点,免去了复杂的坐标变换以及电流控制环,同时该方案还取消了对电磁转矩的估计和转矩闭环,实现了控制方案的简化,利于空间环境下的应用。仿真和实验结果表明,该方案相比传统的磁链和转矩双闭环的直接转矩控制算法,减少了计算量,避免了给定磁链幅值不准确对系统性能的影响,同时保留了传统直接转矩控制方案的转矩动态响应的快速性。
参考文献
[1] 刘胜,戚磊.永磁同步电机空间矢量控制方法设计实现[J].控制工程,2009,16(2):247-250.
[2] 何继爱,王惠琴.永磁同步电机空间矢量控制系统的仿真[J].电力系统及其自动化学报,2005,17(6):14-16.
[3] 刘军,楚小刚.基于参考磁链电压空间矢量调制策略的永磁同步电机直接转矩控制研究[J].电工技术学报,2005,20(6):11-15.
[4] 田淳,胡育文.永磁同步电机直接转矩控制系统理论及控制方案的研究[J].电工技术学报,2002,17(1):7-11.
[5] 陶生桂,袁登科.永磁同步电机直接转矩控制系统的改进[J].同济大学学报,2005,33(5):678-682.
[6] 王斌,王跃.基于定子磁链降阶状态观测的永磁同步电机无差拍直接转矩控制系统[J].电工技术学报,2014,29(3):160-171.
[7] 王斌,王跃,王兆安.无速度传感器的永磁同步电机无差拍直接转矩控制方法[J].电机与控制学报,2014,18(6):42-49.
