活性炭固定床吸附苯蒸汽的数值模拟

宋颖韬，党明岩，王鼎雯

(沈阳理工大学 环境与化学工程学院，沈阳 110159)

活性炭固定床吸附苯蒸汽的数值模拟

宋颖韬，党明岩，王鼎雯

(沈阳理工大学 环境与化学工程学院，沈阳 110159)

以守恒定律为基础，结合吸附平衡关系和传质速率方程，建立了活性炭吸附苯蒸汽固定床的数学模型，采用有限差分法对模型方程进行离散，并借助于Matlab软件编程求解，考察了传质系数、进料浓度、空塔气速和温度的变化对吸附过程的影响。计算结果表明，采用本文建立的数学模型可以很好地预测吸附床的负荷变化和穿透曲线，可为吸附床的设计和最优化操作提供理论指导。

活性炭；固定床；吸附；数值模拟

挥发性有机物对环境及人体健康危害极大，目前控制挥发性有机化合物的排放已成为环境保护的热点问题。吸附作为一种挥发性有机物回收技术具有净化效率高、处理量大、能耗低、设备简单等优点，在工业中应用广泛[1-3]。工业上活性炭动态吸附有机化合物的设备主要是固定床，吸附操作时流体流过固定床吸附剂颗粒层，床层中吸附剂的吸附量随着操作过程的进行而逐渐增加，同时床层内各处浓度和温度分布也随时间而变化，相比于一般的固定床反应器，吸附固定床操作的影响因素更加复杂。鉴于动态吸附过程的复杂性和各种参数的耦合性，如果只通过实验方法对其进行研究，既耗时又不经济，而数值模拟是对实验研究的有力补充。国内外对于吸附固定床的研究主要集中在高效吸附剂的开发、吸附性能的实验研究等[4-8]，由于模型的建立及求解的困难，对于固定床吸附器的模拟方面则略显不足。挥发性有机物中比较重要的有苯、甲苯、二甲苯、丙酮等，本文以空气—苯体系为例，采用数值模拟的方法研究活性炭对苯的动态吸附过程，以此为实际吸附过程的操作和设计提供一定的理论依据。

1 吸附固定床数学模型的建立和求解

固定床吸附过程比较复杂，影响因素较多，建立数学模型时首先假设吸附床的轴向气体流速不变，径向速度、压力和浓度分布忽略不计；吸附过程为等温过程；轴向扩散系数为常数。在吸附床轴向上取dz长度的微元体，以其为衡算对象，建立物料衡算方程如下：

(1)

式中：C为气相中苯的浓度，mol/m3；q为吸附量，mol/kg；u为空塔气速，m/s；Dz为轴向扩散系数，m2/s；ρb为床层的堆积密度，kg/m3；ε为床层的空隙率。

目前吸附模拟中使用最为广泛、较为可靠的吸附速率模型是线性动力模型[9]，采用该模型描述吸附速率的方程为

(2)

式中：k为传质系数，s-1；q•为平衡吸附量，mol/kg。

活性炭吸附苯的平衡关系符合Langmuir吸附等温式，即

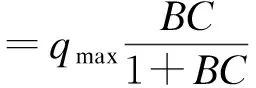
(3)

式中：qmax为最大吸附量，mol/kg；B为Langmuir吸附平衡常数，m3/mol。

根据吸附过程的特征，采用初始条件和边界条件分别为

t=0,C=C0,q=0

(4)

(5)

(6)

由式(1)～(6)组成的微分方程组即为吸附床的数学模型。

由于待求解的模型为偏微分方程组，本文采用有限差分法进行离散。借助于Matlab软件对离散方程进行编程求解。模型参数主要参考文献中提供的实验数据[10]。

2 计算结果和分析

2.1 吸附床层内吸附质浓度变化

在温度T=293.15K、苯进料浓度Cin=0.5mol/m3、床层空隙率ε=0.35、吸附时间t=300min、空塔气速u=0.3m/s、传质系数k=1.5×10-3s-1条件下，模拟计算得到吸附床内苯浓度和吸附量的动态分布规律见图1和图2，图中轴向长度和浓度均采用无量纲数值。由图1和图2可见，随着吸附的进行，在同样的床层位置处苯浓度逐渐增大，相应地吸附量也逐渐增大，而在吸附时间相同时，沿床层长度方向苯浓度和吸附量逐渐减小。从图中可明显看到传质区的形成过程，吸附初始阶段固定床出口附近苯浓度和吸附量均为0，随着传质区向出口方向移动，一段时间后吸附床被穿透，床层出口处苯浓度逐渐增大，直至传质区移出固定床，此时固定床出口处苯浓度接近进料浓度，整个固定床达到吸附饱和，失去吸附能力。以二维图形表示出吸附负荷曲线和透出曲线如图3和图4所示，图3表示出了吸附时间分别为30min、50min和80min时吸附负荷曲线的变化，可明显看到吸附曲线随着时间的变化，当曲线下端到达床层末端时，开始有吸附质的流出。从图4可见，当吸附时间为100min左右时，床层被穿透，此时计算得到床层末端穿透吸附量为0.18mol/kg，此后流出物中苯浓度逐渐增加，到220min时床层出口浓度接近于入口浓度，此时饱和吸附量达到2.86mol/kg。

2.2 传质系数对床层内吸附质浓度分布的影响

为简化计，本文计算中将传质系数k视为常数，而实际生产情况下影响k的因素多而复杂，其数值需要大量的实验数据拟合确定，本文以定性分析为主，仅考察单因素变化的影响。分别取传质系数k为0.8×10-3s-1、1.5×10-3s-1、2.5×10-3s-1，其它参数同2.1，计算得到吸附负荷曲线和透出曲线见图5和图6。从图中可以看出，传质系数越大，传质阻力越小，传质速率越大，吸附越快，故传质区越短，浓度分布曲线越陡。当传质系数较小时，传质区较长，此时若采用的床层较短，则吸附床就会很快被穿透，这样会造成大量的吸附空间不能利用。因此吸附床的操作条件若发生变化，床层高度可能会成为影响吸附效果的因素，这在设计和生产中尤为重要，采用数值模拟的方法可以方便地预测这些影响的结果。模拟计算结果显示，当传质系数从0.8×10-3s-1增加到2.5×10-3s-1时，饱和吸附量由2.88mol/kg变化到2.86mol/kg，说明传质系数的变化对饱和吸附量几乎没有影响。

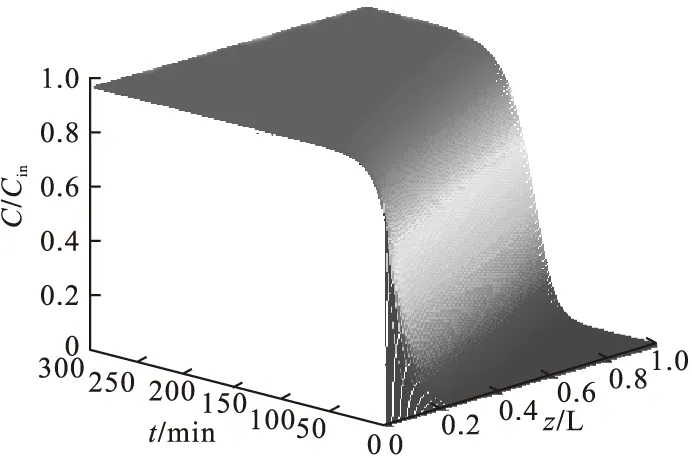
图1 吸附床内气相中苯的浓度分布

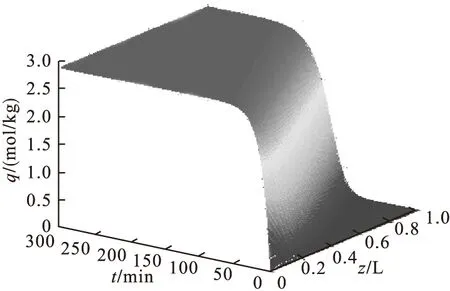
图2 吸附床内固相中苯的吸附量分布

图3 不同时间下的吸附负荷曲线

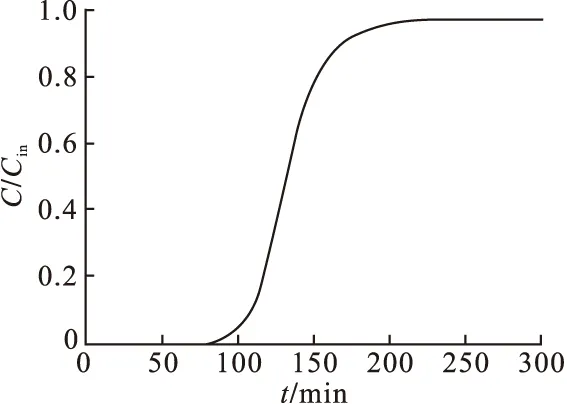
图4 吸附床透出曲线

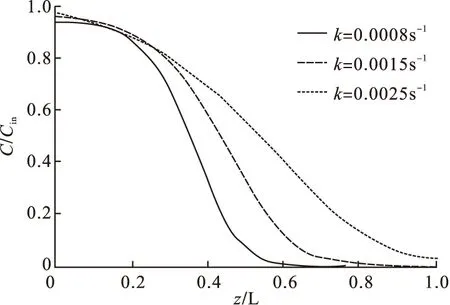
图5 不同传质系数下的吸附负荷曲线(t=60min)

图6 不同传质系数下的透出曲线

2.3 进料浓度对床层内吸附质浓度分布的影响

其它条件同2.1，分别取苯进料浓度Cin=0.35mol/m3、0.5mol/m3、0.65mol/m3，计算得到进料浓度对固定床吸附过程的影响见图7和图8，为更好地表达吸附结果，图8采用以吸附量表示的透出曲线。从图中曲线分布可以看出，进料浓度越高，吸附床相同位置处苯的浓度越大，负荷曲线越靠近右侧。从透出曲线可见，进料浓度越高，穿透时间越短，饱和吸附量越大。这是因为，进料浓度增大，相同时间内进入吸附床的苯量也增大，传递推动力也增加，因此越快达到吸附平衡，使得更多的苯进入下一段床层，从而穿透时间变短。模拟计算结果显示，当进料浓度从0.35mol/m3增加到0.65mol/m3时，饱和吸附量由2.56mol/kg增加到3.07mol/kg。

图7 不同进料浓度下的吸附负荷曲线(t=60min)

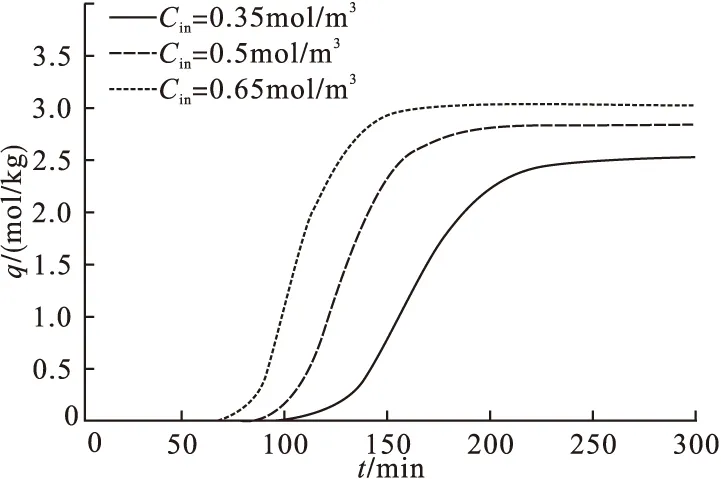
图8 不同进料浓度下的透出曲线

2.4 空塔气速对床层内吸附质浓度分布的影响

其它条件同2.1，分别取空塔气速u为0.2m/s、0.3m/s、0.4m/s，模型计算结果见图9和图10。

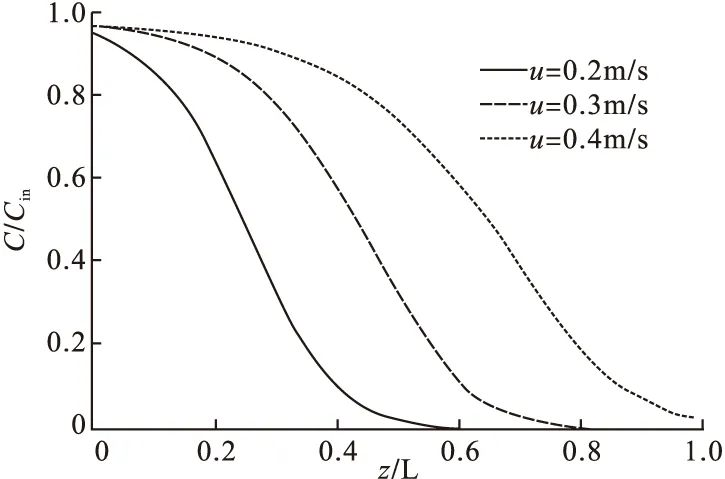
图9 不同空塔气速下的吸附负荷曲线(t=60min)

从图中可以看出，空塔气速对吸附过程影响很大，文中数学模型的左边界采用第三类边界条件，故在入口处苯浓度随空塔气速的不同而不同，空塔气速增加，入口处苯浓度也会有所增加。此外，空塔气速越大，苯浓度分布曲线越平缓，同时由于空塔气速增加，即负荷曲线沿吸附床轴向移动速度加快，同样床层长度下，吸附床越快被穿透。同时由于流速的增大导致气体与吸附剂接触时间减少，苯来不及被吸附就进入下一段床层。从图中还可明显看到，当空塔气速较大时，传质区较长，此时若吸附床较短，也会造成吸附剂利用率低的结果。实际生产中流速加快会使得传质系数也增加，当增加到一定程度时，会造成吸附过程的控制步骤发生变化，使得吸附过程更为复杂。

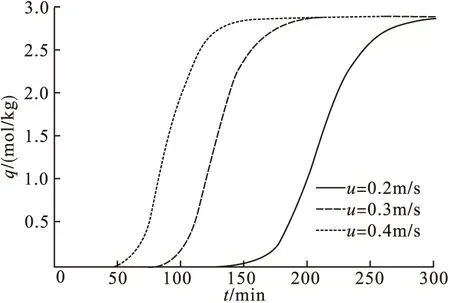
图10 不同空塔气速下的透出曲线

2.5 温度对床层内吸附质浓度分布的影响

其它条件同2.1，在温度T分别取293.15K、303.15K、313.15K时，固定床吸附过程模拟计算结果如图11和图12所示。可以看出，在相同条件下，温度越高时，传质区越长，传质区末端越靠近吸附床出口，床层越快被穿透。从静态吸附分析结果可知活性炭吸附苯是放热过程[10]，随着温度的升高，一方面吸附速率有所增大，另一方面物理吸附过程减弱，两种影响共存下导致传质区位置的不同。因为文中建立数学模型时假设床层内温度不变，不考虑吸附热引起的温度效应，按该数学模型计算时，在一定温度差异范围内，温度对吸附过程影响不是很大，所以浓度曲线总体差异不大。但从透出曲线来看，温度较高时对吸附过程的影响较大，计算结果显示，温度由293K升温至313K时饱和吸附量由2.87mol/kg降低到2.56mol/kg，这与活性炭对苯的吸附为放热过程相符合。

图11 不同温度下的吸附负荷曲线(t=60min)

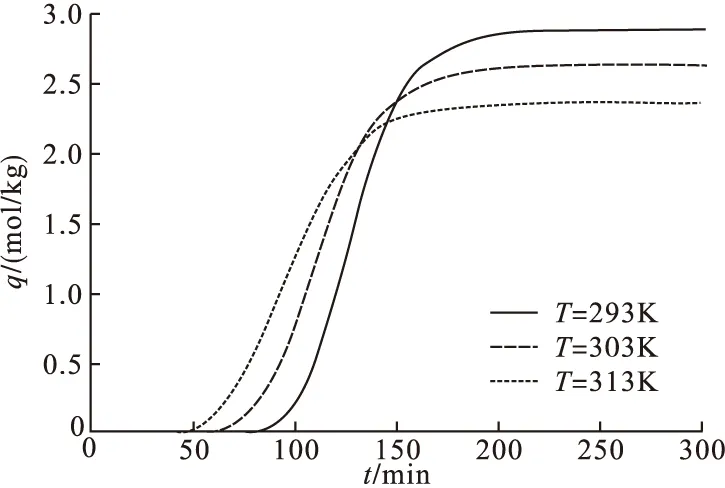
图12 不同温度下的透出曲线

3 结论

(1)通常条件下，随着吸附的进行，同样床层位置处的苯浓度和吸附量都逐渐增大，吸附时间相同时，沿床层轴向苯浓度和吸附量逐渐减小，模拟计算结果显示出传质区的形成和移动过程。

(2)随着传质系数的增大，吸附速率加快，浓度分布曲线变陡，传质区变短，穿透时间增加；随着进料浓度的提高，穿透时间减少，饱和吸附量增加；随着空塔气速的增大，浓度分布曲线变缓，穿透时间减少；随着温度的升高，传质区变长，穿透时间变短，饱和吸附量降低。

(3)所建立的数学模型能够较好地对固定床内的吸附过程进行描述和预测，模拟计算结果比较合理可靠。

[1]陶宇鹏,陈中明,代茂节,等.挥发性有机物(VOCs)污染治理中吸附技术的相关应用[J].低温与特气,2015,33(6):45-50.

[2]陆豪,吴祖良,高翔.吸附法净化挥发性有机物的研究进展[J].环境工程,2013,31(3):93-97.

[3]席劲瑛,武俊良,胡洪营,等.工业VOCs 气体处理技术应用状况调查分析[J].中国环境科学,2012,32(11):1955-1960.

[4]范忠雷,查会平,王玲慧.乙二胺硅胶材料固定床吸附铜离子的研究[J].郑州大学学报,2014,35(1):68-72.

[5]刘娟,王小艺,刘载文.壳聚糖衍生物固定床中Cu(Ⅱ)的吸附性能研究[J].北京工商大学学报:自然科学版,2009,27(2):4-7.

[6]于伟华,刘鹏,龙超,等.疏水性超高交联吸附树脂对氯代烃蒸汽的固定床吸附特性研究[J].环境科学,2011,32(9):2805-2809.

[7]张会平,刘剑,鄢瑛.苯在结构化固定床的吸附动力学[J].化工进展,2011,30(Z):41-45.

[8]苏青青,杨嘉谟.活性炭固定床吸附SO2的机理及动力学研究[J].三峡大学学报:自然科学版,2010,32(5):97-101.

[9]王丹莉,刘向军,刘应书.气体吸附动力学模型的研究现状[J].化工进展,2010,29(Z):5-11.

[10]胡祖美,张艳,王金渠,等.苯在活性炭纤维上吸附等温线的测定及分析[J].石油学报:石油加工,2008,24(4):484-487.

(责任编辑：马金发)

Numerical Simulation of the Benzene Vapor Adsorption onto the Activated Carbon Fixed-bed

SONG Yingtao,DANG Mingyan,WANG Dingwen

(Shenyang Ligong University,Shenyang 110159,China)

The mathematical model for the benzene vapor adsorption onto the activated carbon fixed-bed has been set up on the basis of conservation law along with the adsorption equilibrium relationship and mass transfer velocity equation.The finite differential method was adopted to discrete the equation,while MATLAB programming was also used so as to investigate the effects of mass transfer coefficient,inlet material concentration,superficial gas velocity and the change of temperature on the adsorption process.The calculations show that the mathematical model developed could forecast the load change and the breakthrough curve of the adsorption bed,then provide theoretical guidance to the design and optimization of the adsorption operation.

activated carbon；fixed-bed；adsorption；numerical simulation

2016-03-07

宋颖韬(1972—)，女,副教授,研究方向：化工数值模拟。

1003-1251(2017)02-0088-05

TQ028.1

A