谈谈分离思想在高考题中的应用

☉湖北大学附属中学 蔡有缘

谈谈分离思想在高考题中的应用

☉湖北大学附属中学 蔡有缘

回顾近几年的高考题，无论是地方卷，还是全国卷，分离思想在解决利用导数处理函数与不等式的综合问题，以及求参数的相应题型时，应用比较多.下面就分离思想的应用谈谈自己的看法.

一、利用分离把相同变量放在一边构造函数比较大小

例1（2014年湖北卷22题）π为圆周率，e=2.71828…为自然对数的底数.

（2）求e3，3e，eπ，πe，3π，π3这6个数中的最大数和最小数；

（3）将e3，3e，eπ，πe，3π，π3这6个数按从小到大的顺序排列，并证明你的结论.

易知f（x）在（0，e）上单调递增，在（e，+∞）上单调递减.

所以3lne＞eln3，πln3＞3lnπ，πlne＞elnπ.

所以e3＞3e，3π＞π3，eπ＞πe.

根据函数y=xα（α＞0），y=ex，y=πx在定义域内单调递增，可得3e＜πe＜π3，e3＜eπ＜3π，综上可知3π是最大数，3e是最小数.

（3）略.

利用这种方法我们可以解决下列问题：

附：（1）比较20162017与20172016的大小.

解析：欲比较20162017与20172016的大小，

不妨假设20162017＞20172016，

所以ln20162017＞ln20172016.

所以2017ln2016＞2016ln2017.

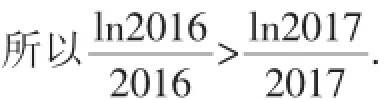
所以f（2016）＞f（2017），

所以20162017＞20172016.

（2）（2001年湖北卷20题的第（2）问）求证（1+m）n＞（1+n）m，其中1≤i≤m＜n，m，n∈N*.

证明：欲证（1+m）n＞（1+n）m，

即证nln（1+m）＞mln（1+n），

由前述知m＜n，

所以f（m）＞f（n），

二、利用分离把不同类型的函数分列不等式的两边，进而比较大小

例2（2014年课标I卷21题）设函数f（x）=aexlnx+，曲线（fx）在点（1，（f1））处的切线方程y=e（x-1）+2.

（1）求a，b；

（2）证明：（fx）＞1.

解析：由条件易知a=1，b=2，在第（2）问中利用分离.

设g（x）=xlnx，则g（′x）=1+lnx.

则h′（x）=e-x（1-x）.

综上，当x＞0时，g（x）＞h（x），即f（x）＞0.

利用这种方法我们可以解决2016年山东卷第20题的第（2）问.

（1）讨论（fx）的单调性；

因为φ（1）=1，φ（2）=-10，所以存在x0∈［1，2］，使得x∈（1，x0）时，φ（x）＞0，x∈（x0，2）时，φ（x）＜0.

所以h（x）在（1，x）0内单调递增，在（x0，2）内单调递减.由h（1）=1，可得，当且仅当x=2时取等号.

三、利用分离求解参数的值或范围

已知x的取值范围利用不等式解决恒成立，存在性问题对所涉及的参数取值问题.

例3（2015年课标I卷12题）设函数f（x）=ex（2x-1）-ax+a，其中a＜1，若存在唯一整数x0，使f（x0）＜0，求a的取值范围.

解析：由f（x0）＜0，即ex0（2x0-1）-a（x0-1）＜0，得ex0（2x0-1）＜a（x0-1）.

当x0=1时，得e＜0，显然不成立.

易知x∈（-∞，0）时，g′（x）＞0，g（x）为增函数；

x∈（0，1）时，g′（x）＜0，g（x）为减函数.

要满足题意，则需x0=0，

此时需满足g（-1）≤a＜g（0），得

例4（2014年辽宁卷11题）已知x∈［-2，1］时，不等式ax3-x2+4x+3≥0恒成立，求实数a的取值范围.

解析：由题意知，∀x∈［-2，1］，都有ax3-x2+4x+3≥0，即ax3≥x2-4x-3在x∈［-2，1］上恒成立.

当x=0时，a∈R.

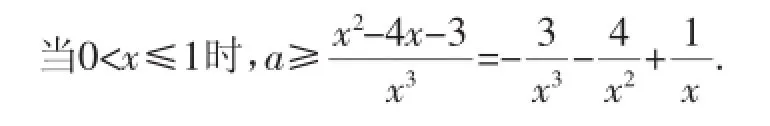
所以g（t）在［1，+∞）上单调递减，g（t）min=g（1）=-6（t≥1），所以a≥-6.

综上，可知-6≤a≤-2.

在利用分离思想求参数的值或范围时，注意讨论参数系数的正负问题.

通过这些高考题的归类和总结，我们不难发现，分离思想在高考中的重要性，因此建议在高三复习中，渗透这种思想应用，让学生熟练掌握.