例谈高考题中对数列不等式放缩的考查

☉湖南省长沙市明德中学 谭隆柯

例谈高考题中对数列不等式放缩的考查

☉湖南省长沙市明德中学 谭隆柯

放缩法是一种常用的证明技巧，主要用于研究与正整数有关的数学问题.猜想与递推是数列中常见的问题.而放缩法时常是数列证明问题中至关重要的一种策略，本文想通过近几年高考试题与各地高考模拟题中，考查数列与不等式所呈现出的方式，探析数列与不等式问题中不等式放缩的几个常用模型.

一、利用几种常见的不等式裂项放缩

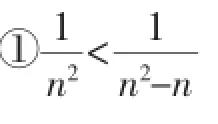
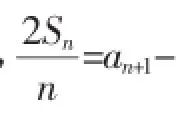
（1）求数列｛an｝的通项公式；

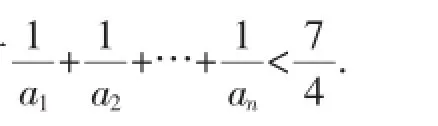
（1）求数列｛an｝的通项公式；

（2）试找整数M，使M＜S31＜M+1.

二、利用对通项公式进行放缩

例3已知数列｛an｝满足a1=1，an+1=3an+1.