全国各省市高考模拟试题中的“亮点”题赏析

☉湖北省襄阳市第一中学 王 勇 王 云

全国各省市高考模拟试题中的“亮点”题赏析

☉湖北省襄阳市第一中学 王 勇 王 云

纵观2017年全国各省市高考数学模拟试题，总体反映出稳定、创新、应用、传承的特点.每份试卷的结构、题型、重要知识点相对稳定，不同试卷均有新颖的“亮点”题，试题注重创设新颖情境，强调知识交汇，突出数学素养和数学灵气的考查.试题设计充分体现数学的应用价值，尤其是与人们的生活、生产紧密联系的实际应用性试题，意在考查考生把实际问题数学模型化的转化思想，而体现数学背景、数学历史、数学文化、数学故事的历史名题的改编题，更是给数学试卷注入了一股春风，彰显了数学文化的传承、数学阅读理解能力的考核.下面精选十三例并分类解析，旨在探索题型规律，揭示解题方法.

一、创设新颖情境，强调知识交汇，突出数学核心素养

高考是选拔性的考试，模拟试卷中出现新颖别致且综合性较强的试题在情理之中.面对情境新颖、交汇整合的题目，需要锁定目标，寻找理论依据，合情推理，逐步套牢目标，不断转化，惊险散尽，自然水到渠成.

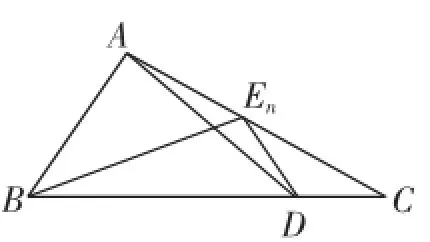
图1

A.3·2n-1-2B.2n-1

C.3n-2D.2·3n-1-1

所以an+1+1=3（an+1），所以｛an+1｝是首项为a1+1=2，公比为3的等比数列.

所以an+1=2·3n-1，所以an=2·3n-1-1.故选D.

点评：本题综合考查向量的运算、向量共线，数列通项公式的求法.此题既有数列又有向量，而且向量还是以一个系列点为起点，应当确定由向量运算剥离出数列递推公式的思路，注意活用共线向量定理.对于构造法求数列的通项公式：形如an+1=pan+q（p≠1，q≠0）的递推关系，可构造一个以p为公比的等比数列｛an+r｝，根据an+1+ r=p（an+r）符合递推关系，可求出

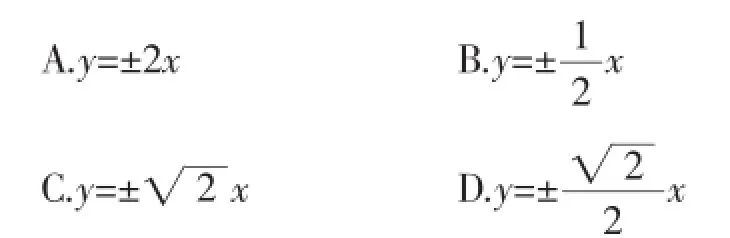
分析：本题要求双曲线的渐近线方程，关键是求出a、b之间的关系.

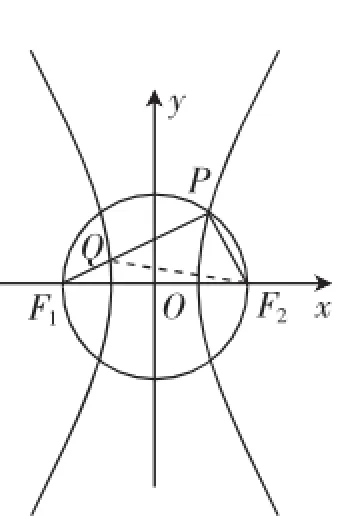
图2

解：如图2，连接QF2.由已知得，|PF1|-|PF2|=2a，|QF2|-|QF1|=2a.设|QF1|=m，则|PQ|=2m.所以|PF1|= 3m，|PF2|=3m-2a，|QF2|=m+2a.因为P是以F1F2为直径的圆与C的交点，所以∠F1PF2=90°，在Rt△QPF2中，有|PQ|2+|PF2|2=|QF2|2，即（2m）2+（3m-2a）2=（m+2a）2，解得所以|PF1|=3m=4a，|PF2|=3m-2a=2a.在Rt△PF1F2中，|PF1|2+ |PF2|2=|F1F2|2，所以（4a）2+（2a）2=（2c）2，即c2=5a2，所以b=

点评：本题先是从双曲线的定义出发得到两个关系式，再根据PQ、QF1的长度关系引入参数m，并在Rt△QPF2中根据勾股定理列式，最后才在焦点△PF1F2中求解a、c的关系.整个解法过程中，算得有方向，算得有思路.本题既有效地关注了学生的运算素养，又十分注重图形性质的运用及数形结合思想的渗透（直观想象核心素养）.

例3（2017年黄冈市质检题）定义在区间（0，+∞）上的函数y=f（x）使不等式2f（x）＜xf′（x）＜3f（x）恒成立，其中f′（x）为f（x）的导函数，则（）.

分析：由题设条件2f（x）＜xf′（x）＜3f（x）可得到两个不等式xf′（x）-3f（x）＜0和xf′（x）-2f（x）＞0，然后利用商函数的导数构造即可.

点评：本题从题设条件看似乎不好下手，其实就是商函数的导数问题，极易与积函数的导数问题混淆，特别是本题需要构造两次商函数才能达到目的.

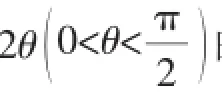
解析：如图3，设圆Q的半径为y，圆P的半径为x，圆P与OA相切于点E，连接PE，则在Rt△POE中以

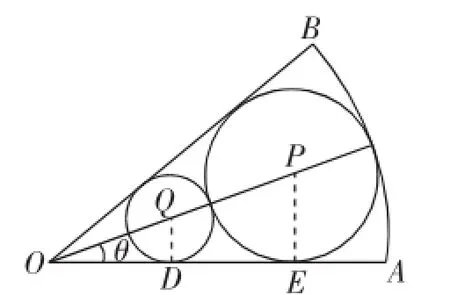
图3

同理，设圆Q与OA相切于点D，连接QD，在Rt△OQD中，可得

点评：本题源于人教A版高中数学必修4第141页的例4，该例设计的是在扇形中内接一个矩形ABCD，探求矩形ABCD面积的最大值，本题改变扇形内接几何图形的形式，在扇形中内接两个相切的圆，探究其中一个圆的面积的最大值.本题涉及的量较多，有θ、x、y和S，求解过程中要理清关系，突出主元，建立目标函数关系式是考查解题能力的最好体现.在处理多个参数问题时，可以通过问题中的辅助条件，结合几何图形消去部分变量，然后化为一个一元函数式，再通过导数进行求解.

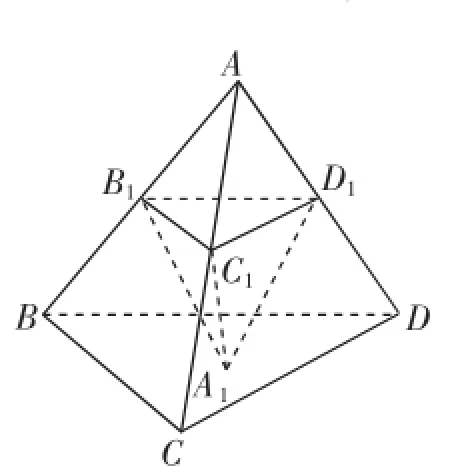
图4

例5（2017年武汉市调考题）如图4，在四面体ABCD中，B1，C1，D1分别在AB，AC，AD上，且平面B1C1D1∥平面BCD，A1为△BCD内一动点，记三棱锥A1-B1C1D1的体积为V.设，则对于函数V=F（x），下列选项正确的是（）.

解析：因为平面B1C1D1∥平面BCD，所以△B1C1D1与△BCD相似.设三棱锥A-BCD的高为h，体积为（tt＞0），三棱锥A1-B1C1D1的高为h1.因为，所以

点评：本题主要考查空间线面位置关系、空间几何体的体积、导数的应用及函数的性质，考查考生的空间想象能力及综合运用所学知识分析问题、解决问题的能力.结合图形，求出V=F（x）的函数解析式是解题的关键.

二、联系生活实际，构建数学模型，注重数学广泛应用

数学是一种工具，工具就有广泛的应用价值，实际应用性问题解答的关键在于选择恰当的数学模型，将实际问题转化为数学问题，“数学化”的过程就是要把陌生问题化为熟悉问题，未知问题化为已知问题，复杂问题化为简单问题.

例6（2017年南昌市模拟题）某物流公司为了配合“北改”项目顺利进行，决定把三环内的租用仓库搬迁到北三环外重新租地建设.已知仓库每月占用费y1与仓库到车站的距离x成反比，而每月车载货物的运费y2与仓库到车站的距离x成正比.据测算，如果在距离车站10千米处建仓库，这两项费用y1，y2分别是2万元和8万元，那么要使这两项费用之和最小，仓库应建在距离车站（）.

A.5千米处B.4千米处

C.3千米处D.2千米处

点评：本题是函数模型和不等式模型的小型综合应用题，利用基本不等式求最值，注意“一正二定三相等”.

图5

例7（2017年武汉市武昌区调考题）如图5，据气象部门预报，在距离某码头南偏东45°方向600km处的热带风暴中心正以20km/h的速度向正北方向移动，距风暴中心450km以内的地区都将受到影响，则该码头将受到热带风暴影响的时间为（）.

A.14hB.15hC.16hD.17h

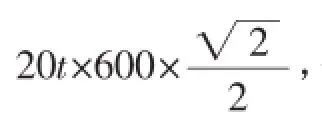
点评：本题是在解三角形的基础上命制的应用题，也是教材中解三角形应用举例在考试中的具体体现，注意2017年高考中对教材上的应用性问题的考查，虽难度不大，但要注意转化和建模.

例8（2017年太原市模拟题）某班同学准备参加学校寒假里组织的“社区服务”“进敬老院”“参观工厂”“民俗调查”“环保宣传”五个项目的社会实践活动，每天只安排一项活动，并要求在周一至周五内完成.其中“参观工厂”与“环保宣传”两项活动必须安排在相邻两天，“民俗调查”活动不能安排在周一.则不同的安排方法的种数是（）.

A.48B.24C.36D.64

解析：当星期一、星期二安排“参观工厂”和“环保宣传”活动时有种，星期三至星期五可以随便安排剩下的活动有种，共有（种）；当星期一不排“参观工厂”或“环保宣传”活动时，从“社区服务”或“进敬老院”中选一项活动来排星期一有种，将“参观工厂”与“环保宣传”两项活动捆绑在一起与剩下的两项活动排在星期二至星期五共有种方法，共有（种），根据分类计数原理知不同的安排方法共有36种.故选C.

点评：本题考查分类、分步计数原理.本题以生活中的实际问题为载体，考查分析问题、解决问题的能力及应用意识；通过计数原理的应用考查运算求解能力.

通过CAE模拟分析，验证不同结构代替现场模具注塑试模。改变了主要依靠经验与直觉，通过反复试模、修模来修正产品设计方案的传统方式，避免了设计的盲目性，同时为模具设计提供价值参考。利用这种方法节省了生产成本，提高了生产效率。结合本次研究，得出如下结论：

例9（2017年北京市西城区模拟题）某赛事组委会要为获奖者制作某工艺品作为奖品，其中一等奖奖品3件，二等奖奖品6件，制作一等奖和二等奖奖品所用原料完全相同，但工艺不同，故价格有所差异，现在甲、乙两家工厂可以制作奖品（一等奖、二等奖奖品均符合要求），甲厂收费便宜，但原料有限，最多只能制作4件奖品，乙厂原料充足，但收费较贵，甲、乙两厂的具体收费情况如下表：

则组委会制作该工艺品的费用总和最低为_________元.

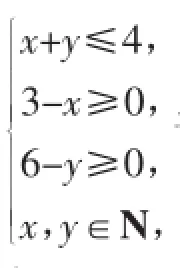
点评：本题考查线性规划的实际应用，考查数学建模思想，分析、解决实际问题的能力及运算求解能力.

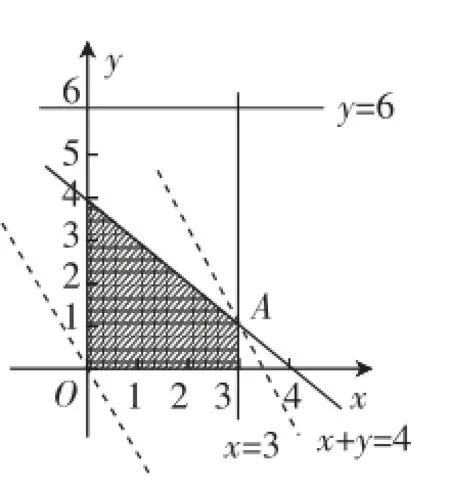
图6

三、依托数学史料，嵌入数学名题，彰显数学厚重文化

数学是一种文化，是一种精神，体现数学文化的新颖试题是近年高考命题的新动向，值得考生关注、探究和学习.教育部考试中心明确要求“在数学中增加数学文化的内容”，预计在2017年的高考中，从《九章算术》和《数书九章》等中国古代数学名著中挖掘素材，考查数学文化的可能性较大.具体的考点有数列、算法、立体几何、推理与证明等相关章节的数学文化题.

例10（2017年河北省三市联考题）我国古代数学著作《九章算术》有如下问题：“今有女子善织，日自倍，五日织五尺，问日织几何？”意思是：“一女子善于织布，每天织的布都是前一天的2倍，已知她5天共织布5尺，问这女子每天分别织多少？”根据上题的已知条件，若要使织布的总尺数不少于30，该女子所需的天数至少为（）.

A.7B.8C.9D.10

点评：我国古代数学涉及等差数列、等比数列的问题很多，因此，涉及等差数列、等比数列的数学文化试题频频出现在各级各类考试卷中.解决这类问题的关键是将古代实际问题转化为现代数学问题，切实掌握等差数列、等比数列的概念、通项公式和前n项和公式是顺利求解的保障.

例11（2017年合肥市模拟题）公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形的面积可无限逼近圆的面积，并创立了“割圆术”，利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14，这就是著名的“徽率”.如图7是利用刘徽的“割圆术”思想设计的一个程序框图，则输出n的值为（）.

图7

A.12B.24C.36D.48

点评：更相减损术、秦九韶算法和割圆术分别在人教A版高中数学必修3第36页，第37页，第45页“算法案例”中出现.其中更相减损术和秦九韶算法分别在2015年和2016年全国卷Ⅱ中考过，因此2017年全国卷考查割圆术的可能性较大.

例12（2017年长沙市模拟题）我国南北朝时期数学家、天文学家——祖暅，提出了著名的祖暅原理：“幂势既同，则积不容异”.“幂”是截面积，“势”是几何体的高，意思是两等高立方体，若在每一等高处的截面积都相等，则两立方体的体积相等.已知某不规则几何体与如图8所对应的几何体满足“幂势同”，则该不规则几何体的体积为（）.

图8

分析：根据题设所给的三视图，想象出图8所对应的几何体是一个正方体挖去一个半圆柱，再根据祖暅原理和有关数据计算即可.

解：由祖暅原理可知，该不规则几何体的体积与已知三视图对应的几何体的体积相等.根据题设所给的三视图，可知其对应的几何体是从一个正方体中挖去一个半圆柱，正方体的体积为23=8，半圆柱的体积12）×2=π，因此该不规则几何体的体积为8-π，故选C.

点评：祖暅原理是我国古代数学家祖暅提出的一个有关几何求积的著名定理，祖暅提出这个原理，要比其他国家的数学家早一千多年.人教A版高中数学必修2第30页“探究与发现”中专门介绍了祖暅原理.本题取材于祖暅原理，考查几何体的三视图和体积计算，既检测了考生的基础知识和基本技能，又展示了中华民族的优秀传统文化.取材于祖暅原理的数学文化题还有很多，例如2013年上海卷第13题，也是利用祖暅原理求有关几何体的体积.

例13（2017年广州市模拟题）如图9的数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角形”.

图9

该表由若干行数字组成，从第二行起，每一行中的数字均等于其“肩上”两数之和，表中最后一行仅有一个数，则这个数为（）.

A.2017×22015B.2017×22014

C.2016×22015D.2016×22014

解析：当第一行有3个数时，最后一行仅有的一个数为8=23-2×（3+1）；

当第一行有4个数时，最后一行仅有的一个数为20= 24-2×（4+1）；

当第一行有5个数时，最后一行仅有的一个数为48= 25-2×（5+1）；

当第一行有6个数时，最后一行仅有的一个数为112=26-2×（6+1）；

……

归纳推理可得，当第一行有2016个数时，最后一行仅有的一个数为22016-2×（2016+1）=2017×22014.故选B.

点评：杨辉三角是人教A版高中数学选修2-3第35页“探究与发现”中提到的中国古代数学的优秀成果.利用杨辉三角的性质，可以把这一古代优秀成果发展应用于很多现代数学分支，例如，利用杨辉三角可以发现高阶等差数列的计算规律，推导高次方程的计算方法，解释无穷级数的概念等.因此虽然高考曾经多次考查过杨辉三角，但2017年全国卷考查杨辉三角的可能性仍然较大.F