一种无损伤的图像加密算法及其实现

吕 翔， 杨刘洋, , 刘中帅

(1.浙江师范大学 数理与信息工程学院，浙江 金华 321004；2.重庆市潼南中学，重庆 402660)

一种无损伤的图像加密算法及其实现

吕 翔1， 杨刘洋1, 2, 刘中帅2

(1.浙江师范大学 数理与信息工程学院，浙江 金华 321004；2.重庆市潼南中学，重庆 402660)

针对一些图像加密算法计算量大、安全性低、密钥数量大和图像部分信息丢失等缺点,提出了一种无损伤的图像加密算法.先将目标图像与拉丁方按位进行异或运算可得初始加密图像,以实现第1步像素值变换加密处理,可减小计算量,并初步提高安全性.再对初始加密图像按照循环自正交拉丁方的数对方阵规律进行第2步像素空间位置变换加密处理,可得最终加密图像,使得图像的安全性更高.仿真实验及结果分析表明:该算法不仅具有安全性高,加/解密效果理想,便于实现等优点,还能抵抗多种攻击,是一种安全实用的无损伤图像加密算法,在高精度图像加密中具有更加广阔的应用前景.

图像处理；信息隐藏；拉丁方；循环自正交拉丁方；仿真实验

0 引 言

为满足社会对信息量不断增加的需求及应对各种信息网络的发展,人们设计了多种具有一定安全性的传输技术、传输设备，同时也发展了相应的保护技术,使得信息传输的速度、质量和安全性都得到了一定程度的保证.但总会有一些技术、设备仍然存在一定的漏洞或缺点,给一些不法分子有机可乘,他们利用这些漏洞或缺点对信息进行截取、篡改、伪装、干扰等多种攻击,以便获取或者破坏一些重要信息.为了提高信息在传输过程中的安全性,人们设计了多种信息隐藏和保护技术.由于图像信息的数据量大,其安全性也就更受人们的关注,为此,学界提出了一系列的图像保护方案和加密方案.

在图像的版权保护方面,数字水印技术[1- 5]扮演着重要的角色,它使得人们可以更加方便、准确地区别正版与盗版.但在需要完全隐藏图像信息的时候,数字水印技术就不再适用了,迫使人们设计出安全性更高的图像加密方案,比如文献[6- 19]等.图像加密通常是在传输或者保存之前完成,按照一定步骤和方法对目标图像进行不同规则的加密操作,使目标图像变为人和机器都无法直接识别、杂乱无章的加密图像.即使在传输过程中或者保存时发生泄漏或者剽取,在不知道加密算法和密钥的前提下也是无法正确获取其中的重要信息,从而大大提高了图像的安全性.

由于最近十年来,组合数学、代数数论、密码学和信息理论得到了蓬勃发展,使得一些基于组合数学和数论等数学方法的加密方案不断被提出来,比如文献[6- 22]等.目前,对以拉丁方为基础的图像加密方案研究还比较少,也不够系统.比如,2001年,李国富等[10]提出以素数幂阶正交拉丁方组为基础,采用有限域方法构造正交拉丁方,对目标图像的像素坐标进行空间位置变换加密.该方案得到的加密图像不但安全性不够高,缺少相关分析,而且所使用的正交拉丁方组的构造也要受到素数幂阶的限制.到2008年,巨亚荣等[11]共同提出将Logistic混沌序列和正交拉丁方相结合用于图像加密.虽然其加密图像的安全性得到了一定程度的提高,但用混沌序列加密时其计算量较大,且同样存在其应用受素数幂阶限制的问题.以上2种加密方案都缺少对加密效果、参数及安全性进行一定量的分析.2015年,杨刘洋等[12]提出了一种以完备拉丁方为基础的像素值和像素坐标双重变换的图像加密算法,不仅提高了加密图像的安全性,而且完备拉丁方的构造也不受素数幂阶的限制,使得应用范围也更加广泛.

为了寻求更加简单有效的加密方案,本文提出了一种以循环自正交拉丁方为基础的无损伤图像加密算法,并通过仿真来实现加/解密操作.该算法属于一种无损伤的加密算法.通过加/解密、抗攻击实验仿真和图像参数计算分析可以看出,加/解密效果理想,安全性高,可以抵抗多种攻击,也表明本文提出的图像加密方法比文献[10- 12]等报道的方法更加实用和有效.

1 无损伤的图像加密算法设计

1.1 循环自正交拉丁方的构造

定义1[12]若由n元集Sn={0,1,2,…,n-1}中各元素构成一个大小为n×n的方阵A(n)=(aij) (aij,i,j∈Sn),并且使得方阵的每行、每列中各元素aij当且仅当出现一次,则称方阵A(n)为一个n阶拉丁方.

定义2 如果2个n阶拉丁方A(n)=(aij)和B(n)=(bij)的并置矩阵C(n)=(aij,bij) (i,j∈Sn)中各元素数对互异,那么称拉丁方A(n)和B(n)为一对n阶相互正交拉丁方,记为A(n)⊥B(n).

定义3 如果一个n阶拉丁方A(n)=(aij)与其转置拉丁方A(n)T=(aji)满足：A(n)⊥A(n)T,那么称拉丁方A(n)为一个n阶自正交拉丁方(Self- Orthogonal Latin Square),记为SOLS(n).

定义4[23]设A(n)为加法群Sn上的一个SOLS (n),若对任意aij,i,j∈Sn,都有

则称A(n)为一个n阶循环自正交拉丁方(Cyclic Self- Orthogonal Latin Square),记为CSOLS(n).

引理1[23]设n为正整数,则SOLS(n)存在的充分必要条件为n∉{2,3,6}.

引理2[23]若n为奇数,且(n,6)=1,则存在CSOLS(n);若设A(n)=(aij),则有aij≡2i-j(modn),(i,j∈Sn).

引理3[24]若设n阶各种类型拉丁方的总数为L(n),则有L(n)≥(n!)2n/(nn)n.

由引理1和引理2可知,只有大于3的奇数阶才存在CSOLS(n),偶数阶则不存在CSOLS(n).例如：根据定义4和引理2构造的A(5)即为CSOLS(5),如下所示:

1.2 基于任何类型拉丁方的像素值变换加密

图像的像素值范围一般都为[0,255],结合目标图像的大小,分2种情况进行加密.若设加密前的目标图像O(n)为n×n的256级灰度图,则有：

1)若n≤256,则可随意选择一种类型的n阶拉丁方A(n).然后将目标图像O(n)与A(n)按位进行异或运算实现第1步像素值变换加密,其加密图像为M(n).

2)若n>256,则先随意选择一种类型n阶拉丁方A(n),然后对A(n)中元素(aij≥256)进行连续取模运算直到所有元素aij≤256为止,得到一个矩阵B(n),如式(2)所示.再将目标图像O(n)与B(n)按位进行异或运算实现第1步像素值变换加密,其加密图像为M(n).

B(n)=A(n) (mod 256).

由引理3可知,任何类型拉丁方的总数量会随着阶数的增长而变得非常巨大.因此,基于以上的拉丁方像素值变换加密时,其密钥空间会非常巨大,如果他人想通过穷举途径解密,几乎不可能,从而也提高了加密图像的安全性.

1.3 基于循环自正交拉丁方的像素空间位置变换加密

如果要对目标图像M(n)的像素空间位置进行变换加密,就需要提供一个与其等大的空间位置变换矩阵K(n),使得K(n)能够满足“变换前后像素的空间位置具有一一映射”关系.由于循环自正交拉丁方A(n)与其转置拉丁方A(n)T的并置矩阵C(n)=(aij,aji) (i,j∈Sn)中的有序元素数对恰好具备该性质,因此,可将C(n)作为空间位置变换矩阵.相对正交拉丁方而言,不但循环自正交拉丁方的阶数不受素数幂限制,而且拉丁方数量也减少了1/2.同理,可结合目标图像M(n)的大小,分2种情况进行加密.

1)若n为奇数,则可先根据引理2构造一个CSOLS(n),设为P(n),然后令P(n)与P(n)T的并置矩阵C(n)=(aij,aji) (i,j∈Sn)中元素aii=i+1(modn),即得由n2个不同有序元素数对组成的空间位置变换矩阵K(n).如果将K(n)中的有序元素数对作为M(n)的新坐标,按照K(n)的规律对M(n)进行一定次数的坐标替换，就可实现第2步像素空间位置变换加密,其加密图像为E(n).例如：

2)若n为偶数,则可先根据引理2构造一个CSOLS(n-1),设为P(n-1),然后对P(n-1)与P(n-1)T的并置矩阵C(n-1)= (aij,aji) (i,j∈Sn-1)补充最后一列为(n-1,i)(i∈Sn)和最后一行为(i,n-1)(i∈Sn),可得一个新数对矩阵D(n)= (aij,aji) (i,j∈Sn),最后令D(n)中的元素aii=i+1(modn),即得由n2个不同有序元素数对组成的空间位置变换矩阵K(n).如果将K(n)中的元素数对作为M(n)的新坐标,结合K(n)的规律对M(n)进行一定次数的坐标替换,就可实现第2步像素空间位置变换加密,其加密图像为E(n).例如：

1.4 具有双重变换的无损伤加/解密算法设计

本文将拉丁方的总数量随着阶数急剧增长和循环自正交拉丁方的独特构造方法及独特结构等优势相结合，提出了将像素值变换与像素空间位置变换相结合的双重变换加密算法.通过该算法不但可以得到理想的加/解密效果,而且图像的安全性得到提高,图像的信息也没有任何缺失.其加/解密的算法流程如图1所示,详细的加密算法步骤如下所述,而解密只需进行逆操作.

图1 加/解密算法流程图

1)输入一个目标图像O(n);

2)判断O(n)的大小,得到n;

3)依据n选择一个拉丁方A(n)或者矩阵B(n),并将A(n)作为密钥1;

4)将O(n)与A(n)或者矩阵B(n)按位进行异或运算,获得第1步加密图像M(n);

5)由n和引理2构造一个CSOLS(n),记为P(n),或者CSOLS(n-1),记为P(n-1),并将P(n)或者P(n-1)作为密钥2;

6)将P(n)或者P(n-1)转换成空间位置变换矩阵K(n);

7)将K(n)中的有序元素数对作为M(n)的新坐标,并按照K(n)的规律对M(n)进行x(x≥1)次坐标位置替换,并将x作为密钥3,即可获得第2步加密图像E(n);

8)判断加密任务是否完成,如果完成就直接输出E(n),否则继续进行.

2 算法实现：仿真实验及结果分析

依据图1中已知的加/解密算法,在个人PC机上通过同时具有计算和仿真两大功能的软件MATL- AB 7.11对251×251的目标灰度图camerman.bmp进行一系列的加/解密仿真实验和参数计算.由于密钥1即A(n)的类型可以随意选取,因此,也可由引理2来构造A(n).在下面的仿真实验中,采用的密钥A(251)就是一个CSOLS(251).

2.1 像素值变换加密及其统计特性分析

通过以上加密算法对目标图进行了加密仿真操作和加密前后图像的像素值分布规律统计,如图2和图3所示.

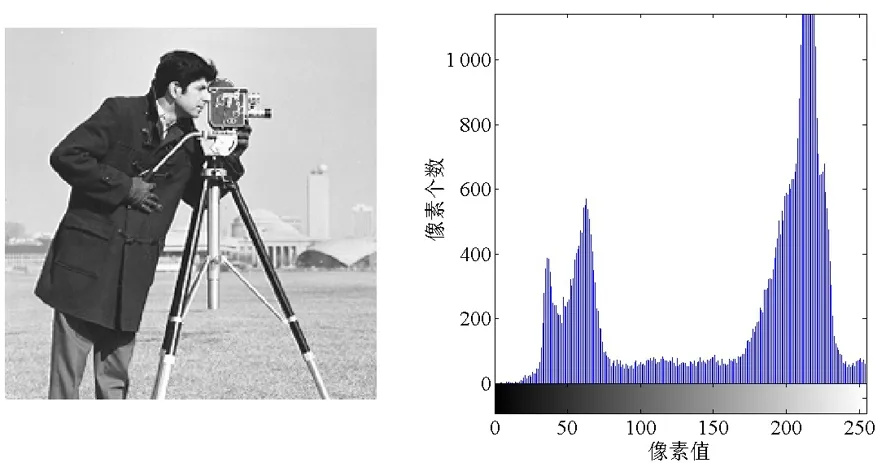
(a)目标图 (b)目标直方图

图2 目标图及其直方图

(a)加密图 (b)加密直方图

图3 加密图及其直方图

从图2和图3可以看出,像素值变换加密前后直方图发生了明显变化,加密图像和目标图像的统计特性完全不同.这说明该加密算法使得图像中的各种像素分布得更加均匀,极大地降低了各像素之间、两图之间的相关性,可抵抗统计分析的攻击.

2.2 像素空间位置变换加/解密及其结果分析

在第2步加密实验中,如果以图3(a)作为像素空间位置变换加密的目标图,则经过本次加密后可以得到如图4所示的通过不同变换次数(x取不同的值)的效果图.

从图3和图4可以看出,基于循环自正交拉丁方的像素空间位置变换会使加密图像更像随机噪声,将原图像中的信息隐藏得更好.当x≥10次时,其加密效果就已经非常理想了,无法识别出原图像中包含的各种重要信息.由此还可以看出,采用双重加密可以更大幅度地提高图像的安全性.

(a)x=1加密图

(b)x=5加密图

(c)x=10加密图

(d)x=50加密图

(e)x=100加密图

(f)x=200加密图

图4 具有不同变换次数的加密图

从图1可看出,解/加密互为逆操作.如果以图4中的图(f)作为解密目标图,并用正确的密钥[P(251),x=200]进行解密操作,则可得到其正确的解密图,如图5(b)所示.但如果使用错误的密钥[P(251),x=198]进行解密操作,就会得到错误的解密图像,如图5(c)所示.如果直接一次使用全部正确的密钥[A(251),P(251),x=200]进行解密操作,就可得到正确的双重解密图像,如图5(d)所示.通过解密图与目标图的对比,发现两者完全相同,因此可以判断：该加密算法属于一种无损伤的图像加密算法,并且对密钥的依赖性很强.

从图3、图4及图5可以看出,不但加密效果理想,而且解密效果也非常好.不仅从视觉效果上看，目标图像的信息得到了很好的隐藏,而且图像的统计特性也非常好.从这些图像效果可以看出,该加密算法具有操作简单、安全、有效等优点.

(a)解密目标图

(b)正确[P(251),x=200]解密图

(c) 错误[P(251),x=198]

(d) 正确[A(251),P(251),解密图x=200]解密图

图5 正确和错误密钥解密图

2.3 加密图像的参数计算及其结果分析

目前,关于图像加密算法的性能评定方法已经出现多种[25- 28].综合考虑各种评定的优劣势,本文将主要根据文献[25- 26]中所给出的4个方面的评价参数“不动点比”“信息熵”“灰度平均变化值”及“相似度”进行相关的计算和分析.与这4个评价参数相关的定义和计算公式则可参照文献[25- 26].如果设目标图像为O(251),经过第1步像素值变换加密后的图像为M(251),经过第2步(x=100次)像素空间位置变换加密后的图像为E(251),则经过计算后可得这三者的详细参数,具体见表1～表4.

2.3.1 不动点比

目标图像与加密图像的不动点比如表1所示.与图像O(251)相比,M(251)和E(251)的不动点比不但下降明显,而且比值还极低.从统计学角度看,不动点比能够从数量上直观地反映出图像M(251),E(251)与O(251)之间的像素变化情况.表1数据反映的情况与图2～图4都相符,这说明了本文提出的加密算法不仅有效,而且效果理想.

表1 目标图与加密图的不动点比

2.3.2 信息熵

从表2可以看出,图像M(251)和E(251)的信息熵比O(251)更加接近256级像素值图像信息熵的最大值8.将表2数据与图2～图4相结合,更能说明加密后的图像像素值分布相当均匀.这也大大降低了攻击者通过像素值统计分析进行成功解密的可能性.

表2 目标图与加密图的信息熵

2.3.3 灰度平均变化值

由表3可知,图像M(251)和E(251)的灰度平均变化值明显比O(251)的更大,这说明该加密算法可以较大幅度地改变图像的灰度平均变化值.由于E(251)比M(251)的灰度平均变化值更高,说明使用双重变换加密效果会更加理想.

表3 目标图与加密图的灰度平均变化值

2.3.4 相似度

从表4可以看出,图像M(251)和E(251)相对于O(251)而言相似度都有比较明显的差别,而且E(251)比M(251)的相似度更低.这说明该加密图像安全性好,能够达到较好的加密目的.如果用其他图像进行加密,也可以得到类似的结果.

表4 目标图与加密图的相似度

如果将表1～表3与文献[12]中表2～表4(在相同参数x=100的前提下)进行对比,就可看出,本文所得不动点比更低,信息熵更高,灰度平均变化值也更高.从这些数据也能说明本文提出的加密算法得到的加密效果更加理想,参数性能更优.

2.4 抗攻击实验及其结果分析

为了更加深入地研究本文提出的图像加密算法的有效性和安全性,笔者进行了一定量的抗攻击仿真实验.比如剪切攻击、椒盐噪声攻击、JPEG压缩攻击、Gaussian低通滤波攻击等仿真实验,其解密效果如图6～图11所示，其中:图6～图8为抗剪切攻击及解密恢复图；图9～图11为抗其他攻击及解密恢复图.

(a)x=100加密图 (b)1/4剪切图 (c)解密效果图

图6 经[A(251),P(251),x=100]加密后的 抗1/4剪切攻击及解密恢复图

(a)x=100加密图 (b)1/2剪切图 (c)解密效果图

图7 经[A(251),P(251),x=100]加密后的 抗1/2剪切攻击及解密恢复图

(a)x=100加密图 (b)3/4剪切图 (c)解密恢复效果图

图8 经[A(251),P(251),x=100]加密后的 抗3/4剪切攻击及解密恢复图

(a)x=100加密图 (b)加椒盐噪声图 (c)解密恢复效果图

图9 经[A(251),P(251),x=100]加密后的 抗椒盐噪声攻击及解密恢复图

(a)x=100加密图 (b)JPEG压缩图 (c)解密恢复效果图

图10 经[A(251),P(251),x=100]加密后的 抗JPEG压缩攻击及解密恢复图

(a)x=100加密图 (b) Gaussian低通 (c) 解密恢复滤波图效果图

图11 经[A(251),P(251),x=100]加密后的 抗Gaussian低通滤波攻击及解密恢复图

从以上几次抗剪切攻击实验结果可以看出,即使加密图像被剪切的信息很多,剩余的信息较少,仍能够恢复出原来目标图像的基本信息,这足以说明本文的加密算法对剪切操作具有很好的抗攻击能力,其稳健性良好.

从抗椒盐噪声攻击、抗JPEG压缩攻击和抗Gaussian低通滤波攻击实验结果可以看出,使用本文加密算法后的加密图像,在受到多种攻击时,不仅能够恢复出包含原来目标图像基本信息的解密图,而且效果还比较好.此外,由于拉丁方的总数量会随着阶数的增长而急剧增长, 11阶就已超过1050个,阶数再升高总数就大得惊人,这就提供了一个庞大的密钥空间,因此,本加密方法对于穷举攻击有很强的抵抗性.同时,基于拉丁方的像素值变换加密可以有效地降低像素值的局部分布,让所有的像素都基本上分布均匀(如图3所示),大幅度地降低了像素之间的相关性,故可以有效抵抗统计攻击.综上,在密钥保管安全的前提下,该加密算法具备很好的抗攻击能力.

3 结 论

从近几十年看,图像加密技术已倍受人们的关注.已知的主要方法大多集中在各种数学方法、物理学方法及两者相结合的加密方法.然而各种基于数学方法的图像加密算法如雨后春笋,不断涌现.即使各有优点,但也不免有其缺点,比如计算量大、加密算法复杂、加/解密效果不够理想、安全性分析不足、对图像有损伤、不能抵抗攻击、应用范围太小等.而本文中提出的一种以循环自正交拉丁方为基础的无损伤图像加密算法,同混沌序列生成和正交拉丁方构造相比,循环自正交拉丁方的构造方法更加简单、且加密时的计算量更少.与完备拉丁方性质相似,只需要用一个拉丁方就可得到与正交拉丁方一样的规律,不仅可以减少拉丁方使用的数量,而且其阶数还不受素数幂的限制,对于所有阶数也都适用,说明其适用性比文献[10- 12]更加广泛.同超混沌系统图像加密[17,19]方法相比,拉丁方的数学模型、计算步骤都更加简单、快捷(可以直接用于加密),不需要多个复杂的微分方程和多步处理.由于超混沌系统计算模式固定,而不同类型的拉丁方构造方法不同,即使同类型也有不同构造方法,因此,拉丁方的构造模式更灵活.由于该加密算法不仅对图像没有一点损伤,加/解密效果理想,而且还可以抵抗多种攻击,因此,本文的加密算法可在高精度图像加密领域中发挥重要作用.

[1]Yen E,Lin L H.Rubik′s cube water mark technology for grayscale images[J].Expert Systems with Applications,2010,37(6):4033- 4039.

[2]黄娜,侯刚,王国祥,等.基于图像内容敏感度分析数字水印算法[J].计算机应用研究,2010,27(5):1898- 1901.

[3]贺冲,王慧琴.DWT域基于系数量化的盲水印算法[J].通信技术,2010,43(3):159- 164.

[4]Merrim S.An image watermarking algorithm based on chaotic maps and wavelet transform[J].International ISC Conference on Information Security and Cryptology,2012,97(2):135- 140.

[5]徐光宪,李玉华,张鑫.基于幻方变换的抗剪切扩频水印算法研究[J].清华大学学报:自然科学版,2013,53(8):1087- 1090.

[6]Mishra M,Mishra P.Image encryption using Fibonacci- Lucas transformation[J].International Journal on Cryptography and Information Security,2012,2(3):131- 141.

[7]王冬梅,黄琳,王金荣.幻方变换加密数字全息图[J].浙江工业大学学报,2007,35(1):116- 118.

[8]袁岁维,范九伦.一种基于排序变换的图像加密算法[J].西安邮电学院学报,2010,15(3):60- 67.

[9]Acharya B,Panigrahy S K,Patra S K,et al.Image encryption using advanced Hill cipher algorithm[J].International Journal of Recent Trends in Engineering,2009,1(1):663- 667.

[10]李国富.基于正交拉丁方的数字图像置乱方法[J].北方工业大学学报,2001,13(1):14- 16.

[11]巨亚荣,刘小兵.一种基于Logistic模型和正交拉丁方变换的图像加密方法[J].重庆科技学院学报:自然科学版,2008,8(10):143- 146.

[12]杨刘洋,吕翔.一种基于完备拉丁方的图像加密算法[J].计算机应用研究,2015,32(11):3433- 3442.

[13]孙烨华,章仁江.计算Arnold变换周期的新算法[J].计算机技术与发展,2008,18(11):66- 68.

[14]彭成,柳林.基于混沌序列的压缩图像加密算法[J].计算机工程,2008,34(20):177- 179.

[15]Wang K,Pei W J,Zou L H.On the security of 3D cat map based symmetric image encryption scheme[J].Physics Letters A,2005,343(6):432- 439.

[16]刘钺.一种小波变换域图像加密技术[J].计算机应用,2010,46(19):157- 159.

[17]黄波,张林华,段婉玉.一种基于Henon映射的图像加密算法[J].重庆工商大学学报:自然科学版,2013,30(11):62- 65.

[18]吕善翔,王兆山,盛堰,等.一种保持非负整数的图像加密算法[J].光子学报,2012,41(11):1365- 1371.

[19]陈在平,蔡鹏飞,董恩增.基于超混沌AES图像加密算法[J].吉林大学学报:信息科学版,2013,31(2):158- 164.

[20]王银花,柴晓冬,周成鹏,等.基于分数傅里叶变换的混沌图像加密方法[J].计算机工程,2007,33(12):172- 174.

[21]孙玉峰,陈建华.一种基于万有引力模型的图像置乱新方法[J].福州大学学报:自然科学版,2006,34(1):47- 50.

[22]花丽丽.基于数字相移全息及图像置乱的光学混沌加密算法研究[D].南京:南京邮电大学,2014.

[23]沈灏.组合设计理论[M].2版.上海:上海交通大学出版社,2008:184- 190.

[24]Vant L J H,Wilson R M.组合数学教程[M].刘振宏,赵振江,译.2版.北京:机械工业出版社,2007:114- 115.

[25]徐江峰,杨有.加密图像置乱性能分析[J].计算机科学,2006,3(33):110- 113.

[26]王迤冉,王春霞,詹新生.一种图像加密算法的性能评价方法[J].微计算机信息,2006,22(30):313- 314.

[27]黄建,柏森.一种有效的图像置乱程度衡量方法[J].计算机工程与应用,2009,45(30):200- 203.

[28]卢振泰,黎罗罗.一种新的衡量图像置乱程度的方法[J].中山大学学报:自然科学版,2005,44(6):126- 129.

(责任编辑 杜利民)

A lossless image encryption algorithm and its implementation

LÜ Xiang1, YANG Liuyang1,2, LIU Zhongshuai2

(1.CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China; 2.TongnanMiddleSchool,Chongqing402660,China)

According to the disadvantages of some image encryption algorithm such as long computation time consumption, low security performance and large number of secret keys requirement and partial information loss, a novel lossless image encryption algorithm was proposed. Firstly, XOR operation was carried out between a selected Latin square and the target image to get the encrypted image. Secondly, scrambling encryption was performed for this image by using a number pair matrix which was generated by a cyclic self- orthogonal Latin square for improving the security. Simulation results and parameter analysis indicated that this algorithm had advantages of high security, attractive performance at encryption/decryption, easy to implement and high resistance of many kinds of attack. Thus, this algorithm was an effective lossless encryption algorithm and had wide application in high precision image encryption.

image processing; information hiding; Latin square; cyclic self- orthogonal Latin square; simulation experiment

10.16218/j.issn.1001- 5051.2017.02.006

2016- 12- 13；

2016- 12- 30

浙江省科技厅创新团队项目(2010R5007)

吕 翔(1979-),男,浙江金华人,副教授,博士.研究方向:通信系统；通信编码理论；组合数学.

TP309.7

A

1001- 5051(2017)02- 0153- 08