基于逻辑公式的粒类互逆运算研究

靳瑞霞，朱云峰，杜新欣

（新乡医学院三全学院，新乡 453000）

基于逻辑公式的粒类互逆运算研究

靳瑞霞，朱云峰，杜新欣

（新乡医学院三全学院，新乡 453000）

粒计算被公认为一种看待客观世界的方法论，是一种问题求解的计算思维方式和策略。基于此，以逻辑语义建立的粒类运算为基础，定义并说明抽象粒中的粒类运算是一对互逆运算，并利用信息系统中的等价关系和分明关系进行实例分析和说明，得出针对互补关系应用不同运算可以得到相同结果的结论。即对同一问题的解决，可以根据不同的条件，采用更合适的方式达到最优解决方法。

抽象粒；粒类运算；互逆关系；互补关系

0 引言

自1997年T.Y.Lin引入粒计算这个概念后，针对粒计算的研究成果层出不穷。虽然不同研究者在各自领域对粒计算进行了不同的定义和扩展，但对于粒计算的直观意义则具有共识，都认为粒计算的内涵包含两个方面：首先是粒本身的直观认识，即粒是以某种方式从整体中分离出的部分；其次是粒计算的直观认识，即把粒看作整体的部分时，粒间的关系、粒与整体的联系、粒间的组合、转换、推理，粒自身的性质等都可以认为是直观意义下的粒计算。目前，粒计算被公认为一种看待客观世界的方法论，在经历了不同的专家学者各个领域的多种思想、模型、方法和技术的研究后，粒计算成为一种问题求解的计算思维方式和策略。

从粒计算是一种思维方式的角度出发，不涉及任何特定领域的粒定义，单纯从数学角度应用形式化的语言来描述，这是基于逻辑公式的形式化粒计算研究的方向，同时也是对粒计算理论体系的有益补充和完善。

本文对基于逻辑公式的粒计算系统进行了扩充，说明在粒类运算上建立的特定粒层对于某些同等类型的互补关系运算具有不变性，并列举实例进行简要验证，从而使得同等性质的粒类关系运算更为灵活，并具有内部关系不变性的特点。

1 抽象粒及粒类运算定义

基于逻辑公式的抽象粒建立在公式语义的基础上，利用公式的可满足性建立粒化准则。U为论域是n元公式，则Un中所有满足φ的n元组构成集为φ的语义集，记作即所有满足公式φ的n元组都是从Un中分离出来的。公式φ恰好描述了元素之间的某种性质，因此将Un看作整体时，语义集合|φ|则表示整体中的一部分。

定义1设U为论域，Form（U）是U上所有公式的集合，称〈U，Form（U）〉为对应于论域U的粒空间。对任意的称φ为粒空间〈U，Form（U）〉上的公式，并将φ的语义集|φ|称为粒空间对应公式φ的粒，φ称为粒|φ|相对应的公式。

在粒空间〈U，Form（U）〉存在的公式恰好是粒的抽象表现，所以我们称之为抽象粒。为了将粒的概念进行区分，就将其他特定领域分离出的粒称作特定粒。抽象粒定义作为基础，利用逻辑公式作为工具进行粒层概念的定义，即抽象出的粒的全体就可以构成一个新的论域，这个新论域称之为粒层（或粒世界）。在公式空间中，使用具有某种语义性质的公式可以得出相关性质的粒层。

定义2 U为论域，Form（U）是U上所有公式的集合。若则由F（U）中全体公式形成的规则就形成|F（U）|（即全体公式语义集），|F（U）|就可以叫做一个粒层（粒层是粒集合的集合），表示为

在完整的粒层系统中，需要建立一套抽象的粒化方法来定义层与层之间的关系，从而表示其中的显性或隐性联系。这样正好符合多角度多方法的实际问题求解方式，其目的是为了达到简化和优化的效果。下面首先定义了一元和二元情况下的粒层的转换运算定义。

定义3 U为论域，φ∈Form（U）是二元公式，表示为φ（u，v），其中公式集合

表示U上满足公式φ（u，v）的粒层，另有U上的集合X，X⊆U，对x，y∈U，存在以下运算：（其中G（x）表示与x满足公式所构成的粒层；G′（x）表示与x不满足公式所构成的粒层）

我们将满足（1）、（2）的运算统称为上的粒类运算。

2 粒类运算中等价关系与分明关系互逆关系

从定义3可以看出，粒类运算x◦|P|说明运算结果中的每个元素都与满足公式P，X◦|P|说明其运算结果中每个元素都与论域U的子集X中的某一个元素满足公式P；而粒类运算|P|*y则说明运算结果中每个元素都与y不满足U公式P，|P|*X说明其运算结果中每一个元素都与X中的任意元素都不满足公式P。

粒类运算既定义了满足公式的运算，还定义了不满足公式的运算。而且这两类运算间存在互逆运算操作。也就是存在论域U，有公式则可以证明得到

利用信息系统的例子来说明粒类的◦和*的互逆操作，给定信息系统如下信息表：

表1 信息表1

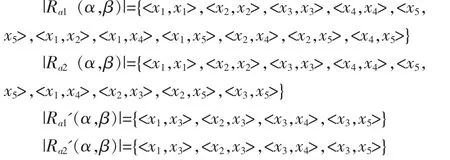
根据定义3，对元素x2，x4应用类运算◦和*，结果如下：

其他的元素运算方法和结果都和这两个的运算是一样的。

3 结语

从抽象粒出发，结合逻辑和代数运算定义的粒层粒类运算，属于粒计算的范畴，从而丰富了抽象粒模型。而且我们利用信息系统的等价关系和分明关系，说明o，*这两种粒类运算是一对互逆运算，从而说明粒层中粒之间会保持一定的不变性。因此在这方面说明了它们在处理实际问题时，具有应用的前景。

[1]Yan Lin，LiuQing.Formalization for Granular Computing Based on Logical Formulas.The Proceedings International Forum on Theory of GrC from Rough Set Perspective（IFTGrCRSP2006）.Journal of Nanchang Institute of Technology.Jun.2006.Vol.25.No.2：60-65.

[2]Yan Lin，Wang Sui-hua，Zhang Xue-dong.2006.Semantic Reasoning Study for Rough Logic about Nary Formulas.The Proceedings of 2006 IEEE International Conference on Granular Computing.Atlanta，Georgia，USA:381-384.

[3]Yao Y Y.2005.Perspectives of Granular Computing.The Proceedings of 2005 IEEE International Conference on Granular Computing. Beijing，China:85-90

[4]Yao，Y.Y.Three Perspectives of Granular Computing.Journal of Nanchang Institute of Technology，25，16-21，2006.

[5]Yao，Y.Y.The Art of Granular Computing.Lecture Notes in Artificial Intelligence，4585，101-112，2007.

[6]陈光，钟宁，姚一豫，黄佳进.粒计算中粒度转换的运算符.计算机科学，2011，38（12）：209～212

Research on Granular Inter-Reverse Operation Based on Logic Formula

JIN Rui-xia，ZHU Yun-feng，DU Xin-xin
（Sanquan Medical College，Xinxiang Medical University，Xinxiang 453000）

Granular computing is regarded as a methodology of understanding the objective world.It is a computational thinking mode of problem solving.On this basis,defines and explains the granular computing of abstract granule as inter-reverse operation according to Granular computing based on logical semantics.The conclusion can be obtained by applying different operations to the complementary relation.The research uses the equivalence relation and clear relation in the information system to analyze and illustrate the example,which shows that when faceing the same problem,there can be a best solution with a more appropriate way according to the certain condition.

Granule;Granular Computing;Reciprocal Relation;Complementary Relation

1007-1423（2017）09-0051-03

10.3969/j.issn.1007-1423.2017.09.013

靳瑞霞（1973-），女，河南漯河人，硕士，研究方向为计算机教育教学、多媒体、计算机网络

2016-12-27

2017-02-10

朱云峰（1981-），男，河南新乡人，本科，研究方向为计算机教育教学、计算机网络

杜新欣（1983-），女，河南新乡人，本科，研究方向为计算机教育教学、多媒体