基于地震偶极子波多重积分的初始阻抗模型建立方法

杜斌山， 贺振华， 王绪本 ， 雍学善, 刘应如

(1.成都理工大学 地球物理学院，成都 610059；2.中国石油勘探开发研究院 西北分院，兰州 730020)

基于地震偶极子波多重积分的初始阻抗模型建立方法

杜斌山1，2， 贺振华1， 王绪本1， 雍学善2, 刘应如2

(1.成都理工大学 地球物理学院，成都 610059；2.中国石油勘探开发研究院 西北分院，兰州 730020)

地震阻抗反演需要适当的低频储层模型，常规反演方法是基于地震、测井资料和地震速度预测来建立储层低频模型。由于储层纵横向变化快，常规方法易出现低频模型的多解性和精度低等问题。综合考虑储层顶底地震反射界面阻抗和储层厚度特征，提出了整体反映这些特征的地震偶极子波概念和相应的地震响应特征分析方法。以此为基础，形成了偶极子波多重积分约束的地震反演初始模型建立新方法。该方法充分利用地震多重积分对储层位置和厚度识别与表示功能，再结合测井声波曲线的分频谱等数据构建地震初始阻抗低频模型。该建模方法在柴达木盆地某工区实际应用结果表明，所建模型与实际复杂的风化壳裂缝储层地震剖面吻合好，较完整地反映了地震剖面上的地质层位与构造特征，该模型对提高地震反演的稳定性和精度十分有利。

地震偶极子波； 多重积分； 频谱特征； 储层厚度； 初始阻抗模型

0 引言

在油气储层预测中，地震反演技术应用较为广泛。其类型有递推反演、测井约束地震反演、线性和非线性反演等多种，地震反演的小波变换与遗传算法和神经网络算法都是非线性的。雍学善[1]等提出了逐道遗传外推的反演方法；孟宪军等[2]提出地震反演的精度与地震资料的品质、层位和断层解释的精度以及地层沉积模式与地层接触关系等都有紧密相关；崔岩等[3]指出初始模型建立对提高储层预测的效果非常重要。现阶段储层地震波阻抗反演存在的主要问题是常规波阻抗反演预测储层时只简单运用地震速度和测井声波资料建立低频初始模型，多解性较强。

实际上，对砂泥岩薄互层、碳酸盐岩、火山岩等特殊储层来说，地震预测存在分辨率低、多解性强两大关键问题[4-5]。对非均质储层预测精度和薄储层的分辨率方面要求更高，但随着预测分辨率的提高，各种预测方法以及迭代算法等都有较强的要求，会加入更多的人为信息，测井资料处理、井震标定和层位解释的精度都会影响反演结果，造成反演的多解性。为了克服地震预测的不确定性及多解性，世界上各大软件研发公司和学者相继对频谱分解、地震属性分析、小波分析、叠前分频AVO等方法技术进行了认真研究[6-12]，但效果并不太理想，还是具有较强的多解性。

笔者提出了一种基于偶极地震子波多重积分约束的储层初始阻抗模型建立的方法(DWMIC)。该方法把储层顶、底双反射系数，储层时间厚度及其偶合波形作为一个基本完整研究单元，再结合测井和地震资料的频谱特征，构建储层初始阻抗模型与地震波形、能量和多重积分变化的模型，在地震波形相关分析与多重积分约束下实现地震数据初始阻抗模型建立，最终形成一种适用于非均质储层的偶极子波多重积分约束的地震反演初始阻抗模型建立新方法。

1 模型建立方法原理

1.1 偶极子与地震偶极子波

关于偶极子的概念[13]，应用地球物理百科词典的作者Robert. E. Sheriff定义偶极子(Dipole)为“距离无限接近、电量相等的一对电荷或者是距离无限接近、极性相反的一对电极”。按此定义，在数学上，可将偶极子d(x) 表示为式(1)。

d(x)=q(x)+a·q(x-b)

a=±1,b→0

(1)

式中：q(x)为电荷或者极性场；a=1对应关于电荷的偶极子，a=-1对应关于电极的偶极子；b为两极之间的距离，对于应用地球物理勘探的实际问题，b→0是不可能存在的，在地震记录中，由于较薄储层顶、底之间的时间距离(一般为数十毫秒)远小于地震记录长度L(一般为数千毫秒)，可以近似假设距离b→0而不会带来明显误差，从而认为它们是偶极子。我们把对应于薄层(地层)顶、底的一对反射系数视为偶极子，定义其地震响应为地震偶极子波，其数学表示式如式(2)所示。

W(t,b)=W(t)+f·W(t-b)

f∈R,b→0

(2)

式(2)为地震偶极子波与反射系数褶积合成地震记录的计算模型。其中，S(t)为地震记录(合成地震记录)，t为时间，b为地层顶底反射系数之间的时间差，W(t,b)表示为地震偶极子波函数，R(t,b)为储层反射系数，R为实数。f=1，等价于前面公式a=1的情况，f=-1，等价于R(t,b)=Rt(t)的情况。但是f不再局限于正负1的特定值，而是任意实数。因此，可称偶极子波为扩展偶极子。扩展的目的是为了使薄层(或地层)的上下接触层的岩性任意变化，以适应各种复杂的接触关系，并简称扩展偶极子波为偶极子波，R(t,b)为储层反射系数。当储层厚度b=λ/4时，达到谐振。储层反射系数为式(3)。

R(t,b)=Rt(t)

(3)

式(4)为单个地震子波表达式[14]。

W(t)=Ae-β(f*(t-τ))2sin(2πfi)

(4)

式中：w表示为地震子波；i为时间域函数；A为子波最大振幅；f为地震子波的主频；β为衰减系数；τ为延迟时。

针对单个储层顶、底反射系数的极性特征，可分为4类见图1。

图1 储层顶底阻抗的四种组合模式及其对应地震响应特征(偶极子波)Fig.1 Four kinds of reservoir top and bottom interface impedance models and the corresponding seismic responses(seismic dipole wavelet )(a)储层顶底阻抗的四种组合模式； (b)对应地震响应特征

图1(a)为四个储层模型结构，其中(1)、(2)为顶底反射系数极性相反的组合形式，(3)、(4)为顶底反射系数极性相同组合形式。图1(b)为模型对应的地震偶极子波。地震偶极子波的波形有时比较简单(凸、 凹型)，有时相对复杂(上、下台阶型)。

基于偶极地震子波的储层初始阻抗模型建立方法的特点:①把储层顶、底界面双反射系数特征、储层厚度等信息整体融入地震响应特征(偶极子波)中。而偶极地震子波的精确构建首先需要通过测井、地震资料和井-震标定等技术获得储层顶、底界面的反射系数或者波阻抗信息以及地层厚度信息;②偶极地震子波包含的时间厚度信息以及层位信息，可通过对含有偶极子波地震道的积分或者多重积分来预测或者表示;③由于采用了偶极子波和多重积分方法，DWMIC有利于低频建模和消除随机噪音，从而提高反演的多解性和稳定性。

1.2 基于地震多重积分的阻抗数据转换

通常地震道积分是通过地震反射系数的积分求和，实现地震数据转换为地震相对阻抗剖面，是波阻抗反演的重要方法之一，且应用广泛[15]。地震多重积分是指对(合成)地震记录进行多轮次的地震道振幅累加运算，即从起始t0时间开始不断累加地震振幅的数值，在时间t进行记录，得到一个新的数据体，在t0～t区间累加地震振幅的次数即为积分的重数。多重积分的表达式如下：

sm(t)=∫m∫s(t)dt

(5)

k=(N-1)，(N-2),…2,1,0

(6)

式(5)为偶极地震子波多重积分表达式。其中，S(t)为地震记录，m为积分重数,sm(t)为积分结果。

在多重积分的离散式(6)中，N为数据总样点数，n为当前位置计算时间样点数，Δt为采样间隔，k为正整数。在式(6)中，规定s0(nΔt)为原始地震记录或者子波。

图2为一顶、底反射系数相等但极性相反的地震偶极子波的五重积分，图2(a)为偶极子波，图2(b)为其五重积分图。五重积分的主瓣能量突出，能较好地反映地层的实际位置和地层厚度(两红线之间)，体现了多重积分的基本功能。需要特别注意的是多重积分重数的选择和保证获得良好积分效果的数据处理方法：①在利用式(6)进行的多重积分计算时,其偶次积分结果中包含随时间增加而增大的异常低的低频分量，必须通过平滑滤波，加以消除，然后进行相应的奇数次积分；②建模过程中，我们常采用奇数次积分，这是因为一重积分(即通常的道积分)是对地震振幅数据进行累加运算，反映地震相对阻抗特征，且存在90°相位转换， 使其主瓣能量与储层所在位置对应，便于地震地质解释[16]。二重积分，是在一重积分的基础上对地震响应数据进行积分运算，存在两个(或者偶数次)90°相位转换。因此，偶数重积分反映的是反射界面特征，而经过三个(奇数个)90°的相位转换后，其结果又具有相对阻抗特征，但符号相反。所以奇数重积分反映储层相对阻抗特性，这正是阻抗反演和阻抗建模所需要的。

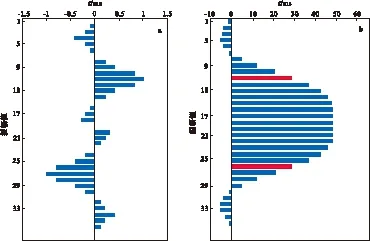
图2 偶极子波地震记录和偶极子波5重积分Fig.2 Seismic dipole wavelet (left) and its 5th multiple integral (right)(a)偶极子波；(b)五重积分图

1.3 地震多重积分与地层位置和厚度的对应关系

为了明确多重积分与地层位置和厚度的对应关系，我们制作一个储层厚度不同，隔层厚度变化的水平分层地质模型。从上到下储层时间厚度(ms)分别为：90ms、80ms、70ms、60ms、50ms、40ms、30ms、20ms、10ms、5ms、2.5ms,见图3(d)。对该模型用50HzRicker子波制作合成地震记录，1/4波长相当于10ms时间长度。对合成地震记录分别进行一、三、五重次积分的结果示于图3(a)、图3(b)和图3(c)。若从能否识别顶、底界面的分辨能力来看，一重积分结果能辨识10ms薄层，相当于1/4波长；三重积分结果能辨识30ms储层，相当于3/4波长储层厚度；五重积分也能辨识70ms储层，相当于7/4波长储层，但对储层位置和厚度的表示和识别而言，则积分重数多的效果更好，因此可用多重积分结果直接进行相对地震阻抗建模。

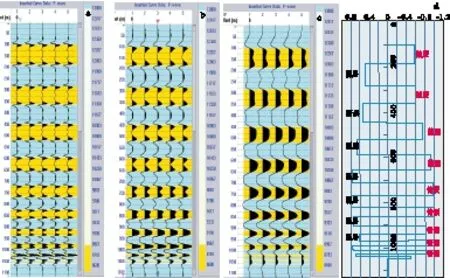
图3 多重积分与储层顶底反射位置和预测储层厚度图Fig.3 The seismic trace multiple integral and resrvoiv's top and bottom reflection interface impedances and predict thickness(a)合成记录的一重积分; (b)三重积分; (c)五重积分剖面;(d)储、隔层厚度模型

1.4 地震多重积分的频谱特征

为认识地震数据多重积分相对阻抗的频谱特征。我们需要对积分结果进行频谱分析。图4是同一合成地震记录的多重积分频谱。由图4可见，随着积分重数的增加，出现两个明显变化，频带愈来愈窄，主频愈来愈低，最低频率达到3Hz，说明高积分重数的结果对构建低频模型有利。

2 初始阻抗模型建立的基本步骤

基于偶极子波和多重积分进行初始阻抗模型构建包括以下关键步骤：

1)测井基础数据分析与整理。首先从单井测井资料解释中获取准确反映储层地震响应特征的有关参数，然后在充分利用地震、测井和录井资料的基础上，结合钻井、测井资料提取储层厚度信息以及储层上下介质的声波、密度和波阻抗等储层信息。采用大层位标定、分频标定、合成记录精细标定等技术手段，提取最优地震子波，同时利用地震地质分层、地震解释层位以及波形特征等多种信息获得最佳的时深关系。

2)基于地震多重积分的相对阻抗预测。获取井点处储层的偶极地震子波响应特征函数，对其进行地震多重积分运算。对多个井点处地震多重积分结果进行比较，最终确定适合该区的最佳滑动时窗长度和积分重数等计算参数。一般来说，积分计算时窗越大，低频成分越多；计算时窗越小，高频成分较丰富。 利用所确定的最佳计算参数和滑动时窗长度对实际工区的地震数据体进行地震多重积分运算，以生成相对阻抗预测数据体。

图4 同一地震数据的多重数积分频谱特征Fig.4 Seismic multiple integral frequency spectrum characteristics of the same seismic data(a)一重积分频谱；(b)三重积分频谱；(c)五重积分频谱； (d)七重积分频谱；(e)九重积分频谱；(f)十一重积分频谱

3)测井阻抗数据的分频段滤波。对测井阻抗曲线进行不同带宽的频率滤波，获得分频测井阻抗曲线。由于该曲线与地震道不同次数的重积分结果有相似性，可为井-震资料的有效结合提供依据。

4)多重积分与地震速度初始阻抗模型建立。地震数据多重积分转换的相对阻抗频谱特征具有明显分段性(见图4和图5)，通过结合地震连续速度谱预测的频谱，将其叠加(合并)，可逐步逼近测井资料的宽带阻抗频谱，并保持原始地震频谱中低频信息的完整性，为低频建模做好准备。在图5中，d1井井旁地震道速度谱的频谱带宽为0Hz～3Hz，井旁地震道五重积分谱的带宽为3Hz～7Hz，地震道三重积分具有7Hz～14Hz的频谱特性，地震道一重积分具有14Hz～48Hz的频谱特性，一重积分与地震道频谱(12Hz～4 8Hz)有一定的相似性，于是形成了一个具有完整的连续的低频特征的频谱系列，有效凸显3Hz～40Hz的隐蔽信息。

3 应用实例分析

为检验上述方法的效果，下面结合柴达木盆地某工区地震偶极子波多重积分阻抗建模的例子，说明建模的具体方法与效果。根据该区d1井等钻井情况看，有多口井在储层段获得工业气流，储层类型为基岩风化壳裂缝型。测井曲线表现出高声波时差储层特征[17-18]，d1井有多段储层，其中目的层段压裂试气后，获高产天然气。在该区建模有以下步骤：

1)需要进行测井-地震资料特征分析(如对d1关键井进行精细井震标定，利用井震资料联合提取子波，并得到最佳的时-深关系和最优子波，以获得高质量合成记录)。对井旁地震剖面进行多重积分，并进行谱分析，获得地震频谱基本特征。图6显示了上述资料的综合特征。为下一步研究提供基础。

2)构建不同频谱特征的储层模型。如图7所示，测井曲线储层段的声波频谱特性及地震速度谱的频谱特征之间有一定的相似性，但是地震频谱缺乏低频段信息，测井反射系数的频谱也缺乏低频分量，而地震速度频谱的低频成分丰富，它们之间又有一定的互补性。将这些特征相结合，对建立具有连续频谱特性的模型十分重要。

3)进行合成地震记录多重积分与测井分频阻抗的计算，确定它们之间的相关性(图8)。除个别道外，总体上多重积分相对阻抗结果与不同频段的分频滤波结果具有相似性。考虑到多重积分结果在频率域具有分段性，可以将多个多重积分的频谱合并，如图9(b)所示。同理，也可将测井阻抗分频谱合并，得到图9(c)所示的结果。图9(b)、图9(c)在有效频段较为相似，地震多重积分合并数据频谱与测井分频合并的相对阻抗数据较为相似，说明地震多重积分相对阻抗预测有较好的效果。

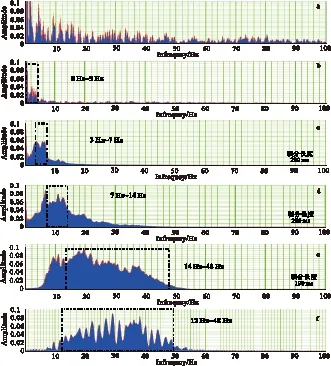
图5 偶极子波地震多重分频谱、地震速度频谱特征对比图Fig.5 The comparisons among seismic data spectrum, multiple integral and seismic velocity spectrum(a)测井数据频谱；(b)地震速度谱的频谱；(c)五重积分； (d)三重积分；(e)一重积分；(f)地震数据频谱

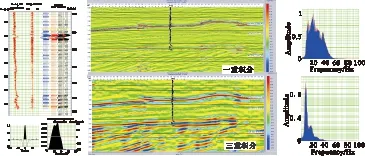
图6 d1井合成记录标定图及多重积分剖面图Fig.6 The well d1 synthetic seismogram calibration and multiple integral sections

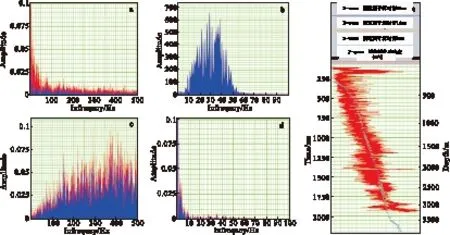
图7 测井阻抗-地震速度数据频谱特征分析Fig.7 The comparisons among well logging impedance spectrum, seismic velocity frequency spectrum and seismic data spectrum(a)测井波阻抗频谱(0.1ms)；(b)地震数据频谱；(c)测井反射系数频谱(0.1ms)； (d)地震速度频谱；(e)地震速度转换层速度

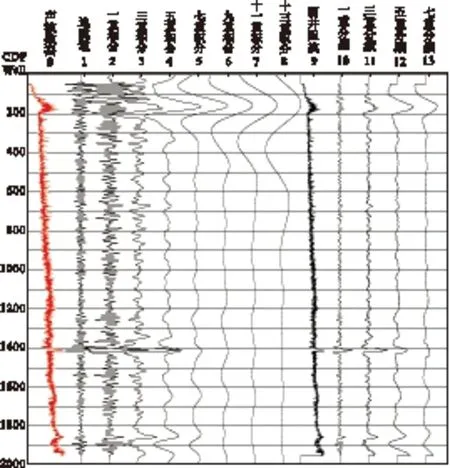
图8 d1井合成地震记录多重积分与测井分频滤波结果对比图Fig.8 The comparisons of seismic multiple integral traces and well logging fractional filter traces

4)建立相对阻抗初始模型。由于偶极地震子波和储层地震响应的多重积分均包括地层厚度和层位信息。因此基于地震偶极子波多重积分的初始阻抗模型可以直接在经过前述处理的地震剖面上建立，而无需输入常规地震层位和地层厚度。图10为一重积分相对阻抗剖面图。图11为多重积分合并的相对阻抗剖面。多重积分剖面合并后，低频特征较为清晰，剖面背景更清楚，能够很好地反映目的层基岩风化壳地质特征。

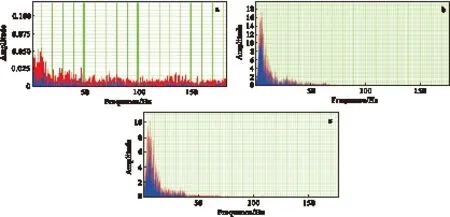
图9 测井阻抗频谱与合并相对阻抗数据频谱对比分析图Fig.9 The comparisons among well logging impedance spectrum, seismic multiple integral spectrum and well logging fractional filter trace spectrum(a)原始测井阻抗数据频谱图；(b)多重积分数据合并相对阻抗频谱图； (c)测井分频阻抗数据合并相对阻抗频谱图

图10 地震一重积分相对阻抗数据剖面模型Fig.10 The seismic 1st integral relative impedance section model

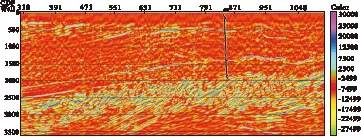
图11 地震一、三、五、七重积分合并相对阻抗剖面模型Fig.11 The seismic relative impedance section model by stacking the 1st,3rd ,5th and 7th multiple integral profiles

图12为地震一、三、五、七重积分合并相对阻抗数据与地震速度合并剖面图，加入地震速度频谱的低频成分后，初始阻抗剖面模型能较全面地反映基岩顶面特征。由于该初始模型与实际地震剖面十分接近，完全不是常规线条型模型样式，因此，有助于降低最终的地震参数反演的多解性，提高反演的稳定性。

图12 地震一、三、五、七重积分合并相对阻抗数据与地震速度合并的初始阻抗模型Fig.12 The stacking relative impedance section model with seismic 1st, 3rd ,5th and 7thmultiple integral profiles and seismic velocity analysis

4 结论

1)笔者提出的基于地震偶极子波多重积分的初始阻抗模型建立方法，充分挖掘了地震记录蕴含地震地质信息，综合考虑储层偶极子波的响应特征、偶极子波双反射系数整体波形特征，提高了储层预测可靠性，有利于降低反演的多解性。

2)明确了地震多重积分储层的含义，构建了地震偶极子波多重积分数学表达式，明确了储层顶底界面反射系数估算以及多重积分相对阻抗与地层界面的奇偶特性，证实地震奇数重积分具有相对阻抗预测的效果。

3)地震数据多重积分相对阻抗的频谱特性具有明显分段性，结合地震资料速度预测，采用多重积分合并预测相对阻抗，逐步逼近储层阻抗频谱，提高低频模型预测效果，提高了初始模型建立的精度。

[1] 雍学善, 余建平, 石兰亭.一种三维高精度储层参数反演方法[J].石油地球物理勘探,1997，32(6):852-856.YONGXS,YUJP，SHILT.Anaeeuratemethodfor3-DreservoirParameterinversion[J].OGP,1997,32(6):852-856.(InChinese)

[2] 孟宪军，金翔龙，钮学民,等.地震反演中的三维复杂约束模型[J].石油大学学报(自然科学版),2004, 28(6):21-26.MENGXJ,JINXL,NIUXM.Researchof3-Dcomplexconstrainedmodelinseismicinversion[J].JournaloftheUniversityofPetroleum，2014, 28(6):21-26.(InChinese)

[3] 崔岩, 王彦飞, 杨长春. 带先验知识的波阻抗反演正则化方法研究[J].地球物理学报,2009，52(8)：2135-2141.CUIY,WANGYF,YANGCC.Regu1arizingmethodwithaprioriknow1edgeforseismicimpedanceinversion[J]．ChineseJ.Geophys，2009,52(8): 2135-2141.(InChinese)

[4] 雍学善. 砂泥岩薄互层储层预测的难点与对策[J]. 天然气工业，2005，25(增B)：96-100.YONGXS.Difficultiesandcountermeasurestopredictreservoirswiththinsand-shalealternatinglayers[J].NaturalGasIndustry，2005,25(SB):96-100.(InChinese)

[5]WIDESSM.B.Howthinisathinbed[J].Geophysics, 38(6):1176-1180.

[6]PIERRETHORE,OLIVIERDUPLANTIER，YUNQUIXU. 2Seismicinversionuncertainty:whatdoesreallymatter[C].2013SEGHoustonAnnualMeeting.

[7]CHARLESI.PURYEAR,JOHNP.CASTAGNA.Layer-thicknessdeterminationandstratigraphicinterpretationusingspectralinversion:Theoryandapplication[J].Geophysics，2008，73(2):37-48.

[8]WANGX,ZHANGYQ.Pre-stackinversioncombinedwithgeostatisticalsimulationtopredictthinreservoirs[C]. 2010SEGDenverAnnualMeeting，2010.

[9]WHITCOMBEDN.Elasticimpedancenormalization[J].Geophysics,2002,67(1):63-67.

[10]刘晓晶, 印兴耀, 吴国忱,等.基于正交匹配追踪算法的叠前地震反演方法[J].石油地球物理勘探，2015,50(5):925-935.LIUXJ，YINXY，WUGC，etal.ZongZhaoyun;Prestackseismicinversionbasedonorthogonalmatchingpursuitalgorithm[J].OilGeophysicalProspecting,2015,50(5):925-935.(InChinese)

[11]马劲风. 地震勘探中广义弹性阻抗的正反演[J]. 地球物理学报,2003, 46(1)：118-124.MAJF.Forwardmodelingandinversionmethodofgeneralizedelasticimpedanceinseismicexploration[J].ChineseJournalofGeophysic. 2003, 46(1)：118-124.(InChinese)

[12]CONNOLLY.Elasticimpedance[J].TheLeadingEdge,1999, 4:438-452.

[13]ROBERT.E.SHERIFF.Encyclopedicdictionaryofappliedgeophysics,FourthEdition[C].SEG,TulsaOklahoma,USA,2006.

[14]雍学善, 吴胜和.储集层厚度谱的建立及其意义[J].新疆石油地质,2005,26(6):647-649.YONGXS,WUSH.EstablishmentandSignificanceofReservoirThicknessSpectrum[J].XinjangPetroleumGeology,2005,26(6):647-649.(InChinese)

[15]陆基孟. 地震勘探原理[M]. 北京:石油大学出版社，1996.LUJM.Principleofseismicexploration[M].Beijing:petroleumuniversitypress,1996.(InChinese)

[16]HONGLIUZENG.Seismicanalysisofverythinbeds:whichattributetouse[C]. 2012SEGAnnualMeeting. (phaseandfrequencyslices)

[17]贺振华, 邓英尔, 刘树根，等.岩石弹性参数对渗流测试分析的影响[J]. 天然气工业，2006，26(6):44-46.HEZH,DENGYE,LIUSG,etal.Influenceofrockelasticparametersontestanalysesofflowinrock[J].NaturalGasIndustry,2006,26(6):44-46.(InChinese)

[18]贺振华, 黄德济, 文晓涛.裂缝油气藏地球物理预测[M]. 成都:四川科学技术出版社，2007.HEZH,HUANGDJ,WENXT.Fracturedreservoirgeophysicalprediction[M].Chengdu:Sichuanscienceandtechnologypress,2007. (InChinese)

Initial impedance model establishment based on the seismic dipole wavelet and multiple integral methods

DU Binshan1,2, HE Zhenhua1, WANG Xuben1, YONG Xueshan2, LIU Yingru2

(1.Chengdu university of technology Geophysical Institute，Chengdu 610059， China；2.Chinese petroleum exploration and development research institute ，northwest branch,Nanzhou 730020， China)

The seismic impedance inversion requries a proper low-frequency reservoir model. The conventional inversion method is based on logging data and seismic velocity prediction to establish reservoir low-frequency model. Due to the reservoir parameters horizontally and vertically quickly change, the uncertainty and low precision of the seismic inversion by using conventional low frequency model are not avoidable. In order to overcome these problems, a dipole wavelet multiple integral constraint method (DWMIC) for seismic inversion initial model establishment is proposed in this paper. The seismic dipole wavelet of a reservoir is a comprehensive representation of reservoir's top and bottom reflection interface impedances and thickness and the seismic trace multiple integral combined well logging acoustic fractional spectrum data can obtain reservoir positions and seismic impedances. The DWMIC modelling method has been applied to a work area in Qaidam basin. The result shows that the model constructed by the DWMIC fits the real seismic profile quite well for a complex weathering crust fracture reservoir. It means the model can be fully reflected the geological horizon and structure characteristics on the seismic section, suggesting that it is possible to improve the stability and precision of seismic inversion.

seismic dipole wavelet; multiple integral; spectrum characteristics; reservoir thickness; initial impedance model

2016-11-02 改回日期：2016-12-21

国家自然科学基金(41374111);国家重大专项(2016zx05007-006);柴达木重大专项(2016E-03)

杜斌山(1970-)，男，博士，主要从事地震反演、储层预测、油藏描述等方面研究,E-mail：dubs@petrochina.com.cn。

1001-1749(2017)01-0071-10

P 631.4

A

10.3969/j.issn.1001-1749.2017.01.11