外置拉紧装置的带式输送机动态特性
2017-05-11周广林李阳星聂文明
周广林,李阳星,聂文明
(黑龙江科技大学 机械工程学院,哈尔滨150022)
外置拉紧装置的带式输送机动态特性
周广林,李阳星,聂文明
(黑龙江科技大学 机械工程学院,哈尔滨150022)
随着带式输送机向着大型化的方向发展,动态特性对其运行的稳定性与安全性的影响效应增大,对带式输送机动态特性规律的研究成为保证其安全可靠运行的关键问题之一。基于复杂系统建模仿真平台Amesim,搭建了外置拉紧装置的带式输送机的虚拟样机模型,研究了启制动时间、运行速度对带式输送机的动态特性影响的变化规律,得到输送带达到破断张力时启制动时允许的最短时间、最高运行速度。同时,分析了输送距离、输送带阻尼和输送带刚度对带式输送机动态特性影响的变化规律。该研究为大型带式输送机的设计和使用提供理论依据。
带式输送机;动态特性;拉紧装置;Amesim
0 引 言
带式输送机作为一种连续运输设备,越来越受到使用者的青睐,特别是随着各种特种带式输送机的出现以及带式输送机的大型化,其适用范围越来越广[1,2]。
动态分析技术是大型带式输送机设计的技术关键之一,是推动带式输送机向着大运量、长运距、高带速的大型化方向发展的核心技术。动态分析技术的应用,可提高带式输送机运行的可靠性,预防事故的发生,因此,对大型带式输送机进行动态特性分析成为带式输送机研究的热点之一。
郝双双[3]对带式输送机启制动过程的动态特性进行了仿真分析,得到带式输送机启制动阶段的动态特性与启制动时间的变化规律。孙文涛[4]对线摩擦驱动带式输送机的动态特性进行分析研究,得到启动运行参数和结构参数对线摩擦带式输送机动态特性的影响规律。韩瑞飞[5]讨论了输送带刚度、阻尼系数、压辊分布以及带速对辊子压带式带式输送机动态特性的影响变化规律。吴彬[6]研究机架对带式输送机动态特性的影响。李晓辉[7]研究了弯曲运行段的托辊布置方式以及转弯曲率半径等参数对平面转弯带式输送机动态特性影响的变化规律。
拉紧装置是带式输送机必不可少的重要组成部分。但是,过去对带式输送机进行动态特性分析时,不是采用实体结构的拉紧装置,而是将拉紧参数内置于计算模型中(这里称之为内置拉紧装置)[8-10],笔者把拉紧装置作为实体结构模型的一部分(称外置拉紧装置),构建带式输送机虚拟样机模型,分析其运行参数和结构参数对外置拉紧装置带式输送机动态特性的影响,为合理设计带式输送机提供理论依据。
1 虚拟样机模型
设带式输送机的铺设长度为L,将输送带承载分支划分为M段,头部驱动滚筒设为第一个单元,按与带式输送机运行的相反方向,承载分支输送带的单元编号依次为:1,2,…,M,尾部改向滚筒的单元编号为M+l,将输送带回程分支划分为N个单元,从尾部开始,单元编号依次为:M+2,M+3,…,N+M,将重锤看做一个单元,编号为N+M+l。根据输送带两相邻点的黏弹性模型和对带式输送机单元的划分,建立外置拉紧装置带式输送机整机的离散化有限元模型,如图1所示。

图1 带式输送机离散化模型Fig.1 Discretization model of belt conveyor
根据以上对带式输送机离散模型基本单元受力分析,可以得到带式输送机的系统动力学方程[8]
(1)
式中:m1,m2,…,mN+M+1——第1,2,…,N+M+1个单元的质量,kg;
k1,k2,…,kN+M+1——第1,2,…,N+M+1个单元的刚度系数,N/m;
c1,c2,…,cN+M+1——第1,2,…,N+M+1个单元的阻尼系数,N/(m·s-1);
x1,x2,…,xN+M+1——第1,2,…,N+M+1个单元的位移,m;


F1,F2,…,FN+M+1——第1,2,…,N+M+1个单元所受到的驱动力,N;
f1,f2,…,fN+M+1——第1,2,…,N+M+1个单元所受的阻力,N。
将式(1)改写成矩阵形式:

(2)
在分析外置拉紧装置对带式输送机动态特性的影响变化规律时,仿真计算模型的具体参数驱动滚筒质量800kg;驱动滚筒半径1.2m;改向滚筒质量600kg;改向滚筒半径0.65m;承载段输送带及货载单元质量2 780kg;空载段输送带单元质量1 200kg;输送带承载段静摩擦阻力750N;输送带空载段静摩擦阻力460N;输送带承载段动摩擦阻力720N;输送带空载段动摩擦阻力430N;输送带宽度1.2m;拉紧重锤单元质量10 000kg。仿真步长为Δt=0.01s,数据监测点设在输送带和驱动滚筒相遇处的模型单元上。
2 运行参数对动态特性的影响
2.1 启动时间
设启动时间t0分别为6、8、10 s三种不同数值,输送带单元刚度系数1.817 3×107N/m;输送带单元阻尼系数1.643 2×107N/(m·s-1);输送距离1 200 m;运量2250 t/h;运行速度为v0=5 m/s,仿真时间设为t=13 s,动张力仿真曲线如图2所示。
当t0=10 s,动张力峰值在t=4.96 s时,峰值为314.9 kN;当t0=8 s,其动张力峰值在t=3.6 s时,峰值为378 kN,比t0=10 s时动张力峰值增加20%;当t0=6 s,动张力峰值在t=3.05 s时,峰值为469.8 kN,比t0=10 s时动张力峰值增加49.2%。由此可以看出,启动时间对输送带动张力峰值的大小影响较大,且启动时间越短,动张力峰值越大。
当启动的时间为t0=6.65 s,动张力峰值在t=3.21 s时,峰值为432 kN,达到了该输送带的破断张力值。由此可知,稳定运行速度为v0=5 m/s,带式输送机启动时间应保持在t0=6.65 s以上,才能保证设备的安全稳定运行。

a t0=10 s

b t0=8 s

c t0=6 s

d t0=6.65 s
2.2 制动时间
设制动时间tz分别为7、8、9 s三种不同数值,输送带单元刚度系数1.817 3×107N/m;输送带单元阻尼系数1.643 2×107N/(m·s-1);输送距离1 200 m;运量2 250 t/h;运行速度为v0=5 m/s,仿真时间为t=20 s,不同制动时间下的动张力仿真曲线如图3所示。
带式输送机的运行状态设置为先进行与制动时间完全相同的启动时间,完成启动过程后,进行时长为t=2 s的稳定运行,继而进入其制动阶段,即制动开始时的时间t分别为9、10、11 s。当Tz=7 s,动张力峰值在t=12.32 s时,峰值为-219.3 kN,停止运行时输送带中的静张力值为56 kN;当tz=8 s,动张力峰值在t=14.13时,峰值为-178.5 kN,比tz=7 s时动张力峰值减小18.6%,停止运行时输送带中的静张力值为65.2 kN;当tz=9 s,其动张力峰值在t=15.48 s时,峰值为-149.2 kN,比tz=7 s时动张力峰值减小32%,停止运行时输送带中的静张力值为71.6 kN。从图3中可以看出,制动阶段的动张力峰值远远小于启动阶段的动张力峰值,故在启动与制动时间相同时,在保证启动阶段可以安全稳定运行的情况下,制动阶段也可安全稳定运行。随着制动时间的延长,制动阶段的动张力峰值减小。

a tz=7 s

b tz=8 s
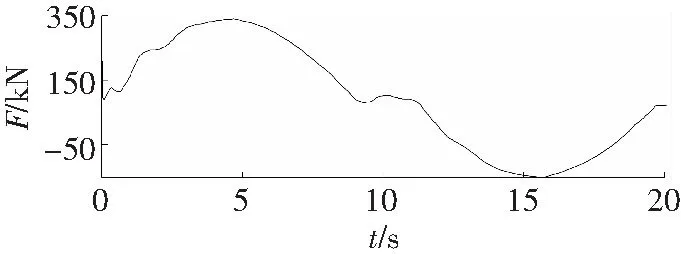
c tz=9 s

d tz=4.11 s图3 不同制动时间下的动张力曲线Fig.3 Dynamic tension curves under different braking time
当制动时间为tz=4.11 s,动张力峰值在t=13.24 s时,峰值为-432 kN,达到了该输送带的破断张力值,根据以上分析,制动时间应保持在tz=4.11 s时以上,才能保证设备的安全稳定运行。
2.3 输送带运行速度
设稳定运行速度v0分别为6、7、8 m/s时,,输送带单元刚度系数1.817 3×107N/m;输送带单元阻尼系数1.643 2×107N/(m·s-1);输送距离1 200 m;运量2 250 t/h;启动时间t0=10 s,仿真时间为t=13 s,仿真动张力曲线如图4所示。
由图4可知,当v0=6 m/s,输送带动张力峰值在t=4.88 s时,峰值为358.2 kN,稳定动张力值为95 kN;当v0=7 m/s,输送带动张力峰值在t=4.88 s时,峰值为401.9 kN,比v0=6 m/s时动张力峰值增加12.2%,稳定动张力值为95.1 kN;当v0=8 m/s,输送带动张力峰值在t=4.88 s时,峰值为445.6 kN,比v0=6 m/s时动张力峰值增加24.4%,稳定动张力值为95.2 kN。由此可知,在稳定运行时,不同带速稳定动张力值基本一致,峰值则随着带速的提高而增大。

a v0=6 m/s

b v0=7 m/s

c v0=8 m/s
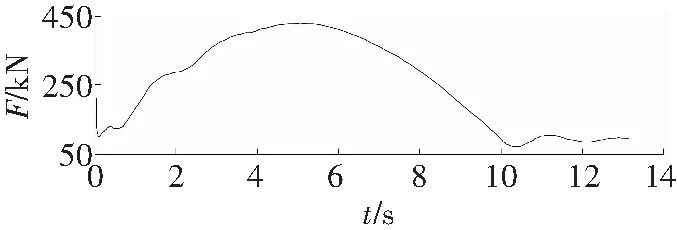
d v0=7.68 m/s图4 不同稳定运行速度下的动张力曲线Fig.4 Dynamic tension curves under different stable speed
当运行速度为v0=7.68 m/s,张力峰值在t=4.88 s时,达到432 kN,是该输送带的破断张力值,由此可知,运行速度应保持在v0=7.68 m/s以下,才能保证设备的安全稳定运行。
2.4 输送距离
取输送距离L分别为900、1 200、1 500 m三种不同数值,输送带单元刚度系数1.817 3×107N/m;输送带单元阻尼系数1.643 2×107N/(m·s-1);运量2 250 t/h;运行速度为v0=5 m/s,启动时间t0=10 s,仿真时间为t=13 s,仿真动张力曲线如图5所示。
由图5可知,当L=900 m,输送带动张力峰值在t=4.97 s时,峰值为224.8 kN,稳定动张力值为72.7 kN;当L=1 200 m,输送带动张力峰值在t=4.96 s时,峰值为314.9 kN,比L=900 m时动张力峰值增加40.1%,稳定动张力值为94.9 kN;当L=1 500 m,输送带动张力峰值在t=5.33 s时,峰值为413.8 kN,比L=900 m时动张力峰值增加84.1%,稳定动张力值为137.8 kN。对比数据可以看出,随着输送距离的增大,动张力峰值有较大幅度增加,稳定动张力值也有所增加。

a L=900 m

b L=1 200 m

c L=1 500 m图5 不同输送距离下的动张力曲线Fig.5 Dynamic tension curves under different transmission distance
3 结构参数对动态特性的影响
3.1 输送带阻尼系数
取输送带阻尼系数c分别为1.64 3 2×106、1.643 2×107、1.643 2×108N/(m·s-1)三种数值,输送带单元刚度系数1.817 3×107N/m;输送距离1 200 m;运量2 250 t/h;运行速度为v0=5 m/s,启动时间t0=10 s,仿真时间为t=40 s,仿真动张力曲线如图6所示。
由图6可见,当c=1.643 2×106N/m·s-1时,输送带动张力峰值在t=4.95 s时,峰值为347.2 kN,稳定动张力值为94.8 kN;当c=1.643 2×107N/ m·s-1时,输送带动张力峰值在t=4.96 s时,峰值为314.9 kN,比c=1.643 2×106N/m·s-1时动张力峰值减小9.3%,稳定动张力值为94.9 kN;当c=1.643 2×108N/m·s-1,输送带动张力峰值在t=5.01 s时,峰值为313 kN,比c=1.643 2×106N/m·s-1)时动张力峰值减小9.8%,稳定动张力值为94.7 kN。
由此可以看出,随着阻尼系数的增大,输送带动张力峰值减小,而稳定运行时的动张力基本趋于一致。对比三种不同阻尼系数时的动张力曲线,随着阻尼系数的增大,动张力值的波动幅值及频率呈下降趋势,并且动张力峰值出现的时间点向后延迟,但延迟的时间较短。
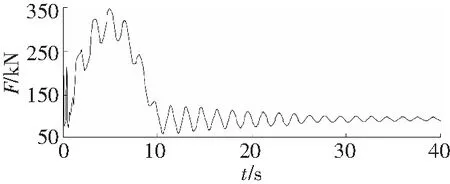
a c=1.643 2×106 N/m·s-1

b c=1.643 2×107 N/m·s-1
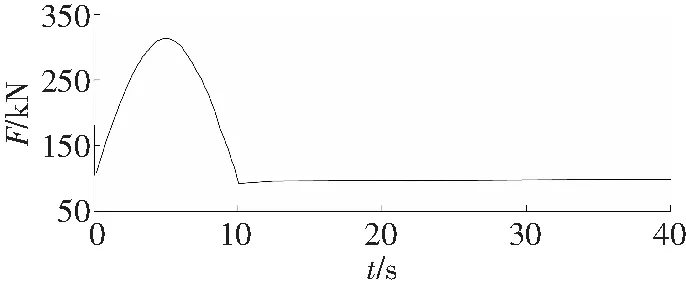
c c=1.643 2×108 N/m·s-1
3.2 输送带刚度系数
取输送带刚度系数k分别为1.817 3×106、1.817 3×107、1.817 3×108N/m三种数值,输送带单元阻尼系数1.643 2×107N/m·s-1;输送距离1 200 m;运量2 250 t/h;运行速度为v0=5 m/s,启动时间t0=10 s,仿真时间为t=13 s,仿真动张力曲线如图7所示。
由图7可知,当k=1.817 3×106N/m,输送带动张力峰值在t=5.62 s时,峰值为343.7 kN,稳定动张力值为95 kN;当k=1.817 3×107N/m,输送带动张力峰值在t=4.96 s时,峰值为326.6 kN,比k=1.817 3×106N/m时动张力峰值减少4.98%,稳定动张力值为95 kN;当k=1.817 3×108N/m,输送带动张力峰值在t=4.96 s时,峰值为314.9 kN,比k=1.817 3×106N/m时动张力峰值减少8.38%,稳定动张力值为94.9 kN。由此可知,随着刚度系数的增大,动张力峰值减小,动张力峰值出现的时间点延后,稳定运行时的动张力值基本一致。随着刚度系数的增大,输送带中的动张力值的波动幅值有所增加。

a k=1.817 3×106 N/m
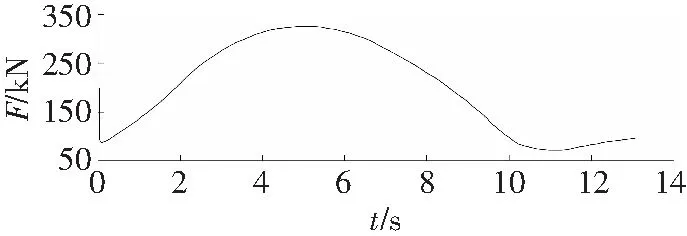
b k=1.817 3×107 N/m

c k=1.817 3×108 N/m
4 结 论
(1)随着启动时间的延长,输送带的动张力峰值随之减小。在带式输送机稳定运行速度v0=5 m/s时,其启动时间应保持在t0=6.65 s以上,以保证设备的安全稳定运行。
(2)随着制动时间的延长,制动阶段的动张力峰值随之减小。在带式输送机在稳定运行速度为v0=5 m/s时,其制动时间应保持在t=4.11 s以上,以保证设备的安全稳定运行。
(3)在稳定运行时,不同带速条件下的稳定动张力值基本趋于一致,而在启动阶段内的动张力峰值则随着带速的提高而增大。带式输送机的稳定运行速度应保持在v0=7.68 m/s以下,以保证设备的安全稳定运行。
(4)随着输送距离的增大,动张力峰值有较大幅度的增加,稳定运行时的动张力值也随之有所增加。
(5)随着阻尼系数的增大,输送带中的动张力峰值随之减小,而稳定运行时的动张力基本趋于一致,动张力值的波动频率呈下降趋势,动张力峰值出现的时间点向后延迟。
(6)随着输送带刚度系数的增大,动张力峰值减小,动张力峰值出现的时间点延后,稳定运行时的动张力值基本一致。
致谢:
该论文获得黑龙江科技大学研究生创新科研基金项目“拉紧装置的带式输送机动态特性研究(YJSCX2015-007HKD)”的支持。
[1] 张振文,宋伟刚.带式输送机工程设计及应用[M].北京: 冶金工业出版社,2015.
[2] 宋伟刚.特种带式输送机设计[M].北京: 机械工业出版社,2007.
[3] 郝双双.动态特性对带式输送机运行安全性的影响研究[D].哈尔滨: 黑龙江科技学院,2008.
[4] 孙文涛.线摩擦驱动带式输送机动态分析[D].哈尔滨: 黑龙江科技学院,2012.
[5] 韩瑞飞.辊子压带式带式输送机的动态特性[J].黑龙江科技大学学报,2014,24(1): 85-93.
[6] 吴 彬.考虑机架影响的带式输送机动态特性分析[D].哈尔滨: 黑龙江科技大学,2015.
[7] 李晓辉.平面转弯带式输送机动态特性分析[D].哈尔滨: 黑龙江科技大学,2015.
[8] 聂文明.包含拉紧装置的带式输送机动态特性研究[D].哈尔滨: 黑龙江科技大学,2016.
[9] 李阳星,李晓辉.基于ADAMS平面转弯带式输送机的动态特性[J].黑龙江科技大学学报,2015,25(5): 482-488.
[10] 张东升,毛 君,刘占胜.刮板输送机启动及制动动力学特性仿真与实验研究[J].煤炭学报,2016,41(2): 513-521.
(编辑 晁晓筠 校对 李德根)
Research on dynamic characteristics behind belt conveyor of external tension device
ZhouGuanglin,LiYangxing,NieWenming
(School of Mechanical Engineering,Heilongjiang University of Science & Technology,Harbin 150022,China)
The trend towards the development of the large-scale belt conveyor leads to an increased effect of the dynamic characteristics on its running stability and security,thus necessitating the research into the law underlying the dynamic characteristics of belt conveyor——the key to ensuring the safe and reliable operation.The study building on Amesim,one of a complex system modeling simulation platforms works towards the development of the virtual prototyping model of the external tension device and the investigation into the changing law behind the effect of starting and breaking time and running speed on the dynamic characteristic of belt conveyor.The research provides the shortest time and highest speed allowed for the conveyor belt as it reaches the breaking tension during the start-stop time and identifies the changing rule behind the effect of damping and transmission distance on the dynamic characteristics of belt conveyor.The work may serve as the theory basis for design and use of large belt conveyors.
belt conveyor; dynamic characteristics; tension device; Amesim
2017-02-10
周广林(1961-),男,吉林省怀德人,教授,博士,研究方向:机械系统动态特性分析技术、设备监测与可靠性技术,E-mail:guanglinzhou@163.com。
10.3969/j.issn.2095-7262.2017.02.008
TD528.1
2095-7262(2017)02-0133-06
A
