分布质量模型下的采煤机牵引部扭振系统动态特性及优化

张 丹，刘春生，王爱芳，任春平

(黑龙江科技大学 机械工程学院，哈尔滨 150022)

分布质量模型下的采煤机牵引部扭振系统动态特性及优化

张 丹，刘春生，王爱芳，任春平

(黑龙江科技大学 机械工程学院，哈尔滨 150022)

针对采煤机牵引部扭振引发各种故障问题，采用等效构件法，建立采煤机牵引传动系统扭振分析等效模型和轴段分布质量扭振数学模型，得到分布质量模型下采煤机扭振系统的传递矩阵、固有频率及振动模态。以各弹性轴段势能分布均匀性作为优化目标，以各弹性势能方差作为目标函数，利用降梯度算法对扭振系统进行了参数优化。结果表明：该矩阵在轴系纯扭系统中具有通用性，可以解决集中参数模型下扭振分析精度不足的问题；优化后，行星减速器输出轴和行走轮轴的弹性势能占比分别由原来的40%、41%降低到23%、22%，弹性势能均匀性明显提高，系统动态特性得到改善。研究结果为采煤机牵引部传动系统参数的确定及扭转动态特性的改善提供了理论依据。

采煤机；牵引传动系统；分布质量模型；传递矩阵；扭振模型；参数优化

0 引 言

采煤机牵引部担负着为采煤机提供前进方向动力的重要任务。由于激振力和激振力矩的作用，牵引部减速组件经常产生扭转振动。当系统的固有频率靠近扭振频率或与其重合时，传动系统扭转振幅会急剧增大，此时系统动态应力远远超出静态应力。随着采煤机向大功率方向发展，采煤机的牵引系统的扭振问题日趋严重，牵引部经常发生各种故障，如减速齿轮异常磨损、轴的疲劳断裂等[1-2]。牵引传动系统性能的优劣直接决定了采煤机的工作效率和可靠性。国内外学者对采煤机牵引振动系统及其扭振系统振动问题做了大量研究，其中，传递矩阵法是进行多圆盘系统扭振分析的有效方法之一[3-6]。利用传递矩阵法研究扭振问题的关键是轴系模型的建立。针对不同的研究目的，国内外学者建立了许多扭振模型，常用的模型主要有分布参数模型和集中质量模型两种[7-9]。在传统轴系动力学模型中，使用的往往是将轴系分成很多质量块的集中质量模型，这种模型存在一定局限性，只有在轮盘转动惯量远远大于轴自身转动惯量时才准确[10-12]。对于采煤机牵引系统来说，轴的转动惯量往往较大，与传统的集中质量模型并不完全适应。笔者将轴的分布质量计入整个扭振系统，以其提高扭振分析的准确性，以解决现有分析精度不足的问题，在得到扭振系统基本振型后，使用降梯度算法对扭振系统进行优化，解决系统弹性势能分布不均问题。

1 牵引部扭振模型

1.1 等效扭振模型

采煤机牵引系统中，轴的转动惯量往往较大，有必要将轴的分布质量计入整个扭振系统，提高扭振分析的准确性[13]。建立扭振力学模型和数学模型时，假设相啮合的两齿轮中心距不变，只做扭转运动；齿轮为理想刚性体；忽略轴承和轴的弹性变形；忽略系统间隙和轮齿间摩擦力。图1所示为扭振系统力学模型。

按照能量守恒的原则，将输入端电机作为等效构件，将牵引部传动系统的扭振模型按照能量守恒的原则转化为一等效扭振系统。不考虑轴的弯曲变形及轴的质量，以某型号采煤机为例，转化后，各轴转速n1～n6分别为1 470.0、474.9、224.6、42.4、9.0、12.6 r/min,轴段长度L1～L6分别为110.0、80.0、203.5、209.5、488.0和150.0 mm。

图1 采煤机牵引部传动系统扭振模型的等效转换Fig.1 Euivalent transfor of mode torsional vibration of transmission system of shearer traction

1.2 转动惯量的等效换算

利用动能不变原则，将行星轮系等效为一惯性圆盘[14]。该行星减速器为二级行星减速机构，一级传动有3个太阳轮，二级传动有4个太阳轮，将行星轮转动惯量等效到输出端行星架上，有

式中：ω、ωT、ωX——行星架、太阳轮、行星轮角速度，r/min；

J、JT、JX——行星架、太阳轮、行星轮转动惯量，kg·m2；

d——行星轮直径，mm；

n——行星轮个数。

经计算，两级行星减速机构的等效转动惯量依次为86.34和362.35kg·m2。

1.3 变截面轴的扭转刚度

采煤机牵引传动系统中，轴的结构都较为复杂，多为阶梯轴、花键轴或带有键槽的轴，不同结构截面处轴的极惯性矩不同，用通常求轴系扭转刚度的常规方法并不准确[15]。采用有限差分法，对圣维南扭转应力函数求解[16]，得到带有键槽的轴和花键轴的扭转刚度k为

k=GKD4/8l，

式中：G——剪切弹性模量，GPa；

K——力矩系数；

D——轴的直径，mm。

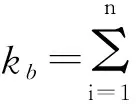
1.4 扭振系统分布质量的数学模型

牵引部扭振系统内任一截面位置包含两个变量：扭转角θ和扭矩M。采用分布质量模型将齿轮简化为一惯性圆盘，其质量集中在几何中心，将轴看作具有连续质量和刚度的弹簧，假设其阻尼为0。如图2所示，设扭振系统中的第i轴段总长为Li，在位置li处，取一小段dli作为分析对象，由达朗贝原理，轴段任意位置扭转角θ(li)的静态方程和动态方程分别为[17]

(1)

(2)

整理，得

(3)

式中：Ipi——该轴段的极惯性矩，mm4；

ρ——轴段的密度，kg/mm3。

图2 扭振系统轴段分析Fig.2 Torsional vibration analysis system of shaft segment

将轴段分布质量计及扭振系统，原扭振系统中的轴单元传递矩阵将发生变化，用HLi表示轴段分布质量下扭振系统的轴单元传递矩阵，则考虑轴的分布质量模型下，牵引扭振系统数学模型为

(4)

2 牵引部扭振系统传递矩阵

轴段任意位置的扭转角为

(5)

c1、c2——系数。

设轴段i左侧扭矩为Mi0，右侧扭矩为ML，有

(6)

(7)

因此，轴段两端的轴单元传递矩阵HMi为

(8)

将式(8)替换第i个圆盘的传递矩阵HKi，代入集中质量模型下扭振系统总传递矩阵，即式(5)，得到轴段分布质量模型下单元传递矩阵为

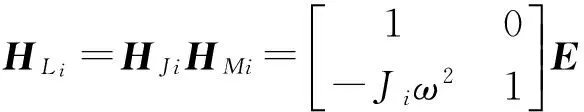
(9)

扭振系统总传递矩阵为

(10)

3 牵引部扭振系统振动特性

3.1 扭振系统固有频率

由式(6)、(8)及(10)可知，采煤机牵引扭振系统振动方程为

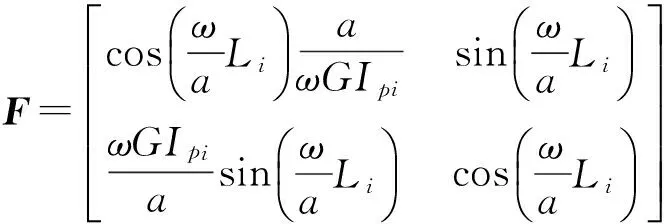
(11)

为了方便求解频率和振型，将HLi中的三角函数在实域展开，由于正弦、余弦函数在实域收敛，将其展开为ω的泰勒级数(取n=3)[18]，有

(12)

(13)

将式(12)、(13)代入式(10)中，得到简化后的HLi，即

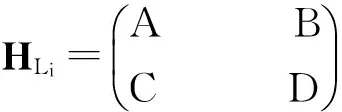
(14)

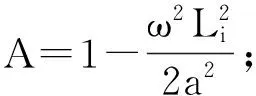
由边界条件知，电机轴端，其扭转角为0，输出轴端，其扭矩即为牵引负载扭矩，则有f22=0，求解该式，得到牵引扭振系统固有频率值ω1～ω6分别为8.52、18.49、65.44、349.69、11 236.00、42 025.00Hz。

3.2 扭振系统振动模态

假设等效扭振系统最左端处扭转角为1，计算得到前两阶固有频率所对应的振幅比，得到一阶主振型如图3a和二阶主振型如图3b。

a 一阶主振型

b 二阶主振型

由图3可知，各轴段扭转变形较为均匀，但由于各轴段等效扭转刚度相差较大，扭振系统中各轴的弹性势能分布并不均匀，用Ei表示第i段轴的弹性势能，则

式中：θi——第i段轴右侧的扭转角，rad；

ki——第i段轴的扭转刚度，kN·m。

计算得到两种模态下系统势能基本相当，一阶模态下系统末端扭转振幅较大，且由前面实验结果可知，截割阻力频率主要集中在0～15 Hz之间，因此，一阶模态为系统危险模态。一阶模态下各轴段弹性势能在整个系统中的分布如图4所示。由图4可知，系统势能分布极不均匀，5、6轴段的弹性势能较高，对应牵引系统中的行星减速器输出轴和行走轮轴。为使扭振系统具有最佳动态特性，要保证各轴段弹性势能分布尽量均匀。因此，需要对扭振系统中行星减速器输出轴和行走轮轴扭转刚度进行优化。

图4 各轴段弹性势能分布Fig.4 Segment elastic potential energy distribution histogram for each axis

4 牵引部扭振系统参数优化

4.1 优化建模

一般的优化问题可表示为

minf(x),

s.t.gi(x)≤0；i=1,2,…,m，hj(x)=0,j=m+1,m+2,…,p;

式中：f(x)、gi(x)、hj(x)——n元函数；

f(x)——目标函数；

gi(x)——不等式约束条件；

hj(x)——等式约束条件；

x——设计变量。

以行星减速器输出轴和行走轮轴扭转刚度作为优化参数，设其分别为k5b、k6b，行星减速器输出轴通过联轴器与行走机构相连，因此，其扭转刚度范围可取得大一些，设其值在0.5k5～2k5，行走轮轴通过内花键与行走轮相连接，其扭转刚度范围不宜过大，设其值在0.8k6～1.5k6[19]。

设优化后系统各轴段扭转角为θi，各轴扭转刚度为kib，以系统中各弹性轴段势能均有所降低，且分布最均匀作为优化目标，建立如下目标函数：

s.t.gi(x)=θi-φi≤0,i=1,2,…,6; hj(x)=kj-kjb=0,j=1,2,3,4;k5b=0.5k5～2k5,k6b=0.8k6～1.5k6。

(15)

4.2 优化算法及结果分析

降梯度算法是迭代算法中的一种，能够有效解决一般的非线性优化问题[20]。设xu∈n是第u轮迭代点，而xu+1∈n是第u+1轮迭代点，记

xu+1=xu+λupu,

式中：λu∈n——步长；

pu∈n——搜索方向。

在λu和pu确定之后，由xu∈n就可以确定xu+1∈n。

在ADAMS中建立图2所示系统的等效扭振模型，并将各轴柔性化，得到分布质量仿真模型。利用ADAMS软件中优化分析工具，使用上述算法对优化目标函数进行计算，优化后，k5b=0.81k5，k6b=0.74k6，说明，提高行星轮系输出轴刚度及行走轮轴刚度均有利于提高系统的动态特性。优化后的扭振系统各轴段弹性势能分布如图5所示。

图5 优化后各轴段弹性势能分布直方图Fig.5 Optimized paragraph elastic potential energy distribution histogram for each axis

对比图4与图5，优化结果表明，提高行星轮系输出轴刚度及行走轮轴刚度均有利于提高系统的动态特性，优化后，系统弹性势能不均匀性由40%降低到10%，不但各轴扭转变形有所降低，且各轴段弹性势能分布均匀程度明显提高。

5 结 论

(1)根据采煤机牵引传动系统的结构特点，使用集中质量模型与连续质量模型相结合的方法，建立采煤机牵引传动扭振系统力学模型，采用等效构建法对模型进行等效处理，得到扭振系统的等效扭振模型。

(2)依据牵引部扭振系统中轴系的连续质量特征，推导了扭振系统的传递矩阵，假设系统一阶模态下固有频率为ω=100 rad/s，Li=0.5 m，经计算，当n=2时，传递矩阵系数项的相对误差er(sin)≤0.116 1%，er(cos)≤0.000 06%，提高了扭振分析的精度。该矩阵在纯扭系统中具有通用性，可作为其他扭振系统振动分析的参考。

(3)建立采煤机牵引传动系统动力学模型，计算扭振系统的固有频率和一阶振动模态，结果表明，牵引传动系统弹性势能分布极不均匀，以系统弹性势能均匀分布作为优化目标，对扭振系统进行参数优化。优化后，系统弹性势能分布均匀性明显提高，优化后的行星轮系输出轴刚度k5b=0.81k5，行走轮轴刚度k6b=0.74k6，优化结果表明，降低行星轮系输出轴刚度及行走轮轴刚度均有利于提高系统的动态特性。

[1] 刘春生，任春平，李德根.修正离散正则化算法的截割煤岩载荷谱的重构与推演[J]．煤炭学报，2014(5): 981-986．

[2] 刘春生，田 操，李孝宇．大采高采煤机双列四驱动自适应调姿牵引方式研究[J]．煤炭科学技术，2016，44(10): 125-130．

[3] 杨海根，芮筱亭，刘怡昕，等.多体系统传递矩阵法分布式并行计算研究[J].振动工程学报，2014，27(1): 9-15.

[4] 孙世向,夏 季.考虑连续质量的扭振系统的传递矩阵分析[J].西南科技大学学报，2003,18(1)： 23-27.

[5] 朱自冰,朱如鹏,鲍和云.直升机尾传动系统扭转振动建模与特性[J].航空动力学报,2013(2): 92-99.

[6] 许得水,杜敬涛,李文达,等.任意边界条件弹性杆结构扭转振动特性分析[J].振动与冲击,2017(1): 161-166.

[7] 王 枫,陈 征,李 花.采用多体动力学的压缩机曲轴结构优化研究[J].西安交通大学学报，2017(3)： 1-6.

[8] Zhang Dan,Hu Shenghai,Liu Chunsheng,et al.Modeling and kinematics simulation of shearer’s travelling mechanism based on virtual prototyping technology[J].Advanced Materials Research,2013(3): 47-51.

[9] 时培明,夏克伟,刘 彬,等.含间隙多自由度轧机传动系统非线性扭振动力特性[J].机械工程学报,2012(1): 57-64.

[10] 王小莉,上官文斌,张少飞,等.发动机前端附件驱动系统-曲轴扭振系统耦合建模与曲轴扭振分析[J].振动工程学报,2011(5): 505-513.

[11] 唐进元,周 炜,陈思雨.齿轮传动啮合接触冲击分析[J].机械工程学报,2011,47(7)： 22-30.

[12] 李铁军.采煤机牵引部传动系统动态特性研究[D].太原： 太原理工大学，2005.

[13] 韩东颖,时培明,赵东伟.板带轧机机电传动系统参激非线性扭振鲁棒控制研究[J].振动与冲击,2016(12): 1-6.

[14] 陈志勇,毛 阳,史文库，等.基于双质量飞轮的启停工况传动系扭振研究[J].北京理工大学学报,2016(1): 42-47.

[15] 李建如.扭转梁扭转刚度的理论计算方法研究[J].机械强度,2015(2): 322-327.

[16] 吕 勇,李月强,陈青山,等.精密谐波齿轮柔轮扭转刚度测试与分析[J].机械传动,2013(12): 101-104.

[17] 刘春生,鲁士铂,张艳军,等.冲击载荷下不同有效长度扭矩轴的扭转特性[J].黑龙江科技大学学报,2014,24(2): 251-255.

[18] Zhang Dan,Hu Shenghai,Liu Chunsheng.Elastic model of shearer walking mechanism and traction characteristics[J].Joural of Applied Mathematics and Statistics,2013,51(12): 442-453.

[19] 张 丹，田 操，孙月华．销轨弯曲角对采煤机行走机构动力学特性的影响[J]．黑龙江科技大学学报，2014，24(3): 262-266.

[20] 车向前,张欣欣,边 莉.利用组合型交叉熵实现多处理机调度的算法[J].黑龙江科技大学学报,2016,26(3): 323-326.

(编辑 晁晓筠 校对 李德根)

Dynamic characteristics and optimization of shearer haulage section torsional vibration system based on distribution quality model

ZhangDan,LiuChunsheng,WangAifang,RenChunping

(School of Mechanical Engineering,Heilongjiang University of Science & Technology,Harbin 150022,China)

This paper is aimed at a solution to shearer haulage unit torsional vibration due to a variety of failures.The study using the equivalent component method consists of establishing a traction drive system of shearer torsional vibration analysis model of the equivalent,shaft section distribution quality torsional vibration mathematical model; calculating the vibration characteristics of torsional vibration system of shearer traction under the distributed mass model; developing the natural frequency and vibration mode of the system; and optimizing the parameters of the torsional vibration system by taking the distribution of potential energy distribution in each elastic axis as the optimization target,using The elastic energy potential variance as the objective function ,and using the gradient algorithm.The results show that the matrix versatile in the system of pure torsion system may work as a solution to the insufficient accuracy of torsional vibration analysis under concentrated parameter model; the optimization allows the elastic potential energy of the output shaft and the running axle of the planetary reducer to be reduced from 40%,41% to 23% and 22% respectively,contributing to a significant improvement in the elastic potential uniformity and the dynamic characteristics of the system are improved.The study may provide a theoretical basis for determining the parameters of the drive system of the shearer and the improvement of the torsional dynamic characteristics.

shearer; traction drive system; distribution quality model; transfer matrix; torsional vibration model; parameter optimization

2017-02-10

哈尔滨市科技局创新人才项目(2015RAQXJ017)

张 丹(1982- )，女，黑龙江省哈尔滨人，副教授，博士，研究方向：多刚体动力学仿真，E-mail：bishe_2006@163.com。

10.3969/j.issn.2095-7262.2017.02.003

TD421.6

2095-7262(2017)02-0109-05

A