小学数学作业错例分析与资源化利用摭淡

何琼瑛

学生作业中的错例是普遍存在的，仔细分析错例产生的原因却发现其中存在差异。从实践中我们发现，很多学生的错例是我们教师始料未及的，有些想法甚至很“天真”。因此，教师遇到作业中的错误，不能简单地概括为“粗心”“没看清题目”等，而要与学生沟通，架设让学生走出错误思维的阶梯。

一、错例归类整理及成因分析

错例分析应基于学生的基础与现状、学习心理和非智力因素三方面展开，链接教师的课堂教学行为和教材编排合理性。错例分析也应从根本上寻找错例产生的缘由，挖掘错例中蕴涵的教学价值，为教师教学提供建议，以减少学生错例的发生概率。我们在实践中总结、提炼了八大错例及相应的教学策略（案例选自人教版教材及配套练习）。

1.知识性错误——对照矫正

在六年级下学期学习完“正反比例的意义”后，学生对于正反比例的判断存在很大的困难，尤其若题目涉及圆形的周长、面积和体积则更难于区分。

如：圆的周长和它的直径（ ）；圆的面积和它的半径（）。

六年级备课组通过学生错例分析后一致认为：学生存在此类知识性错误的原因是学生初涉正反比例，对于抽象的无数据支撑的图形类判断缺乏有效的解答策略。提出增加一课时专项训练、对照矫正的教学建议，设计以下主要教学环节：

（1）讨论：圆的周长和它的直径成（ ）比例，说明理由。

（2）引导学生小结方法，可以利用假设法，列表解答，观察两个对应量的商或积是否一定。

（3）讨论：圆的（ ）和它的（ ），（ ）比例，说明理由。

（4）引导归纳有关圆的正反比例关系。

（5）独立研究：__（图形）的__和__，（ ）比例。

2.方法性错误——重点矫正

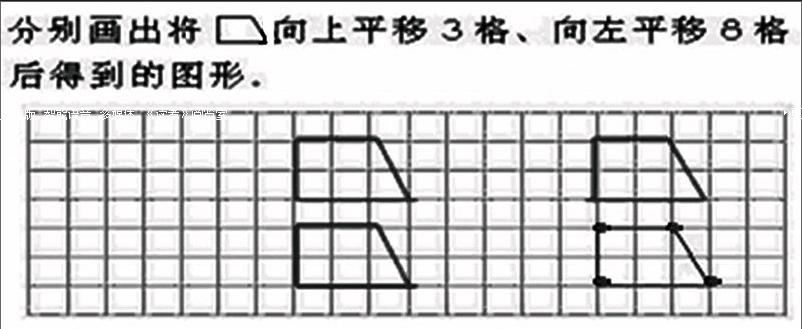
二年级下册教科书43页有这么一道练习题。

一教师统计了授课班级，并结合年级其他班的答题情况，反映有大部分学生无法正确理解中“分别”一词。认为题目的要求就是“画出将图形先向上平移3格，再向左平移8格后得到的图形”。该教师认为：学生是混淆了“先A再B”与“分别A，B”两种题型，产生混淆的原因是学生语言理解能力发展不完善。提出了以下矫正建议：

（1）在课堂教学设计中增加两种题型的对比，注重学生语言表达能力的训练。

（2）教学时设计提问：什么是“分别”？把“分别”一词去掉该怎么说？

（3）类似“分别”、“各”等字词，往往“隐蔽”在语句中，要善于发现、更要善于去掉。

3.习惯性错误——变式矫正

一年级上册“10以内加减法”单元，配套《课堂作业本》第36页第4题。

一教师统计发现本题错误率高达83%，认为学生受“熟题”的干扰而发生“习惯性错误”。学生在学习中，通过听老师讲、做练习等形式，积累了一定量的“经验题”，学生一旦遇到类似问题，便不假思索，以偏概全地分析问题，按原来形成的思路解答和得出答案。该教师提出以下教学建议：

（1）变式矫正，防止负迁移

根据学生的认知水平，选择具有针对性的题目，组织学生进行观察与思考。

-2 -3 -1 +6

8→口→口→口→口

8-2=口-3=口+1=口+6=口

（2）巧用比喻，杜绝负迁移

师生共同为题目起名字，把第1题命名为“算式接龙”，把第2题命名为“算式天平”。

4.普遍性错误——集中矫正

一年级第2册配套《课堂作业本》第18页上有一道题：

画一画，数一数。墙上缺了（）块砖。

图形本来是很直观的，但利用它的直观特点解题时，要发现其中蕴含的规律就不是简单能画出来的。教师提出教学建议：

（1）解答方法：截取的长度相等，每层砖头数目均为7块；每层缺少的砖块=7一已知的砖块；计算得出每层缺少的砖头数，总共缺少的块数。

（2）根据计算得数画出直观图，重点研究画的规律。

（3）几何直观，通过画图的方式来理解；逻辑思考，通过数形结合的方式来理解。

5.结构性错误——完善认知

五年级学生在学习方程单元后，遇到诸如未知数是减数、除数时，利用等式的性质解答就比较麻烦。教科书为了避免这个“麻烦”，从教材上删除了此类方程，但在方程的实际应用中，是无法避免的，如用方程解答：

一堆煤炭0.8吨，用了两天后，还剩下0.5吨。平均每天用多少吨？（0.8-2x=0.5）

学生对于两种解法有各自的想法：

解法一：0.8-2x=0.5

0.8-2x+0.8=0.5+0.8（两边同时加上0.8，就把左边的0.8去掉了）

2x=1.3

2x÷2=1.3÷2

x=0.65

解法二：0.8-2x=0.5

2x=0.8-0.5（一共0.8吨，最后剩下0.5吨，所以两天是用0.3吨）

2x=0.3

2x÷2=0.3÷2

x=0.15

教师在诊断分析学生的想法后，提出以下观点：

（1）如果避免未知数是减数、除数的方程，对于学生的认知结构是不完整的。

（2）学生的解法二给教学这类方程提供了思路，四则混合运算顺序的教学可以与情境结合，方程何尝不可，先结合情境研究解法，再总结解法、举一反三。

（3）完善学生的认知结构，才更有利于学生掌握知识之间的逻辑关系。

6.意料错误——设计矫正

六年级下册配套《作业本》第42页有这样一题：为庆祝元旦，三（1）班同学做小紅旗（如图）。现在有一张长1.4米，宽0.9米的长方形卡纸，最多可以做这样的小红旗多少面？

学生可能有两种解答方法：

方法一：1.4米=14分米，0.9米=9分米

（14×9）÷（2×2÷2）=63（面）

方法：1.4米=14分米，0.9米=9分米

14÷2=7（面）9÷2=4（面）7×4×2=56（面）

教师在访谈后发现：学生已经较好地掌握了图形分割问题的解答方法，能说清楚其中的缘由，能将等腰直角三角形转化成正方形再解答。但，正确答案是60面（如下图），此类错例的产生是教师预料之中的，标准答案的解法需要利用“勾股定理”计算，而六年级的学生根本没有这个基础，本题出题不当。

重新定位本题的功能后，六年级备课组提出以下教学建议：

（1）本题改为思维拓展，不要求人人掌握，标准答案可供学生参考。

（2）組织学生讨论两种方法，各自称述理由，重点掌握。

（3）提示换角度思考：四个等腰直角三角形也能拼成正方形，了解画法。

（4）画一画、量一量、算一算。

二、错例资源化利用

在研究过程中，我们感到这些错例资源的重要作用与对现实教学的重大指导意义，如果只是将其收集、整理，那么对错例的利用是不充分的。如何将这些分门别类，具有年级特点的错例资源化呢？带着这样的思考，我们进行了探索：

1.错例资源的传承制

教师记载的错例绝不能用完就扔，可成为档案资料。新学年任教教师传承上届教师记录《错例记载本》，作为二度备课的主要参考资料，在备课过程中继承、分析记载的错例。这样的传承方式首先能使教师的二度备课更有方向性。学生在哪些地方容易出错，学生对这类问题的认识起点在哪里……这些思考都能从上届教师的记载与分析中得到一定的科学回答，同时也避免了重复、低效劳动，让教师有更多的精力继续深入地看待错例，进行补充，使得我们的错例资源更加完整。

2.错例资源的网络化

随着网络的不断进步，网络资源共享错例成为了可能。教研组可将教师撰写的错例分析进行整理，统一上传学校网站FTP和教研组文件，进行网络的共享与合作，让错例资源在分享中被反思、被质疑、被充实，从而使之更合理。

3.练习题库建设

我们建立了人教版全十二册练习题库。题库的建设基于对错例研究的成果，基于教师对学生的起点进行科学定位，基于对教学内容重难点的有效把握，将练习有层次、有实效地排布。教师执教时可以自主地选择适合本班学生的题目，进行针对性的练习；学生、家长也可以利用班级QQ群资源共享，有针对性地进预习、复习。