浅谈数学创造性思维及其培养

林淑娟

（福建省龙海市实验中学）

摘 要：在课堂教学中，教师要善于激发学生的学习潜能，多引导学生动手、动脑，充分发挥学生的观察力、想象力、思维力、运算能力等，从而促进学生数学创造性思维能力的发展与提高。

关键词：创造性思维；观察力；想象力；变式训练

社会在发展，要求老师不断更新教育观念，因此，我认为应当把数学思考的能力和创新精神作为我们教学的目标之一，注重培养学生的创新与实践能力。

我们的思维具有灵活性和独创性，这在数学应用中显得特别重要。例如：水池有甲、乙、丙、丁四根进水管，甲、乙、丙三管同时打开，12分钟可注满水池；乙、丙、丁三管同时打开，15分钟可注满水池；甲、丁两管同时打开，20分钟可注满水池。如果四管同时打开，需要多少时间可注满水池？学生解题时基本上是按常规做法，先设未知数，然后列出方程组解答。但有个学生这样分析：两个甲管，两个乙管，两个丙管，两个丁管同时打开一分钟，可注满水池的12分之1加15分之1加20分之1，即5分之1，所以，甲、乙、丙、丁四管同时打开一分钟可注满水池的10分之1。因此，注满只需10分钟。这种解法打破了常规的思维，充分应用题中的隐含条件，使解题过程简化，是创造性思维的结果。

在数学教学过程中怎样培养学生的创造性思维呢？首先，教师要注重发展学生的观察力，创造是从观察开始的。一方面，在数学教学过程中，精心创设问题情境，多引导学生仔细观察，从而发现问题，分析、解决问题。设置具有一定思考价值的问题，能提高学生的创造能力，并能激起学生强烈的求知欲望。在教学“二元一次方程组”时，可以设这样的问题，某纸品加工厂要制作两种无盖的长方体小盒，利用边角料裁出正方形和长方形两种纸片，正方形和长方形有一条边长相等，都是5厘米，现将150张正方形硬纸片和300张长方形硬纸片全部用于制作这两种小盒，请猜猜，一共可以做多少个小盒？学生通过思考，把纸片进行不同的组合，提出了想法：用四块长方形纸片加一块正方形纸片，可组成一个长方体盒子，用五块正方形纸片可组成一个正方体盒子，即300÷4=75，（150-75）÷5=15，所以一共可以做90个小盒。教师对学生的结果进行肯定和鼓励，接着告诉学生，学好了今天的內容——二元一次方程组，同学就可以通过列方程组的方式来解决这个问题。像这样，让学生带着问题学习，更能唤起学生的学习兴趣。另一方面，鼓励学生质疑，强化学生的问题意识。例如，在学习正多边形的有关知识时，我们要用多边形镶嵌平面，可以提问：用正三角形能铺满平面吗？因为正三角形的每个内角为60度，6个60度可以围成一个周角，所以，用正三角形能铺满平面。接着，有些学生就提出了若用任意三角形或正五边形等其他图形能铺满平面吗？我们利用学生自己提出的问题，让学生互相讨论，从而得出结论，最后，老师再进行小结：当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个360度周角时，就能铺满成一个既不留空隙又不互相重叠的平面图形。

其次，注意对学生想象力的培养，加强动手操作培养学生的创新能力。想象在数学创造中起着关键作用，想象是思维探索的翅膀。例如：用给定的图形（两个三角形，两个圆形，两条平行线段）为构件，尽可能地画出构思独特且有意义的图形，并写上一两句贴切的解说词。学生对这种题目较感兴趣，就是平常数学基础很差的学生，他们也能认真地画。学生画出了各种各样的图形，如图所示：

两盏电灯 好朋友 两条金鱼 一副羽毛球拍 一副吊环

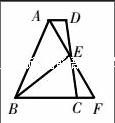
最后，要注重学生的探索过程。在组织教学过程中，加强变式训练。在训练中展开一题多变，把一道题发散成一系列题，形成题组。通过变式训练，锻炼学生灵活的头脑，防止学生在理解知识中的思维定势，提高学生的探究能力。例如：（如图）已知梯形ABCD中，AD∥BC，AD+BC=AB，E为CD的中点，试说明AE⊥BE。

证明：将△ADE绕点E旋转180度至△FCE，（DE=CE），

则AE=FE，AD=FC，∠ADE=∠FCE。

因为AD∥BC，∠D+∠BCD=180度

所以∠FCE+∠BCD=180度，即点B、C、F三点共线。

因为AD+BC=AB，所以CF+BC=BF=AB。因此，BE⊥AF，即AE⊥BE。

这道题我们是通过旋转的方法加以证明的，做完这道题，我们要特别注意这个典型数量特征“AD+BC=AB”，它常出现在一些题目中。

总之，人贵在创造，让我们共同从课堂做起。鼓励学生大胆创新与实践，使每个学生都得到充分的发展，从而加快学生创造性思维能力的形成和提高。

参考文献：

吴炯圻，林培榕.数学思想方法：创新与应用能力的培养[M].厦门大学出版社，2009.

编辑 谢尾合