授之以渔策略的案例分析

朱梅芳

[摘要]数学教育不仅是传授数学知识、技能和能力，更重要的是培养数学思维和自主学习的能力。《四种命题及其关系》这节课有着几个特点：一是复习旧知，渗透类比思想；二是巧妙引导，探究构建新知；三是尊重学生，体现人文关怀；四是及时反思，构建高效课堂。

[关键词]案例分析 自主 合作 探究

新课标下教师用新的理念去教学，新课标倡导自主、合作、探究学习，注重学习的过程性，通过观察、比较、类比等活动发现对象的某些特征与其它对象的区别与联系.下面一堂比武课《四种命题及其关系》，真实的反映了在教学中启发引导学生积极探索，激发学生自主学习数学，是一堂授之以渔策略的教学案例示范。

[案例描述]：四種命题及其关系教学设计

一、教学目标

1.知识与技能

了解原命题、逆命题、否命题、逆否命题这四种命题的概念，掌握四种命题的形式和四种命题间的相互关系，会用等价命题判断四种命题的真假。

2.过程与方法

多举命题的例子并写出四种命题，培养学生发现问题、提出问题、分析问题、有创造性解决问题的能力。

3.情感、态度价值观

通过学生的参与，培养他们的辨析能力，以及分析问题和解决问题的能力。

二、教学重点

四种命题、四种命题的真假判断及其关系。

三、教学难点

四种命题的书写，四种命题的真假判断。

四、教学过程

1.复习引入

（1）复习：什么是命题？命题的分类及构成

（2）预习：四种命题的形式（阅读课本第4页至第8页）

2.新课讲授

[探究一]下列四个命题中，命题（1）的条件和结论与命题（2）（3）（4）的条件和结论之间分别有什么关系？

①若两个三角形全等，则它们的面积相等；

②若两个三角形的面积相等，则它们全等；

③若两个三角形不全等，则它们的面积不相等；

④若两个三角形的面积不相等，则它们不全等；

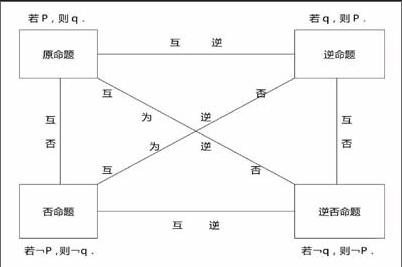
定义1：一般地，对于两个命题，如果一个命题的条件和结论分别是另一个命题的结论和条件，那么我们把这样的两个命题叫做互逆命题.其中一个命题叫做原命题，另一个命题叫做原命题的逆命题。

定义2：一般地，对于两个命题，如果一个命题的条件和结论恰好是另一个命题的条件的否定和结论的否定，那么我们把这样的两个命题叫做互否命题。其中一个命题叫做原命题，另一个命题叫做原命题的否命题。

定义3：一般地，对于两个命题，如果一个命题的条件和结论恰好是另一个命题的结论的否定和条件的否定，那么我们把这样的两个命题叫做互为逆否命题。其中一个命题叫做原命题，另一个命题叫做原命题的逆否命题。

四种命题的形式：

若原命题为：若P，则q；则逆命题：若q，则P.

否命题：若P，则，q；逆否命题：若，q，则，P.

例1写出下列命题的逆命题、否命题、逆否命题并判断它们的真假：

（1）若一个函数是偶函数，则这个函数的图像关于y轴对称；

（2）若一个整数的末位数字是0，则这个整数能被5整除；

（3）若两个三角形相似，则这两个三角形的面积相等；

（4）若x2=1，则x=1；

[探究二]你能说出[探究一]的四个命题中任意两个命题的条件和结论之间的关系吗？

[探究三]原命题的真假与其它三种命题的真假有什么关系？

（1）两个命题互为逆否命题，它们有相同的真假性；

（2）两个命题为互逆命题或互否命题，它们的真假性没有关系。

例2原命题：若|x|=x，则x≥0，那么其逆命题、否命题和逆否命题分别是什么？这些命题的真假如何？

练习：

1.（A级）判断下列命题的真假：

（1）命题“若x+y=0，则x、y互为相反数”的逆命题。

（2）命题“若ab=0，则b=0”的逆否命题。

2.（B级）写出命题“若x2-3x+2=0，则x=2”的逆命题、否命题和逆否命题并判断真假。

3.课堂小结

（1）逆命题、否命题与逆否命题的概念；

（2）两个命题互为逆否命题，他们有相同的真假陛；

（3）两个命题为互逆命题或互否命题，他们的真假性没有关系；

（4）原命题与它的逆否命题等价；否命题与逆命题等价。

4.课后作业：课本P8第1、2、3题

[案例分析]：

《四种命题及其关系》这堂课在老师的精心设计下让学生的学习热情和潜能极大地激发出来，充满生机的课堂交流与探讨，围绕数学问题的思维碰撞，无不是学生学习主动性，能动性和创造性的表现，让我看到了在教育教学活动中，真正的学习是学生作为一个完整的生命体的方式参与投入。

一、回顾旧知，渗透类比思想

本节课教学设计，通过创造愉悦的情景，使学生了解逻辑在生活中的应用，引起学生的学习兴趣，在轻松欢快的气氛中探索问题，解决问题。

二、创设情境，探究构建新知

本节课的教学设计的核心部分就是四种命题及其关系的探究，而新课程理念下数学教学中，数学知识已经不是教学的全部内容了，如何在知识教学的同时培养学生的观察、探究、合作、归纳等方面的能力才是新课程改革的主导方向，这节课的教学设计在这一方面做了良好的尝试。

三、尊重学生，培养自主能力

重视评价、激励促发展。给学生提供相对复杂的问题，在探讨中使思维更严谨，视野更开阔。

四、反思教学，打造高效课堂

1.PPT课件与板书的结合恰到好处

课堂上，运用板演，相互交流，投影仪展示等方式，使课堂更加充满活力。多媒体课件始终代替不了板书的作用。

2.动态的效果与理性的思维结合相得益彰

动态直观的动画并不能直达数学的本质。我们可以通过动画来吸引学生的眼球，通过动画的直观来弱化难点，使得难以想象或难以表述清楚的内容直观呈现，然而没有数学思维的参与，并不能使学生透彻掌握。

3.学生自主学习与教师启发引导结合效果更佳

采用启发式教学，教师能根据具体的教学内容，引导学生开展有效的学习，体现动手实践、自主探索、合作交流等有效的学习方式，让学生自主学习。