特种摩托车悬架系统动力学仿真及遗传算法优化

朱 强，周良生，杨福威，王志翔

(1.军事交通学院 研究生管理大队，天津 300161； 2.军事交通运输研究所，天津 300161；3.中国北方车辆研究所，北京 100072； 4.北京理工大学 机械与车辆学院，北京 100081)



● 车辆工程 Vehicle Engineering

特种摩托车悬架系统动力学仿真及遗传算法优化

朱 强1，周良生2，杨福威3，王志翔4

(1.军事交通学院 研究生管理大队，天津 300161； 2.军事交通运输研究所，天津 300161；3.中国北方车辆研究所，北京 100072； 4.北京理工大学 机械与车辆学院，北京 100081)

为提高摩托车悬架系统的寿命和行驶安全性，采用遗传算法对悬架的弹簧刚度和减震器阻尼进行优化。遗传算法程序通过Matlab M文件进行编写，以车辆质心加速度、悬架动挠度和相对动载荷为待优化项，经过选择、交叉和变异，获得优良后代。结果表明：参数优化后，悬架动挠度减小了37%，车轮相对动载荷减小了22%。

摩托车双横臂悬架；Matlab；遗传算法

操纵稳定性是车辆的重要性能之一。设计一种用于特殊用途作业的全地形摩托车，将传统的潜望镜式前叉的前悬架结构，改为使用质量轻、结构强度高、操纵稳定性更好的双横臂结构。悬架参数在进行第一轮的工程计算后，需要进一步使用相应算法进行优化。响应面法和遗传算法是应用比较广泛的两种算法。

响应面法优化是试验设计与数理统计相结合的优化方法。王延克等[1]运用响应面法对汽车的悬架刚度和结构参数进行优化，简化了其与车辆性能指标之间的评价关系，并将这种复杂关系设计成了响应面模型。遗传算法优化早在1967年Bagley首次提出，经过不断发展，在车辆系统优化方面得到了广泛应用。Baumal等[2]提出了一种基于遗传算法的优化模型，优化后车身的垂向加速度均方根值减小了38%。李仲兴等[3]提出一种混合多目标系统的优化数学模型，采用多目标遗传算法NSGA-I来解全局最优解。

本文设计的摩托车要求质量轻、结构强度高，前悬架采用了双横臂式的结构[4]。前后车轮用轮毂电机驱动，在前轮上方加装转向电机，实现车轮的转向，同时为了增加转向可靠性，设计了手动转向和自动转向两种模式。

1 系统振动方程及仿真模型

1.1 整车模型的建立

假设除弹簧和减震器外，其他构件均为刚体，并忽略运动副处的摩擦，建立轮胎模型只有刚度没有阻尼[5]。

如果考虑双横臂摆角、减震器后倾角的实时变化对弹簧力、阻尼力的影响，这样建立的模型会十分复杂，并且得到的振动微分方程很难求解，不利于进行分析。所以必须将模型进行简化，成为只考虑垂向作用的振动系统，简化的模型如图1所示。

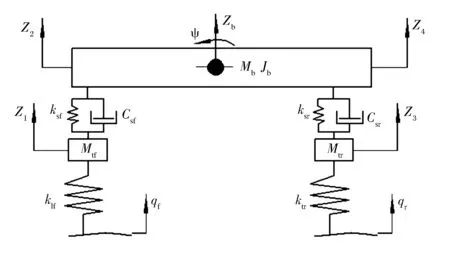
图1 摩托车四自由度简化振动模型

图中：ksf和ksr分别为前、后悬架垂直方向等效弹簧的总刚度；qf和qr分别为作用在前、后轮的路面激励；Csf和Csr分别为前、后悬架垂直方向减震器的阻尼，在进行模型简化之后，需要计算垂向方向的等效刚度和等效阻尼[6]。

1.2 前后悬架等效刚度和阻尼的计算

1.2.1 前悬架等效刚度和阻尼

图2 双横臂扭杆前悬架受力模型

车轮质心等效变形δl、等效受力F、前悬架垂直方向等效弹簧总刚度ksf分别为

(1)

(2)

(3)

减震器等效阻尼的计算和扭杆弹簧等效刚度的计算原理相同，也是利用力杠杆比和位移杠杆比进行计算，减震器等效阻尼计算式为

(4)

1.2.2 后悬架等效刚度和阻尼

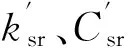
(5)

(6)

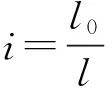
1.3 系统振动方程的建立

运用拉格朗日法进行求解。首先确定系统的动能Ek、势能Ep和耗散能Ed，计算式分别为

当俯仰角较小时，可以近似地认为

Z2=Zb-aφ

Z4=Zb+bφ

将以上各式带入拉格朗日方程，得到系统的运动微分方程为

ktf(qtf-Z1)=0

kf(Z1-Z2)=0

ktr(qtr-Z3)=0

ksr(Z3-Z4)=0

1．4 建立状态方程

2 路面激励及其不平度时域信号的生成与仿真分析

车辆振动的路面激励主要用路面功率谱密度来表示。功率谱密度的拟合表达式[7]为

(7)

式中：n为空间频率,是波长λ的倒数，m-1；n0为参考空间频率，n0= 0.1 m-1；Gq(n0)为参考空间频率下路面功率谱密度，m3；w为频率指数，是双对数坐标上斜线斜率，w=2。

路面不平度的时域模型的生成有多种方法，如滤波白噪声生成法、谐波叠加法、快速傅里叶逆变换生成法等[8]。本文采用滤波白噪声生成法。滤波白噪声法是将路面随机扰动抽象为一定条件的白噪声，然后经滤波器进行适当变换拟合出具有指定谱特征的随机过程[9]。系统的微分方程为

(8)

式中：w(t)为白噪声时域信号；q(t)为路面谱时域信号；n00为空间下截止频率，n00= 0.011 m-1。

前后轮白噪声输入关系为

ωf(t)=ωr(t+td)

在Matlab/Simulink中搭建仿真平台，使用高斯低通滤波器对有限带宽白噪声进行滤波，分别在C级路面和D级路面以5 m/s的车速进行仿真。将对应参数输出到状态空间，通过M文件进行编程，得到5个评价指标的时域和频域响应。通过计算得出质心加速度，前、后悬架动挠度和前、后车轮相对动载荷均方根值分别为[0.252 6，0.005 1，0.005 5，0.231 5，0.231 1]。

3 利用遗传算法进行悬架参数优化

遗传算法通过初始化产生种群，对种群成员进行选择、交叉和变异操作以获得优良后代，在工程上多用于参数寻优、结构优化等方面。这里的优化目标是使质心加速度、前后悬架动挠度、前后悬架相对动载荷尽可能小。由于待优化参数的单位不同，因此需要进行归一化处理后其倒数乘以相应的权重，各项相加得到目标函数[10]。

式中ω1～ω5为相应的权重系数，把前后悬架动挠度作为优先考虑的待优化项，根据算出的各项初始均方根值，取ω1=1.4，其余各项都为1。

这里，优化的参数只有前后悬架弹簧刚度和减震器阻尼[11]。设置初始种群为100，遗传的世代数上限为500次。选择方法采用轮盘赌，编码方法采用实数编码，相邻两元素间进行交叉。变异方法采用高斯变异和随机变异。子代的组成包括：使适应度函数取得最大值的2个父本、20个父本的高斯变异，20个父本的随机变异、58个父本的交叉。其中，每遗传10次，高斯变异产生的子代会减少一个。通过这种方法获得的子代既保存了父本优秀的基因，又防止出现局部最优解，能够最大限度地寻找到最优值。

车辆技术参数见表1，全为不需优化的参数。其中前、后轮轮胎刚度和质量相同，前悬架中两扭杆的刚度也相同。

表1 车辆技术参数

悬架原始参数和经过遗传算法优化后的车辆参数见表2。每一代种群的适应度函数最大值和平均值变化如图3所示。

表2 悬架原始及优化后参数

由图3可看出，适应度函数最大值变化较小，证明初始计算得到的悬架参数已接近优化值，所以优化的速度较慢。遗传到第10代左右，适应度函数基本已取到最大值，只是在很缓慢增加，算法的收敛速度较快。

经过遗传算法优化后得到的质心加速度，悬架动挠度和轮胎相对动载荷时域响应与未经优化的时域响应对比如图4—8所示。其中虚线代表未经参数优化的响应，实线代表经过优化后的响应。

图3 每一代种群的适应度函数最大值与平均值

图4 优化前后质心加速度时域响应对比

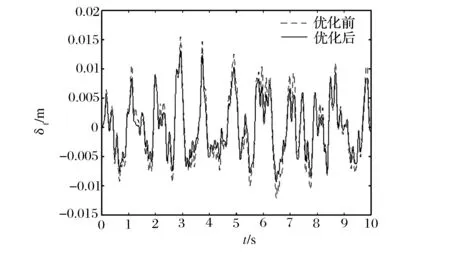
图5 优化前后前悬架动行程时域响应对比

图6 优化前后后悬架动行程时域响应对比

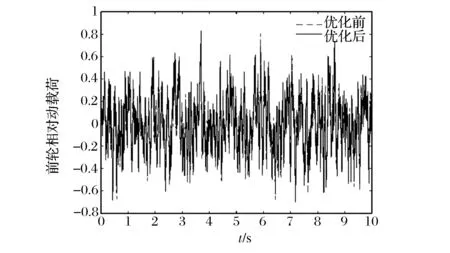
图7 优化前后前轮相对动载荷时域响应对比

图8 优化前后后轮相对动载荷时域响应对比

优化后，质心加速度、前、后悬架动挠度和前、后车轮相对动载荷均方根值分别为[0.255 8，0.003 2，0.002 8，0.178 5，0.177 3]。且由图4—8可看出，经过优化后，前后悬架动挠度和相对动载荷都有减小，但是质心加速度有所增加。不过增量较小，仍在可以接受的范围内。该遗传算法对于悬架优化具有较好的效果，能够提高悬架系统的使用寿命，也能一定程度上提高车辆的行驶安全性。遗传算法能够有效地运用到悬架参数优化当中。为避免出现局部最优解和负优化，对父代优良个体施加局部多次搜索算子，一旦搜索到优于父代的个体，立即替换。

4 结 论

(1)所设计的双横臂扭杆悬架摩托车，经过工程计算后得到悬架各部分的结构参数。利用拉格朗日法建立数学模型，在Matlab中建立Simulink模型，得到了车辆悬架系统的3个评价指标的时域响应和频域响应，结果具有一定的精确度。

(2)在用遗传算法进行参数优化时，需要确定设计变量、约束条件和目标函数，由于目标函数中的3个评价指标单位不一致，因此要进行归一化处理，每一项的权系数需要根据待优化模型的实际情况进行选择，权系数的选择对于算法的收敛速度和最终的优化速度具有重要影响。

(3)仿真结果显示，所设计的算法在第10次左右就已经收敛，收敛程度高，优化后悬架动挠度和相对动载荷有所减小，达到了优化的目标。

[1] 王延克,丁渭平,杜飞龙,等.基于响应面法的悬架结构改进及优化设计[J].机械科学与技术,2009(1):10-14.

[2] BAUMAL A E, MCPHEE J J, CALAMAI P H. Application of genetic algorithms to the design optimization of an active vehicle suspension system[J]. Compute Methods Appl. Mech. Egrg,1998(163): 87-94.

[3] 李仲兴,晋旋,江洪.基于NSGA-Ⅱ悬架参数优化设计[J].拖拉机与农用运输车,2010(1):29-31.

[4] 李新耀,张印,周良生,等.双横臂扭杆悬架的特性分析及设计计算[J].汽车工程,2003,25(1):15-19.

[5] 余志生.汽车理论[M].北京:机械工业出版社,1996:77-83.

[6] RAMON S. Kinematic design of double-wishbone suspension systems using a multiobjective optimisation approach[J]. Vehicle System Dynamics: International Journal of Vehicle Mechanics and Mobility, 2010, 48(7):158-164.

[7] 周长城.车辆悬架设计及理论[M].北京:北京大学出版社,2011:113-115.

[8] 冯金芝,李君,郑松林,等.车辆四轮随机输入模型研究[J].上海理工大学学报,2010,32(3):205-208.

[9] 尹志新,李端芳,唐萌,等.基于Matlab的时域路面不平度仿真研究[J].装备制造技术,2010(4):43-45.

[10] 孙靖,巩敦卫,季新芳.基于偏好方向的区间多目标交互进化算法[J].控制与决策,2013(4):542-546.

[11] 王南,张京军,高瑞贞.基于改进遗传算法多体模型的汽车悬架参数优化[J].辽宁工程技术大学学报,2007,26(3):435-437.

(编辑：张峰)

Dynamics Simulation and Genetic Algorithm Optimization of Suspension System of Special Motorcycle

ZHU Qiang1, ZHOU Liangsheng2, YANG Fuwei3, WANG Zhixiang4

(1.Postgraduate Training Brigade, Military Transportation University, Tianjin 300161, China;2.Institute of Military Transportation, Tianjin 300161, China;3.China North Vehicle Research Institute, Beijing 100072, China;4.School of Mechanical and vehicle, Beijing Institute of Technology, Beijing 100081, China)

To prolong lifespan and improve driving safety of motorcycle suspension system, the paper optimizes spring stiffness and damping of the suspension with genetic algorithm. By compiling M file of Matlab with genetic algorithm program and taking vehicle centroid acceleration, suspension dynamic deflection and relative dynamic load as optimization items, we obtained good offspring through selecting, overlapping and variation. The result shows that the suspension dynamic deflection reduced by 37% and the relative dynamic load of the wheel reduced by 22% after optimizing the parameters.

motorcycle double-wishbone suspension; Matlab; genetic algorithm

2016-10-09；

2016-11-29．

朱 强(1993—)，男，硕士研究生； 周良生(1965—)，男，博士，高级工程师，硕士研究生导师.

10.16807/j.cnki.12-1372/e.2017.04.012

U483

A

1674-2192(2017)04- 0048- 05