Linear Analysis of Obliquely Propagating Longitudinal Waves in Partially Spin Polarized Degenerate Magnetized Plasma
2017-05-09IqbalMurtazaandHussain
Z.Iqbal,G.Murtaza,and A.Hussain
1Salam Chair,Department of Physics,G.C.University Lahore,Katchery Road,Lahore 54000,Pakistan
2Department of Physics,Mirpur University of Science and Technology,Mirpur-10250(AJK),Pakistan
1 Introduction
Electrostatic waves are the basic collective phenomena in plasmas.In the spectrum of low frequency electrostatic waves,ion acoustic(IA)wave,ion cyclotron(IC)and lower hybrid(LH)wave have received considerable attention of physicists due to their potential applications in space and laboratory plasmas.LH waves propagate perpendicular to the external magnetic field.The resonant interaction of LH waves with electrons and ions is responsible for the transfer of energy between the two species,which leads to plasma heating or particle acceleration.Due to this characteristic,LH waves are important in both laboratory[1−2]and space plasma environments.[3−6]In a classical plasma the dispersion of LH waves has been derived[7]by including electromagnetic and warm plasma effects and it has been shown that this dispersion relation is more consistent with numerical results than the previously reported analytical dispersion relation.Moreover it is shown that when the ion magnetization effects become important,the continuous LH mode breaks up into a series of segments of ion Bernstein modes.The dispersion relations of the dust LH wave and dust LH surface wave have been derived using the quantum hydrodynamic model as in Refs.[8–9].It is found that the dispersion relations of these waves are signi ficantly affected by the quantum corrections.Using a quantum hydrodynamic model the excitations of LH wave have been investigated by injecting an electron beam in a semiconductor plasma[10]and found that an increase of the electron number density and streaming speed of the electron beam enhance the instability.Recently,Tripti and Prerana[11]studied the dispersion properties of LH wave in electron-ion degenerate plasma with Bohm potential and exchange correlation potential effects.They found that these effects signi ficantly modify the dispersion properties of LH wave.
The ion acoustic(IA)wave is one of the fundamental low frequency modes of plasma caused by density perturbations.These waves have been extensively studied in the solar wind and in various regions of the Earth’s magnetosphere.[12−14]The study of IA wave also gained its importance in quantum plasmas in order to understand the electrostatic wave propagation at the microscopic level.Electrostatic waves have also been studied in quantum plasma and it has been shown that,both the high frequency electron waves(Langmuir wave and upper-hybrid wave)and the low frequency ion acoustic and ion cyclotron waves can propagate when the plasmas are cold.[15]Using the quantum hydrodynamic(QHD)model,the effects of Bohm potential on the linear and nonlinear properties of the IA wave in an unmagnetized electron-ion plasma have been investigated in Ref.[16]and the quantum effects are found to modify the linear wave frequency.Hass and Mahmood[17−18]analyzed the linear and non linear IA waves in unmagnetized and magnetized quantum plasmas with arbitrary degeneracy of electrons.They found the dispersion relation of quantum IA wave in terms of generalized IA speed,valid for dilute and dense cases.
The electrostatic IC mode is another fundamental mode of a magnetized plasma.In a multi-ion species plasma,IC waves can have frequencies near their respective ion gyrofrequencies.These waves were first observed by D’Angelo and Motley in laboratory plasmas[19−20]and subsequently have been observed in space plasma by Mosier and Gurnett.[21]These waves are studied due to their importance in the heating of plasmas.[22]The excitation ofelectrostatic IC waves by an ion beam in a two-component collisionless or collisional plasma has been investigated in Refs.[23–24].Very recently,the coupling of electrostatic IC and IA waves has been examined in a three-component magnetized plasma consisting of electrons,protons and alpha particles and the results have been applied to the study of solar wind plasma.[25]
The QHD model was extended for spin-1/2 particles in Refs.[26–28].The derivation of QHD model for spin-1/2 particles was first presented by Kuzmenkov in 2001.Later,the so called spin-1/2 quantum plasmas in which the spin properties of electrons are taken into account,have received great attention due to the occurrence of some new wave phenomena.[29−37]Subsequently,the quantum kinetics for spin-1/2 quantum plasmas has been developed and applied to study the dispersion properties of various plasma waves.[31,38−43]
However,generalized QHD equations were obtained in Ref.[34]by considering the electrons with spin-up and spin-down as two different fluids.In the presence of ambient magnetic field,the equilibrium concentration of spinup and spin-down electrons are different(nu/=nd),which is responsible for the difference of Fermi pressures of the spin-up and spin-down electrons and the model is called separate spin evolution(SSE).The difference of Fermi pressures gives rise to a new type of longitudinal collective excitation in degenerate quantum plasmas.This excitation is called the spin-electron acoustic wave(SEAW).Oblique propagation of longitudinal waves with the SSEQHD equations in electron-ion(e-i)and(e-p-i)plasmas further gives birth to new type of spin-dependent longitudinal waves.[35−36]Non-linear analysis of these waves is given in Refs.[44–45]The new spin-dependent wave has also been found by applying the SSE-QHD equations to the two-dimensional electron gas in plane samples and nanotubes embedded in an external magnetic field in Refs.[46–47]Further,generalization of SSE-QHD equations by including the spin-orbit interaction(quantumrelativistic effects)has been presented in Ref.[48]This generalization is based upon the nonlinear Pauli equation by including Fermi spin current contribution in the spin evolution.It is demonstrated that the SEAW spectrum signi ficantly changes due to transverse part of the electric field and an extra shift in the extraordinary wave spectrum is observed due to the spin-orbit interaction.
From the above literature,one may notice that the low frequency electrostatic waves have been well studied in the classical and quantum plasma(without taking account of electron spin effects)regimes.The electron spin effects on the electrostatic wave have been investigated with the aid of SSE-QHD equations but in most of the investigations for electrostatic waves,the ion dynamic is ignored.In the present work we examine the electron spin effects on the linear low frequency obliquely propagating electrostatic(LH wave,IA wave,and IC wave)waves in degenerate magnetized plasma using the SSE-QHD equations and highlight the role of the new spin dependent wave on their spectra.
The article is organized in the following manner.In Sec.2,the dynamic equations are described to investigate the linear properties of longitudinal waves in partially spin polarized plasma and a general dispersion equation of obliquely propagating longitudinal waves is derived.In Sec.3,analytical and numerical analysis of waves under consideration is presented.Finally,the conclusion is described in Sec.4.
2 Governing Equations
We study the obliquely propagating low frequency electrostatic waves in collisionless electron-ion plasma embedded in an external magnetic fieldB0that is directed along thezdirection and the wave is taken to propagate in(x,z)plane at an angleθwithz-axis.The electrons and ions are considered to be degenerate and magnetized.The continuity and momentum equations for ions are given as

For governing the dynamics of electrons,we consider the SSE-QHD equations,which were recently developed in Refs.[34–35].In the SSE-QHD equations under the action of external magnetic field,each species with spin-up and spin-down are considered as a separate fluid.Therefore,the continuity equation with spin projection of each species is presented as

wheres=u,dfor the spin-up and spin-down state of particles,nesandvesare the concentration and velocity field of electrons being in the spin states,Tez=(γe/ħ)(BxSey−BySex)is the z-projection of spin torqueis:iu=2,id=1,with the spin density projectionsSexandSey,each describing the evolution of the spin-up and spindown states of particles andγe=−µB,µBis the Bohr magneton.Therefore,the functionsSexandSeydo not bear subindexesuandd.In this model,thez-projection of the spin densitySezis not an independent variable,it is a combination of concentrations i.e.,Sez=neu−ned.The momentum equation for electrons is given as



For the oblique propagation of longitudinal waves in electron-ion plasma,the required Maxewell’s equations can be written as

In order to study the linear response,we linearize Eqs.(1)–(2)and(5)–(8)by considering the first order perturbations only.Assuming sinusoidal perturbation ei(k·r−ωt),the resulting equations lead to dispersion equation



3 Analytical and Numerical Analysis of Low Frequency Longitudinal Waves
In this section,we explicitly derive the dispersion relations of waves under consideration from the dispersion Eq.(9).To obtain numerical results,we choose the plasma regime having equilibrium number densityn0e=1027cm−3,the electrons Fermi temperature corresponding to this density isTFe=(3π2n0e)2/3(ħ2/2mekB)=4.23×107K,for degenerate ions[34,41]TFi=2.30×104K,which means that our results are applicable in the plasma regimes having thermal temperatureT<TFi.Further,for the variation of spin polarizationηwe keep number density fixed and consider the variation of ambient magnetic fieldB0in the range from 1010G to 4×1011G.Our results can be applied to the degenerate astrophysical plasma environments.
3.1 Lower Hybrid Waves
In this section we are interested to study the dispersion properties of LH waves.In the first case,ions are unmagnetized and electrons are magnetized and the propagation is perpendicular to ambient magnetic field(θ=π/2).Applying LH wave conditionωci≪ω≪ωce,we obtain
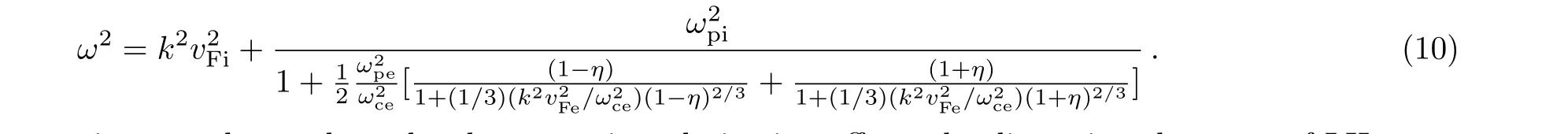
From the above equation,we observe how the electron spin polarization affects the dispersion character of LH wave.Here,it is important to mention that we have neglected the Bohm potential effects because the same has already been discussed quite a lot in the literature.If we consider the electrons as a single fluid and assumeω2pe≫ω2ce,we retrieve the results of LH wave discussed in Ref.[7].The dispersion relation(10)is plotted in Fig.1,which shows the effect of spin polarization on the frequency of wave.It is obvious from the graph that the frequency of LH waves decreases as we increase the spin polarization.The wave under consideration bears cyclotron character and one would expect the frequency of the wave to increase with magnetic field.Thus for fixed values of equilibrium number density,the spin polarizationηwould increase with magnetic field and the LH wave frequency would decrease as is evident from Eq.(10).

Fig.1 The dispersion relation of LH wave(Eq.(10))for different values of spin polarization η =0.047,0.071 and 0.095 corresponding to B0=(2,3 and 4)×1010G and n0=1027cm−3.
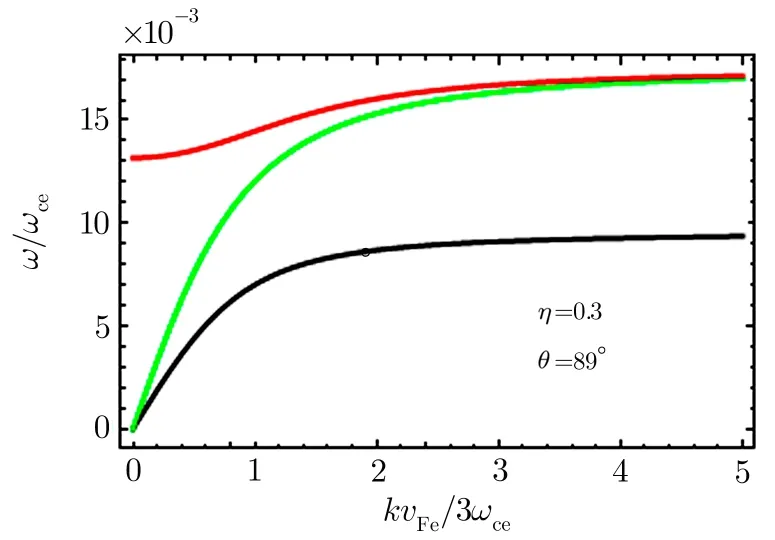
Fig.2 Figure shows the spectra of electrostatic waves propagating nearly perpendicular to magnetic field.The figure depicts dispersion branches of LH wave(upper curve),spin electron acoustic wave(middle curve)and IA wave having lowest frequency.
Forθexactlyπ/2 we have only one wave solution i.e.,LH wave.However,if we consider small deviation fromθ=π/2 and impose constraintωci≪ω≪ωce,the dispersion equation acquires the following form

In the absence of electron spin polarization,the Eq.(11)becomes second degree inω2,and has two real solutions,one is IA wave and the other LH wave.However,Eq.(11),as it is,is cubic inω2and thus has three real wave solutions corresponding to IA and LH waves and a new spin dependent wave called spin electron acoustic wave.It may be pointed out here that the spectra of low frequency longitudinal waves are modi fied due to new electron spin dependent mode,which appears as a result of our consideration of SSE-QHD equations.The dispersion relation(11)is graphically represented in Fig.2.At fixed values of spin polarizationηand the propagation angleθ,the graph depicts three curves with the upper curve describing the LH wave,the middle curve the SEAW and lower curve the IA wave.Also it is clear from the graph that the frequencies of all the three waves first increase at small wave numbers and then become constant at relatively large values.
3.2 Ion Acoustic Wave
If we consider parallel propagation and treat electrons inertialess the dispersion Eq.(9)takes the following form
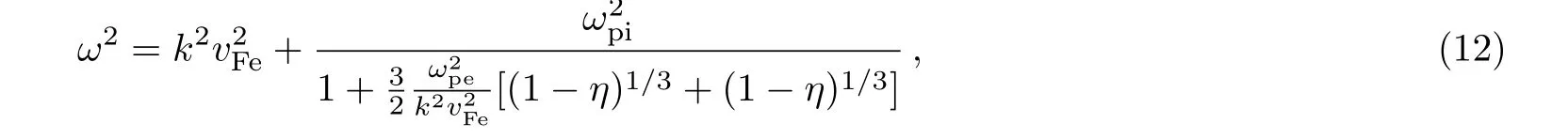

which is the dispersion relation of IA wave in a partially spin polarized degenerate magnetized plasma.In the long wavelength limitω2pe≫k2v2Fe,the above dispersion relation reduces to Herec2Fs=(3π2n0e)1/3ħ/3memithe square acoustic speed in degenerate plasma.Further,for unpolarized plasma(η=0),we get the standard dispersion relation of IA wave in degenerate plasma.The graphical analysis of dispersion relation(13)is shown in Fig.3.From the figure,it is obvious that by increasing spin polarization,the frequency of IA wave reduces.However,without taking long wavelength limit,the frequency of IA wave increases but the increase is negligibly small as shown in Fig.4.It is important to mention here that if we retain the inertia of electrons,the spectrum of IA wave is modi fied with SEAW,which is already reported in Ref.[34].
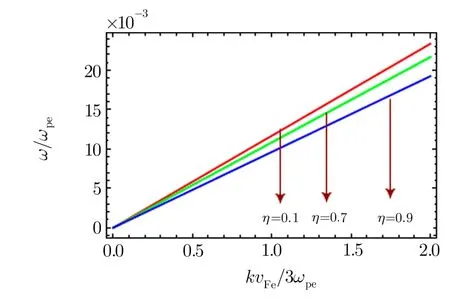
Fig.3 The dispersion relation of IA wave in the limit of long wavelength(Eq.(13))for different values of spin polarization η=0.1,0.7 and 0.9 corresponding to B0=4.20×1010G,2.94×1011G and 3.78×1011G and n0=1027cm−3.
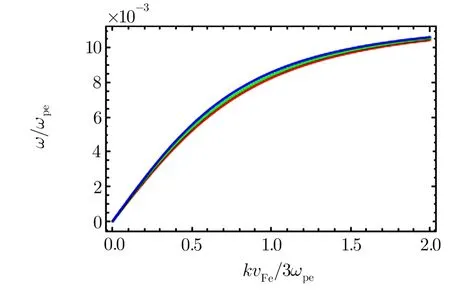
Fig.4 The figure exhibits dispersion character of IA wave without taking long wavelength limit(Eq.(12))for the same parameters as used in Fig.3.
3.3 Ion Cyclotron Waves
An electrostatic IC wave propagates nearly at right angle to the external magnetic field.If the angle is not exactlyπ/2,the electrons can move along the external magnetic field to carry charge from negative to positive region and carry out Debye shielding.The ions cannot do this effectively because their inertia prevents them from moving such long distances in a wave period;this is why we can neglect the parallel propagation of ions.[49]With these assumptions,the dispersion Eq.(9)becomes

which is the modi fied dispersion relation of electrostatic IC waves with spin polarization effects.If we assume that the electrons are inertialess,the above dispersion relation attains the following form

In case of long wave length limitk2v2Fe≪ω2pe,the above dispersion relation reduces to

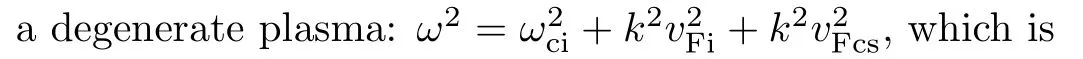
In general,in deriving the dispersion relation of IC wave the electrons are considered to be inertialess.If we retain the inertia of electrons,then the dispersion Eq.(14)becomes cubic inω2,which means that it contains three real wave solutions.If the electrons are treated as single fluid we have only two wave solutions:IA and IC waves.But in case of partially spin polarized plasma we have three wave solutions instead of two.Thus,like LH waves the spectrum of IC waves is also modi fied with the new spin dependent wave.The dispersion Eq.(14)is plotted in Fig.7 for a fixed value of spin polarization.In this plot,the low frequency curve corresponds to IA wave,the middle curve corresponds to SEAW and the upper line shows the IC wave.In Fig.7 left hand side ofy-axis represent magnitude of solid curves(Red,Green,and Blue).As the lower thick blue line seems to be merged withx-axis and is therefore redrawn on the right hand side ofy-axis.Now the blue dashed curve is the actual representation of solid blue curve.
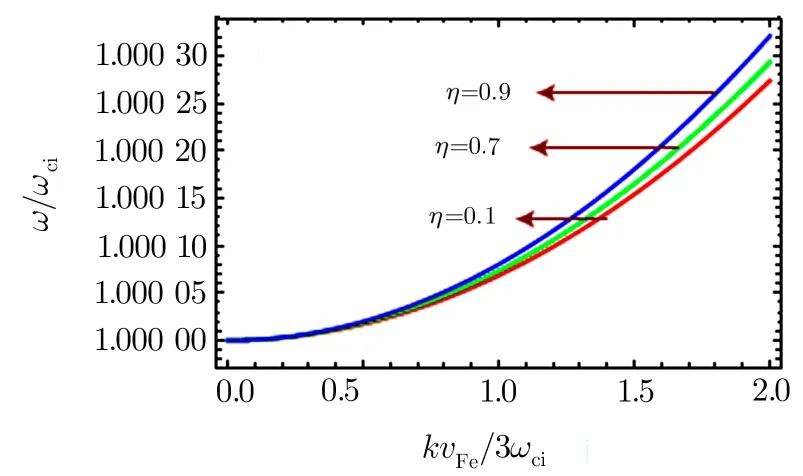
Fig.5 Figure shows the increase in frequency of IC wave(Eq.(15))with increasing spin polarization η using the same parameters as in Fig.3.

Fig.7 (Color online)Figure shows the existence of SEAW in the spectra of IC and IA waves.High frequency curve corresponds to IC wave,middle curve describes SEA wave and lower frequency wave is IA wave.Here,η=0.23 with B0=1011G and n0=1027cm−3.
4 Conclusions
The beauty of SSE is that it generates new wave phenomena in the spectrum of both the electrostatic and electromagnetic waves.Exploring the applications of SSEQHD model,we are probably the first to consider the problem of low frequency longitudinal waves in degenerate magnetized plasma and to have derived the general dispersion relation of longitudinal waves in a partially spin polarized degenerate magnetized plasma.In the spectrum of low frequency electrostatic waves we present analytical and numerical analysis of LH wave,IA wave,and IC wave.For perpendicular propagation,the frequency of LH wave decreases with increasing values of spin polarization(η).However at small deviation from perpendicular propagation,the spectra of LH and IA waves are modi fied with SEAW.Further,signi ficant frequency shifts are observed in the spectrum of IA wave with the variation of spin polarization effects.In case of inertialess electron,the frequency of IC wave increases with increasing spin polarization but if we impose the condition of long wavelength limit the frequency of IC wave decreases with increasing spin polarization.By taking account of inertia of electrons,the spectra of IC and IA waves are also modi fied with SEAW like in LH wave.
Since our chosen parameters are typically found in the pulsating white dwarfs i.e.,n0=(1026–1028)cm−3andB0=(109–1011)G,therefore our present investigations are useful for understanding the existence of new waves and propagation of low frequency electrostatic waves in such dense astrophysical objects.Further,we hope that our findings may shed new light on further study of instabilities and nonlinear structures of electrostatic and electromagnetic waves.

Fig.6 Figure shows the propagation character of the IC wave in limit of long wavelength(Eq.(16)).The parameters are the same as of Fig.3.
[1]T.H.Stix,Phys.Rev.Lett.15(1965)878.
[2]J.F.Drake,J.D.Huba,and N.T.Gladd,Phys.Fluids 26(1983)2247.
[3]D.B.Melrose,Instabilities in Space and Laboratory Plasmas,Cambridge University Press,Cambridge(1986).
[4]V.D.Shapiro,R.Bingham,J.M.Dawson,et al.,Phys.Scr.T 75(1998)39.
[5]I.H.Cairns and B.F.McMillan,Phys.Plasmas 12(2005)102110.
[6]B.F.McMillan and I.H.Cairns,Phys.Plasmas 14(2007)012103.
[7]A.L.Verdon,I.H.Cairns,D.B.Melrose,and P.A.Robinson,Phys.Plasmas 16(2009)052105.
[8]M.Salimullah,I.Zeba,Ch.Uzma,H.A.Shah,and G.Murtaza,Phys.Lett.A 372(2008)2291.
[9]M.Ayub,H.A.Shah,M.N.S.Qureshi,and M.Salimullah,Commun.Theor.Phys.60(2013)623.
[10]A Rasheed,M.Jamil,F.Areeb,M.Siddique,and M.Salimullah,J.Phys.D:Appl.Phys.49(2016)175109.
[11]T.Rimza and P.Sharma,J.Phys:Conf.Series 836(2017)012028.
[12]D.A.Gurnett and L.A.Frank,J.Geophys.Res.83(1978)58.
[13]N.Lin,P.J.Kellogg,R.J.MacDowall,and S.P.Gary,Space Sci.Rev.97(2001)196.
[14]M.Backrud-Ivgren,G.Stenberg,M.Andr,et al.,Ann.Geophys.23(2005)3739.
[15]W.C.Hua,S.X.Xia,and W.C.Qun,Commun.Theor.Phys.53(2010)771.
[16]F.Haas,L.G.Garcia,J.Goedert,and G.Manfredi,Phys.Plasmas 10(2003)3858.
[17]F.Haas and S.Mahmood,Phys.Rev.E 92(2015)053112.
[18]F.Haas and S.Mahmood,Phys.Rev.E 94(2016)033212.
[19]N.D’Angelo and R.W.Motley,Phys.Fluids 5(1962)633.
[20]R.W.Motley and N.D’Angelo,Phys.Fluids 6(1963)296.
[21]S.R.Mosier and D.A.Gurnett,Nature(London)223(1969)605.
[22]M.Kono,J.Vranjes,and N.Batool,Phys.Rev.Lett.112(2014)105001.
[23]J.Sharma and S.C.Sharma,Phys.Plasmas 17(2010)123701.
[24]J.Sharma,S.C.Sharma,and D.Kaur,Prog.Electromagn.Res.Lett.54(2015)123.
[25]T.Sreeraj,S.V.Singh,and G.S.Lakhina,Phys.Plasmas 23(2016)082901.
[26]L.S.Kuz’menkov,S.G.Maksimov,and V.V.Fedoseev,Theor.Math.Phys.126(2001)110.
[27]L.S.Kuz’menkov,S.G.Maksimov,and V.V.Fedoseev,Theor.Math.Phys.126(2001)212.
[28]M.Marklund and G.Brodin,Phys.Rev.Lett.98(2007)025001.
[29]D.V.Vagin,N.E.Kim,P.A.Polyakov,and A.E.Rusakov,Izv.Ranser.Fiz.70(2006)443[Bull.Rus.Acad.Sci.:Phys.70(2006)505].
[30]P.A.Andreev and L.S.Kuz’menkov,Moscow University Phys.Bull.62(2007)271.
[31]G.Brodin,M.Marklund,J.Zamanian,A.Ericsson,and P.L.Mana,Phys.Rev.Lett.101(2008)245002.
[32]A.P.Misra,G.Brodin,M.Marklund,and P.K.Shukla,J.Plasma Phys.76(2010)857.
[33]A.Hussain,M.Stefan,and G.Brodin,Phys.Plasmas 21(2014)032104.
[34]P.A.Andreev,Phys.Rev.E 91(2015)033111.
[35]P.A.Andreev,Ann.Phys.361(2015)278.
[36]P.A.Andreev and Z.Iqbal,Phys.Rev.E 93(2016)033209.
[37]M.Shahid,Z.Iqbal,A.Hussain,and G.Murtaza,Phys.Scr.90(2015)025605.
[38]F.A.Asenjo,J.Zamanian,M.Marklund,G.Brodin,and P.Johansson,New J.Phys.14(2012)073042.
[39]J.Zamanian,M.Marklund,and G.Brodin,New J.Phys.12(2010)043019.
[40]P.A.Andreev,Physica A 432(2015)108.
[41]P.A.Andreev,Phys.Plasmas 23(2016)062103.
[42]P.A.Andreev,Phys.Plasmas 24(2017)022114.
[43]Z.Iqbal,A.Hussain,G.Murtaza,and M.Ali,Phys.Plasmas 21(2014)122118.
[44]P.A.Andreev,Phys.Plasmas 23(2016)012106.
[45]Z.Iqbal and P.A.Andreev,Phys.Plasmas 23(2016)062320.
[46]P.A.Andreev and L.S.Kuz’menkov,EPL 113(2016)17001.
[47]P.A.Andreev,Phys.Plasmas 24(2017)022106.
[48]P.A.Andreev and M.I.Trukhanova,e-print arXiv:1603.07506.
[49]F.F.Chen,Introduction to Plasma Physics and Controlled Fusion,Vol.1,Plenum,New York(1984).
杂志排行
Communications in Theoretical Physics的其它文章
- Rumor Spreading Model with Immunization Strategy and Delay Time on Homogeneous Networks∗
- In fluence of Cell-Cell Interactions on the Population Growth Rate in a Tumor∗
- Damped Kadomtsev–Petviashvili Equation for Weakly Dissipative Solitons in Dense Relativistic Degenerate Plasmas
- General Solutions for Hydromagnetic Free Convection Flow over an In finite Plate with Newtonian Heating,Mass Diffusion and Chemical Reaction
- New Exact Traveling Wave Solutions of the Unstable Nonlinear Schrodinger Equations
- In finite Conservation Laws,Continuous Symmetries and Invariant Solutions of Some Discrete Integrable Equations∗
