航天器缠绕肋天线缠绕过程动力学建模与仿真

易乐天 袁俊刚 董富祥 李友遐

(中国空间技术研究院通信卫星事业部，北京 100094)



航天器缠绕肋天线缠绕过程动力学建模与仿真

易乐天 袁俊刚 董富祥 李友遐

(中国空间技术研究院通信卫星事业部，北京 100094)

航天器缠绕肋天线缠绕过程，涉及柔性大变形与大范围运动的耦合、阻尼因素影响，以及缠绕肋条与中心毂接触碰撞等动力学问题，是获取缠绕肋天线展开特性的重要输入。文章应用空间绝对节点坐标法对缠绕肋天线建模，基于比例阻尼模型推导了阻尼力对绝对坐标列阵的雅克比矩阵，建立了缠绕肋条与中心毂的刚柔耦合系统接触碰撞检测模型。通过对缠绕肋条缠绕过程进行仿真，获得了缠绕肋条缠绕过程的动力学响应，分析了阻尼系数选取对缠绕速度、中心毂接触力的影响，结果可为缠绕肋天线展开过程的动力学分析提供输入，并为缠绕肋天线研制过程中缠绕、展开试验提供参考。

缠绕肋天线；缠绕过程；阻尼影响；空间绝对节点坐标法；接触碰撞

1 引言

缠绕肋天线是一种航天器大口径可展开天线结构形式。它主要由中心毂、缠绕肋条和索网反射面组成。由碳纤维复合材料制成的缠绕肋条，通过铰链连接在中心毂上，并沿中心毂径向伸展出来，用于支撑和保持索网反射面的抛物型面。收拢状态时，缠绕肋条紧紧沿一个方向缠绕在中心毂上；在轨展开时，缠绕肋条依靠自身弹性势能回弹展开。因此，缠绕肋天线收展控制机构简单，展开可靠性高。另外，由于缠绕肋条的大柔性，缠绕肋天线在网面天线中具有最高的收纳比。缠绕肋天线曾应用于美国应用技术卫星-6(ATS-6，口径9.14 m)及“大酒瓶(Magnum)”电子侦察卫星(口径77 m)，分别满足对地观测精度需求以及雷达信号(100 MHz～10 GHz)的侦收需求[1]。国外已进行了600 m口径缠绕肋天线的方案设计，构成的超大口径可展开天线能满足移动通信、对地遥感和深空探测的应用需求[2]。为了满足我国日益增长的对地观测及星地移动通信的应用需求，国内也开展了缠绕肋天线的研制。

获得航天器缠绕肋天线在轨动力学特性，是制定天线缠绕及展开过程控制策略的前提条件，关系到天线在轨展开任务的成败。由于缠绕肋天线尺寸大、质量小，地面试验难以准确掌握其在轨动力学特性，因此进行数值建模仿真成为研究的重要手段。而缠绕肋天线缠绕过程建模仿真，是天线在轨展开过程仿真的重要输入，已有一些研究。文献[3]中采用ABAQUS软件建立了缠绕肋条非线性有限元模型，实现了缠绕过程模拟分析，得到缠绕肋条缠绕过程各阶段动力学参数。文献[4]中应用ABAQUS S4R单元建立了缠绕肋条有限元模型，实现缠绕过程的数值模拟分析，并对缠绕过程动力学参数进行了研究。文献[5]中利用二维绝对节点坐标梁单元对柔性梁的回弹运动过程进行了仿真研究，并进行了相应的试验验证，证明了绝对节点坐标法可准确描述缠绕肋条回弹运动过程。上述研究对缠绕肋条的有限元模型和力学特性进行了分析，但是由于缠绕肋条的大柔性特点，这些研究仍存在以下问题：①缠绕肋条缠绕、展开过程为大变形长时间历程运动问题，而上述研究均基于显式非线性有限元法，在求解长时间历程动力学问题时数值稳定性较差，对于耦合大范围空间运动的动力学问题，难以保证计算精度，甚至会出现完全无法收敛的情况。因此，有必要探索适用于大柔性多体系统的动力学建模方法，并采用隐式方法求解。②在缠绕肋条缠绕过程中，缠绕肋与中心毂存在长时间接触碰撞及阻尼因素影响。因此，须进行接触碰撞检测建模，并讨论阻尼系数设置对仿真结果的影响。

本文以航天器缠绕肋天线动力学建模需求为背景，考虑缠绕肋条缠绕过程的大范围空间运动与大柔性变形的耦合，将空间绝对节点坐标法(ANCF)应用于大柔性缠绕肋天线建模中；同时考虑柔性缠绕肋与刚性中心毂的接触碰撞及回弹过程的阻尼因素影响，采用无条件稳定的隐式方法求解动力学方程，对缠绕肋条缠绕过程进行建模仿真。仿真算例结果表明，本文提出的缠绕肋天线缠绕过程建模方法数值稳定且工程实用，对阻尼因素的分析可指导缠绕肋天线缠绕及展开试验阻尼系数的选取。

2 航天器缠绕肋天线动力学建模

航天器缠绕肋天线在轨收拢状态示意如图1所示。柔性缠绕肋条呈螺旋状逐圈紧紧缠绕在刚性中心毂上，是典型的刚柔耦合多体系统。

图1 缠绕肋天线在轨收拢状态示意Fig.1 Wrapped-rib antenna on orbit in folded status

图2为缠绕肋条缠绕过程示意。缠绕肋条在缠绕过程中有两个特点：首先，缠绕肋条绕中心毂旋转，同时自身发生柔性大变形，因此属于大变形耦合大转动问题；其次，存在由阻尼器、铰链摩擦等因素带来的阻尼影响，以及缠绕肋与中心毂的接触碰撞，产生的阻尼力及接触碰撞力均是时变的，且在整个缠绕过程中都存在，会对稳定性产生负面影响。与环形桁架式天线不同，缠绕肋天线不适合基于小变形假设的混合坐标法进行动力学建模，因为混合坐标法是一种零次近似的柔性多体系统建模方法，在涉及大变形耦合大转动的工程问题建模中将会忽略“动力刚化”现象，使仿真结果失真。文献[6]中提出了绝对节点坐标法，利用其建立的动力学方程具有常数系统质量矩阵，不存在科氏力项，能精确地描述刚柔耦合多体系统的动力学特征。仿真和试验表明，绝对节点坐标法能精确地描述柔性大变形、大转动系统动力学问题[7-8]。本文针对缠绕肋天线大变形耦合大转动的特点，采用空间绝对节点坐标梁单元对缠绕肋天线进行多体动力学建模。建模中引入比例阻尼模型，解决缠绕过程由于摩擦等带来的阻尼问题，并推导了相应的雅克比矩阵；同时，建立了适用于隐式方法的接触碰撞检测模型，以解决缠绕肋条与中心毂在缠绕过程中的接触问题，避免了显式方法数值稳定性不足的问题。

图2 缠绕肋天线缠绕过程示意Fig.2 Wrapping process of wrapped-rib antenna

2.1 空间绝对节点坐标梁单元

如图3所示，文献[9]中提出一种基于绝对节点坐标方法的空间梁单元。

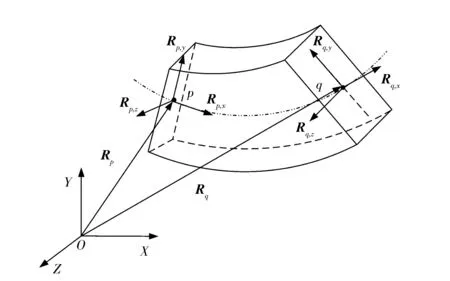
图3 空间绝对节点坐标梁单元Fig.3 Spatial ANCF beam element

图3中，p和q为空间绝对节点坐标梁单元节点。rp和rq分别为向量Rp和Rq在全局坐标系O-XYZ下的位置坐标列阵。向量Rp,x，Rp,y，Rp,z，Rq,x，Rq,y，Rq,z在全局坐标系下的位置坐标列阵分别为rp,x，rp,y，rp,z，rq,x，rq,y，rq,z。其中：rp,x=∂rp/∂x，rp,y=∂rp/∂y，rp,z=∂rp/∂z，rq,x=∂rq/∂x，rq,y=∂rq/∂y，rq,z=∂rq/∂z，(x,y,z)为单元内部任意一点的局部坐标。

在全局坐标系下，单元内部任意一点的位置列阵可表示为

r=Se

(1)

式中：e为单元的绝对坐标列阵，共有24个分量，见式(2)；S为空间绝对节点坐标梁单元的形函数，见式(3)。

(2)

(3)

式中：I为3×3的单位矩阵；S1=1-3ξ2+2ξ3；S2=l(ξ-2ξ2+ξ3)；S3=l(η-ξη)；S4=l(ζ-ξζ)；S5=3ξ2-2ξ3；S6=l(-ξ2+ξ3)；S7=lξη；S8=lξζ；ξ=x/l，η=y/l，ζ=z/l，l为单元长度。

2.2 单元弹性力及其对绝对坐标列阵的雅克比矩阵

空间绝对节点坐标梁单元弹性力为

Fe=Kee

(4)

式中：单元刚度矩阵Ke为绝对坐标列阵e的函数，是时变的高度非线性矩阵，为提高计算效率，可将其分解为与绝对坐标列阵无关的常数刚度矩阵K1与绝对坐标列阵相关的非线性刚度矩阵K2之和，见式(5)。

(5)

(6)

(7)

式中：((∂S/∂α)T(∂S/∂α))i的下标代表矩阵(∂S/∂α)T·(∂S/∂α)的第i行；下标j以此类推；i,j=1，2，…，24；β=1,2,3。

单元弹性力对绝对坐标列阵的雅克比矩阵的第i行、第k列(k=1，2，…，24)元素，同样可用不变矩阵表进行计算，见式(8)。

(8)

式中：ej表示绝对坐标列阵e的第j个分量。

用不变矩阵表示刚度矩阵及其雅克比矩阵，可将刚度矩阵中时变部分从单元内部积分中分离出来，将不变矩阵提前储存于计算机中，提高计算效率。

2.3 单元阻尼力及其雅克比矩阵推导

缠绕肋天线肋条缠绕过程中，存在阻尼器作用、铰链摩擦等阻尼影响。阻尼器一般安装在缠绕肋条与中心毂连接铰链处，用于减缓缠绕展开过程中产生的冲击。由铰链摩擦与阻尼器产生的阻尼力(力矩)一般作用于连接铰链处。为了把这些阻尼因素引入缠绕肋天线动力学模型，须计算缠绕肋条与中心毂连接单元的单元阻尼力列阵，并按节点编号集成为系统阻尼力列阵。为简化数学分析，采用黏性阻尼模型建立单元阻尼力与广义速度的关系，单元阻尼力列阵为

(9)

采用常用的比例阻尼模型[11]建立单元阻尼矩阵与单元质量矩阵、单元刚度矩阵的关系，见式(10)。

Ce=aMe+bKe

(10)

式中：a，b为阻尼系数，可由材料阻尼特性试验确定。

革新教学管理，树立现代化教学管理理念，不仅是深化课程体系与教学内容的前提与基本条件，更是实践创新性人才培养的有效保障。四年制高职与三年制高职及普通本科的根本区别是培养目标的类型不同，而非层次不同[7]。四年制高职公共基础课的教学模式、课程设置、师资建设等都要围绕着培养目标而制定，四年制高职学生所具备的职业技能与能力的科技含量更高、技能水平更高、人文素质更高，因此革新四年制高职公共基础课教学管理理念，注重培养学生实践能力、拓宽专业适应面；加强公共基础课程建设，强化岗位群所需基本素质，为学生迅速适应岗位环境与可持续发展提供强有力的动能。

(11)

(12)

式中：h为广义α法的步长；β=1/(ρ+1)2；广义α法的谱半径γ=1/2+2/(ρ+1)，ρ∈[0,1]，γ决定了算法的计算效率和稳定度，该参数的选取方法可参见文献[12]。

由于Me为常数质量阵，有

(13)

结合式(12)及式(6)，可得

(14)

式中：s=1,2,…,24。

结合式(13)及式(14)，可得阻尼力列阵对绝对坐标列阵的雅克比矩阵第i行、第k列元素为

(15)

由此，获得单元阻尼力对绝对坐标列阵的雅克比矩阵，按单元编号集成后即可获得系统阻尼力对系统绝对坐标列阵的雅克比矩阵。

缠绕肋天线缠绕过程中，缠绕肋条与中心毂有时变的接触与碰撞力。产生接触碰撞的区域以及碰撞力的大小方向，在碰撞发生之前是未知的。因此，须检测碰撞发生的位置和时刻，获得时变的单元碰撞接触力列阵，并集成到基于空间绝对节点坐标法建立的系统动力学方程中。

如图4所示，在空间绝对节点坐标法中，刚柔耦合系统内部任意一点的位置坐标，都在全局坐标系下描述，因此接触碰撞检测也要在全局坐标系下进行。在缠绕肋条单元节点及其内部布置若干检测点，对检测点处是否发生接触碰撞提出如下判据。

如图4所示，RO为全局坐标系原点O至检测点的向量，ROO′为全局坐标系原点至中心毂圆心O′的向量，RO′为中心毂圆心至检测点的向量，N为接触碰撞法向力的方向向量，它们在全局坐标系下的列阵分别记为rO，rOO′，rO′，n。Rh为中心毂半径。首先，计算检测点浸入深度δ=Rh-|rO′|=Rh-|rO-rOO′|。当δ>0时，认为在该检测点处发生碰撞或接触。

在检测到接触碰撞后，利用等效弹簧阻尼模型计算碰撞力的大小。其基本思想为：根据Hertz定律确定弹簧接触力，同时加入阻尼因子模拟摩擦等因素造成的能量损失。因此，碰撞力的大小取决于等效弹簧的刚度特性和阻尼特性，在此模型下作用于接触点的接触碰撞力列阵为

(16)

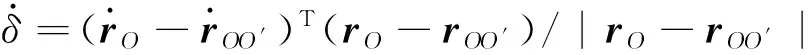
将作用于检测点的接触碰撞力分布于空间绝对节点坐标梁单元节点上，可得单元接触碰撞力列阵为

(17)

图4 缠绕肋条与中心毂的接触碰撞检测Fig.4 Detection of contact between wrapped-rib and central hub

为提高检测精度，可在每个单元内部布置若干检测点，在每个检测点上进行接触碰撞检测，最后将各个接触点处产生的接触力集成为单元接触力。为提高检测效率，可首先对单元外部节点进行粗检测，再针对各个单元内部检测点进行精检测。

3 仿真算例

3.1 刚柔耦合系统动力学方程及求解

基于上述推导，将第2节所述单元质量矩阵、弹性力列阵等矩阵和列阵按单元编号进行集成，得到相应的系统矩阵和列阵。可建立缠绕肋条与中心毂这一刚柔耦合多体系统的动力学模型为

(18)

式中：u为系统在全局坐标系下的绝对坐标列阵；t为仿真时间；M为系统质量矩阵；lλ为拉格朗日乘子列阵；Q为系统广义外力列阵；F为系统弹性力列阵；QC为系统阻尼力列阵；Qct为系统接触碰撞力列阵；Φ为系统约束方程组成的列阵；Φu为Φ对系统绝对坐标列阵u的雅克比矩阵。

式(18)为多体系统动力学计算中“指标3”[14]的代数微分方程，可采用无条件稳定的广义α方法[12]进行编程求解。

3.2 缠绕过程仿真分析

缠绕肋条与中心毂的初始状态如图5所示：中心毂为直径1.2 m、高度3 m的刚性圆柱体，密度为7810 kg/m3。缠绕肋条截面高0.03 m，截面宽0.000 3 m，长12 m。密度为1600 kg/m3，弹性模量为5 MPa，泊松比为0.3。设置等效接触刚度Kn为1×106，碰撞阻尼系数c为1×103。

图5 缠绕肋条与中心毂的初始状态Fig.5 Initial state of wrapping-rib and central hub

缠绕肋条划分为10个空间绝对节点坐标梁单元，边界条件为刚性中心毂两端固支，柔性梁一端与中心毂铰支。设缠绕肋条受到平行于中心毂轴线方向的常力矩，算法步长取为0.5s，仿真结果如图6所示。可见，应用空间绝对节点坐标法建立的中心毂-缠绕肋条模型，反映了柔性缠绕肋条的大变形，以及它与刚性中心毂产生的碰撞过程，能体现出缠绕肋条逐渐呈螺旋缠绕在中心毂上这一过程，可作为回弹过程仿真的输入。

通过设置不同的阻尼系数，可得到缠绕肋条在同一力矩驱动作用下不同的速度响应曲线。图7分别为阻尼系数a为0.0，0.2，0.5的缠绕肋条端点线速度随时间变化曲线。可见，阻尼系数增大使得速度峰值下降，且峰值出现的时间推后。

图8为发生接触碰撞的接触检测点个数随时间变化曲线。图8中显示，随着缠绕肋条逐步缠紧在中心毂上，两者发生接触的区域逐渐增加。图9为中心毂表面所受接触力幅值随时间变化曲线，随着缠绕肋条不断缠紧，接触力逐渐增大，符合相应物理规律。因此，第2.4节建立的接触碰撞模型能够有效仿真缠绕肋条与中心毂的碰撞现象。

图7和图9中的曲线可说明，适当增大阻尼系数a，不仅可降低缠绕肋条展开端点速度，同时可减小中心毂所受到的接触力冲击。仿真选取的阻尼系数a，可指导连接铰链处阻尼器参数的选取，并可确定缠绕肋天线研制过程中缠绕及展开试验的控制力矩。

图6 缠绕肋条缠绕时间历程Fig.6 Time course of wrapped-rib’s wrapping process

图7 不同阻尼系数下的缠绕肋条端点线速度幅值随时间变化曲线Fig.7 Velocity amplitude of wrapped-rib’s endpoint versus time in different damping coefficients

图8 发生接触的检测点个数随时间变化曲线Fig.8 Number of detection points with contact versus time

图9 中心毂表面所受接触力幅值Fig.9 Contact force amplitude on surface of central hub

为比较隐式求解的空间绝对节点坐标法与显式非线性有限元法在计算效率及数值稳定性方面的差异，本文基于LS-DYNA软件建立了同一物理模型的显式有限元模型，设置阻尼系数a为0，进行仿真计算。2种不同方法所得缠绕肋条端点线速度幅值随时间变化曲线，如图10所示。由于LS-DYNA软件中的接触碰撞参数是根据材料特性自动选取的，因此所得动力学响应与本文建立的方法有所不同，但从图10可见，端点的速度变化趋势基本吻合，验证了空间绝对节点坐标法应用于缠绕肋天线缠绕过程仿真的有效性。

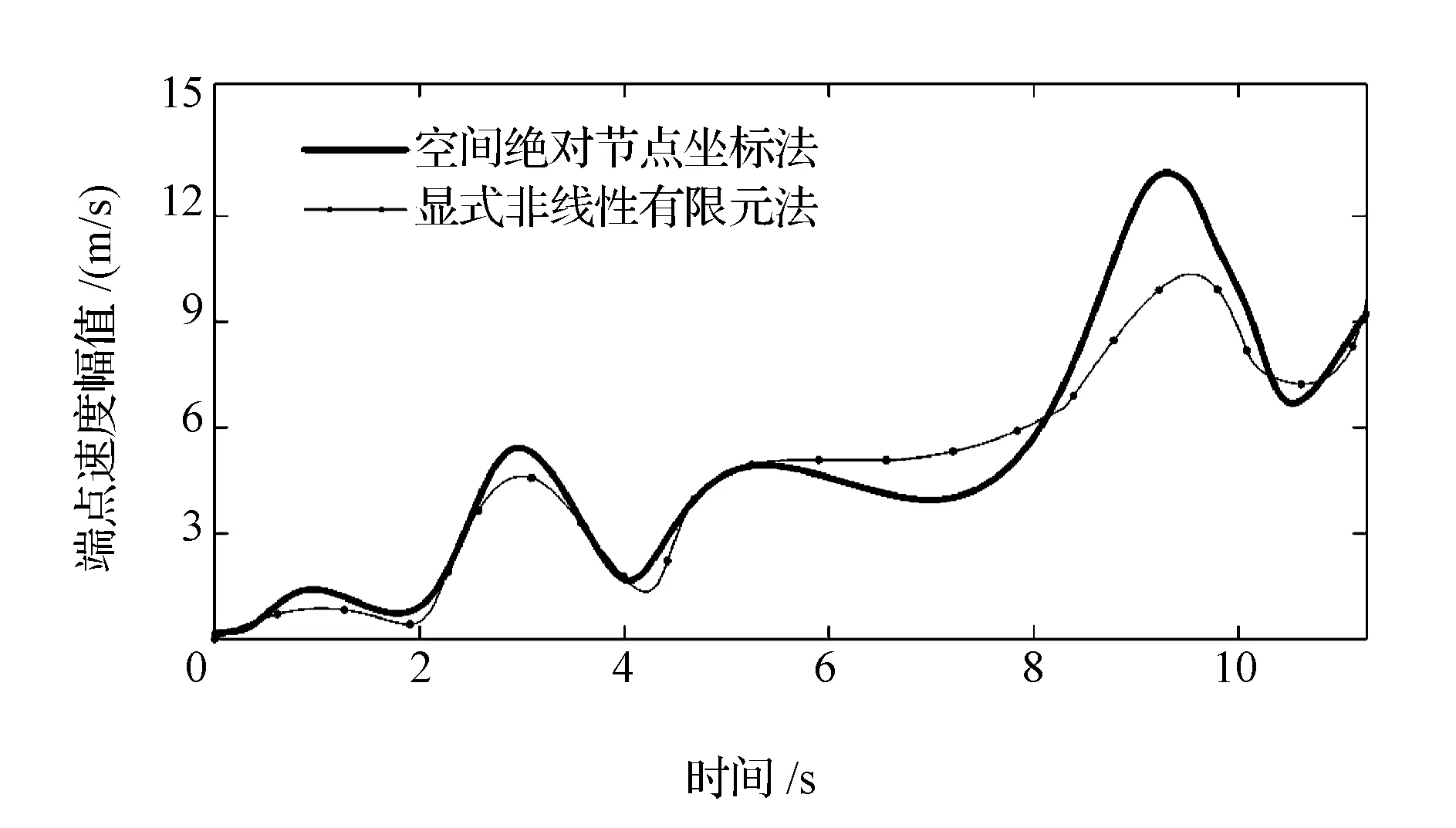
图10 2种方法缠绕肋条端点线速度幅值随时间变化曲线对比Fig.10 Velocity amplitude comparison of wrapping-rib’s endpoint between two methods

表1列出了采取不同时间步长时，2种方法在同一计算平台下所耗CPU时间对比。可以看出，空间绝对节点坐标法求解CPU耗时较短。显式非线性有限元法的数值稳定性受时间步长限制，取时间步长为0.5s时会出现发散的情况。由此可以看出，基于隐式求解的空间绝对节点坐标法，在数值稳定性上优于显式求解法。

表1 2种方法所耗CPU时间对比

4 结论

本文将空间绝对节点坐标法应用于柔性缠绕肋天线建模，并考虑阻尼因素影响，建立了缠绕肋-中心毂系统的刚柔耦合多体系统接触碰撞模型，进行了缠绕过程仿真分析，得到如下结论。

(1)空间绝对节点坐标法可解决缠绕肋天线大变形与大转动耦合问题，能够精准描述缠绕肋条的运动过程，同时可解决显式求解方法数值稳定性不足的问题。

(2)本文推导建立的单元阻尼力雅克比矩阵，能够适用于空间绝对节点坐标法，数值仿真所选取的阻尼系数，可进一步指导缠绕试验阻尼器的选取。

(3)本文建立的接触碰撞检测模型，反映了缠绕肋条与中心毂的碰撞过程，仿真结果符合缠绕肋条实际缠绕过程，可为缠绕肋天线的展开过程动力学分析提供输入，并为缠绕肋天线缠绕过程试验提供依据和参考。而且，本文提出的建模仿真方法，同样适用于缠绕肋天线展开过程仿真。

References)

[1] 周彩根,樊昀.静止轨道电子侦察卫星发展趋势展望[C]//中国电子学会电子对抗分会第十三届学术年会.北京：中国电子学会，2003:71-77

Zhou Caigen，Fan Yun. Prospects for the development of electronic geostationary reconnaissance satellite[C]//Proceedings of the 13th Conference of Electronic Countermeasures of Chinese Institute of Electronics. Beijing： The Chinese Institute of Electronics，2003: 71-77 (in Chinese)

[2]董志强，段宝岩.星载天线缠绕肋条的力学特性研究[J].西安电子科技大学学报(自然科学版)，2001，28(6):755-758

Dong Zhiqiang，Duan Baoyan. Study of the behavior mechanics of the extendible satellite antenna with the type of twinning ribs[J]. Journal of Xidian University (Na-tural Science)，2001，28(6): 755-758 (in Chinese)

[3]李瑞雄，陈务军，付功义，等.透镜式缠绕肋压扁缠绕过程数值模拟分析[J].宇航学报，2011，32(1)： 224-231

Li Ruixiong，Chen Wujun，Fu Gongyi，et al. Numerical simulation o flattening and wrapping process of lenticular wrapped rib[J]. Journal of Astronautics，2011，32(1): 224-231 (in Chinese)

[4]邹涛，陈务军，彭福军，等.透镜式缠绕肋收展过程数值模拟分析[J].哈尔滨工程大学学报，2012,34(2):151-156

Zou Tao，Chen Wujun，Peng Fujun，et al. Numerical simulation of stowing and deploying process of lenticular wrapped-rib[J]. Journal of Harbin Engineering University，2012，34(2): 151-156 (in Chinese)

[5]孙智超.基于绝对节点坐标法的柔性结构动力学建模与仿真[D].西安：西安电子科技大学，2012

Sun Zhichao. Analysis and simulation on dynamics of flexible structures using absolute nodal coordinate formulation[D]. Xi’an: Xidian University，2012 (in Chinese)

[6]Shabana A A. An absolute nodal coordinates formulation for the large rotation and deformation analysis of flexible bodies，Technical Report. No. MBS96-1-UIC[R]. Chicago：University of Illinois，1996

[7]Gerstmayr J，Shabana A A. Analysis of thin beams and cables using the absolute nodal coordinate formulation[J]. Nonlinear Dynamics，2006，45: 109-130

[8]Olivier A Bauchau，Shilei Han，Aki Mikkola，et al. Experimental validation of flexible multibody dynamics beam formulations[J]. Multibody System Dynamics，2015，34(4): 373-389

[9]Yakoub R Y. A new three dimensional absolute coordinate based beam element with application to wheel/rail interaction[R]. Chicago: University of Illinois，2001

[10] García-Vallejo D，Mayo J，Escalona J L，et al. Efficient evaluation of the elastic forces and the Jacobian in the absolute nodal coordinate formulation[J]. Nonlinear Dynamics，2004，35: 313-329

[11]Clarence W de Silva.振动阻尼、控制和设计[M].李惠彬，张曼，侯蕾，等译.北京:机械工业出版社,2013:8-9

Clarence Wde Silva. Vibration damping，control，and design[M]. Li Huibin，Zhang Man，Hou Lei，et al. translated. Beijing: China Machine Press，2013: 8-9 (in Chinese)

[12]Arnold M，Bruils O. Convergence of the generalized―a scheme for constrained mechanical systems[J]. Multibody System Dynamics，2007，18: 185-202

[13]Khulief Y A，Shabana A A. A continuous force model for the impact analysis of flexible multibody systems[J]. Mechanism and Machine Theory，1987，22(3): 231-224

[14]刘延柱，潘振宽，戈新生.多体系统动力学[M].2版.北京：高等教育出版社，2014:324-329

Liu Yanzhu，Pan Zhenkuan，Ge Xinsheng. Dynamics of multibody systems[M]. 2nd ed. Beijing: Higher Education Press，2014: 324-329 (in Chinese)

(编辑：夏光)

Dynamics Modeling and Simulation of Wrapping Process for Spacecraft Wrapped-rib Antenna

YI Letian YUAN Jungang DONG Fuxiang LI Youxia

(Institute of Telecommunication Satellite，China Academy of Space Technology，Beijing 100094，China)

The wrapping process of wrapped-rib antenna involves the coupling effect between flexible large deformation and large range motion，as well as the damping effect and the contact collision between the wrapped-rib and the central hub. It is the key input for the deployment simulation of wrapped-rib antenna. The modeling of wrapped-rib is completed using the spatial ANCF (absolute nodal coordinate formulation)，and the Jacobi matrix for absolute nodal coordinates is deduced based on the proportional damping model. The rigid-flexible coupling system’s contact and collision detection model of wrapped-rib and central hub is established. The dynamic process of the wrapped-rib is obtained by simulation，and the influences of the damping coefficients to wrapping velocity and the impact force on central hub are also analyzed. These results can provide input for the dynamic analysis of wrapped-rib antenna deploying process，and a reference for the wrapping and deploying test of wrapped-rib antenna.

wrapped-rib antenna； wrapping process； damping effect； spatial ANCF(absolute nodal coordinate formulation)； contact and collision

2016-12-29；

2017-03-16

国家自然科学基金(11402281)

易乐天，男，硕士研究生，研究方向为航天动力学。Email：yiletian@foxmail.com。

V414

A

10.3969/j.issn.1673-8748.2017.02.014