递归拟合测井高斯曲线快速实现岩性识别

2017-05-08马百征许艳争黎小伟龙利平范久宵

测井技术 2017年1期

马百征,许艳争,黎小伟,龙利平,范久宵

(中国石油化工股份有限公司华北分公司勘探开发研究院,河南郑州 450006)

0 引言

测井曲线形态存在的波动变化,可以用信号分析方法对曲线波动变化趋势分析进行岩性识别和地层层序划分。陈钢花等[1]用小波时频分析测井曲线的频率能量变化进行岩性识别和地层层序的划分,付文钊[2]、李江涛等[3]用小波变换和希尔伯特-黄变换对测井曲线值的突变变化分析进行岩性识别和地层层序划分。考虑到小波变换、希尔伯特-黄变换等侧重分析样点数值的趋势变化,实际地层岩性不同是因矿物元素含量、物性结构比例不同,是其样点值统计的概率分布不同,可以从分析测井数值概率分布的角度进行岩性识别。

根据赵志飞等[4]、毕林锐等[5]的著述,可以用正态分布对地层的岩性、物性分布规律进行表述,某种岩性的测井数值在其值域内的分布规律可以认为遵循正态分布。

岩性特征值可以以高斯概率的方式表述,以其岩性值的高斯曲线特征形态进行岩性识别。直观上可以对于1条测井曲线进行逐点逐段的高斯拟合并求出高斯曲线参数进行岩性识别,但该方法分段过小会受到样点趋势变化的影响并且计算量会很大。根据岩性样点概率统计与样点数值趋势和数量多少无关的特性,利用测井曲线整体曲线包络是所有局部曲线包络叠加的特点,可以先计算出某井全井段的岩性包络,由于全井段的岩性包络为各井段不同岩性包络的叠加,其拟合出的高斯曲线必定与标准的单一岩性高斯曲线不符,但可以对全井进行分段计算包络、拟合高斯曲线,当分段拟合的高斯曲线符合某种岩性的高斯曲线特征时可以判断出该井段的岩性。求取某段岩性时要先求取包含该段的上一井段曲线的包络,计算起始需要给出全井段的曲线包络,该算法过程可以认为是一个递归计算过程。

1 实现方法

1.1 测井曲线直方差包络的求取

通常,一段岩性概率值测井曲线的直方差是一段不连续的折线。以某工区A井自然伽马测井曲线为例,图1中红色折线为测井曲线的部分井段的直方差曲线,直方差数值只是1组测量数据在有限N次统计的结果,考虑到随着N的增加不连续点之间概率存在的可能性也在增加,需要求出1组光滑的曲线包络表示真实的概率。对于概率曲线,其曲线的极值就是信号的包络值。首先找出该曲线的极值点,由于极值点存在不等距的情况,需要将其进行光滑插值[6-7]得到其包络曲线(见图1蓝色曲线)。

图1 A井全井段自然伽马直方差包络曲线

图1中,所有曲线直方差数值均在其曲线包络之内,包络曲线紧密覆盖直方差曲线,包络曲线形态与直方差曲线形态一致。直方差的一阶包络曲线可以认为是测井曲线值概率在其值域的最优表示。

1.2 测井曲线包络的高斯拟合

对于一段井深的测井曲线包络,其本身形态的复杂性和概率分布的偶然性很难仅从其形态进行岩性判定。图1曲线包络中的左侧曲线峰为砂岩峰,右侧为泥岩峰,单从图1整体的曲线包络很难判断出该段岩性是砂岩还是泥岩、粉砂质泥岩、泥质砂岩等。根据测井数值遵循的高斯分布规律,可以对其曲线包络进行高斯拟合,根据拟合出的高斯曲线参数进行岩性判断。标准的高斯分布的概率密度为

(1)

式中,μ为期望值;σ为标准方差。

根据讨论的实际情况,对于一段自然伽马测井数据可以将其视为1组离散数据(xi,yi)(i=1,2,3,…),其中x为井深,y为自然伽马值。该数据符合高斯分布,可表示为

(2)

(3)

式中,Y和F、S可以理解为高斯曲线的峰值、峰值位置、半宽信息。在本文中峰值位置F、半宽信息S为高斯曲线最重要参数,在后述中将用峰值F表示岩性值、半宽信息S表示岩性的单一性。

对于高斯拟合曲线的参数F、S值求取常见的如迭代算法[8],但迭代算法需要事先给定模型且计算量很大,如果给定初始模型不合适,难求得正确的结果。考虑到初始模型给定的复杂性和迭代的计算量以及对于F、S的求取可采用的算法,对式(3)等式两边取自然对数得到等式

(4)

将式(4)整理

(5)

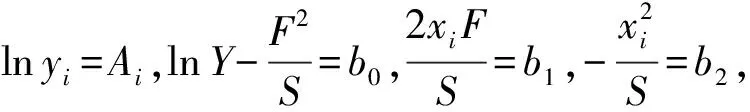
(6)

简写成

A=XB

(7)

式中,A、X矩阵为实际观测的已知数据矩阵,根据广义最小二乘原理可求出最终的矩阵

B=(XTX)-1XTA

(8)

通过矩阵B可以求出峰值位置F、半宽信息S。图2为某工区B井部分井段的声波直方差曲线包络(红色)和拟合出的高斯曲线(蓝色)。

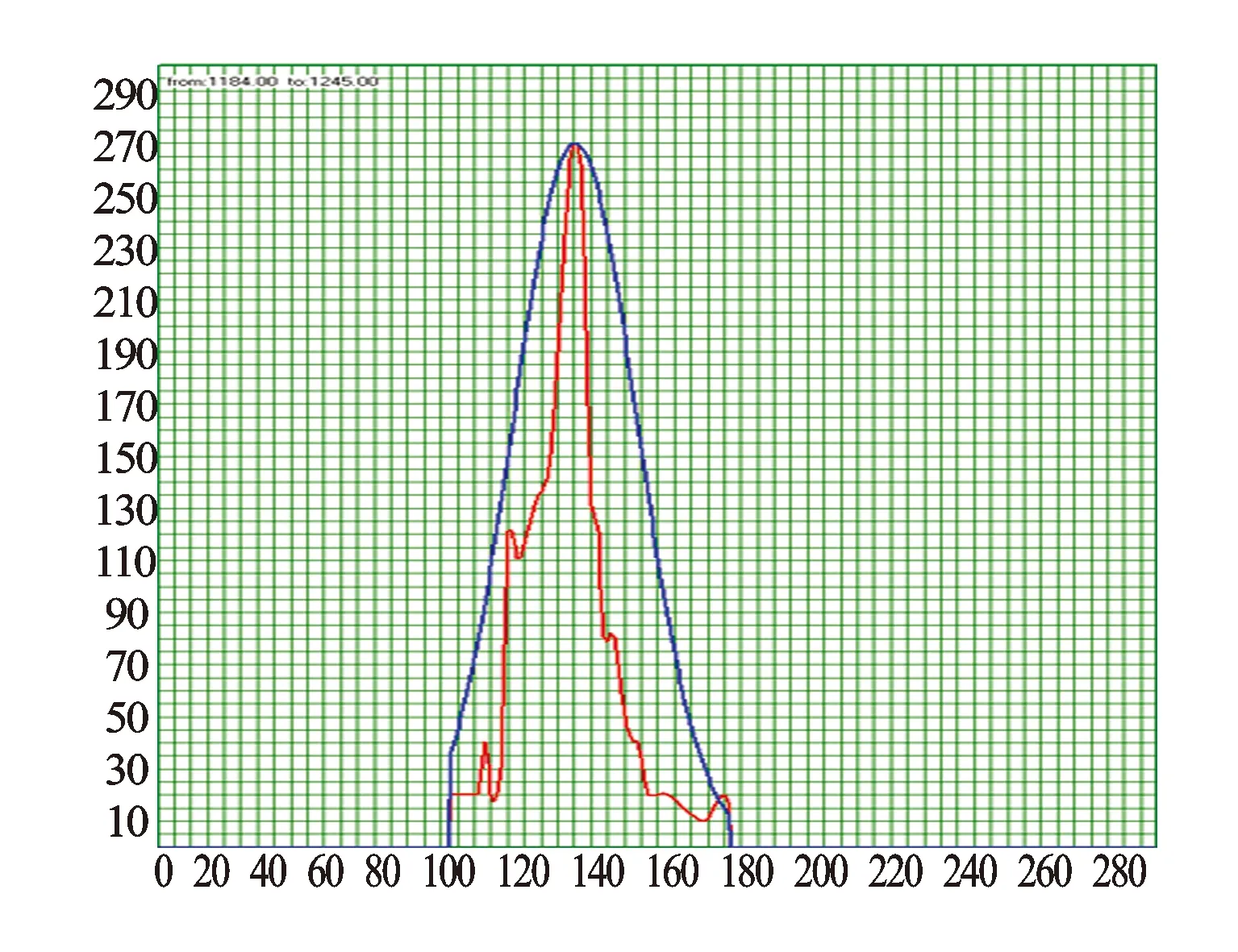
图2 B井部分井段声波高斯曲线

1.3 利用高斯曲线参数进行岩性识别方法

图3 各种岩性的高斯曲线

图3的(a)、(b)、(c)、(d)分别为各种岩性对应的自然伽马曲线包络(红色)和高斯拟合曲线(蓝色)。图3(a)为全井段高斯曲线(泥岩砂岩混合F=109,S=32);图3(b)为砂岩段(含少量泥岩F=100,S=43);图3(c)为粉砂质泥岩(F=110,S=17);图3(d)为泥质砂岩(F=81,S=22)。图3(a)由于是全井段的自然伽马,数值统计井段里含有泥岩和砂岩,曲线包络上会出现2个明显的峰,分别是左侧砂岩峰和右侧泥岩峰;图3(b)段由于是大段砂岩含少量泥岩,曲线包络有明显的砂岩峰和低幅的泥岩曲线显示;图3(c)和图3(d)均为岩性成分较为单一的粉砂质泥岩和砂质泥岩,它们的曲线包络虽然有距离很近的几个尖峰,但认为是1个峰。通过以上曲线包络拟合计算结果可知,当统计的岩性段不为单一岩性时,其曲线包络会出现各自对应的岩性峰,拟合之后的高斯曲线为几个峰值的拟合结果,其曲线幅度较宽,半宽值S会较大,峰值F值反映的是混合岩性值,不能反映真实的岩性[见图3(a)、图3(b)];相反,如果岩性较为单一,则曲线较窄,半宽信息S会很小,峰值F可以反映真实的岩性[见图3(c)和图3(d)]。因此,可以通过井段包络的高斯拟合曲线参数半宽信息S和峰值数值F识别岩性。

2 应用情况

2.1 对区域已知井标准岩性高斯曲线形态调查

在对一个工区通过测井高斯曲线进行岩性识别之前,首先要调查已知井岩性的测井直方差高斯曲线参数的分布特征,了解已知岩性和测井直方差高斯曲线参数之间的关系。图4(a)为A井卡本图上的砂岩段(深度250～350 m),图4(b)为对应的自然伽马曲线包络(红色)和拟合出的高斯曲线(蓝色),其中图4(b)图高斯峰值位置F为59,半宽信息S为8.4。图4(c)为A井卡本图上的泥岩段,图4(d)为该段泥岩自然伽马高斯曲线,峰值F为125,半宽信息S为18.4。用同样的方法对该工区一系列已知井进行调查可以得到该区域的砂岩泥岩的高斯曲线参数(见表1)。表1系列测试数据显示,该工区砂岩峰值位置主要分布在50～90,半宽信息在小于20;泥岩的峰值分布范围100～150,半宽信息小于35。

表1 某区系列井砂岩、泥岩测井高斯曲线的调查情况

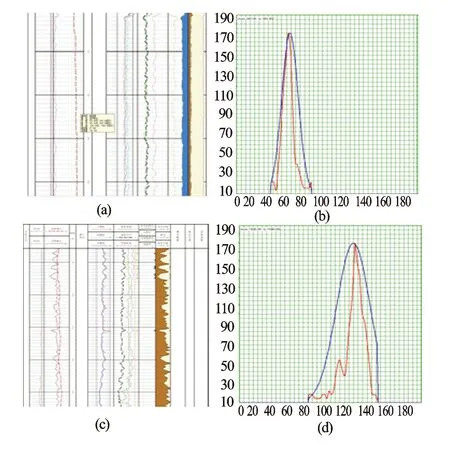
图4 A井泥岩、砂岩与其对应的自然伽马高斯曲线

2.2 用高斯拟合递归进行岩性识别的过程

图5 递归分离包络识别岩性过程

递归是利用当前结果逐渐向后递推计算直到得到最终结果的计算过程[9],相对于穷举法,计算效率更高,根据其算法原理可以设计出很多精巧高效的程序代码[10]。本文由于整条测井曲线的岩性包络为该井所有岩性包络的叠加,需要用递归的方法将测井曲线包络逐步分离并进行高斯曲线拟合。首先对1条测井曲线包络进行高斯拟合出整条曲线的岩性参数,当参数不满足单一岩性时继续对当前井段分段算拟合计算,直到分段的曲线岩性参数确定为单一岩性时终止分段拟合。理论上,无论泥砂岩怎么交错,通过逐次对井段的测井曲线包络的分离拟合,整个井任意井段的岩性都可以识别出来。

以图5的A井为例进行实际运算。首先将全井段自然伽马曲线包络和拟合高斯曲线求出[见图5(a)],由于全井段包含泥岩和砂岩,岩性并不单一,拟合出的高斯曲线半宽信息S过大,峰值F所在位置不能反映真实的岩性,需要继续分段求取曲线包络和高斯曲线,将A井段的岩性等分,分别求出A井的上半段曲线包络和拟合高斯曲线图5(b)和下半段曲线包络和拟合高斯曲线图5(c);显然从图5(b)、图5(c)上,岩性还不是单一岩性,需要继续分段求取包络和拟合高斯曲线参数。继续对其中的一段进行分段[见图5(d)、图5(e)、图5(f)、图5(g)、图5(h)、图5(i)],直到岩性为单一岩性[见图5(h)]。图5(i)中,统计的深度正好处于岩性分界面,包络会出现极端数值过大的2个岩性峰,导致拟合参数出错,曲线包络无法拟合出其分段正确的高斯曲线,需要继续对其分段拟合计算。表2为对某区的一个标准井拟合计算情况。

表2中的D1、D2分别为分段的起始深度和结束深度,运算过程是首先对全井段进行分段,再选择其中不符合单一岩性的井段。本文以上段为起算点进行逐步分段,直至求出最上段的井岩性值,将剩下的井段当作一个未知井段重复以上过程,最后求出全井段岩性值。通过表2数据和已知卡奔图上的岩性对比,解释结果与递归高斯拟合分析结果基本一致,认为该方法可以应用于基于自然伽马测井数值的岩性识别。