低速同轴阵列电容法测量含水率的新理论模型
2017-05-08于宝于靖民孔垂广邢军
于宝,于靖民,孔垂广,邢军
(1.东北石油大学地球科学学院,黑龙江 大庆 163318; 2.辽河油田公司兴隆台采油厂,辽宁 盘锦 124010; 3.中国石油集团测井有限公司,陕西 西安 710200)
0 引 言
含水率是油井产液剖面中的重要测量参数之一。经过多年来许多学者的不断研究,目前国内外对油井含水率的测量尝试了许多方法。譬如,电容法、电导法、分离法、探针法、密度法、射线法、微波法、光学法、热学法、过程层析成像法、快速关断法、超声法、核磁共振法、多传感器组合法等,并形成了一套相应的测井数据解释方法。同轴电容法是最基本的方法,其油水测量的高灵敏度、受油井水矿化度影响小、信号稳定等优点已被业界广泛认同。当油井中不同含水率的油水混合物通过同轴电容传感器2个电极的环形空间时,其电容将随含水率的不同而产生相应的变化,因此,测量这种变化再通过相应的解释模型可以反演出含水率。目前,针对同轴电容传感器,国内外许多学者根据油水不同的状态或解决的问题建立了许多理论和应用模型。这些模型归纳起来有几种:基于油相连续的过流式环形空间内混合流体介电常数与含水率间的关系建立的模型[1-4];基于垂直井环形空间流体取样后油水分离的水相高度与含水率间关系建立的模型[5];基于低频过流式泡状流环形空间内等效电容外电极的内径变化与含水率间关系建立的模型[6-7]。
本文基于研制的同轴阵列电容含水率传感器[8],考察了其结构和特性实验中油水运动状况,发现低速呈泡状或段塞状的油水介质在这种传感器中,其油相趋于在传感器内外电极处流动,传感器内含水率的变化导致传感器电容的变化是由覆盖在同轴电容内电极绝缘层上的油相滞留层厚度的增减引起的。根据这一现象结合流体力学及相关理论,建立了一种新的同轴电容法测量含水率的理论模型。
1 同轴电容含水率模型建立
1.1 模型推导
流体力学研究表明[9],低速黏性流体通过圆管时,会产生平流运动。由于毛细管压力的存在,运动的流体在圆管的截面上表现为从圆管中心一定距离位置开始至管壁处,其流速由最大逐渐变为0。对于由油和水组成的两相流,同一温度下,水的黏度要小于油的黏度,水的密度要大于油的密度。当这2种互不相溶的介质一起流过传感器的内、外电极间的环形空间时,油相介质趋于在环形空间靠电极的区域流动,而水则趋于在环形空间中心流动,因此,在测量电极周围形成了油相滞留层,其厚度将随含水率、流量、电极结构、材料、流体黏度、温度等变化。
研制的阵列同轴电容含水率传感器是在铜质截面上均匀分布6个内电极带绝缘层的同轴电容器。每个电容器的长度为40 mm,内电极外径为2.5 mm,包裹的绝缘层厚度为0.25 mm,外电极内径为6 mm。对于低速油水两相流,在泡状流和段塞流下,即使是较小的油泡,传感器对油泡都有较好的反映。基于传感器的这种结构,分析了油水经过传感器所表现的现象,发现了一种新的油水含水率检测机理。借助有关理论建立了一种新的同轴电容含水率计理论模型。
由于6个同轴电容器是并联关系,任取其一进行分析,其结构示意图见图1。

图1 同轴电容器结构示意图
设同轴电容器中心电极的半径为r,包裹电极的绝缘层外半径为r1,绝缘材料的相对介电常数为εr1,外电极内半径为r2,绝缘层与外电极之间的流体介质的介电常数为εr2,传感器高度为H。则电容器的电容为
(1)
根据上述同轴电容含水率计油水检测机理,在泡状流前提下,每当有一个油泡经过同轴电容传感器时,其内电极绝缘介质上都会形成一定厚度的滞留层油膜,油水以同轴层状分布。
由于在测量频率小于10 kHz时水可看作是良导体,此时,式(1)可以写成
(2)
式中,r*为滞留层油膜外边缘到內电极中心的距离,即等效外电极内径。
设含水率从100%~0对应于有相应份数的油泡和水泡,每一份油泡和水泡的体积都相同。当一份油泡流过传感器时,会在测量电极表面填充一定厚度的滞留油膜,而其余99份水流过传感器时,必然会在测量电极表面减少一定厚度的油膜,增减油膜依指数规律。又设任一含水率为fw时1-fw份油泡给测量电极充填的滞留层厚度至h2,fw份水使测量电极上的滞留油膜厚度减少至h1,两电极间距为R,传感器充油膜系数为k1(与传感器结构、材料、油黏度、温度有关),减油膜系数为k2(与传感器结构、油黏度、温度有关),流量系数为Q,则
充油膜时,有方程
(3)
减油膜时,有方程
(4)
联立式(3)和式(4),解得
(5)
(6)
含水率为fw期间滞留层油膜的有效厚度为
(7)
将式(7)带入式(2),得到同轴电容器的电容与油水混合介质含水率的关系
(8)
对同轴电容传感器电容的测量是通过一个555振荡电路,将电容的变化转变为振荡输出信号的频率变化来实现的。它们之间的关系为
(9)
式中,R1和R2分别为振荡电路中的2个电阻参数;c为同轴电容传感器的电容。将式(9)带入式(8),整理得
(10)
令
(11)
(12)
R=r2-r1
(13)
将式(11)、式(12)与式(7)一起带入式(10)并整理得
(14)
可以看出,同轴电容传感器的振荡频率与流体含水率之间为复杂对数关系。
1.2 模型参数变化对信号输出响应的分析
在传感器的结构已确定情况下,模型中电路输出信号频率与流体流量、增膜因子和减膜因子有关。
(1) 流量变化的影响。在k1、k2不变情况下,让流体流量从1 m3/d增加到4 m3/d,数值模拟结果见图2。可以看出,随流量的增加,输出响应频率下降,曲线弯曲部分曲率变小。

图2 流量变化对响应的影响
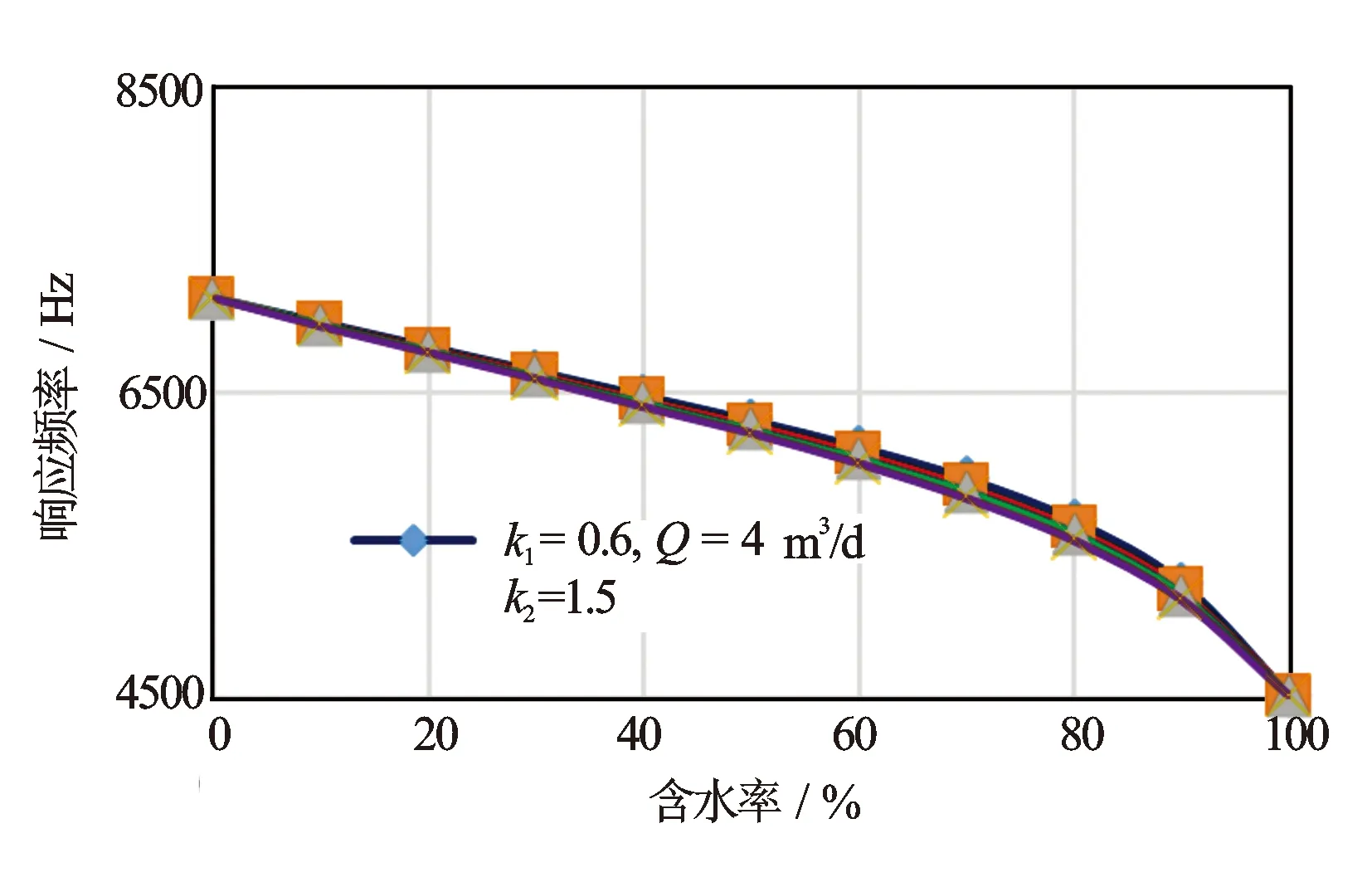
图3 增膜因子变化的影响
(2) 增膜因子变化的影响。在流量和减膜因子不变的情况下,增膜因子从0.6增加到0.75,数值模拟结果见图3。可以看出,增膜因子影响曲线曲率变化大的部分,且随因子的增大输出响应频率减小,曲线曲率变小。

图4 减膜因子变化的影响
(3) 减膜因子变化的影响。在流量和增膜因子不变的情况下,减膜因子从1.4增加到1.7,数值模拟结果见图4。可以看出,减膜因子影响曲线曲率变化大的部分,且随因子的增大输出响应频率增大,曲线曲率变大。
从以上模型的推导和分析看,模型是基于流过传感器的不同含水率的油泡在传感器测量电极上增加滞留层厚度而水泡减少其厚度的机理来测量含水率,同时模型建立过程中考虑了流体流量和温度、油黏度以及传感器结构等因素。所以,所建模型为一种同轴电容含水率传感器的新的理论模型。
2 低流量下同轴电容含水率传感器模型验证
2.1 低流量下同轴阵列电容含水率传感器特性实验研究
2.1.1 实验系统
实验在两相流模拟系统中进行(见图5)。其中的油相和水相流量分别由球阀开关控制,流量读数由玻璃浮子流量计指示。2种规格的浮子流量计LZB-15和LZB-25的工作温度都是20 ℃,可控制水流量变化范围0.24~24 m3/d。实验前,预先对玻璃浮子流量计的刻度进行油相和水相刻度。实验中采用的介质为自来水和15号工业白油。实验在室温条件下进行。

图5 油水两相流模拟系统
2.1.2 实验方案
同轴阵列电容含水率传感器的含水率动态测量实验中,流量大致按1、2、4、6、8、10、15 m3/d和20 m3/d设计。根据实验系统条件,尽量将含水率测点控制在0~100%范围内普遍分布,并适当加密高含水段(80%~100%)测点数。对应于每一个给出流量,含水率测点尽量最多。
2.1.3 实验结果
根据实验方案,在垂直模拟井中分别测量了给定流量下对应于系统提供的不同含水率下同轴阵列电容传感器的输出频率值,并将不同流量下测得的传感器响应频率与含水率间的关系进行整理,得到图6所示的关系曲线图。

图6 同轴阵列电容含水率传感器动态实验结果
可以看出,在低流量下,对于每一个流量,同轴阵列电容传感器在0~100%含水率变化范围内的响应频率与含水率间呈复杂的对数函数关系,全程都有较好的分辨率,特别是在含水率大于90%的高含水阶段分辨率尤其突出。表明研制的阵列电容含水率传感器不仅适合0~100%范围内的含水率测量,更适合高含水情况下的含水率测量。同时也表明,流体的流量对实验结果有很大影响,随着流量的增大,传感器响应频率下降,特性曲线的弯曲部分的曲率变小,这一实验结果与新建的同轴电容含水率理论模型的分析结果相一致。图6中流量分别为8、10、15 m3/d和20 m3/d的曲线不完整,是受实验模拟仿真系统条件所限的结果。
2.2 同轴电容含水率传感器数值模拟
为了检验建立的理论模型的正确性,根据实验所采用的流量和含水率条件优化出模型中的流量系数、增膜系数和减膜系数后对模型进行了数值模拟,其结果见图7。去除模拟井筒在高含油阶段油水出现带水或交换情况明显外,对于实验中含水率大于50%的情况,理论曲线与实际测量曲线吻合较好,从而验证了所建的同轴电容含水率理论模型是正确的。
2.3 同轴电容含水率模型求解与精度评价
采用牛顿迭代法对测量模型进行求解,可以得到对应于各测量频率下的含水率的值,其迭代方程为
(12)
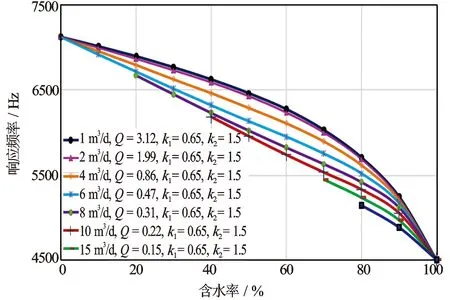
图7 模型在实验条件下的输出响应数值模拟
其中,
对实验测量数据进行插值,得到含水率分别为0%、10%、20%、30%、40%、50%、60%、70%、80%、90%、100%各点对应的响应频率。将各点频率值带入迭代式进行迭代,得到由理论模型计算给出的所有测点的含水率值见表1。
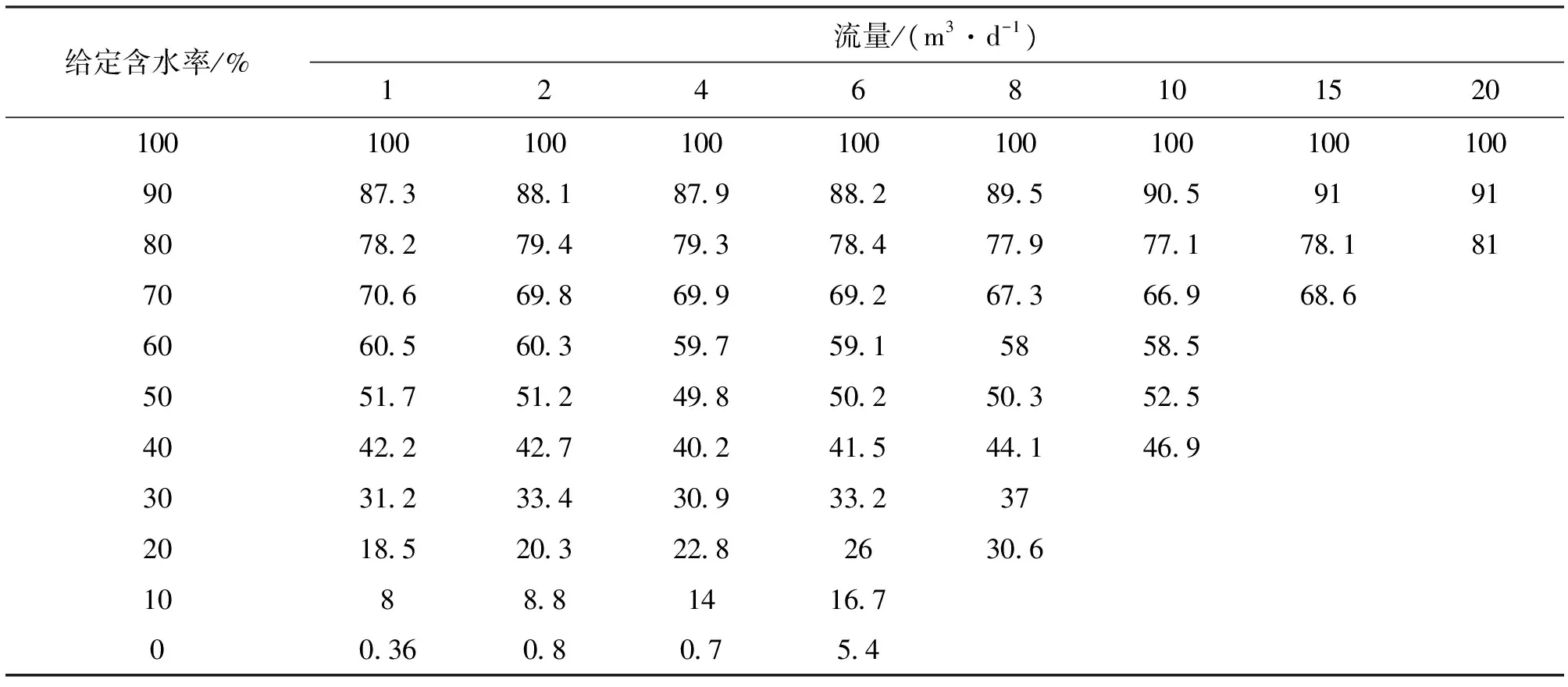
表1 由测量模型计算得到的含水率数值表
通过对模型在各测量点的含水率计算可以看出,实验获得的含水率数据与理论模型计算得到的含水率的绝对误差比较小,特别是在含水率大于50%情况下更小。同一流量下含水率越低得到的含水率标准差越大;同一含水率下流量越高得到的含水率标准差越大。所有测点的含水率标准差为2.7%,含水率大于50%的所有测点的标准差为1.41%。由于在模拟生产条件下进行的实验,含水率在低含水阶段出现带水或油水交换现象,结果表现为传感器输出响应频率降低。而建立模型时没有考虑此种情况。综合以上分析,在含水率大于50%的情况下,所建立的同轴阵列电容含水率理论模型具有更高的精度。
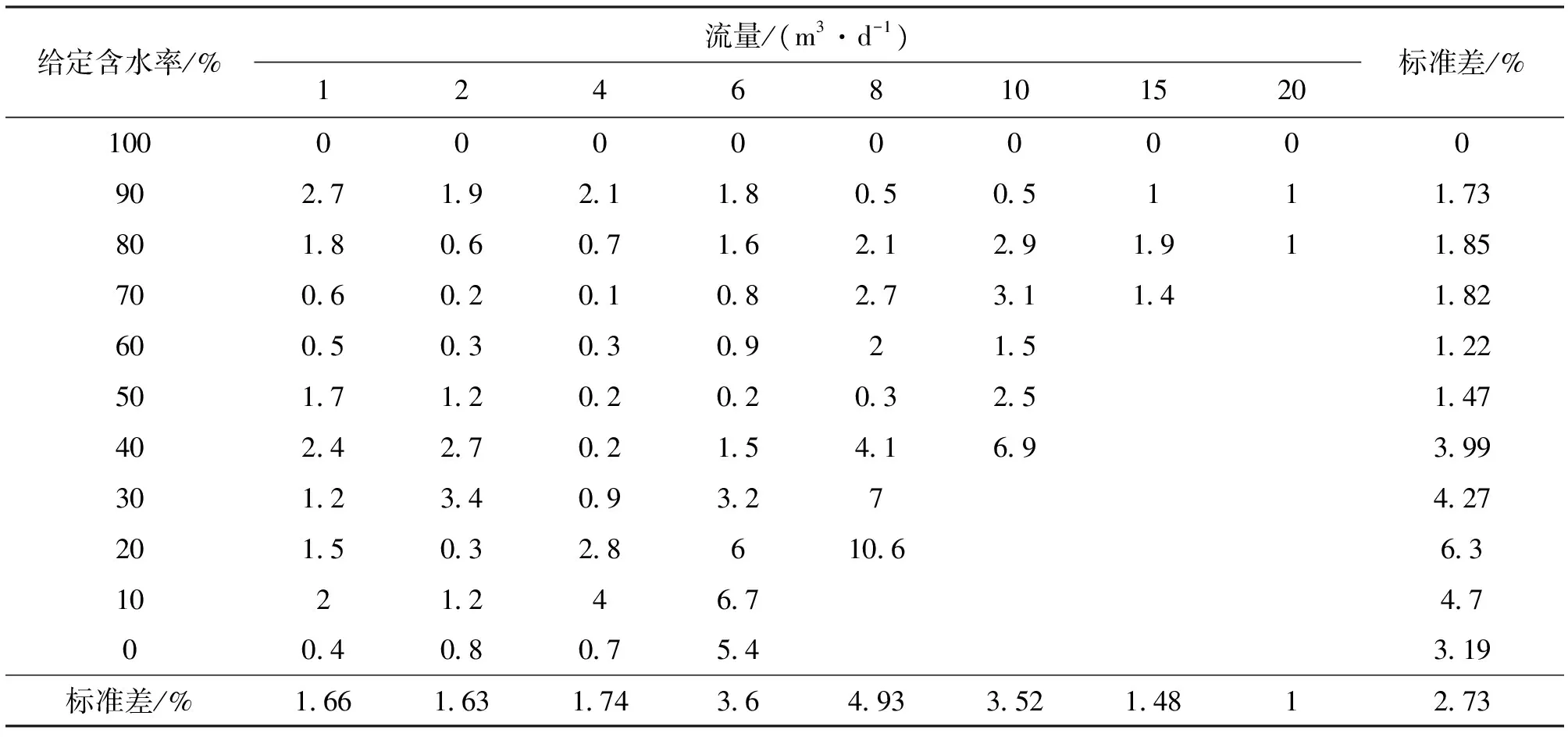
表2 各测量点含水率绝对误差和相同流量和含水率的标准差数值表
3 结 论
(1) 由同轴阵列电容含水率传感器理论模型建立和评价各方面可以得出同轴电容器內电极绝缘层上油相介质滞留层厚度是按指数规律增减的,且具有一般性。
(2) 同轴阵列电容含水率传感器的理论模型揭示了电路响应频率与含水率间为复杂的对数关系。
(3) 同轴阵列电容含水率传感器的理论模型考虑了流体流量、传感器结构、流体黏度、温度等影响,没有考虑模拟生产条件下含水率在低含水阶段出现带水或油水交换情况,在含水率较低范围实验与模型计算误差较大,但在含水率大于50%情况下与实验吻合很好,表明所建理论模型具有高含水适用性。
参考文献:
[1] BURRUS B. Determination of Oil Water Volumes by the Capacitance Method [C]∥SPE,1373.
[2] CARLSON N R,BARNETTE J C,DAVARZANI M J. Application of the Fluid Capacitance Log in Multiphase Flows [C]∥Formation Evalution Symposium,1986,22-25.
[3] JIN Z W,GUO H M,WU X L. New Response Equations of Fluid Capacitance Instrument and Application in Muitiphase Flows [C]∥SPWLA 31st Annual Logging Sysmposium,1990,P24-27.
[4] 吴锡令,赵亮. 油井中混合流体的电特性模型 [J]. 测井技术,1998,22(5): 318-320.
[5] 贾修信. 电容法测量含水率原理及其应用的探讨 [J]. 测井技术,1985,9(6): 73-80.
[6] LIU X B,QIANG X F,QIAO H T,et al. A Theoretical Model for a Capacitance Tool and Its Application to Production Logging [J]. Flow Measurement and Instrumentation,1998,9: 249-257.
[7] ZHANG H J,QIAO Q T,LIU X B. A New Measurement Principle of a Fluid Capacitance Sensor for Measuring Water Cut in Oil-water Mixtures [J]. The Log Analyst,1997: 30-35.
[8] 于宝,于靖民,陈钰,等. 低流量下同轴阵列电容法测量含水率实验研究 [J]. 测井技术,2012,36(6): 559-563.
[9] 周光坰,严宗毅,许世雄,等. 流体力学下册 [M]. 2版. 北京: 高等教育出版社,2000.
