测井仪外壳体强度蒙特卡罗模拟分析

2017-05-08林坤马朝选董强黄亚彭晓光

测井技术 2017年1期

关键词：蒙特卡罗外壳壳体

林坤,马朝选,董强,黄亚,彭晓光

(中国船舶重工集团公司第七一八研究所,河北邯郸 056027)

0 引言

石油测井仪器的工作环境极其恶劣。随着测井深度的增加,温度不断升高,压力也不断加大。在井下深度至7 000 m时,温度会达到175 ℃,压力也会达到140 MPa,仪器外壳体承受的压力不断增大。

随着钻井的井眼直径越来越小,测井仪器的外径越来越小,在满足外部压力的条件下,外壳体的壁厚越小,内径就越大,外壳体内部就有较大的空间布置电路和探测器。

在文献[1]和[2]中,应用传统的设计方法以及力学的第三和第四强度理论进行测井仪外壳的强度设计与校核,为计算测井仪外壳体壁厚及强度校核提供了理论依据,但安全系数的选择如果不合适的话,都会造成对仪器外壳强度的影响。同时,在测井仪外壳设计好后,生产加工好后进行压力试验,如果不满足要求,再重新设计,这样测井仪外壳的设计生产周期大大延长,导致时间和成本上升。

本文应用有限元分析ANSYS软件的结构分析模块与可靠性分析模块PDS(Probability Design System)相结合,采用Monte-Carlo蒙特卡罗法,以四探头高精度自然伽马测井仪壳体壁厚、压力载荷及材料的弹性模量等作为随机输入变量,对外壳体的蒙特卡罗模拟并进行分析,得出不确定设计因素与目标变量的灵敏度关系,影响强度的主要影响因素和壳体的可靠度,为结构可靠性优化设计提供有用数据,减少试验时间,提高设计效率。

1 外壳体应力-强度模型

机械结构的破坏概率可以表示为

Pf=P{g(X)<0}

(1)

式中,X={x1,x2,…,xn}为具有n维随机变量的向量;g(X)为结构的极限状态方程。

机械结构可靠性研究的主要对象是结构的强度R与应力S,通过研究两者之间的功能函数确定机械结构的可靠性。由此得到的结构功能函数可以表述为应力-强度模型

Z=R-S

(3)

概率极限状态结构设计中必须满足条件(4)

Z=g(R,S)=R-S≥0

(4)

根据应力强度干涉理论,在四探头高精度自然伽马测井仪外壳结构的使用过程中,不允许出现应力超过屈服强度的事件发生,所以外壳结构失效的准则为

σmax≥σs

(5)

式中,σmax为外壳结构在工作中出现的最大应力;σs为外壳材料的屈服强度。于是应力-强度模型为

Z=g(X)=σs-σmax≥0

(6)

蒙特卡罗法又称为随机模拟法或统计试验法[3],将随机变量xi代入功能函数g(x),得出一个函数值g(xi)。若g(xi)<0,则在计算机程序中记入一次失效的实现;若g(x)>0,则不记入。这样就完成了一次计算,再产生下一个随机数,重复上面的计算,直至完成预定的实验次数为止。用蒙特卡罗方法表示的失效概率可以表示为

(7)

式中,N为抽样模拟总数;当g(xi)<0,I[g(xi)]=1,反之,I[g(xi)]=0。

2 基于ANSYS/PDS外壳体强度蒙特卡罗模拟

四探头高精度自然伽马测井仪外壳体初步设计参数:承受外部压强140 MPa;外壳体长度3 000 mm;壳体外径45 mm;壳体内径35 mm。外壳体的材料采用一种超高强度钛合金TC11,屈服点为σs=1 030 MPa,并采用一定的热处理工艺,达到高强度。

应用ANSYS软件中PDS(Probability Design System)概率设计模块对该测井仪外壳体结构进行蒙特卡罗模拟与可靠性分析。

2.1 生成分析文件

该阶段包括对输入参数进行参数化设定,模型的建立、网格划分,加载求解和后处理[4-6]。

(1) 定义输入参数。输入参数主要是指影响结构行为的不确定因素如材质的不确定性,结构几何尺寸的不确定性等,输入的相关参数见表1。

表1 输入参数表

(2) 建立模型。本文采用图形用户接口GUI方式,用自下而上的方法建立外壳体模型,通过创建关键点、线,建立立柱截面,然后通过拉伸、镜像、布尔运算等命令,生成了外壳体的参数化有限元模型。

(3) 网格的划分。有限元模型采用SOLID92单元,并设定轴对称选项,建立1/2轴对称分析模型。用SizeControl对网格单元的大小进行了控制,用volume sweep(体扫描)的方式对立柱进行了网格划分。

(4) 加载并求解。壳体外壁施加均匀压力面载荷,壳体XOZ平面施加固定约束。加载和约束后的有限元模型见图1。

图1 施加约束后的外壳体有限元模型

(5) 后处理。求解后,提取外壳体的Y向最大变形和最大等效应力作为后续结构可靠性分析的输出参数。

2.2 外壳体蒙特卡罗模拟

采用蒙特卡罗法[7-8],循环次数初选loop=500,输入参数的分布类型如表2所示,进行蒙特卡罗模拟并输出结果。

表2 输入变量概率分布类型及参数

3 外壳体蒙特卡罗模拟结果分析

3.1 统计结果分析

选择了工作压力p、壁厚H这2个具有代表性的变量,观察其函数取值的分布,Y向最大变形和最大等效应力的均值变化曲线分别如图2和图3所示。中间的1条曲线表示函数的平均值,而上下2条曲线则表示了抽样过程中向平均值趋近的过程,曲线越接近,表明平均值越趋向于收敛。从图2和图3中可看出,Y向最大变形和最大等效应力的平均值均趋向收敛,说明本文采用500次循环模拟次数是足够的。

图2 UDMAX的均值变化曲线

从图2和图3中可得到Y向最大变形的平均值约为0.06 mm,标准差为0.008 mm,最大等效应力的平均值为845.6 MPa,标准差为38.25 MPa。

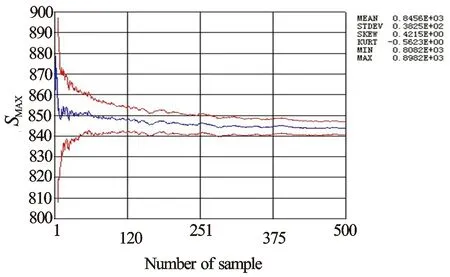
图3 最大等效应力SMAX的均值变化曲线

3.2 输出变量敏感性分析

输出变量敏感性分析结果见图4。其中,输入参数对输出参数影响水平在2.5%以下的归为相对影响不大的因素;影响水平在2.5%以上的归为有显著影响的因素。

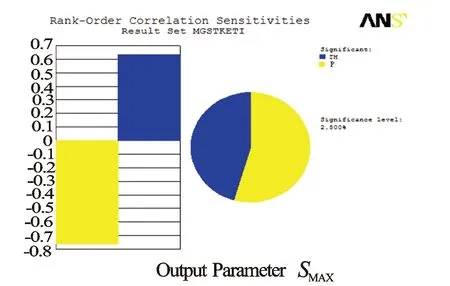
图4 敏感性分析结果示意图

从图4可以看出,压力载荷p是影响失效的最主要因素;其次是壳体厚度H。因此设计和制造过程中应严格控制这些参数。壳体的可靠度对压力载荷p的灵敏度为负值,表示压力载荷p增大,结构的等效应力最大值增加,其强度的可靠性降低。

在设计和制造时,应严格控制这些主要敏感参数。在经济成本允许的情况下,可考虑适当增加外壳体的厚度H,以改善外壳体的强度和刚度,使其获得更好的力学性能,保证外壳组件的承压强度。

3.3 结构可靠性分析

外壳体承受的最大压力为140 MPa,屈服强度为1 030 MPa,最大等效应力的平均值为845.6 MPa,标准差为38.25 MPa。因此,运用“pdprob”命令计算外壳体的最大等效应力SMAX小于1 030 MPa的概率,在置信度为95%的情形下,最大等效应力的可靠度均为100%。说明外壳体采用初步设计参数的结构可靠,安全度高。

对四探头自然伽马测井仪外壳体做外压密封试验,在140 MPa压力下,保持15 min,要求无塑性变形及泄露。压力试验结果表明,外壳体加压、保压、卸压正常,验证了初步设计的正确性。