重型商用车钢板弹簧悬架硬点优化设计

易晨阳张瑞亮陈澔利刘维达

（1.太原理工大学，太原 030024；2.大运汽车制造有限公司，运城 044000）

重型商用车钢板弹簧悬架硬点优化设计

易晨阳1张瑞亮1陈澔利2刘维达1

（1.太原理工大学，太原 030024；2.大运汽车制造有限公司，运城 044000）

利用Adams/Car对某重型商用车钢板弹簧前悬架进行建模及运动学特性仿真。针对仿真中出现的前束角和主销后倾角变化过大的问题，结合钢板弹簧结构特性进行分析，提出了悬架硬点设计变量的初选方案。采用灵敏度分析方法确定设计变量，通过响应面法对目标函数进行拟合，结合多目标遗传优化算法NSGA-Ⅱ对悬架硬点坐标进行了优化。结果表明，前束角和主销后倾角的变化分别减少了72.2%、68.2%，钢板弹簧悬架运动学特性明显的改善。

1 前言

钢板弹簧悬架是目前商用车应用最为广泛的悬架类型，其运动学特性与独立悬架有较大的差别。悬架硬点布置决定了悬架运动学特性（Kinematics，简称K特性），即车轮定位参数在车轮跳动和转向时的变化特性，它对车辆的操纵稳定性以及轮胎的磨损都有着直接的影响[1]。合理的硬点坐标对于改善悬架性能有着重要意义。文献[2]采用牛顿迭代法对麦弗逊悬架的硬点坐标进行了优化；文献[3]、文献[4]分别采用目标规范法和多次迭代修改方法，以双横臂悬架的硬点坐标为设计变量，对悬架运动学特性进行了优化设计，改善了车辆的操纵稳定性；文献[5]通过对双横臂扭杆式独立悬架的硬点坐标进行优化匹配，改善了前束角和外倾角变化特性，减轻了轮胎磨损；文献[6]、文献[7]采用响应面法拟合目标函数，分别对双横臂悬架和多连杆悬架硬点进行了优化，相比其他方法，优化效率明显提高。本文以某重型商用车钢板弹簧前悬架为研究对象，利用Adams/Car建立其多体动力学模型，并分析了该悬架定位参数随车轮跳动的变化情况，在文献[7]的优化方法基础上，结合钢板弹簧悬架的运动学特性，采用了更高效的NSGA-Ⅱ遗传算法，建立了从硬点初选、灵敏度分析、目标函数响应面法拟合到NSGA-Ⅱ多目标优化的完整优化设计流程，对悬架硬点坐标进行优化设计，改善了悬架性能。

2 钢板弹簧前悬架模型的建立

钢板弹簧前悬架模型由钢板弹簧子系统、转向机构子系统和转向悬架子系统组成。钢板弹簧前悬架的设计硬点名称及坐标如表1所示。

表1 钢板弹簧前悬架设计硬点坐标 mm

2.1 钢板弹簧子系统建模

钢板弹簧不同于其他悬架弹性单元，其不但具有承载功能，还具有导向功能和一定的减振作用。钢板弹簧的导向作用对于悬架运动学特性有着直接的影响。因此，应用于悬架运动学特性仿真的钢板弹簧模型的简化过程不能只考虑其刚度特性。本文采用离散梁方法[8]建模。钢板弹簧子系统共3个设计硬点（对称位置记左侧坐标），其坐标值见表1中的第1点～第3点。

2.2 转向机构子系统建模

利用Adams/Car建立的转向机构子系统包括转向盘、转向管柱、转向轴、转向传动轴、转向器输入轴、转向器、转向摇臂、转向直拉杆和转向节臂。转向机构子系统共8个设计硬点，其坐标值见表1中的第4点～第11点。

2.3 转向悬架子系统建模

按照Adams/Car中的子系统划分方法，将前悬架中的转向桥与减振器划入转向悬架子系统。根据目标车辆实际结构进行适当简化，建立的转向悬架子系统模型具体包括减振器、前桥、转向梯形臂、转向横拉杆和转向节。转向悬架子系统共10个设计硬点，其坐标值见于表1中的第12点～第21点。

将上述3个子系统与Adams/Car中的悬架试验台进行装配，并根据实车数据设置试验台相关参数（见表2），得到图1所示的钢板弹簧前悬架模型。

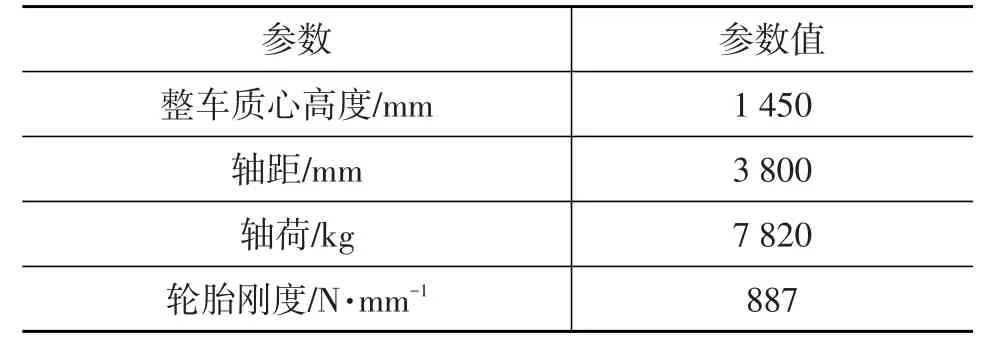
表2 悬架试验台参数

图1 钢板弹簧前悬架模型

3 悬架运动学特性仿真分析

商用车总质量一般较大，特别是重型商用车，轴荷普遍达到数吨。目前，国内现有的悬架K&C特性试验台主要用于轴荷较小的乘用车悬架特性测试，不能满足重型商用车悬架特性的测试要求。因此，采用试验方法获得悬架运动学特性存在诸多困难。Adams软件中可以建立精确的悬架模型，并通过专业的悬架测试模块分析悬架的运动学特性，成为获取重型商用车悬架运动学特性分析的有效途径。

3.1 仿真设计

车轮平行跳动引起的前束角、车轮外倾角、主销内倾角和主销后倾角等4个定位参数的变化是分析悬架运动是否合理的重要依据，可以较为全面地反映悬架的运动学特性。平行轮跳仿真的主要参数设置为：车轮跳动高度范围为-60～60 mm，仿真步数为100，仿真模式为运动学（Kinematic）模式。

3.2 悬架运动学特性分析

各定位参数设计值如表3所示，定位参数随车轮跳动的变化曲线如图2所示。

表3 车轮定位参数设计值 （°）

图2 定位参数与车轮跳动量的关系

由仿真结果可以看出，车轮外倾角和主销内倾角随车轮跳动的变化较小，满足设计要求。前束角和主销后倾角随车轮跳动的变化较大，会导致车辆行驶稳定性恶化、轮胎磨损异常，因此需要进一步优化。

3.3 悬架硬点的初选

根据前束角、车轮外倾角、主销内倾角和主销后倾角等4个定位参数随车轮跳动的变化特性，结合钢板弹簧悬架的结构特性和使用工况，对定位参数变化的原因及与其相关的悬架硬点进行分析，并进行悬架硬点的初选。

前束角随车轮跳动而产生变化的主要原因是悬架系统导向机构与转向系统的垂直运动和横摆运动的互相干涉。本文所建立的钢板弹簧悬架模型中未加装其他导向杆系，因此主要由钢板弹簧起导向作用。钢板弹簧的刚度特性、几何特性以及安装位置都对其导向性能有直接的影响。在尽量不影响悬架承载性能的前提下，考虑选择钢板弹簧安装位置硬点坐标在合理的范围内进行优化，是减小前束角变化较为合理的途径。因此，选出钢板弹簧前端与车架连接位置、吊耳与车架连接位置、钢板弹簧后端与吊耳连接位置和钢板弹簧在前桥上安装位置共4个硬点（硬点序号分别为1、2、3和11）。转向系统考虑有空间运动而非绕自身轴线旋转的杆件，同时不能影响各定位参数初始值，初步确定转向节臂与转向直拉杆连接位置和转向横拉杆与转向梯形臂连接位置共2个硬点（硬点序号分别为8和17）。

主销后倾角随车轮跳动而产生变化的主要原因是悬架系统导向机构与转向系统的垂直运动和俯仰运动的互相干涉。考虑到钢板弹簧悬架的主销真实存在且与刚性前桥固定，两者在主销后倾角变化方向上没有相对运动。由此推断是由于钢板弹簧在车轮跳动时的不正常运动特性和变形特性导致前桥出现俯仰运动，带动主销运动，使得主销后倾角发生变化。因此，钢板弹簧安装位置硬点坐标也是主销后倾角变化的主要原因。

主销内倾角随车轮跳动几乎不发生变化是由于主销与刚性车桥固定，车桥不存在弯曲变形，使得主销内倾角可以得到较好的保持。在不改变前桥与主销相关硬点的情况下，其他硬点的变动对主销内倾角影响非常小。

由于钢板弹簧悬架是非独立悬架，车轮通过车桥刚性连接，在不考虑车桥弯曲变形的情况下，车轮外倾角的变化主要是主销后倾角和前束角共同作用导致的，当主销后倾角不为0°时，前束角的变化（相当于车轮转向运动）会导致车轮外倾角的变化[9]，在主销后倾角较小的情况下，这种变化也相当有限。

综合上述分析结论，初步选出共6个相关硬点，分别为表1中序号为1、2、3、8、11和17的硬点。

4 悬架硬点优化设计

4.1 灵敏度分析

通过进行灵敏度分析，可以得出各设计因素对目标函数的影响大小，进而选择出合理的因素进行优化设计，提高优化工作的效率。

以平行轮跳仿真为基础，前束角和主销后倾角随车轮跳动变化量大小为响应函数，对初选的6个相关悬架硬点x、y、z向坐标参数共18个变量进行灵敏度分析。各硬点坐标的扰动范围设置为-10～10 mm。通过正交试验法进行了2水平筛选法仿真，共进行48次仿真。最终得出了各硬点坐标对前束角和主销后倾角随车轮跳动的变化量的影响大小，如表4所示。

表4 灵敏度分析结果

为了提高前束角和主销后倾角的优化效率，根据灵敏度分析结果，将对前束角或主销后倾角的影响大于10%的变量选出。由表4可知：硬点坐标leaf_to_frame.z和 steer_arm.z对前束角的影响较大；硬点坐标leaf_to_frame.z、leaf_to_shackle.x和leaf_to_frame.x对主销后倾角的影响较大。因此考虑选取上述4个硬点的坐标作为优化变量，分别记为x1、x2、x3、x4。

4.2 目标函数的响应面法拟合

根据灵敏度分析的结果，选取上述4个优化变量，利用Adams/Insight分别对前束角和主销后倾角2个目标函数进行拟合。仿真策略采用响应面法（DOE Response Surface），选择二次模型进行拟合，采用拉丁超立方（Latin Hypercube）设计方法，共进行100次仿真。

前束角拟合函数结果为：

主销后倾角拟合函数结果为：

通过拟合优度（Goodness-of-fit）检查拟合效果，2次拟合的各项指标值如表5所示。其中，可决系数R2越接近1，说明拟合优度越高，对于较好的拟合，R2通常大于0.9；修正可决系数R2adj越接近1也说明拟合效果越好；P值反映拟合项的显著性，它越小说明拟合效果越好，一般要求P值小于0.02；R/V为模型的计算值与原始数据点之间的关系，该值越大说明拟合结果可信度越高，一般要求R/V大于10。从表5可以看出，拟合效果比较理想。

表5 拟合优度指标结果

4.3 基于NSGA-Ⅱ算法的多目标优化

带精英策略的快速非支配排序遗传算法（NSGA-Ⅱ）是目前应用最广泛也是最优秀的多目标优化算法之一，其具有运行速度快、收敛性好、Pareto最优解集分布均匀等特点。

根据目标函数的响应面法拟合结果，建立多目标优化模型为：

式中，xio为xi的原始值。

设置种群大小为200，最优前端个体系数为0.2，交叉概率为0.8，变异概率为0.1，进化代数为500。经过计算得到Pareto最优解集如图3所示。

图3 Pareto最优解集分布

由图3可知，目标函数fΔtoe和fΔcas之间存在冲突，从综合性能的角度考虑，选取中间段的Pareto最优解较为合适。考虑到对变量参数的改动应尽量小，从而不影响悬架的其他性能，在中间段几个相近解中选择本次优化的最终解，其对应的优化变量取值对比如表6所示。

表6 悬架硬点坐标优化结果 mm

按照优化后的硬点坐标对原钢板弹簧前悬架模型进行修改，对优化后的悬架在相同工况下进行仿真。优化前、后车轮定位参数随车轮跳动的变化曲线对比如图4所示。

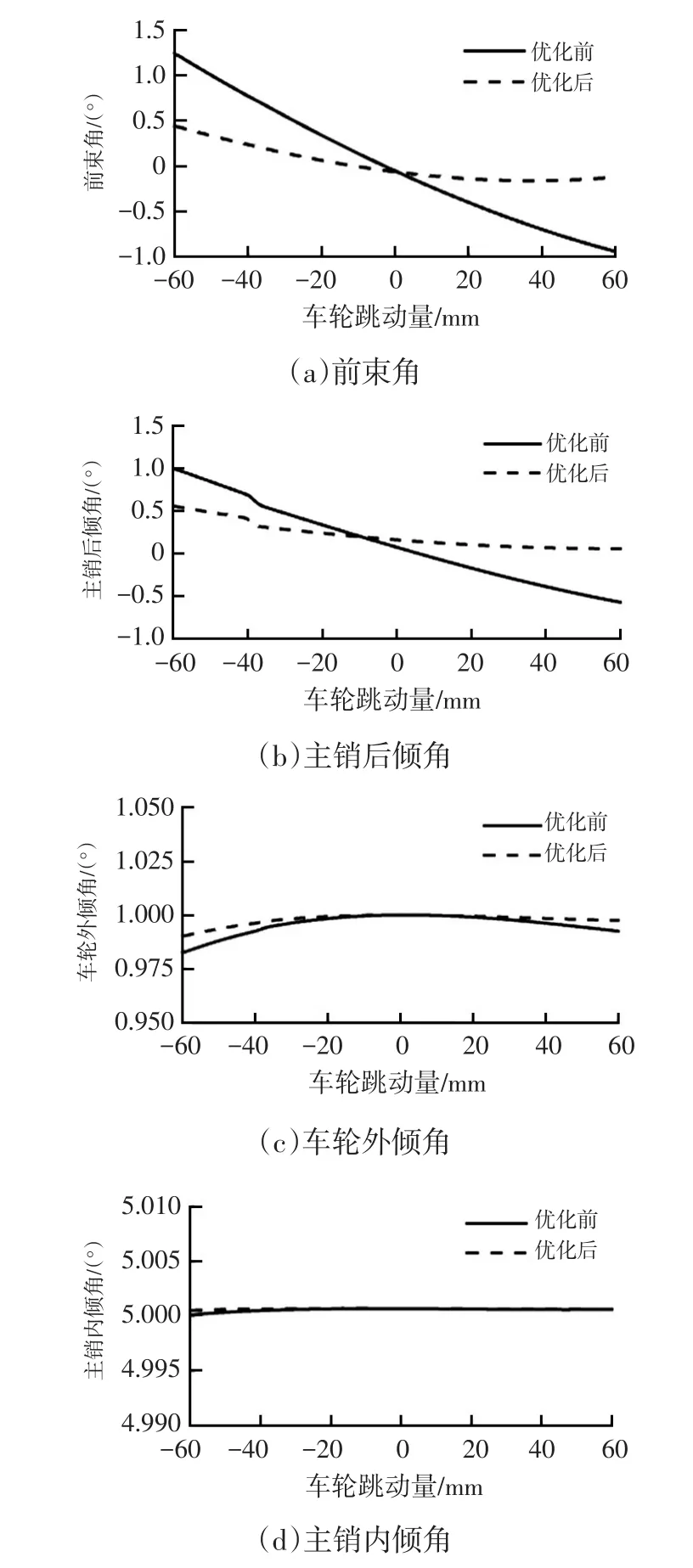
图4 优化前、后定位参数与车轮跳动量的关系

5 结论

通过Adams/Car建立了某商用车钢板弹簧前悬架多体动力学模型。通过平行轮跳仿真对其悬架运动学特性进行了仿真，并根据仿真结果，结合钢板弹簧悬架的结构特性，对定位参数变化的原因及与其相关的悬架硬点进行分析，为悬架硬点的初选提供了指导。

通过Adams/Insight对初选的硬点坐标进行灵敏度分析，确定了影响最大的4个硬点坐标为最终的优化变量。运用响应面法对目标函数进行拟合，并检验了拟合优度，确定了多目标优化模型。基于该模型，通过NSGA-Ⅱ算法进行了多目标优化，得到了前束角和主销后倾角变化的两目标Pareto最优解集。该方法提高了多目标优化的效率，并为工程设计人员提供了灵活的设计空间选择。

最后，选择出最优解验证了优化效果。通过对钢板弹簧悬架硬点的优化，悬架运动学特性显著改善，对于改善车辆操纵稳定性、减小轮胎磨损有重要意义。

1 石琴.前悬架K&C特性优化设计及整车操纵稳定性分析.合肥：合肥工业大学，2012.

2 廖永升，刘拥军，陈璟，等.基于ADAMS的麦弗逊悬架运动学优化.科学技术与工程，2012（20）：4935～4940+4950.

3 丁亚康，翟润国，井绪文.基于ADAMS/INSIGHT的汽车悬架定位参数优化设计.汽车技术，2011（5）：33～36.

4 向铁明，沈理真.基于ADAMS的某赛车前悬架杆系优化.汽车工程，2014（4）：486～490.

5 冯金芝，梁鹏，郑松林，等.扭力梁后悬架K&C特性仿真分析.现代制造工程，2015（10）：57～61.

6 唐应时，朱位宇，朱彪，等.基于轮胎磨损的悬架与转向系统硬点优化.汽车工程，2013（7）：640～644+653.

7 Topaç M M,Deryal U,Bahar E,et al.Optimal kinematic design of a multi-link steering system for a bus independent suspension: An application of response surface methodology.Mechanika，2015，21（5）：404～413.

8 李杰，朱毅杰，刘煜.钢板弹簧建模模块LeafSpring的研究及其应用.科学技术与工程，2011（30）：7555～7559+7569.

9 王霄锋.汽车悬架和转向系统设计.北京：清华大学出版社，2015.

（责任编辑 斛 畔）

修改稿收到日期为2016年11月9日。

Optimal Design of Leaf-Spring Suspension Hard-points for a Heavy Commercial Vehicle

Yi Chenyang1,Zhang Ruiliang1,Chen Haoli2,Liu Weida1
（1.Taiyuan University of Technology,Taiyuan 030024;2.Shanxi Dayun Automobile Manufacturing Co.,Ltd., Yuncheng 044000）

Modeling and kinematic properties simulation of leaf-spring front suspension for a heavy commercial vehicle was made with software Adams/Car.The simulation showed oversized changes of the toe angle and caster angle.To solve this problem,we analyzed leaf-spring structural characteristics,and proposed a primary program which set the suspension hard points as design variables.The design variables were determined by the method of sensitivity analysis,and the objective functions were fitted by response surface method,the suspension hard point coordinates were optimized by multi-objective genetic algorithm NSGA-Ⅱ method.The results showed that,the changes of toe angle and caster angle were reduced by 72.2%and 68.2%respectively,the leaf-spring suspension kinematic properties were improved dramatically.

Leaf-spring suspension,K&C characteristic,Hard-points coordinate,NSGA-II multi-objective optimization

钢板弹簧悬架 K&C特性 硬点坐标 NSGA-Ⅱ多目标优化

U467.1

A

1000-3703（2017）03-0033-05