数学核心素养评价的一个框架

喻 平



数学核心素养评价的一个框架

喻 平

（南京师范大学课程与教学研究所，江苏南京 210097）

学生数学核心素养的生成，源于对数学知识的学习．数学知识学习表现为3种形态：知识理解、知识迁移、知识创新．知识学习的3种形态生成不同水平的数学核心素养，因此，对数学核心素养形成的评价应当基于知识学习的3种形态．据此对数学核心素养分为3种不同水平，这种水平划分吸取了布卢姆模型、PISA模型的长处，又体现了数学学习的特征，具有理论性和可操作性双重特性．

数学核心素养；核心素养水平；知识理解；知识迁移；知识创新

在《教育部关于全面深化课程改革落实立德树人根本任务的意见》中，明确界定了核心素养，即学生应具备的适应终身发展和社会发展需要的必备品格和关键能力．目前，教育部正在组织专家对高中课程标准进行修订，要求把学科核心素养作为修订课程标准的主线，围绕学科核心素养制订教学内容、评价标准和教材编制．做这个工作应当有一些思考，正如郑毓信先生指出的：应当更为深入地研究与理解“核心素养”的具体涵义与现实意义，包括它与“素质教育”的联系与区别．从实践的角度看，不应唯一强调所谓的“整合课程”，乃至片面地提倡“去学科化”，而是应当更加重视如何能将这一思想落实于各个具体学科的教学之中[1]．

把学科核心素养渗透在课程中，面临两个必须解决的问题，一是确定学科核心素养的成分；二是确定学科核心素养的水平．目前，各学科对这两个问题都有了初步方案．高中数学课程标准修订组的专家提出了6种数学核心素养成分：数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析，并对每一种素养作了3个水平的划分．

现在的问题是，提出的6个数学核心素养成分是否合理、科学？每一个核心素养的水平划分的依据又是什么？这两个问题既有相互关联又具相对独立性，因为不论核心素养的成分是什么，对它们的水平划分应当有一个统一的标准和尺度．因此，这里绕过第一个问题，就数学核心素养的水平划分依据作一探讨．

1 几种学习评价模型分析

1.1 布卢姆模型

美国教育心理学家布卢姆（Bloom）的研究团队，在1950年代用分类学方法分析学生的学习目标，将其分为认知、情感和动作技能3个领域，每一领域的目标又由低级到高级分成若干层次[2]．

认知领域的目标从低到高分为6级：（1）知识：对先前学习过的材料的记忆．（2）领会：能把握材料的意义．可借助于3种形式来表征：一是转换，即用自己的话或用与原先表达方式不同的方式表达自己的思想；二是解释，即对一项信息加以说明或概述；三是推断，即估计将来的趋势．（3）运用：能将习得的材料应用于新的具体情境．（4）分析：能将整体材料分解成它的构成成分并理解组织结构．（5）综合：能将部分组成新的整体，产生新的模式和结构．（6）评价：对材料作价值判断的能力．

之后，克拉斯沃尔（Krathwohl）完成了情感领域的目标分类．依据价值内化（指由外在的学习转化为个人内在的兴趣、态度、价值等心理特质）的程度，从低到高分为5级：（1）接受（注意）：学生愿意注意特殊的现象或刺激，包括从意识到某一事物存在的简单注意到选择性注意．（2）反应：学生主动参与，包括默认、愿意反应及反应的满足．（3）价值化：学生将特殊的对象、现象或行为与一定的价值标准相联系．（4）组织：将许多不同的价值标准组合在一起，克服它们之间的矛盾、冲突，并开始建立内在一致的价值体系．（5）价值与价值体系的性格化：个人具有长时期控制自己的行为以致发展了性格化“生活方式”的价值体系．

布卢姆的学习评价模型具有一些明显的特点．其一，将学习评价分为3个领域，3个领域相对独立，有各自的水平划分标准．值得注意的是，布卢姆的学习评价理论，并不只是考察学生掌握知识的情况，在比较高的水平阶段，考察的本质上是知识学习之后形成的能力．其二，对于认知领域的评价，基本上是对知识学习不同结果的评价，即围绕知识学习开展的，与中国目前课程标准中的“知识与技能”、“过程与方法”相对应，只是把这两个要素作为认知领域中不同的水平来表述．对于情感领域的评价，是针对非智力因素开展的，与课程标准提出的三维目标中的“情感、态度与价值观”相对应．相比之下，布卢姆对评价目标有清晰的划分，两个目标指向明确，具有实践层面的可操作性，而中国课程标准提出的三维目标，将3者作为一种并列关系却又捆绑在一起，在实践中是难以操作和实现的．

当然，布卢姆模型也有一些问题，把目标的水平划分得过细，难免会有水平之间的交叉、重叠关系．同时，这个模型是超越学科的，即可用于所有学科，但事实上，每个学科都有自己的特殊性，一种统一的模式难以涵盖所有学科的特征．

1.2 PISA模型

PISA（Programme for International Students Assessment）是一个由经济合作与发展组织策划并组织的项目，用于评价临近义务教育末期（15周岁）学生的阅读素养、数学素养、科学素养．PISA的测评内容和测评框架都是基于“素养”这一概念提出来的．PISA将素养定义为：学生运用所学知识和技能，有效进行分析、推理、交流，在各种情境中解决和解释问题的能力[3]．

PISA的评价一般分为两个维度．2003年的评价结构为：第一个维度是领域：数学素养、科学素养、阅读素养；第二个维度是知识的掌握和运用，又分为内容维度、过程维度和情境维度．以数学素养评价为例，第一维度数学内容，包括空间和形状、变化和关系、数量、不确定性．第二维度解题过程：要求学生面对现实生活中的数学问题，首先把它们转换成数学形式，然后进行数学运算，再把结果运用到原来的问题并写出答案．这样学生就要完成一个多步骤的“数学化”过程．第三维度问题情境．数学问题设置在个人的、教育或职业的、公共的和科学的情境中．学生的数学成绩被分成6个等级水平，这6个水平代表了任务的难易程度．

2012年，PISA给出的数学素养模型包括三维度架构：一是情境维度即问题情境，指15岁学生可能面临的各种问题，具体包括个人生活的、职业的、社会性的、科学性的4种情境．二是内容维度即数学内容知识，包括变化和关系、空间和图形、数量、不确定性4大领域内容．三是过程维度即3种数学过程（表述、运用、评估）和7种数学基本能力（交流，数学化，表述，推理和论证，设计问题解决策略，运用符号的、正式的、技术的语言和运算，使用数学工具）[4]．

PISA模型的特点表现为，第一，以考察学生的基本素养为指向，所测评的“素养”并不局限于学校常规课程，而是取自更广泛的知识和技能领域．换言之，PISA不是一种以知识为取向的评价，而是以素养为取向的评价．第二，问题设置在情境中．个人情境与学生个人的日常活动直接相关；教育或职业的情境出现在学生的学校生活或工作环境中；社会情境要求学生更广泛地观察周边环境的某些方面；科学情境更加抽象，可能会涉及了解一个技术过程、理论情境或明确的数学问题．

应当说，PISA模型将学生的素养作为评价内容，把知识与现实密切结合，它的评价重点不在于检验学生是否很好地掌握了学校课程，而是评价学生是否做好了应对未来挑战的准备，体现出这一评价模式的特色和功能．但是也应当看到，PISA过分追求问题的情境化，有偏激的一面，比如，就数学素养来说，并不是能够解决一些现实问题就意味具备了数学素养，数学中更多的内容是没有现实背景的，具备洞察数学学科内部的规律的意识和能力，具备用数学思维方法去处理事物的能力，这些数学核心素养在PISA中是难以测量的．

1.3 SOLO模型

SOLO（Structure of the Observed Learning Outcome）分类理论是由澳大利亚教育心理学家彼格斯（Biggs）在1982年首创的一种学生学业水平分类方法[5]．SOLO原意为可观察的学习结果的结构．SOLO分类理论是基于学生对某一具体问题反应的分析，对学生解决问题时所达到的思维水平进行由低到高的5个基本结构层次的等级划分：前结构水平、单点结构水平、多点结构水平、关联结构水平、拓展抽象水平．如果将SOLO模型的“多点结构水平”分解为两种水平，便可以与PISA的水平划分对应[6]．

SOLO分类评价理论的思想源头是皮亚杰的发展阶段学说．皮亚杰认为思维或者智慧的发展是心理发展的核心，其发展阶段的最主要特点是：阶段出现的先后顺序固定不变，每一阶段都具有独特的结构．SOLO主要用于学生解决具体问题的评价，而且以知识的考察为评价重点，用知识点的组合运用水平界定评价水平，不是对学生能力进行全方位的测量，这是SOLO模型的特点．

2 数学核心素养评价的内涵

数学素养的研究起步较早，但对数学素养没有统一的界定[7~8]．对于数学核心素养而言，根据核心素养这个上位概念的定义，可以界定为：学生应具备的适应终身发展和社会发展需要的必备品格和关键的数学能力．这里主要讨论定义中的“关键能力”要素．高中数学课程标准修订组的专家提出了6种数学核心素养：数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析，本质上就是6种关键能力．因此，数学核心素养的评价就是对学生形成这6种数学核心能力的评价．

既然是讨论能力，必然要回到“能力”与“知识”的历史纷争．历史上有“形式教育”与“实质教育”两种理论，它们是对教育目标认识的两种相对立的教育理论．前者认为教育旨在使学生的官能或能力得到发展；后者认为教育的目的在于使学生获得知识和生活的必备技能．两种理论的本质是对知识与能力孰轻孰重的考量．形式教育与实质教育各执己见虽有历史时代的原因，但是这种割裂了知识与能力的作法毕竟存在很大缺陷．知识与能力有不可分割的内的联系，它们不是相互独立或相互排斥的．事实上，作为实质教育的推崇者，斯宾塞（Spencer）本人也看到了知识的价值和训练的价值，他说“我们可以肯定，在获得那些调节行为最有用的各类知识中就包含了最适宜于增强能力的心智练习”[9]．20世纪初，许多教育家对形式教育和实质教育的极端观点作了批判．克拉夫基（Klafki）认为，学生不掌握内容如何促使能力发展呢？事实上，掌握内容本身也是一种能力[10]．

事实上，关于知识与能力的关系，信息加工心理学给出了更加彻底的描述．按照这种对知识的广义分类，传统意义上的知识对应于陈述性知识，技能对应程序性知识．将技能进一步分解为两个亚类：一类用于对外办事（通过练习可以达到相对自动化），一类用于对内调控（受个体意识控制），就与加涅（Gagne）把学习结果分为言语信息、智慧技能、认知策略产生了对应[11]：言语信息对应陈述性知识，智慧技能对应能相对自动化的程序性知识，认知策略对应受意识控制的程序性知识．显然，如果智慧技能的成分对应于技能，那么认知策略的成分则表现为能力．于是，认知心理学把能力作为知识的一种形式，使知识与能力得到统一．

以上讨论说明3个问题，其一，知识是能力产生的本源，知识也就是数学核心素养生成的本源；其二，数学核心素养的评价不能脱离对知识的评价；其三，数学核心素养的评价又不等同于对知识的评价，重点是对由知识学习转化而来的能力的评价．

3 数学核心素养水平划分的依据

要评价学生在6种数学核心素养的发展情况，必然要对这些核心素养进行水平划分．高中课标修订组的专家给出了每种核心素养的水平划分，但有两个问题值得商榷．第一，这种划分是针对高中学生3种不同层次的要求界定的，即分为高中毕业水平、高考水平、拓展水平（即准备参加高校自主招生的学生要达到的水平）．显然，这种水平划分对日常的学习评价没有直接的指导意义．第二，分为3种水平缺乏依据，即缺少应然说理．

既然数学核心素养产生于知识，那么评价的水平划分就应当从知识的角度切入，参照布卢姆模型、PISA模型和SOLO模型，提出如下一种数学核心素养划分的理论构想：将知识学习分为3种形态，由此产生的3种能力水平即为核心素养的3种水平．知识学习的3种形态依次为知识理解、知识迁移和知识创新，这3种形态本质上也反映了数学知识学习的3种水平．

3.1 知识理解

知识理解的第一层涵义，是指学习者对知识的本质、类属以及与其它知识之间的种种联系的理解．知识的理解既是一个过程，即学习者利用已有经验和已学过的知识去同化或顺应新知识的过程；又是一种结果，即对新知识的把握和领悟．理解包括对于一个对象“是什么”和“为什么”两个层面，前者是基本层面，后者是深化层面．基本层面指对知识意义的理解，能从不同角度去认识知识的性质、知识的类属以及知识的背景；深化层面是对知识之间逻辑关系的理解，即理解知识与其它知识的联系、知识之间的因果关系．

知识理解的第二层涵义，是指基本技能的形成和发展．一方面，知识的理解不能脱离知识的应用，应用是理解的必要环节．从知识的认知到知识的应用再到知识的认知，只有通过不断循环的过程，才能达到对知识的真正理解．知识应用的本质，是解释与知识相关的现象，解决与知识相关的问题，个体的学科基本技能就是在知识应用过程中生成和发展的．另一方面，无论是陈述性知识还是程序性知识，知识本身就蕴涵了方法．作为陈述性知识呈现的数学概念，具有“过程”与“对象”二重性．所谓过程，就是具备了可操作性的法则、原理和程序，而对象是指概念的结构和结果[9]．显然，“过程”蕴涵了方法．对于程序性知识来说，它本身就是一种操作程序的规定，这种操作程序由若干条产生式叠加而成，本质就是方法．技能是指掌握和应用专门技术的能力，数学技能就是掌握和应用数学知识的基本能力．应用与方法密不可分，因而，知识理解的本意涵盖了基本技能的形成和发展．

将知识理解作为学习者学科核心素养的一级水平，具体表现为：

（1）了解知识产生的缘由．知道知识从何而来，明白知识产生的理由；有基本的演绎和归纳推理能力；有对知识产生和发展的经历，形成了一定的活动经验．

（2）理解知识形成的结果．能够把握数学知识的过程与对象二重性，掌握基本的事实和结论；明确概念的内涵、外延，形成概念体系；理解规则与法则的结构、使用的条件，形成命题体系；掌握蕴涵在知识中的数学基本方法．

（3）解决数学的基本问题．能够辨析概念，在知觉水平和思维水平上应用知识；能使用简单知识、基本规则和基本方法解决简单的数学问题．

3.2 知识迁移

知识迁移是指学习者把理解的知识、形成的基本技能迁移到不同的情境中去，促进新知识的学习或解决不同情境中的问题．

第一，知识迁移是知识在新情境中的应用．所谓新情境是指不同于学习这个知识时的情境，因此，知识迁移不是知识的简单应用，不是知识的模仿应用．能否辨认当前情境中问题的类属而对原有知识进行准确的激活？能否判断知识迁移的有效性？当发现所选的知识或方法不能解决当前问题时能否灵活转向激活其它知识？这些因素本身就反映了学习者的能力，是个人数学核心素养的一种体现．

第二，知识迁移是知识的综合应用．解决一个数学问题时，用到的知识或方法可能不是单一的，往往涉及多个知识或多种方法，这就需要学习者有丰富的知识资源，并能选择有用的资源在新的情境中进行组合．因此，知识迁移是多个知识或多种方法向一个目标的迁移，是多个旧情境中的知识向同一个新情境迁移的过程．知识迁移要求学习者具有识别、判断、筛选、决策等多种能力．

将知识迁移作为学习者学科核心素养的二级水平，具体表现为：

（1）有基本的类比推理能力，能够将知识迁移到不同情境中去，解决与数学知识相关的现实情境问题、数学内部不同情境问题、不同学科情境问题．

（2）能够理解知识之间的逻辑关系，掌握知识结构，掌握与知识相关的数学思想方法，能够判断知识迁移的准确性和有效性．

（3）能够解决需要多种知识介入、多种方法运用的常规性复杂问题．

3.3 知识创新

知识创新的一层涵义是指学习者能够解决一些非常规的开放性问题；或者生成超越教材规定内容的数学知识；或者对问题进行推广与变式得到一个新的问题．知识创新的另一层涵义是指学生能够用数学思维去看待和处理一些现实生活中的问题．“创新”是相对学习者而言的，对于他们来说是新知识、新方法．以自我的“发现”得到的知识，就是知识创新．

首先，知识创新是学习者对教学内容的拓展与延伸．知识之间会存在依存关系或逻辑关系，新知识的产生总是与某些旧知识有内在的联系．因此，一个知识总会有自身生长与发展的空间．对于学生而言去探究知识的拓展过程和获得的结果都是知识的创新．其次，知识创新是学习者对问题的推广与变式．创新元素往往隐藏在问题解决之后，因为问题被解决并不意味着对问题探究的结束．许多数学问题都有可能通过变式、改变条件、类比推理等手段而产生出新的问题，当把变式推广的问题解决之后，就能得到一个新的知识．此外，知识创新的另一种显示是学习者在解决问题过程中实现了方法的突破，能够解决一些非常规的开放性问题，在解决问题中突破常规的方法就是知识创新．

更重要的是，知识创新表明学习者形成了学科思维．学科思维“表现为学科特有的理解问题和分析问题的思维方式，这是学习者能够像学科专家一样深入思考问题时所需要的一种能力”[12]．学习者形成学科思维，表明他们能够领悟学科思想方法，体会学科价值观，有批判和反思的意识，并用学科思维方式看待和处理学科及非学科的问题．形成学科思维应当是学习者学科核心素养发展的最高表现．

将知识创新作为学习者学科核心素养的三级水平，具体表现为：

（1）具有探究问题的意识．在学习中养成反思的习惯，有爱思考、善于提出数学问题的学习行为．

（2）具备探究问题的能力．有较高的直觉能力、合情推理能力，具有批判性思维能力和反思能力，能够提出富有见解的数学猜想，具备对问题的证伪和证实的能力，能够对数学问题进行变式、拓展和推广．

（3）具备解决非常规数学问题的能力．能够灵活运用知识和方法解决非常规性问题．

（4）形成数学思维．能够用数学思维对事物进行判断和分析，初步形成数学学科特定的认识世界和改造世界的世界观和方法论．

4 数学核心素养评价的框架

4.1 一个评价框架

上面讨论了数学核心素养的生成源于知识，而知识理解、知识迁移和知识创新既反映了学习的3种水平，又蕴涵由学习转化而来的数学核心素养形成的3种水平，这样，就为学生学科核心素养的评价提供了一个理论框架（见表1）．

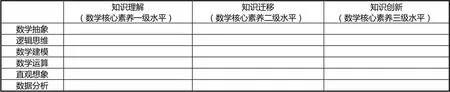
表1 学科核心素养评价框架

与PISA（2012）的框架对比．PISA模型中是7种数学基本能力：交流，数学化，表述，推理和论证，设计问题解决策略，运用符号的、正式的、技术的语言和运算，使用数学工具，而表1依据的是中国目前提出的6种数学核心素养．PISA模型中的过程维度：表述、运用、评估，是解决问题过程中某种能力的表现形式，可以视为一种水平划分，但是这种划分是针对解决问题来说的，不能涵盖在学习过程中对数学核心素养的评价．而表1给出的框架，可以用于在学习过程中对核心素养形成的评价，也可用于综合测试中对核心素养水平的评价，当然，在平时学习中，对数学核心素养的评价必须与学生学习的具体内容结合，在综合测评中，考察的是知识的综合应用．

表1的框架与布卢姆关于认知领域的评价是相通的，都是通过知识的学习来对能力进行评价，不同的是布卢姆模型的水平划分过细，水平之间的边界不是十分清晰，并且布卢姆模型没有明确指出高水平阶段就是评价学生的能力水平．表1的框架分为3个水平，边界比较清楚，能较好地反映各种数学核心素养的发展特质．

李艺等提出了一个3层架构，第一层是“双基”，以基础知识和基本技能为核心；第二层是“问题解决”，以解决问题过程中所获得的基本方法为核心；第三层是“学科思维”，指在系统的学科学习中通过体验、认识及内化等过程逐步形成的相对稳定的思考问题、解决问题的思维方法和价值观，实质上是初步得到学科特定的认识世界和改造世界的世界观和方法论[13]．研究者提出的核心素养3个水平与李艺提出的3层架构总体观点是一致的．

4.2 两个案例分析

下面以“集合”内容（《普通高中数学课程标准》的内容）给出具体操作说明．

并不是每一个知识的学习都能全部体现6种数学核心素养，例如表2中，“集合”内容在数学建模和数据分析方面是很难体现的．一般说来，数学抽象、逻辑思维、数学运算、直观想象的共性大，而数学建模、数据分析共性较小．

下面选取一个与PISA相关的测试题目，利用表1的框架进行分析．

试题：农场与牛．

农夫在一片长满草的大草原农场中央建了一间边长为5米的牛棚（假设牛棚部分没有草），农夫在一个墙角拴了一头牛，如果绳子长12米，若绳子可自由弯曲，请问牛共可吃多少面积的草？

问题（1）：请问下列哪一个图是正确的？

(A)         (B)

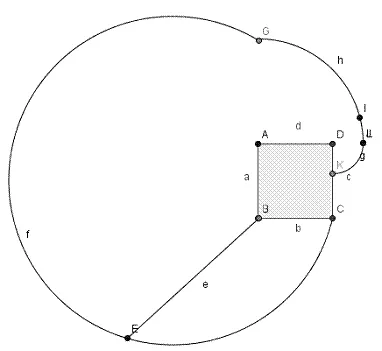
(C)          (D)

问题（2）：请问牛吃了多少面积的草地？

（A）约452平方米；（B）约427平方米；

（C）约416平方米；（D）少于413平方米

（选自林福来主编台湾2011数学素养评量样本试题）

应当说，这是一个考察数学素养比较好的题目，要用数学知识并根据学生的生活经验去解决现实生活中的问题．但是，考察知识的创新方面显得不足．下面对此题以知识理解、知识迁移、知识创新为目标进行改造，并分析所考察的数学核心素养水平．

首先，该题的知识理解部分比较简单，只需学生掌握圆面积公式，会运用这个公式解决问题．题目中的问题1和问题2属于同一个层面，即知识的迁移，增加一个问题3，可以考察学生的知识创新．

问题3：在解决了这个问题之后，你能否把得到的结论作一般化处理；或者由这个问题提出一些新的问题，并解决你提出的一个问题．

要对问题作一般化处理，需要把具体数字用字母替代，得到解决这个问题的一般化结论．要提出新的问题，可以从牛棚形状的变化来考虑，譬如改为长方形、菱形、圆等；可以从绳长的变化来考虑；从草地上可能存在障碍物来考虑，等等．

经过改造，由于所需要的知识很简单，因此知识理解水平可以忽略，主要考察知识迁移和知识创新两种水平．测查的数学核心素养主要包括：数学抽象——把一个现实问题抽象为一个数学问题；把问题推广引申．数学运算——将圆面积公式用于解决现实问题；公式的灵活运用．直观想象——通过观察图形，结合生活经验抽象出问题的数量关系；能够进行图形变式．

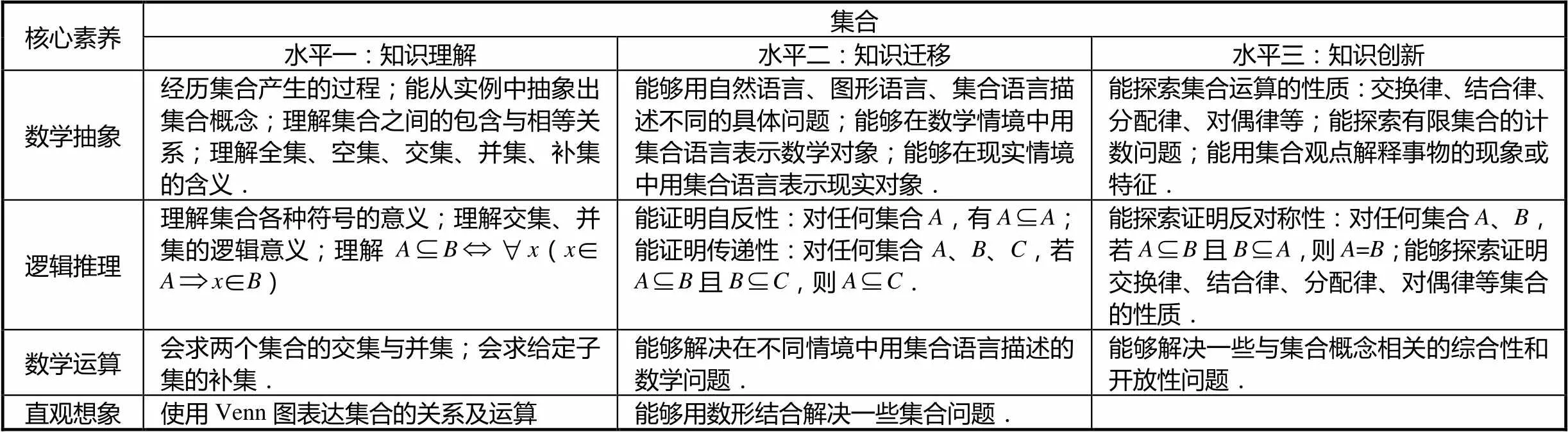
表2 “集合”内容对核心素养的评价

[1] 郑毓信．数学教育视角下的“核心素养”[J]．数学教育学报，2016，25（3）：1．

[2] 施良方．学习论学习心理学的理论与原理[M]．北京：人民教育出版社，1992．

[3] OECD2004. Learning for Tomorrow’s World First Results from PISA2003 [EB/OL]. http://www.pisa.oecd.org.

[4] 綦春霞，周慧．基于PISA2012数学素养测试分析框架的例题分析与思考[J]．教育科学研究，2015，（10）：46．

[5] Biggs J B, Collis K F.[M]. New York: Academic Press, 1982.

[6] 李佳，高凌飚，曹琦明．SOLO水平层次与PISA的评估等级水平比较研究[J]．课程·教材·教法，2011，（4）：91．

[7] 桂德怀，徐斌艳．数学素养内涵之探析[J]．数学教育学报，2008，17（5）：22．

[8] 潘小明．关于数学素养及其培养的若干认识[J]．数学教育学报，2009，18（5）：23．

[9] 斯宾塞．教育论[M]．胡毅译．北京：人民教育出版社，1962．

[10] 瞿葆奎，施良方．“形式教育”论与“实质教育”论[M]．华东师范大学学报，1988，（1）：9；（2）：27．

[11] 加涅．学习的条件和教学论[M]．皮连生，王映学译．上海：华东师范大学出版社，1999．

[12]  Sfard A. On the Dual Nature of Mathematical Conception, Reflections on Processes and Objects as Different Sides of the Same Coin [J]., 1991, (26): 50.

[13] 李艺，钟柏昌．谈“核心素养”[J]．教育研究，2015，（9）：46．

[责任编校：周学智]

Framework of Evaluation about Mathematics Key Competencies

YU Ping

(Institute of Curriculum and Teaching, Nanjing Normal University, Jiangsu Nanjing 210097, China)

Students’ mathematics key competencies generated, stems from a knowledge of mathematics learning. Mathematics learning performance for three forms: knowledge understanding, knowledge transfer, knowledge innovation. Three forms of knowledge to generate different levels of mathematics key competencies, Therefore, to form the evaluation of mathematics key competencies should be based on the three forms of knowledge learning. On the basis of the mathematics key competencies was divided into three different levels, This kind of level absorb the merits of the Bloom model and model of PISA, and reflect the characteristics of mathematics learning, had a dual characteristic theory and operability.

mathematics key competencies; levels of key competencies; knowledge understanding; knowledge transfer; knowledge innovation

G40–03

A

1004–9894（2017）02–0019–05

2016–12–04

江苏省社科基金项目——中小学生数学核心素养体系建构与教学实践研究（15JYD001）；江苏省教育厅重大项目——义务教育学科核心素养和关键能力研究（2015JYKTZD-02）

喻平（1956—），男，重庆人，教授，博士，博士生导师，主要从事数学课程与教学论研究．