小学数学教科书中的比及其教学
2017-05-06史宁中娜仁格日乐
史宁中,娜仁格日乐
小学数学教科书中的比及其教学
史宁中,娜仁格日乐
(东北师范大学数学与统计学院,吉林长春 130024)
在现行小学数学教科书,都把两个数的比定义为两个数相除,这样的定义不仅削弱了比的现实功能,而且无法让学生感悟比的数学本质.论证了比的本质是两个数量倍数关系的表达与度量,还论证了比与除法、分数、比例的差异.并且,对相关内容的教学提出了建议.
比;倍数关系;表达;度量;除法;分数;比例
在小学数学教学中,比是非常重要的概念,是教学的重点和难点.中国现行小学数学教科书,都把这些内容安排在六年级上册,并且都把比定义为除法的一种表达形式、通常表示为分数的形式,参见表1.

表1 小学数学教科书的比的定义
像教科书这样的表述,必然会引导人们把比理解为一种运算、是除法运算的一种特殊形式,进而理解比是为了得到运算结果.这样的理解不仅大大削弱了比的现实功能,并且很难、甚至无法让学生感悟比的数学本质.那么,应当如何理解比、进而理解比的教学价值呢?应当实施一种什么样的数学教学呢?
1 在日常生活中人们如何使用比的概念
小学数学教学似乎应当秉承这样一个基本理念:概念的引入要源于生活、至少应当与日常生活的经验不悖.为此,先分析一下,人们在日常生活中如何使用比的概念.
两个数量的表达.在球类比赛中,通常要使用比这个词,比如,甲乙两个足球队某场比赛结果是三比二、记为“3:2”,这时的比是两个球队进球数量多少关系的表达,如果按照教科书的定义,把比赛结果“3:2”说成运算结果“1.5”是不符合常理的;特别是,在足球比赛中,往往会出现进球数为0的情况,对于这种情况,把比赛结果“2:0”理解为除法就更无法解释了.为了自圆其说,教师在教学过程中只能说:这样的比与数学所说比的意义不同,甚至特别强调说:不能把生活经验与数学概念混淆.于是,就是这样,教科书迫使数学从小学阶段就脱离了生活.事实上,应当反过来思考这样的问题:能不能给出一个包含生活用语在内的比的数学概念呢?
含量多少的表达.在超市中,几乎所有饮料都标明成分构成,或者用“3:1”的形式标明饮料中果汁的比、或者用“75%”的形式标明果汁浓度.无论采用那种形式,这时的比都是饮料中果汁含量多少关系的表达.在日常生活中,这种表达形式的比最为常见,不胜枚举;并且在大多数情况下,这样的表达并不需要像除法运算那样得到运算结果.因此,严格套用教科书的定义,这种形式的比也不是数学中的比.但是,无论如何,不能把这种在日常生活中广泛使用的比的形式排除在数学之外.
综上所述,研究者需要做的事情是重新构建比的概念,而不是千方百计地解释现有概念.为此,需要重新审视现有概念,问题的核心是,比与除法运算的关系到底是什么、是如何表现的?
构建一种度量.教科书中有这样的例子[1]:
“神舟”五号进入运行轨道后,在距地350 km的高空做圆周运动,平均90分钟绕地球一周,大约运行42 252 km.我们也可以用比来表示路程和时间的关系:路程和时间的比是42 252比90.记作42 252:90.
这是一个很好的例子.事实上,只有在这样的例子中比才涉及到除法,因为这时的比需要得到除法运算的结果.因此按照惯例,教科书应当进一步引导学生理解:表示路程和时间关系的比为速度:路程/时间=速度,因此“神舟”五号的速度为:42 252(千米)/90(分)≈469.47千米/分,而不是像教科书那样仅仅给出比的形式,而不论及计算结果.
2 如何表述比的概念
通过上一节基于生活现实的讨论,可以这样给出比的概念:
比是两个数量倍数关系的表达或者度量. (1)
如果认为这样的表述过于学术化,那么,在小学数学的教科书中可以使用更加通俗的语言,文章第四节将会比较详细地讨论这个问题.
无论如何,在上面的表述中,需要很好地理解什么是“倍数关系”.《现代汉语词典》中关于比的定义很好,但不够全面[5]:
比较两个同类数量之间的倍数关系,叫做它们的比,其中一数是另一数的几倍或几分之几.
因此,倍数关系是指比较量多少的一种关系;并且,把倍数单纯理解为整数是不可以的,这样的理解给小学数学教学带来许多不必要麻烦[6].研究者现在认定,在定义(1)中,所说的倍数既包括整数也包括分数1.关于比,在《数学辞海》中也有类似的表述,但没有解释“倍数关系”的含义[7]:
比(ratio)亦称单比.算数术语.比较两个同类量之间的一种倍数关系,称为这两个同类量的比,在单位相同时,两个量的比可以用表示这两个量的数的比来代替.在实际中,只有同类量,且取同单位,才能相比,两个量相比得到的倍数,称为比值.两个数相比可以说成是两个数相除.
但是,作为数学的定义,无论是《现代汉语词典》还是《数学辞海》的表述都不够全面,主要有两方面的问题:一是只局限于同类数量,二是都没有涉及度量.显然,这样的定义不能包括上一节中“构建一种度量”的情况.
定义(1)的表述包含了上一节论述的所有情况,“两个数量的表达”和“含量多少的表达”对应的是:两个数量倍数关系的表达;“构建一种度量”对应的是:两个数量倍数关系的度量.
关于“两个数量倍数关系的表达”相对容易理解,虽然所有小学数学教科书都没论及这种情况,研究者在下一节对比概念的历史回顾中进一步讨论这个问题.在此特别强调的是,比的度量功能是重要的,在许多情况下,借助比的度量可以构建非常有意义的新概念,因此,比的度量功能逐渐成为现代数学应用的核心.并且,对于比的度量功能,在大部分情况下两个数量不是同类的量.除了上一节谈到的速度之外,再分析几个例子.
夏普比.所有投资活动都涉及两个相互关联的基本要素:收益和风险.人们总是希望选取收益大、风险小的投资策略,但事实上往往二者不可得兼:收益越大则风险越大.那么,应当如何度量投资策略的好坏呢?
1964年,美国经济学家夏普提出一种度量方法,本质上就是考虑收益与风险之比:收益/风险,人们称这个比值为夏普比(Sharpe ratio).可以把这个比值直观理解为:单位风险的收益,因此比值越大投资策略越好.现在,夏普比已经成为经济学中综合考虑收益与风险的三大经典指标之一,主要因为这个工作,夏普获得1990年度诺贝尔经济学奖[8].
信噪比.在现代社会,信号的传送与接收变得越来越重要.影响信号接收主要有两个相互关联的基本要素:灵敏度与噪声.人们总是希望接收系统灵敏度高且噪声小,但事实上往往二者不可得兼:灵敏度越强则噪声越大.于是与夏普比的情况类似,人们用灵敏度与噪声之比度量接收系统的有效性,称之为信噪比(signal-to-noise ratio),可以把这个比值直观理解为:单位噪声的信号强度,因此比值越大接收系统越好[9].现在,信噪比已经成为表征系统有效性与抗干扰性的主要质量指标之一,广泛应用于产品质量控制和国防信号系统.
优度比.这是数理统计学的一个重要概念[10].比如,希望比较和两种药物的有效性.假如服用A和B两种药物的病人数分别是和,一段时间后痊愈病人数分别是和.显然,仅仅通过痊愈人数比较药物有效性是不合理的,还需要考虑没有痊愈的人数,人们用比值和分别刻画两种药物的有效性,称之为优度.为了计算概率方便,通常用比值
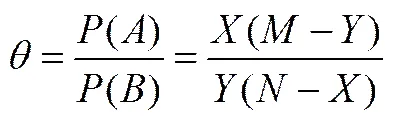
考查药物的有效性,称为优度比(odds ratio),比值越大说明药物比药物越有效.这种方法几乎适用于所有产品好坏的度量.
总结上面3个例子可以看到,如果要对一个事物的优劣进行度量,可以探寻影响优劣的关键要素,然后基于关键要素之比构建度量指标.基于这个思路,可以根据生活的经验创设教学活动,让学生在这样的活动中感悟:数学是如何利用两个数量的比合理地分析和解决问题的.并且让学生逐渐建立这样的理念:可以人为地建立各种度量指标,判断度量指标好坏的标准就是更好反映客观现实.比如,在比的度量功能的教学中,可以考虑下面的例子.
同学胖瘦比较.通常人们会认为,一个人的体重决定这个人的胖瘦,但在大多数情况下,还应当考虑这个人的身高.那么,如何基于体重和身高这两个要素构建度量指标呢?在教学活动中,教师可以启发学生自由想象,比如,可以把身高分成几个区间然后考查体重,也可以把体重分成几个区间然后考查身高.在这样的过程中,在教师的引导下,学生会逐渐发现,所谓“胖”与体重成正比、与身高成反比,因此,可以用体重与身高之比作为度量指标2.
班级学业比较.在通常情况下,人们用两个班级的平均分比较两个班级学业的好坏.但在事实上,一个班级学业质量的好坏是指这个班级大多数学生学业质量的好坏:不仅平均分要比较高、并且全班学生成绩差异不大.因为成绩的方差(标准差)可以度量学生成绩的离散程度,因此,可以基于平均分和标准差这两个要素构建度量指标:“平均分/标准差”.之所以用标准差而不用方差,是因为在这个问题中,比的前项与后项是同类的量,单位一致才能反映客观现实.
3 比概念的历史回顾与表达的重要性
在上一节,通过一些实例讨论了比的度量功能、以及这个功能的教育价值.事实上,回溯数学的发展史,比作为一种数学表达是极为重要的,这恰恰是小学数学教科书所忽略的,这是因为“两个数的比表示两个数的相除”这个命题的限制:作为运算的除法不具有表达功能.
比作为一种数学的表达.作为一种数学的表达,比这个概念广泛应用于物理学基本概念和基本结论的表述.认真阅读牛顿的巨著《自然哲学之数学原理》就会发现,几乎对于所有的结论,牛顿都是用比的概念予以表达[11].作为说明,研究者分析两个最为重要结论的表述:一个是关于力,一个是关于万有引力.
关于力,牛顿在巨著的定义2和定律Ⅱ中说:
定义2. 运动的量是运动的度量,可由速度和物质的量共同求出.
定律Ⅱ. 运动的变化正比于外力,变化的方向沿外力作用的直线方向.
关于万有引力,牛顿在巨著的第一编第12章命题76的两个推论中说:
推论Ⅲ. 一个球对于另一个球的运动吸引,或二者间的相对重量,在相同的球心距离处,共同正比于吸引的与被吸引的球,即正比于这两个球的乘积.
推论Ⅳ. 在不同的距离处,正比于该乘积,反比于二球心距离的平方.
牛顿的这种表述方法源于古希腊学者对比的认识,古希腊学者最初用比的概念表述几何现象,而运动的表述与几何的表述是密不可分的.据说,牛顿最初对数学并没有兴趣,是他读了欧几里得的著作《原理》之后才热衷于数学,开始了他天才的思考[12].正因为如此,牛顿巨著《自然哲学之数学原理》的体例完全模仿欧几里得的著作《原理》.
线段长度大小关系的表达.欧几里得《原理》第五卷3,开篇给出了18个关于量、比和比例的定义.下面,介绍前6个定义[13]:
(1)当一个较小量能尽一个较大量时,把较小量叫做较大量的部分.
(2)当一个较大量能被较小量尽时,把较大量叫做较小量的倍量.
(3)两个同类量之间的大小关系叫做比.
(4)当一个量几倍以后能大于另一个量,则说两个量有一个比.
(5)有4个量,第一量比第二量与第三量比第四量叫做有相同比,如果对第一与第三量取任何同倍数,又对第二和第四量取任何同倍数,而第一与第二倍量之间依次有大于、等于或小于的关系,便有第三与第四倍量之间相应的关系.
(6)有相同比的4个量叫做成比例的量.
虽然上面定义中,欧几里得所说的是“量”,但从第五卷后面的内容看,这里所说的“量”指的是线段长度,因此希尔伯特在《几何基础》中,在进行了一些线段性质的证明之后说[14]:“线段的量的比较即线段的长短的比较”,并且特别在这几个字的下面赋予加重符号.
分析上面6个定义,欧几里得似乎把问题说得过于繁杂,并且把比定义为线段长度大小关系的表达,因此考虑了大于、等于和小于3种关系.从现在的角度看,如此繁杂述说主要是因为两方面原因:一是那个时代还没有创造出更多的数学符号用以表达;二是那个时代对无理数还没有清晰的认识.欧几里得认为,如果线段和是两个可以公度的量,那么比:(或者/)就对应于数(有理数),如果这两个线段不可以公度,那么就用大于或小于号表示,这样就处理了无理数的问题.据说,这种思想来源于古希腊学者欧多克斯,孕育了戴德金用有理数的分割定义实数这种思想的萌芽[15].
借用现代数学语言,从纯数学的角度,可以把上面的6个定义简约表述为:
比:称两个量和的倍数关系为这两个量的比,表示为:.
三歧性:与数一样,两个比之间存在3种关系:大于、等于、小于,当且仅当其中一种关系成立.
比例:称、与、之间具有比例关系,如果:=:,则对任意非零数和都有:=:. (2)
其中,量,,,可以用来表示线段(长度);符号“:”是比的符号,据说是莱布尼茨最初使用了这个符号,既表示比也表示除法[16].
基于上述最后一个命题,希尔伯特在《几何原理》中用整整一章的篇幅讨论了线段比例的性质,并称之为欧几里得比例论[14].
比与古代人们的现实生活.欧几里得用比的概念研究线段长度的关系,绝对不是空穴来风,是有深厚生活背景的.现举两个例子说明这个问题,一个是关于音乐的,一个是关于美学的.
比与音乐.古希腊学者毕达哥拉斯发现,可以把音乐归结为线段长度之间的关系:两个绷得一样紧的弦,如果一根是另一根长度的二倍,就会产生和谐的声音,两个音相差八度;如果两个弦长的比为3:2,就会产生另一种和谐的声音,两个音相差五度.由此可以得到一般结论:音乐的和声在于多根弦的长度成整数比,比如,3根弦的弦长比为3:4:6.这样就发明了音阶,一本书中生动地描述了毕达哥拉斯发现和声规律的故事[17].
几乎在相同的时期或者更早一些,在古代中国,一个类似的定音阶的方法被称为“三分损益法”,记载在《管子》这部书中4,命名得到的五声音阶分别为:宫、商、角、徵、羽.
比与美学.有经验的主持人一般不会站在舞台的边角或正中央,而是站在舞台宽度的黄金分割点上,这时声音会更加悦耳,视觉上也会产生美感[18].黄金分割也是源于欧几里得的《原理》,第Ⅵ卷开篇定义[13]:
3. 分一线段为二线段,当整体线段比大线段等于大线段比小线段时,则称此线段被分为中外比.
根据欧几里得的定义,如果把整体线段(长度)作为1、大线段(长度)作为、小线段(长度)作为,那么,黄金分割点(中外比)是指的长度满足比例关系
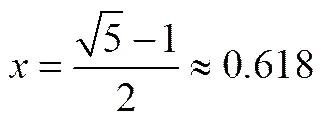
这就是黄金分割点.黄金分割点是一个无理数,已经超出了可公度(有理数)的范畴.黄金分割点有一个很特殊的几何性质:建立一个黄金分割矩形,即矩形的长为1、宽为,如果在矩形中截取一个边长为的正方形,剩余的矩形仍然为黄金分割矩形,并且在理论上,这样的方法可以无限制地进行下去.人们把这样的思想用于实验设计,比如20世纪六七十年代,华罗庚在全国范围内所推广的优选法就是基于黄金分割.
从古希腊开始,人们认为黄金分割体现了和谐的美,因此把黄金分割广泛应用于绘画、雕塑和建筑.现代生活中,银行卡、名片等的矩形中,长与宽的比通常采用的是黄金分割,认为这样的矩形美观大方.
4 比概念的小学数学教学
通过上面的讨论,可以清晰地界定比的数学本质:表达和度量两个数量的倍数关系,就像(1)所表述的那样.但是,这样的界定过于学术化.那么,在小学数学教科书中、进而在小学数学教学中应当如何引入比的概念呢?或者更确切地说,应当如何定义比的概念呢?
创设情境让学生感悟.一般来说,数学定义有两种形式[19]:一种是基于对应的名义定义,一种是基于内涵的实质定义.
名义定义是对某一类事物标明符号或指明称谓.标明符号就是用符号表达所要研究的对象,比如(2)那样的表达;指明称谓就是通过举例,给研究对象起个名字,比如,称这样的图形为线段.指明称谓的名义定义方法比较适合小学数学教学,学生可以比较形象地接受概念.因此,创设揭示内涵的情境、举出恰到好处的例子是非常重要的,因为这样的定义不是通过语言表述研究对象内涵,而是通过例子让学生感悟研究对象内涵.
基于上述比的本质,如果用指明称谓的方法引入比的概念,那么,设计的情境要针对数量的倍数关系,举出的例子要把握表达或者度量.
对于表达,大部分教科书采用国旗长宽比的例子,或者饮料果汁比的例子是切实可行的,但最后应当有这样的结论:这样的比表示了国旗长度与宽度,或者饮料中果汁与非果汁的多少关系(倍数关系).基于表达的进一步拓展,需要注意两件事情:一是可以过度到比例,就像(2)表述的那样;二是可以过渡到正比、反比,就像第二节中物理学的例子.最终,这样的表达可以发展为正比例关系和反比例关系.
对于度量,有两种情况需要考虑,一种是同类量的倍数关系,一种是非同类量的倍数关系.对于前一种情况,可以用名片说明(3)的关系,然后把0.618带入(3)中验证黄金分割解的正确性,得到比值:宽度/长度≈0.618,感悟作为度量的比,感悟比与现实生活的关联;对于后一种情况,可以用第一节或第二节中的例子,比如:速度=距离/时间,让学生通过比值的单位:千米/分,感悟作为度量的比,感悟比在自然科学中的应用.
综上所述,小学数学关于比的教学,最好要有情境、举例说明,情境可以是生活的、也可以是数学的或者科学的;举出的例子要明确针对的是表达的比、还是度量的比.另一方面,教师一定要知道学生认识和理解比的思维过程,有的放矢地开展教学活动.
与除法、分数的差异.除法是一种运算,是一种在解决问题的过程中使用的计算方法.因此,比的表达功能与除法风马牛不相及,比如,用“3:1”的形式标明饮料中果汁与水的比,如果把这样的比理解为除法运算就完全背离了表达的本意.对于比的度量功能,有两种情况:一种情况与除法运算没有直接关系,比如,通过(3)式求黄金分割点;一种情况要用到除法运算,比如,速度=路程/时间.即便是后一种情况,比也是通过除法运算得到速度的度量、而不是除法运算本身.所以,不能把比理解为除法.
虽然可以用分数的形式表示比,但在本质上:分数是一个数、并且是一个无量纲的数;而比是一种表达或者度量,是可以有量纲的.因此,用分数形式表示的是比的大小、而不是比本身.所以,也不能把比理解为分数.特别是,研究者在前面已经反复提到,在一般意义上比可以是无理数.
与比例的关系.虽然在(2)的第三个式子中,也用两个比相等的式子来表示比例,但后面的充分必要条件则更为本质,这个条件蕴含了两个变量倍数关系的不变性.小学阶段的数学设定比例、正比例、反比例的内容有两个目的:一是为了日常生活的需要,二是为了初中、高中阶段学习函数做铺垫.因此,这些内容的教学应当让学生感悟变量、以及变量之间的关系.在这个意义上,比是变化中的静止、是函数关系的具体取值.
[1] 户江,杨刚.义务教育教科书数学六年级(上册)[M].北京:人民教育出版社,2014.
[2] 孙丽谷,王林.义务教育教科书数学六年级(上册)[M].南京:江苏教育出版社,2014.
[3] 刘坚,孔启平,张丹.义务教育教科书数学六年级(上册)[M].北京:北京师范大学出版社,2014.
[4] 张天孝.义务教育小学实验教科书数学六年级(上册)[M].杭州:浙江教育出版社,2010.
[5] 中国社会科学院语言研究所词典编辑室.现代汉语词典[M].北京:商务印书馆,2002.
[6] 史宁中.基本概念与运算法则:小学数学教学中的核心问题[M].北京:高等教育出版社,2013.
[7] 数学辞海编委会.数学辞海(第1卷)[M].太原:山西教育出版社,2002.
[8] 史树中.诺贝尔经济学奖与数学[M].北京:清华大学出版社,2002.
[9] 鞠德航,林可祥,陈捷.信号检测理论导论[M].北京:科学出版社,1977.
[10] 史宁中.统计检验的理论与方法[M].北京:科学出版社,2008.
[11] 牛顿.自然哲学之数学原理[M].王克迪译,袁江洋校.北京:北京大学出版社,2006.
[12] 吴文俊.世界著名科学家传记·数学家Ⅲ[M].北京:科学出版社,1992.
[13] 欧几里得.几何原本[M].兰纪正,朱恩宽译.梁宗巨,张毓新,徐伯谦校.西安:陕西科学技术出版社,1990.
[14] 希尔伯特.几何基础[M].江泽涵,朱鼎勋译.北京:科学出版社,1995.
[15] 科士青.几何学基础[M].苏步青译.北京:商务印书馆,1954.
[16] Florian Cajori.[M]. Chicago Illinois: The Open Court Publishing Company, 1952.
[17] 辛格.费马大定理[M].薛密译.上海:上海译文出版社,2005.
[18] 李大潜.黄金分割漫谈[M].北京:高等教育出版社,2007.
[19] 史宁中.试论数学推理过程中的逻辑性:兼论什么是有逻辑的推理[J].数学教育学报,2016,25(4):1-16.
1 事实上,可以把“倍数”拓展到任意实数,比如说:π是圆的周长与直径之比.
2 人们又称这样的度量指标为体重指数、或BMI(Body Mass Index)指数,通常用体重(公斤)与身高(米)平方之比作为度量指标.
3 原著全书13卷,前6卷论述平面几何,第7~9卷论述数的理论,第10卷论述无理数,第11~13卷论述立体几何.后来,希普西克勒斯补第14卷,又将晚期的一些评注编为15卷,拉丁文本为《欧几里得原本》.中国最早的译本完成时间是在明万历三十六年,即1607年,是意大利传教士利玛窦和徐光启合作翻译的.他们是根据德国人克拉维乌斯1574年拉丁文的《欧几里得原本》翻译的.原书15卷,他们翻译了前6卷,因为主要是平面几何的内容,因此利玛窦和徐光启定名为《几何原本》,中文的几何的名称也就此产生.
4 相传《管子》的作者是管夷吾.管夷吾,前730—前645,又名敬仲,字仲,安徽颖上人,春秋时期齐国著名政治家,曾任齐国上卿(丞相).
[责任编校:周学智]
Ratio of Primary School Mathematics Textbooks and Its Teaching
SHI Ning-zhong, NA Ren ge ri le
(Northeast Normal University, School of Mathematics and Statistics, Jilin Changchun 130024, China)
In the current mathematics textbooks for primary schools, the ratio of two numbers was defined as the division between them. Unfortunately, this definition not only weakens its practical functions, but also caused the difficulty of grasping its mathematical essence. On the one hand, this paper argued that the essence of the ratio was the expression and measurement of multiple relations of the two numbers. On the other hand, it demonstrates the difference among division, fraction, and proportion. Finally, it puted forward some suggestions on the teaching of related contents.
ratio; multiple relations; expression; measurement; division; scores; proportion
G622
A
1004–9894(2017)02–0001–05
2017–03–02
史宁中(1950—),男,江苏南京人,教授,统计学博士生导师,数学课程与教学论博士生导师,主要从事数理统计与数学教育研究.
