低雷诺数下柔性翼型气动性能分析1)

陶真新李绍斌†,3)宋西镇

∗(北京航空航天大学能源与动力工程学院，航空发动机气动热力国家级重点实验室，北京100191)

†(先进航空发动机协同创新中心，北京100191)

低雷诺数下柔性翼型气动性能分析1)

陶真新∗,2)陶真新，硕士，主要从事柔性翼型的非定常气动力研究.E-mail：tao zhenxin@163.com李绍斌∗,†,3)宋西镇∗

∗(北京航空航天大学能源与动力工程学院，航空发动机气动热力国家级重点实验室，北京100191)

†(先进航空发动机协同创新中心，北京100191)

基于流固耦合方法对吸力面5%至95%弦长处为三段柔性结构的NACA0012翼型绕流进行了数值模拟，研究了不同弹性模量下柔性翼型的气动性能和结构响应.结果表明：在大攻角下，翼面变形影响着翼型表面的非定常流场，起到延缓失速和提高升力的作用；失速后柔性翼的升力系数下降得较为缓慢，且柔性越大，升力系数下降得越平缓；适当减小弹性模量能够提高翼型的气动性能，然而弹性模量过小反而不利于翼型气动性能的提升，并且翼面会产生大幅度的振动.

流固耦合，柔性翼型，气动性能，变形

翼型或叶型作为机翼及叶片的基础，对飞行器的气动性能起着重要的影响.当攻角大于临界攻角时，翼面气流将发生大面积分离，升力急剧下降进入失速状态，严重危及飞行器的安全.目前，常规翼型的设计及使用已趋近理论水平的极限，如何进一步拓宽翼型的稳定工作范围，提升气动性能水平是研究人员面临的一个重要的课题.

飞行生物通过升力翼面的变形能展现超高的飞行能力[1].受仿生学的启发和材料科学的发展，人们期望将柔性材料运用到飞行器的设计中，实现对流动的控制.近年来，国内外学者在这方面开展了诸多研究.微型飞行器薄膜翼的研究发现薄膜翼与流场的耦合振动能够提高升力、延缓失速[2].Wu等[3]在NACA0012翼型上表面引入弹性翼面，通过控制吸力面的上下振荡产生适当行波，抑制了主流区的分离.Curet等[4]和Gabor等[5]通过激励方式控制翼型局部变形以及郭秋亭等[6]对三段翼型的主翼段引入抛物型局部主动振动模型，翼型的升力系数也都得到了提升.康伟等[7]在翼型上表面前缘局部区域引入弹性结构，弹性部分在非定常气动力的作用下发生自激振动，大大改善了翼型升阻特性，提高稳定攻角的范围.最近Dong等[8]在NACA0012翼型吸力面引入多段柔性翼面，利用流固耦合的方法对不同柔性分段形式进行了分析，柔性薄膜的鼓起变形抑制了分离涡的尺度，相邻柔性段之间形成的稳定小涡具有“流体滚动轴承”效应，促使吸力面前半弦长流体附体.

以上研究表明柔性翼型与流场的耦合作用会诱发柔性结构体的振动变形，改善翼面气流流动状态，适当的柔性分布和材料选取有助于翼型的增升扩稳.然而不同的结构参数和气流状态会使得柔性翼面产生不同的结构响应，从而影响翼型的气动性能.本文主要用数值方法模拟具有三段柔性结构的翼型绕流，研究不同弹性模量下柔性翼型的气动性能和结构响应.

1 计算模型与数值方法

1.1 模型与网格划分

本文以NACA0012翼型为基本翼型，对柔性翼型的绕流进行数值模拟.翼型的弦长c=0.15m，其中翼型吸力面前缘0.05c至0.95c之间为三段柔性结构，柔性段长度比为2:3:4，如图1所示.其中P1,P2,P3为三段柔性翼面的中点.柔性段之间采用固支连接方式，柔性结构的厚度为0.4mm.下翼面、前缘和尾缘部分为刚性结构.

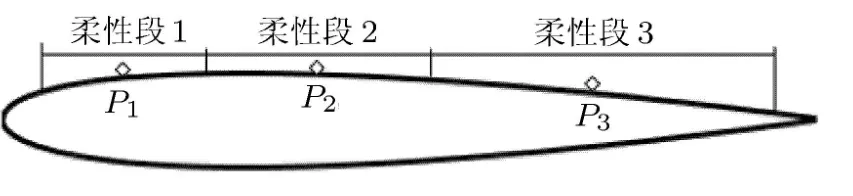
图1 柔性翼几何模型

计算域以翼型前缘为原点，进出口边界距离原点分别为10c和20c，上下边界距离原点10c.翼型近壁面采用结构化网格，考虑湍流模型的要求，翼型第一层网格厚度满足Y+≤1，沿壁面法向网格扩张因子为1.05.翼型近壁面和流场远场之间采用结构化与非结构化网格进行衔接，网格总节点数约为30000.翼型周围局部网格视图如图2所示.

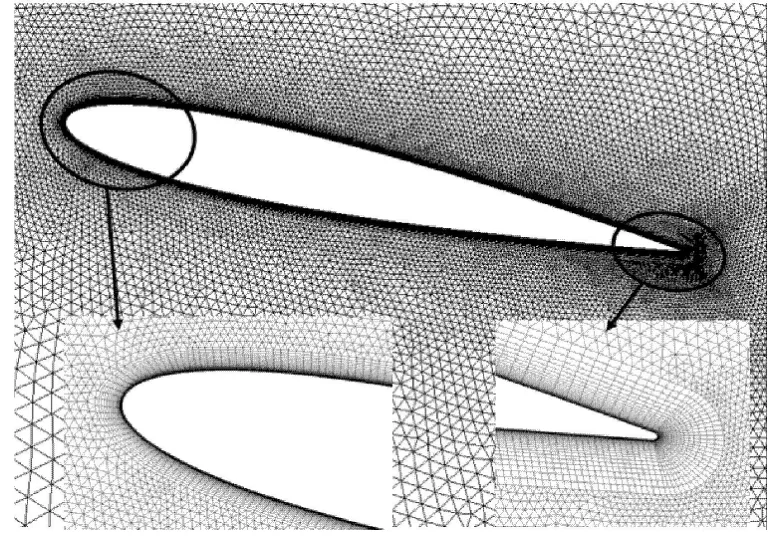
图2 局部网格视图

1.2 流固耦合数值方法

柔性结构体和流体的相互作用是典型的流固耦合问题.结构体的变形改变交界面附近流场结构，而翼面附近流场压力分布同时也影响着翼面结构的变形.在流固耦合求解过程中，流体域求解器、结构求解器和流固耦合交界面的参数传递是三个关键因素.

本文流体域采用商业软件CFX对非定常雷诺平均N--S方程进行求解，湍流模型使用k--w SST和γ--θ转捩模型.k--w SST湍流模型对层流到湍流的转捩具有比较好的捕捉能力.该转捩模型引入了新的间歇方程可表示为

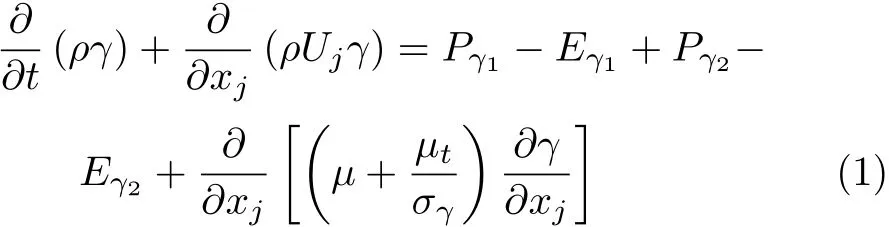
间歇因子γ表征流体处于脉动状态和非脉动状态时间比例，Pγ和Eγ为转捩项.采用High Resolution格式对方程进行空间离散，时间离散采用二阶后插欧拉格式.

使用ANSYS结构分析模块对固体域进行结构分析，柔性段采用适用于薄膜壳体的SOLSH190单元.控制方程有限元离散可写为

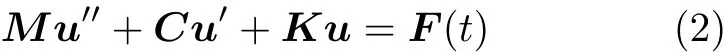
式中M,C,K分别为质量矩阵、阻尼矩阵、刚度矩阵；F(t)为流体作用在结构上的瞬态耦合力.

采用ANSYS多物理场耦合求解器MFX(multifi eld solver)实现流体求解器和固体求解器之间的数据传递.在时间推进过程中的每个时间步内，分别进行流场和结构的求解，经过交界面数据的多次迭代求解直至满足迭代收敛条件.流固耦合交界面上参数传递满足载荷守恒和能量守恒.

1.3 数值方法验证

为了对流固耦合方法进行验证，本文首先模拟了柔性薄膜翼气动激振时的翼面响应.验证模型采用Rojratsirikul等[9]的实验模型，薄膜两端被固支到安装座上，如图3(a)所示.薄膜厚度为0.2mm,弹性模量E=2.2MPa，密度ρ=1g/cm3.图3(b)给出的是自由流速度为7.5m/s,对应雷诺数Re=79700时，16◦攻角下的翼面时均变形量，并与实验值[9]进行对比.从图中可以看出，计算得到的翼面时均变形量相比于实验值略有偏小；计算得到的振动频率为43Hz，实验值为40.5Hz.计算结果与实验值吻合较好，本文使用的流固耦合数值方法可以应用于柔性翼的研究.

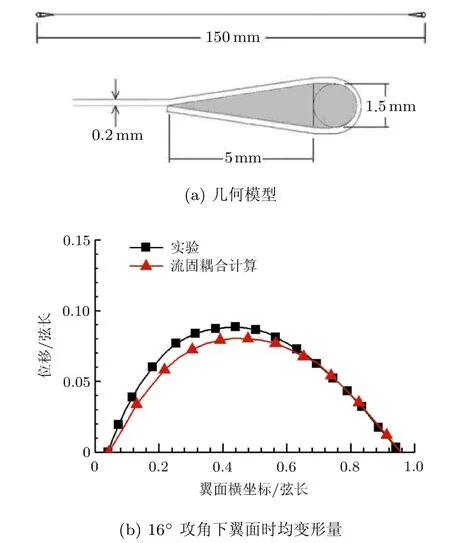
图3 流固耦合方法验证

本文主要是对翼型的气动力进行研究，因此进一步对NACA0012翼型攻角特性进行了计算与验证.计算雷诺数为135000，结果如图4所示，失速攻角相比于实验值[10]略有减小，总体上来说计算结果与实验值吻合良好，验证了数值方法对翼型气动力计算的可靠性.

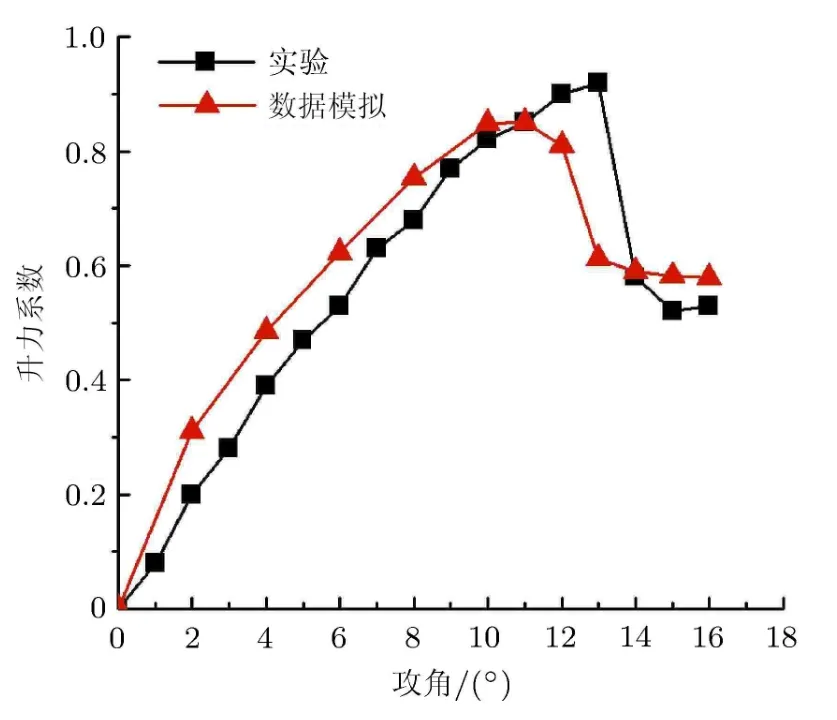
图4 刚性翼的升力系数随攻角的变化

2 结果与分析

2.1 柔性翼攻角特性

首先对两种弹性模型下的柔性翼型的攻角特性进行了计算分析.图5给出的是雷诺数为135000、弹性模量分别为2.5MPa和0.7MPa时的柔性翼升阻力系数与攻角的关系，并与刚性翼进行了对比.

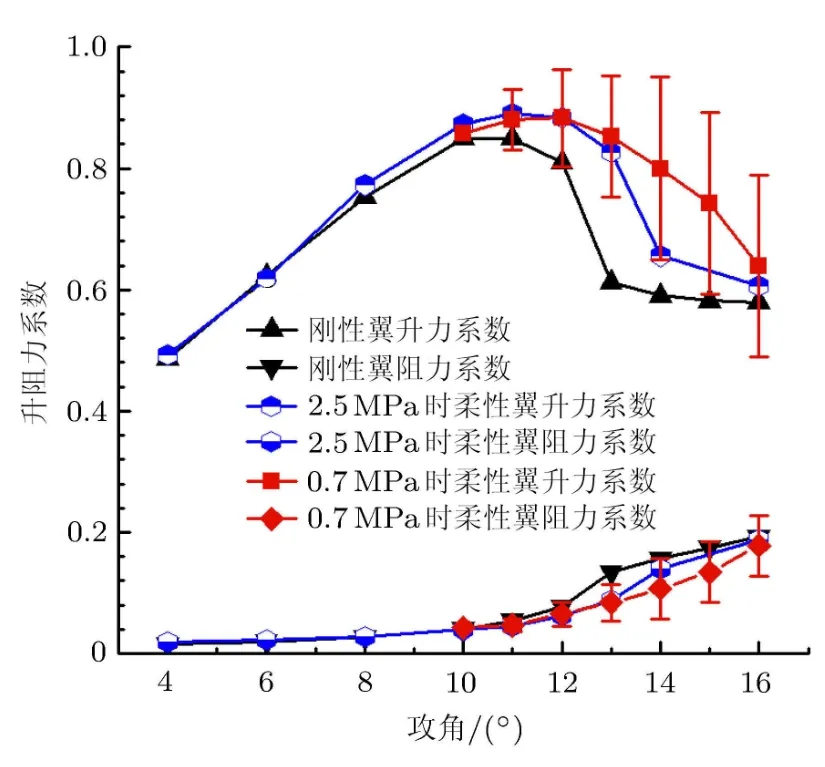
图5 柔性翼的升阻力特性

刚性翼的升力系数在8◦之前随着攻角的增大基本呈线性增加；大于8◦攻角时，时均升力系数增加的速率减慢，直至10◦攻角升力系数达到峰值，而后升力系数急剧下降.而对于弹性模量为2.5MPa时的柔性翼型，攻角在8◦之前柔性翼型的气动力系数与刚性翼的差别不大；大于8◦攻角时，随着攻角增加升力增长速率也开始减小，但相比刚性翼减小的幅度减弱；失速攻角延缓到12◦，升力峰值相比于刚性翼提升了4.7%，在特定攻角下相比于刚性翼最大提升幅度达39%(α=13◦)，同时阻力系数也得到了一定幅度的减小.而当弹性模量减小至0.7MPa时，由于此时柔性翼面发生了大幅度的振动，升阻力系数产生了大幅度的振荡，即出现了强烈的非定常现象.与弹性模量为2.5MPa相比，虽然时均升力系数峰值并没有得到提升，但在大攻角下(12◦≤α≤16◦)的时均气动力系数得到了进一步的提高，一定程度拓宽了翼型稳定攻角范围.

在较大的弹性模量下，翼型表面的流场特性还是以定常流动为主.图6给出的是弹性模量为2.5MPa时8◦,13◦和16◦攻角下柔性翼和刚性翼的时均流场结构图.在未失速攻角下(8◦)，吸力面流体附体流动，柔性翼面对翼型的气动性能影响不大.在13◦攻角下刚性翼吸力面气流已出现大范围的分离；而柔性翼的吸力面的鼓起变形能够控制翼面气流的分离，使得前缘分离流再次附体流动，从而使得升力系数大幅度提升.而对于深失速攻角下(16◦)，由于气流分离严重，翼面变形作用影响有限，并不能使得分离流再次附着，升力系数增加不明显.

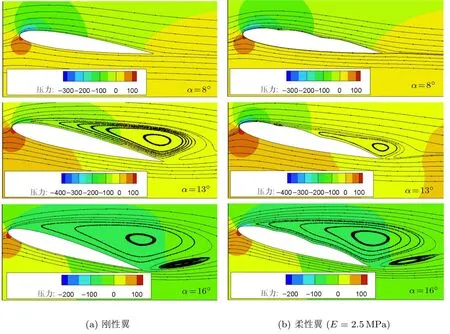
图6 不同攻角下柔性翼与刚性翼流线图

当弹性模量为0.7MPa时，柔性翼面将发生大幅度的振动，翼型表面的流场发生了强烈的非定常流动现象.图7给出的是弹性模量为0.7MPa时13◦攻角下翼型表面瞬态流场.从图中可以看出，中间柔性翼面的大幅度振动使得分离流周期性地附着在翼面上，并且会在翼面上卷起旋涡，旋涡沿着翼面向尾缘移动与脱落，导致升力系数发生了大幅度的波动.

图8给出的是不同攻角下弹性模量为2.5MPa时三段柔性翼面中点P1,P2,P3的时均变形量.前缘柔性段变形最小，后缘段柔性翼面变形量最大.在失速前，前缘两柔性段翼面的时均变形量随着攻角的增加逐渐增加，后缘柔性段时均变形量逐渐减小；失速后，前缘两柔性段翼面的时均变形量随着攻角的增加又逐渐减小，后缘柔性段时均变形量急剧增大.

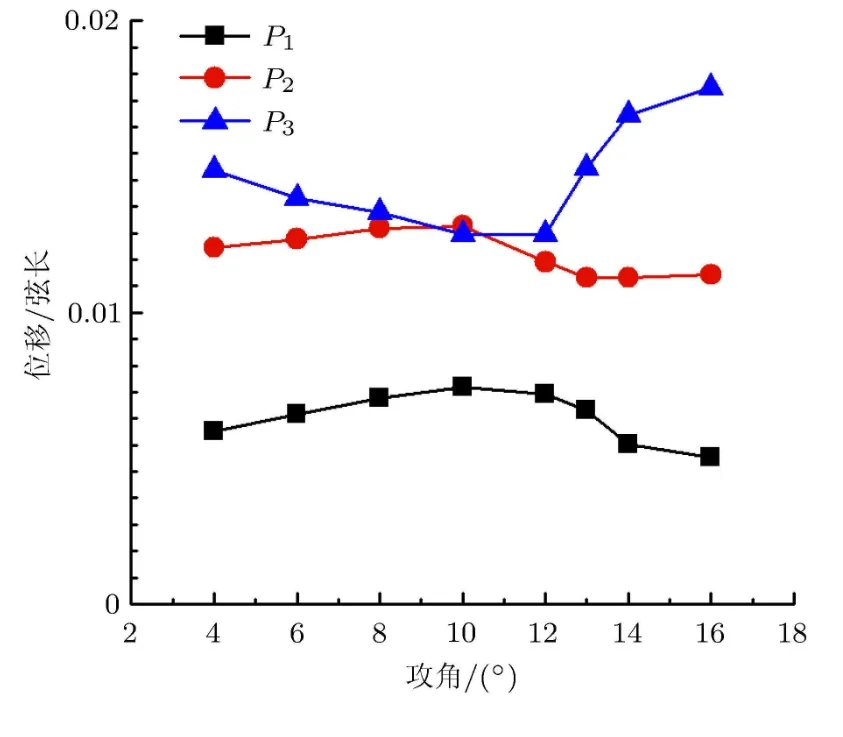
图8 不同攻角下各柔性段最大时均变形量

2.2 弹性模量的影响分析

弹性模量影响着材料的柔度，当柔性增大时，柔性结构在相同的气动力下将产生更大的变形，甚至产生大幅度的振动现象，从而影响周围流场.图9给出了雷诺数为135000、攻角为13◦时，不同弹性模量下的柔性翼型升力系数与时均升阻比.此时的刚性翼型的升力系数和时均升阻比分别为0.605和4.46.在弹性模量整个计算范围内，柔性翼型时均升力系数和升阻比相比刚性翼型都得到了明显的提高.当弹性模量为1MPa时，升力系数可以提高40%，升阻比提高了120%.一定程度上弹性模量越小，升力系数和升阻比越大.在弹性模量大于1.5MPa时，升阻力系数主要以定常为主.而当弹性模量小到一定程度时，升力系数将发生非定常波动，对翼型气动力的提升效果也有所减缓，弹性模量由1.5MPa减小为1MPa时升力系数和升阻比只分别提升了0.3%和0.5%.弹性模量进一步减小到0.7MPa时，升力系数波动幅度急剧增加，同时翼型的时均升力系数和升阻比反而呈下降趋势.

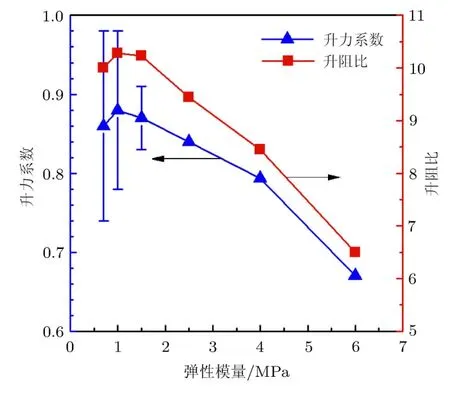
图9 升力系数和时均升阻比与弹性模量的关系

图10和图11分别给出了弹性模量分别为4MPa、1.5MPa和0.7MPa三种情况的近翼面时均流场图以及翼面时均压力分布.柔性翼面的变形作用使得吸力面的分离流再次附着，从而使得前半弦长吸力面压强减小，大幅度提高了柔性翼的升力系数.而当弹性模量由1.5MPa减小为0.7MPa时，翼面变形量的增加并不能使尾缘分离流附着，反而由于变形量过大，前缘刚性段与柔性翼面连接处的小涡尺度增大到一定程度使得前缘段流体附着面积减小(图10(c))，升力系数随着弹性模量的减小而减小.

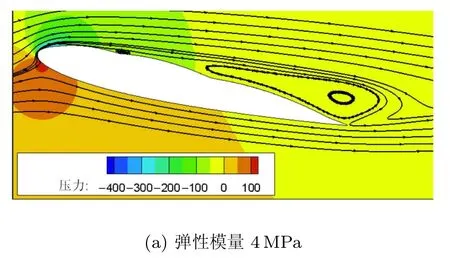
图10 不同弹性模量下近翼面流场图

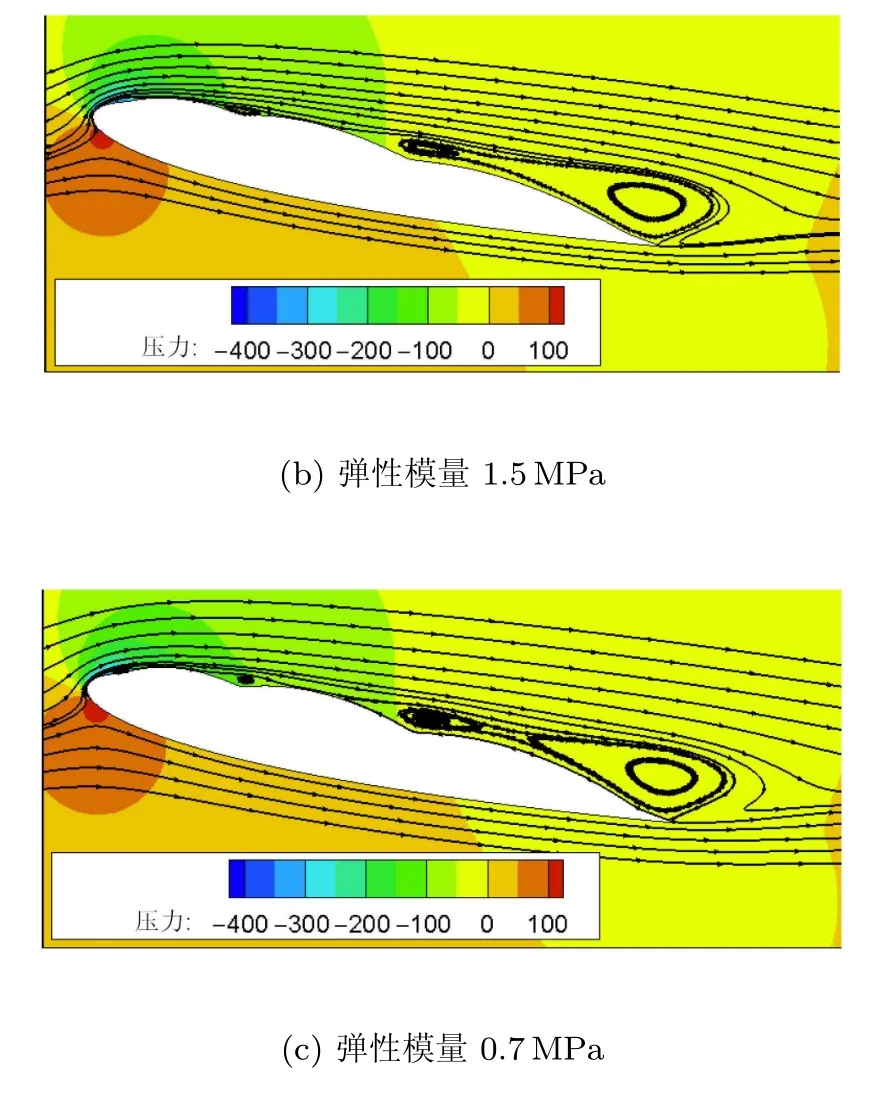
图10 不同弹性模量下近翼面流场图(续)

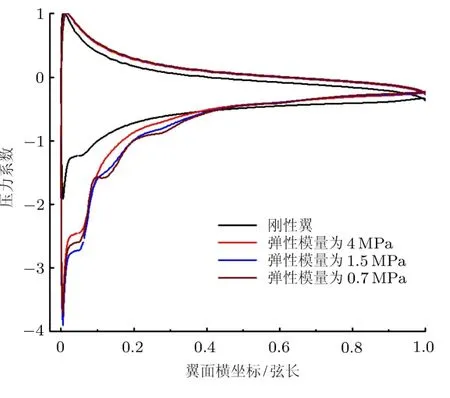
图11 不同弹性模量下翼面时均压力分布

图12给出的是三段柔性翼面中点P1,P2,P3在0.25s内的位移脉动情况.当弹性模型为2.5MPa时，三段柔性翼面的振动幅度是非常小的，此时翼型表面流场主要以定常为主.而当弹性模量减小到1.5MPa，此时三段柔性翼面发生了较大幅度的振荡，在中间翼面会卷起旋涡，翼面表面出现非定常流动现象.而当弹性模量进一步减小到0.7MPa时，三段翼面的振荡幅度急剧增加，前缘段柔性翼面的振动幅度相对较小，而中间柔性翼面的振荡幅度最大.翼型表面流场表现较强的非定常性，如图7所示.

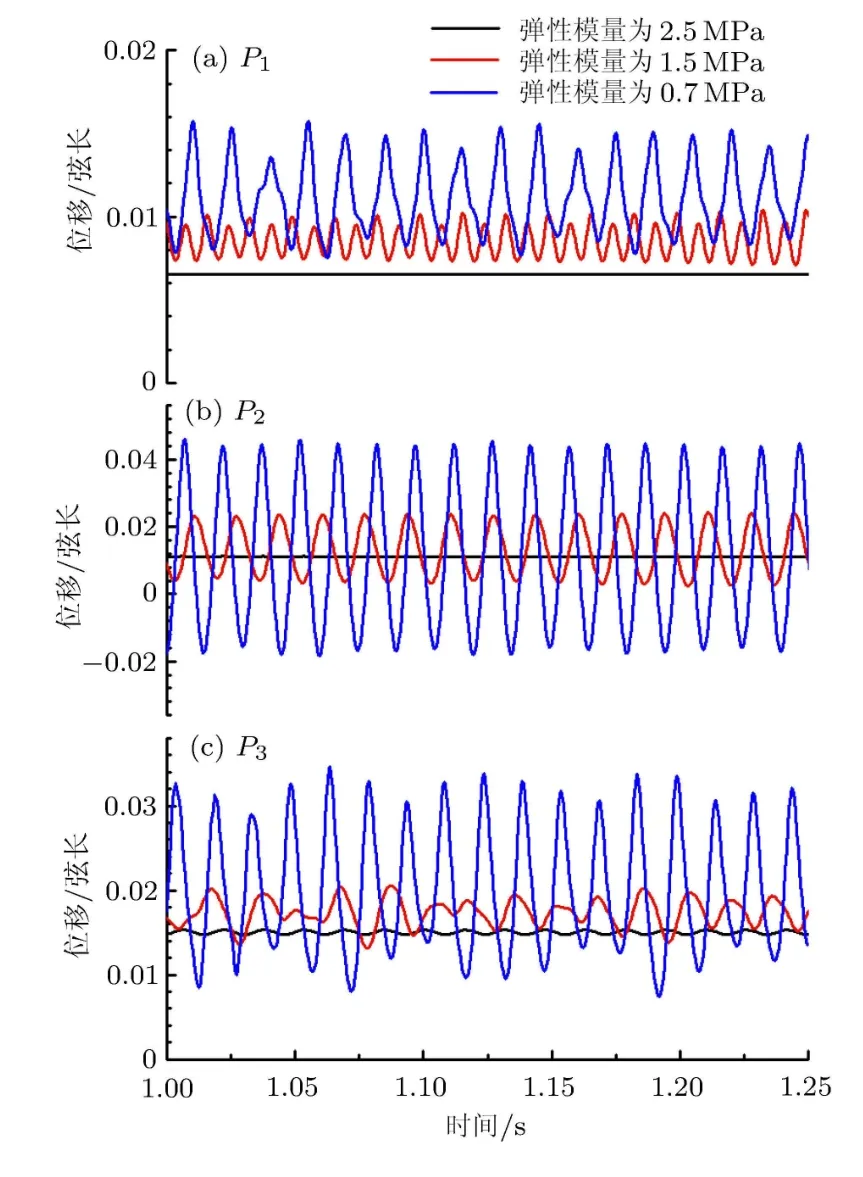
图12 柔性翼面中点位移时程线

图13给出的是不同弹性模量下三段柔性翼面的最大时均变形量与弹性模量的关系.时均变形量随着弹性模量的减小而增大，而且弹性模量越小，翼面变形量变化得越明显，即柔性较大时，对翼面变形的影响越显著.

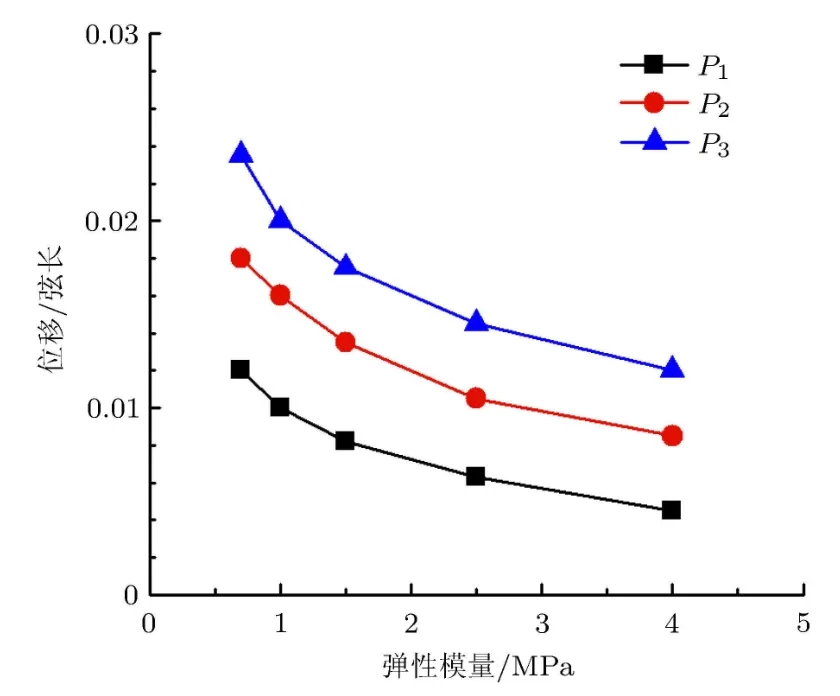
图13 不同弹性模量下各柔性段最大时均变形量

3 结论

本文采用流固耦合的方法对吸力面为三段柔性结构的翼型的绕流进行了数值模拟.研究了不同弹性模量下柔性翼的气动性能和翼面结构响应.研究结果表明：

(1)翼型柔性结构在气动力的作用下能够自适应变形，使得分离流再次附着，改变了翼型表面的流场结构，起到延缓失速和提高升力的作用.相比于刚性翼，升力峰值可提高4.7%，失速攻角拓宽2◦.

(2)失速后柔性翼的升力系数下降得较为缓慢，且柔性越大，升力系数下降得越平缓.减小弹性模量能够提高大攻角下的气动性能，然而弹性模量过小反而不利于翼型气动力的提升，并且会使得翼面产生大幅度的振动.

1 Bishop KL.The relationship between 3-D kinematics and gliding performance in the southern fl ying squirrel,Glaucomys volans.Journal of Experimental Biology,2006,209: 689-701

2 Waszak RM,Jenkins NL,Ifju P.Stability and control properties of an aeroelastic fi xed wing micro aerial vehicle.AIAA Atmospheric Flight Mechanics Conference and Exhibit,Montreal,Canada,2001

3 Wu CJ,Xie YQ,Wu JZ.“Fluid roller bearing”e ff ect and fl ow control.Acta Mechanica Sinica,2003,19(5):476-484

4 Curet OM,Carrere A,Waldman R,et al.Aerodynamic characterization of wing membrane with adaptive compliance.54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics,and Materials Conference,Boston, Massachusetts,2013

5 Gabor OS,Koreanschi A,Botez RM.Low-speed aerodynamic characteristics improvement of atr 42 airfoil using a morphing wing approach.IECON 2012-38th Annual Conference on IEEE Industrial Electronics Society,Montreal, 2012

6郭秋亭，张来平，常兴华等.多段翼型局部主动变形流动控制的非定常数值模拟.空气动力学学报,2011,29(5):607-612

7康伟，张家忠.翼型局部弹性自激振动的增升减阻效应研究.西安交通大学学报,2011,45(5):94-101

8 Dong HF,Wang CX,LI SB,et al.Numerical research on segmented fl exible airfoils considering fl uid-structure interaction.2014 Asia-Paci fi c International Symposium on Aerospace Technology,Shanghai,2014

9 Rojratsirikul P,Wang Z,Gursul I.Unsteady fl uid-structure interactions of membrane airfoils at low Reynolds numbers.Experiments in Fluids,2009,46(5):59-872

10 Lee T,Gerontakos P.Investigation of fl ow over an oscillating airfoil.Journal of Fluid Mechanics,2004,512:313-341

(责任编辑:刘希国)

THE AERODYNAMIC PERFORMANCE OF A FLEXIBLE AIRFOIL AT LOW REYNOLDS NUMBER1)

TAO Zhenxin∗,2)LI Shaobin∗,†,3)SONG Xizhen∗∗(National Key Laboratory on Aero-Engines,School of Energy and Power Engineering, Beihang University,Beijing 100191,China)
†(Collaborative Innovation Center for Advanced Aero-Engine,Beijing 100191,China)

A two way fl uid-structure interaction method is employed to simulate the aerodynamic performance and the structural response of NACA0012 airfoils,with three fl exible structures on a portion of the upper surface extending from 5%to 95%of the chord from the leading edge.The impact of the elastic modulus is analyzed. It is indicated that at a large angle of attack the deformation of the fl exible surface a ff ects the unsteady fl ow fi eld around the airfoil,delays the stall and improves the lift coefficient.Even when the stall occurs,the lift coefficient of the fl exible airfoil decreases more slowly with the increase of the angle of attack than that of a rigid airfoil.The fl exible airfoil with smaller elastic modulus has better aerodynamic performance.But too small elastic modulus is not conducive to the enhancement of the aerodynamic performance and the fl exible surfaces will experience a large amplitude vibration.

fl uid-structure coupling, fl exible airfoil,aerodynamic performance,deformation

V211.3

A

10.6052/1000-0879-16-258

2016–08–09收到第1稿，2016–10–09收到修改稿.

1)国家自然科学基金资助项目(51106003).

陶真新,李绍斌,宋西镇.低雷诺数下柔性翼型气动性能分析.力学与实践,2017,39(2):145-151 Tao Zhenxin,Li Shaobin,Song Xizhen.The aerodynamic performance of a fl exible airfoil at low Reynolds number.Mechanics in Engineering,2017,39(2):145-151