广义变分原理在求解杆系装配应力中的应用1)
2017-05-03谭邹卿杨云澜田玉祥蒋学东
谭邹卿杨云澜田玉祥蒋学东
(常州大学机械工程学院,江苏常州213164)
(江苏省绿色过程装备重点实验室,常州大学,江苏常州213164)
广义变分原理在求解杆系装配应力中的应用1)
谭邹卿2)谭邹卿,博士,讲师,主要从事固体力学的教学和应用研究.E-mail:zqtan@cczu.edu.cn杨云澜田玉祥蒋学东3)蒋学东,硕士,副教授,主要从事固体力学的教学和应用研究.E-mail:jxd3290294@cczu.edu.cn
(常州大学机械工程学院,江苏常州213164)
(江苏省绿色过程装备重点实验室,常州大学,江苏常州213164)
利用拉格朗日乘数法建立广义变分原理以求解有误差杆件结构装配应力.引入拉格朗日乘数并结合静力平衡方程,构造无条件广义变分原理的新泛函,求解新泛函的极值问题,获得超静定的变形协调方程,从而计算有误差杆件结构的装配应力.结果表明:该方法求解装配应力的通用性较强,不但克服传统几何方法建立变形协调方程的缺陷,而且具有计算过程简洁以及便于掌握等优点.
超静定,装配应力,广义变分原理,拉格朗日乘数法
加工构件时,构件的尺寸不可避免地存在微小误差.对静定结构,构件的加工误差只会造成几何形状的变化,不会产生内力.但在超静定结构中,若构件存在加工误差,在装配过程中将产生变形,从而存在附加应力,即所谓的装配应力.装配应力影响结构的承载能力,对于有误差杆系进行强度计算需考虑装配应力.材料力学教材[1]主要采用静力平衡方程、变形协调方程以及物理方程联立求解超静定问题.其难点在于如何补充变形协调方程.常用几何法分析超静定结构的变形,从而给出变形协调方程.但对于多杆系问题难以用几何法得出杆系变形的几何关系.为了解决这一困难,已有微分法[2]、节点位移法[3]、解析几何法[4]、矢量法[5]、力法[6]、功能原理[7]等对杆系超静定问题进行了探索.目前,少量文献基于广义变分原理研究了外载荷作用下超静定结构的内力[89]或库仑摩擦问题[10].然而,以上方法主要针对有外载荷情况下超静定问题的分析,对含误差杆系的超静定问题研究相对较少.另外,含误差杆系在装配完成后只有内力间的平衡,属于无外载情况下的超静定问题.因此,现有广义变分原理[810]不能直接求解杆系的装配应力.本文采用拉格朗日乘数法,建立有误差杆件结构的广义变分原理,构造相应的新泛函,以分析各杆的装配应力.
1 含误差杆件结构的广义变分原理
考虑有n+m个杆件的线性超静定桁架结构,各杆的弹性模量分别为Ei(i=1,2,···,n+m),横截面面积分别为Ai(i=1,2,···,n+m),杆件名义长度分别为li(i=1,2,···,n+m).假设超静定桁架中有一根杆尺寸相比名义尺寸存在加工误差,其误差长度为Δ.假设在装配后各杆的内力分别为Ni(i=1,2,···,n+m).为了便于讨论,令Ne为有误差杆的装配内力.
对n+m个杆件系统列出m个静力平衡方程
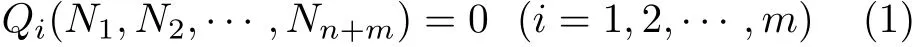
上式平衡方程仅与各杆的最终内力有关,与装配方式无关.
在线弹性范围内,整个杆系的应变能为
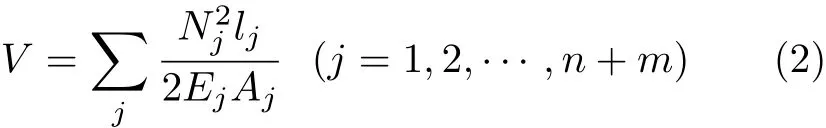
值得注意的是,静力平衡方程式(1)和整个杆系应变能式(2)与加工误差无关,不能直接利用式(1)和(2)分析加工误差效应.为了在满足平衡方程式(1)的条件下引入加工误差效应,本文构造一个无条件广义变分原理的新泛函为

其中,λi(i=1,2,···,m)为拉格朗日乘子.等式右边的第2项±ΔNe为考虑加工误差的势能,反映了加工误差效应的影响.计算时若取Ne为拉力,杆件加工尺寸比名义尺寸长时取“+”号,短时取“-”号.反之亦然.当Δ=0时,式(3)可解决无加工误差的超静定问题.
将Nj及λi都当作独立的变量进行变分,则当新泛函L达到极值时,利用式(2),则有

由于δNj及δλi都是独立的,因此L的极值条件为

其中,式(5)有m个方程,即为静力学平衡方程,而式(6)有n+m个方程,它等价于变形协调方程,所以总共有n+2m个方程,可解出n+m个内力Nj和m个拉格朗日乘子λi,从而可求装配应力.由此可见,基于无条件广义变分原理构造的新泛函极值问题等价于求解杆系超静定的三大基本方程.因此,该方法不需要求解变形协调的几何条件,使得计算过程变得简便且易掌握.
2 算例
算例1如图1(a)所示1和2两杆的刚度同为E1A1,3杆为E3A3.3杆的长度为l+Δ,其中Δ为加工误差.试求3杆装入AC位置后,三杆的轴力.

图1
对节点A进行受力分析,并假设各杆轴力均为拉力,如图1(b)所示.因结构和载荷均对称,则N1=N2,静力平衡方程为

由式(3),注意到杆3的尺寸比名义尺寸长,可构造的新泛函为

由式(6)并注意到l1=l/cosα,可得

由式(9)和式(10)消去λ得

上式即为变形协调方程.
由式(7)和式(11)可得各杆的轴力为
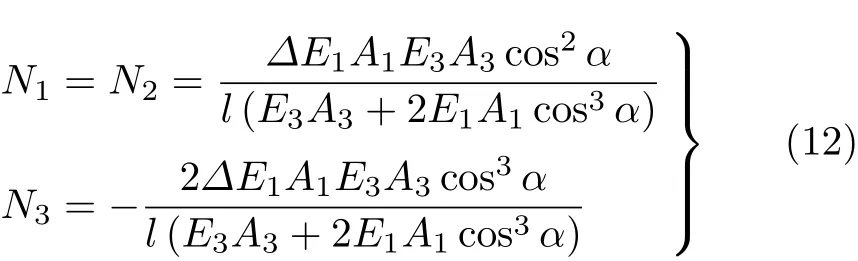
其中,负号说明杆3受压力.上式与几何法[1]等计算结果完全一致,验证了该方法的正确性.
算例2如图2(a)所示杆系,杆6比名义长度略短,误差为Δ,杆的刚度同为EA.试求将杆6装配到A,C之间后各杆的内力.

图2
假设各杆轴力均为拉力,节点A的受力图如图2(b)所示,平衡方程为

因结构和载荷均对称,所以

由式(3),注意到杆6的尺寸比名义尺寸短,可构造的新泛函为

上式求极值可得
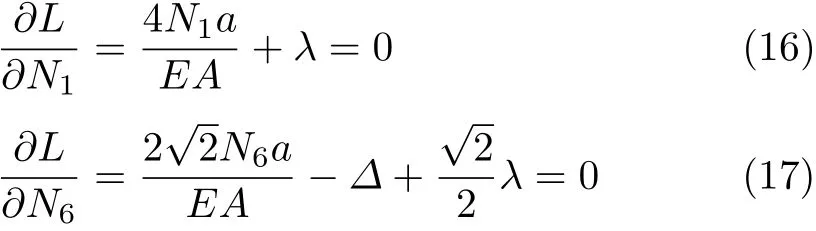
由式(16)和式(17)消去λ得

上式即为变形协调方程.
由式(13)、式(14)和式(18)可得各杆的内力为
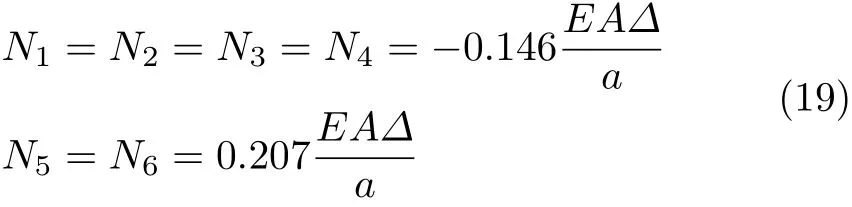
其中,负号说明杆1~4均受压力.上式与文献[1]的计算结果完全一致.
以上计算实例表明,在求解含误差杆件的超静定问题时,该方法求解过程简单方便,避免了建立变形协调几何关系的困难.
3 结论
本文构造了无条件广义变分原理的新泛函,利用求泛函极值问题,方便地解决含误差杆件结构的装配应力问题.该方法通用性较强,并且计算过程便于程序化,有利于求解复杂超静定结构的变形协调方程.利用同一思路,还可以解决温度变化等作用下的超静定问题.
1刘鸿文.材料力学(I)(第5版).北京:高等教育出版社,2013
2吴泽艳,王兴霞.平面汇交二力杆系变形协调条件的解析方法.力学与实践,2016,38(4):451-452
3陈平,陈国良,杨绪普.载荷作用下多杆汇交问题的通解.力学与实践,2014,36(3):348-350+378
4周道祥.解析法解杆系拉(压)超静定问题.力学与实践,2004, 26(2):66-67
5苏少卿,王销钧.小变形轴力杆件的变形位移方程.力学与实践,2011,33(4):74-77
6王钟羡.建立超静定杆系变形协调方程的能量方法.力学与实践,1998,20(6):55-56
7李丽柏.拉压弹性杆系小变形计算方法研究.力学与实践,2014, 36(4):474-477
8成祥生.结构分析中的广义变分原理及其应用.应用数学和力学,1985,6(7):639-646
9吴晓.拉格朗日函数法在静不定结构内力计算中的应用.空间结构,2016,22(1):25-30
10 Steiner W.The use of Castigliano’s theorem in Coulomb friction problems.Acta Mechanica,2014,225(9):2471-2483
(责任编辑:胡漫)
TB121
A
10.6052/1000-0879-16-208
2016–06–24收到第1稿,2016–10–27收到修改稿.
1)常州大学校基金资助项目(ZMF14020058).
谭邹卿,杨云澜,田玉祥等.广义变分原理在求解杆系装配应力中的应用.力学与实践,2017,39(2):202-205 Tan Zouqing,Yang Yunlan,Tian Yuxiang,et al.Application of generalized variational principle for solving assembly stress of rod system.Mechanics in Engineering,2017,39(2):202-205
