间接测量质量试验的可靠性及数据精度

尤明庆

(河南理工大学能源科学与工程学院，河南焦作454010)

间接测量质量试验的可靠性及数据精度

尤明庆1)E-mail:youmq@hpu.edu.cn

(河南理工大学能源科学与工程学院，河南焦作454010)

试验是确认科学知识正确与否的重要手段，贯穿于力学的理论研究和工程应用之中.通过测量排水体积和单摆周期,间接测量铁块质量，讨论试验设计和数据处理及其相关问题.

试验可靠性，数据精度，单摆，浮力

试验是建立和检验自然科学如物理知识的重要手段.费恩曼认为“数学不是科学，因判断其对错不需要试验”；当然，“if a thing is not a science,it is not necessarily bad.For example,love is not a science”[1].不过，现今中文语境下的“科学”已经不完全等同于英文的science.

力学以物理为基础、以数学为工具，研究物体的受力以及运动、变形和破坏，具有科学和技术的双重特征，已成为天文、地质、机械、建筑、水利等学科的基础[2].试验贯穿于力学的理论研究和工程应用[3]，相关学会或组织制定有各种力学试验规程，且进行补充、修订.

可靠的试验能够准确反映系统参数之间的关系，测试数据具有分析或判断所需要的精度.文献[4]提出间接确定物体质量的方法，学习之后颇有收益，不揣浅陋而赘述几句.

1 试验设计和测试方法

如图1所示，用篮球与网兜将铁块悬浮于水中，利用细绳测量水位变化La以及中间部位的周长Le,放大La到Ld=nLa，n=14,以细绳与螺母构成单摆，测量k=50个周期的时间Te和Td,计算水体即铁块的质量[4]

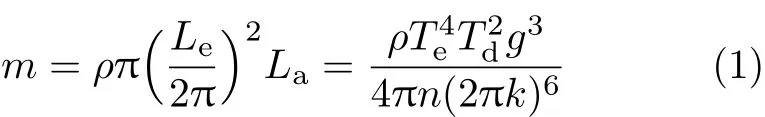
式中,水密度ρ=1000kg/m3，重力加速度g= 9.8m/s2.

文献[4]“实测铁块质量的典型数值Td=62.47s和Te=95.37s得m=1.797kg，而铁块的实际质量为1.80kg,两者之间的相对误差仅0.16%.经过多次实验发现，测试结果的重复性很好”，但没有给出重复试验结果或相关平均值和方差.不仅如此，计算排水体积应测试水桶内周而不是外周，文献[4]没有说明如何以细绳量测内周.

图1 利用浮力定律以及单摆周期测量物体质量[4]

或许可对测试方式略作改进.以直径20cm的平底锅分别承载铁块和水体，确定浮在直径略大容器中的水位；只要两种情形的水面高度相同，则水体质量与铁块相同.再依据浮力定律，锅内水体与其引起的排水增加相等；而锅保持直立姿态，可测量其外周和吃水变化计算排水体积.

另一种可行方法是，直杆支承在中点附近，两端分别悬挂直径20cm的平底锅，一侧置入铁块，另一侧添水至平衡而作为“秤砣”；取出铁块而加水至平衡；该水量以前述排水方法确定其体积.这可方便地重复称量以倍增水量而提高吃水深度的测试精度.不过，需要说明的是，这里只是铁块与水的等量置换，并不运用杠杆原理进行计算；正如曹冲称象也只是化整为零的等量置换，并无关乎浮力定律.

2 随机误差和系统误差

文献[4]的测试系统中，篮球周长为75cm，水桶直径应大于25cm；水深1cm的体积为500cm3，因而1.80kg物体引起的水位变化小于36mm.标志线的宽度、钉子以及细绳的直径(图1)均在1mm尺度；综合考虑，水位变化La的测试误差在1mm左右，即相对误差可达到3%.

数字式秒表尽管读数精度可达0.01s，但人的反应时间在0.15s左右.这可以拇指和食指捕捉从静止降落的钢尺或纸币确认.时间测量的误差大约在1%量级，而以式(1)计算质量时则放大到5%左右.利用手机的视频功能测量时间似可提高精度.

以上长度和时间的误差是直接测试过程中引起的，其正负和大小具有不确定性，称为随机误差或偶然误差，可以通过重复测试求取平均值而减小.另一类误差是试验系统本身所具有的，需要在分析研究之后对计算结果进行具体修正.略作说明如下.

单摆并不真正具有等时性，其周期与摆角β相关摆角为10◦,20◦和30◦时，周期的修正项达0.19%, 0.76%和1.71%，式(1)给出的质量与周期的6次幂相关，因而修正因子为0.989,0.956和0.903.不过，测试摆角过小，则因空气阻力而难以连续测量数十个周期，且摆幅及速度较小而不利于确定完整周期的位置.似可适当增大摆角至20◦左右而测试10～20个周期较好，当然应基于式(2)对周期进行修正以减小误差.

因地球自转产生的离心力等原因，重力加速度g也会随纬度变化，如在广州和北京分别为9.788m/s2和9.801m/s2；水的密度也会随温度变化，25◦C时为997.0kg/m3，而低于10◦时为1000.0kg/m3.

水面处篮球截面不同，表面张力也将引起排水体积的计算差异；此外，如果文献[4]只是以细绳测量水桶外周，则需要基于水桶壁厚进行修正.细绳通常在受力之后略有伸长，其悬挂摆锤后的长度对应于基于测量周期计算所得结果.

3 有效数字和数据精度

文献[4]选取的重力加速度、密度只有2～3位有效数字，或许最终计算结果m=1.797kg可保留3位数字即小数两位；而实际铁块质量1.80kg意味着1.795～1.804kg，即测试结果并非误差1.6‰,而是“绝对精确”.家用杆秤的分辨率多是半两即0.025kg，精度更低.

手工计算时总是不断地确定有效数字以提高效率，而计算机采用的数字是额定位数，但对最终结果最好依据有效数字适当截取.文献[5]试验参数(相当于自变量)的有效位数不超过3位，其表3中频率134.6832Hz和载荷147.1802kN这样的数值，最多保留小数1位即可.这也便于阅读和比较.

就笔者所知，试验设备的测量精度通常在1‰的量级，因而数据一般可取4位数字，如人的身高只需精确到mm；昔日《常用数学用表》也多是4位数，如以及lg2=0.3010, lg3=0.4771.就此而言，现在有计算机，圆周率宜取为5位数字的3.1416而非3.14，使其完全不影响计算精度——后者可引起式(1)计算结果因圆周率7次幂而偏大3.6‰.当然，例外情形总是存在的,如天文观测以及密立根测量带电油滴运动[6]，其确定电子的电荷数值为(1.603±0.002)×10−19C，相关数据具有较高精度而保留了更多数字.

公元前225年埃拉托斯芬发现，夏至正午太阳与埃及亚历山大城的垂直方向成7.2◦，而在其南方500英里的塞尼(今阿斯旺大坝处)却直射枯井，可得地球半径4000英里；公元前130年古希腊的伊巴谷依据月全食时间推算地球本影在该处的弧长相当于2.5倍月球直径，确定地月距离236000英里.两者与现代测试值3986英里和240000英里相差无几[7].不过，所涉测量数据精度较低，如此美好的计算结果只是幸运；而确定地月距离所需要的最长月全食时间可不容易得到呢.此外，某些远高于测试精度的“原始数据”或过于理想的“试验结果”，可能缘于相关知识的欠缺而编造不当，将其应用于工程设计是危险的[8].

间接测量可能增加误差，如以分辨率0.1kg的电子秤为婴儿称重(表1).原始数据误差±0.05，婴儿体重误差±0.10，而周增重误差则达到±0.20.表中“真重”是设想的数值以说明计算可能引起的误差.

表1 以提篮间接称重婴儿(单位：kg)

尽管婴儿每周规则增重0.20kg，但基于间接称量得到的结果可以是0.0,0.1,0.2,0.3或0.4kg，最大差别达到0.4kg即8两.显然，基于两次称量值相减而得到的婴儿体重是可靠的，尽管稍有误差；但周增重已完全失真.相关结论是数值计算的常识，只是我们临事慌乱而忘了.或许，婴儿生长具有较大波动并非真实而可能源于间接测量所引起的误差.就此也可以理解惠斯顿电桥的巧妙设计和特别价值：以两臂中间的电压差直接表征120 Ω应变片的电阻微小变化，并不测量应变片电阻的绝对数值[9].

在不能提高电子秤精度的制约下，可进行重复测试：在提篮中添加不同衣物后多次称量，将得到2个婴儿体重数值：W和W+0.1，其变化范围0.1kg是测试误差，而婴儿体重估计为W+0.05(图2),误差可减小到±0.05kg而与电子秤的分辨率相当.与此相应，周增重的误差将减小到±0.1kg.

随机设计提篮重量而进行大量测试，若婴儿体重W出现的次数显著多于W+0.1的次数，则判断婴儿体重低于W+0.05而估计为W+0.025；反之则为W+0.075;若两者没有明显区别，则确认体重为W+0.05.婴儿体重误差将降低到±0.025kg，周增重的误差则减小到±0.05kg，即达到电子秤的精度.相关统计分析或可靠性判断[9]不再赘述.

图2 婴儿体重的间接称量及3个估计值

4 结语

试验对力学至关重要.在理论分析后设计试验以准确可靠地反映系统参数之间的关系，测试方法应具有较高分辨率以保证数据精度.如伽利略所论证，掺银30%的金冠和等重黄金分别置入直径20cm水盆，水位升高值仅相差0.4mm，难以区分两者体积的异同，而以溢出法测量体积则受到水表面张力的影响，均不能确定金冠掺杂与否；可行的方法是确定两者在空气和水中能否使相同力臂的杠杆保持平衡.

许多环境因素如地理位置、温度等对试验结果都有不同程度的影响，而公式及参数取值通常只在一定范围或精度内正确；最好在具体分析之后进行适当修正以消除系统误差，并对重复试验结果进行统计分析而减小随机误差.

试验数据总是具有一定的误差，而误差可能在后续计算中放大；多次迭代计算可以使最终结果完全失真[1011].就此而言，对间接测试结果的精度或误差应持谨慎态度，更不能从大量离散的数据中挑选个别“典型试验结果”进行计算以确认研究的可靠性.

1费恩曼RP，莱顿RB，桑兹M.费恩曼物理学讲义(第1卷).郑永令，华宏鸣，吴子仪等译.上海：上海科学技术出版社,2005. 1,22

2尤明庆.力学的定义.http://blog.sciencenet.cn/blog-275648-747329.html

3武际可.力学史.上海：上海辞书出版社，2010

4杨汉文,李国清,张一帆.间接测量质量、长度和时间的趣味力学实验.力学与实践,2016,38(3):317-320

5丁智平,方建辉,卜继玲等.橡胶弹性支座动态承载特性及其影响因素分析.力学与实践,2015,37(4):492-498

6 Olenick RP,Apostol TM,Goodstein DL.力学世界.李椿，陶如玉译.北京：北京大学出版社,2002.161-1637弗伦奇AP.牛顿力学(第2册).郭敦仁，何成钧译.北京：人民教育出版社,1982.75-77

8尤明庆.对锚固体强度强化理论的讨论.岩石力学与工程学报，2014,33(5):1075-1077

9张明，苏小光，王妮.力学测试技术基础.北京：国防工业出版社,2008.12-41,60-70

10尤明庆．割圆术确定圆周率方法的改进——祖冲之确定圆周率过程之猜测.安阳师范学院学报，2003,(2)：11-12

11尤明庆.单参数的正则抛物线准则.岩石力学与工程学报，2012, 31(8)：1580-1586

(责任编辑:胡漫)

O3

A

10.6052/1000-0879-16-290

2016–09–06收到第1稿，2016–10–21收到修改稿.

尤明庆.间接测量质量试验的可靠性及数据精度.力学与实践,2017,39(2):205-207,195 You Mingqing.Test reliability of indirect measurement for mass and the accuracy of data.Mechanics in Engineering, 2017,39(2):205-207,195