基于REV尺度格子Boltzmann方法的页岩气流动数值模拟

张烈辉 贾鸣郭晶晶

(西南石油大学石油与天然气工程学院，成都610500)

基于REV尺度格子Boltzmann方法的页岩气流动数值模拟

张烈辉 贾鸣1)E-mail:2585119904@qq.com郭晶晶

(西南石油大学石油与天然气工程学院，成都610500)

结合页岩扫描电镜图像，提出页岩气藏物理模型，采用表征单元体积(representative elementary volume,REV)尺度格子Boltzmann方法，考虑滑脱效应，模拟页岩气在页岩气藏中的流动.模拟结果表明，页岩气主要沿着天然裂缝窜进，但在有机质和无机质中也存在缓慢的流动，且有机质中的流速要略大于无机质中的流速.通过改变地层压力，研究地层压力对页岩气渗流特性的影响.研究结果表明，整个流场的速度和渗透率均随着地层压力的下降而增加.

格子Boltzmann方法,表征单元体积尺度,滑脱效应,页岩气,数值模拟

随着常规油气资源的减少和非常规资源开采技术的提高，页岩气在油气田开发领域扮演的角色越来越重要[14].据前人研究表明，页岩气藏主要由基质(有机质、无机质)和天然裂缝组成，且绝大部分有机质和无机质中的孔隙均为纳米级孔隙[5].页岩气在这样微小孔道中流动，常常由于较大的克努森数而引起气体分子在固体表面滑脱，从而引起滑脱效应.研究滑脱效应对页岩气渗流影响对于页岩气藏的理论研究和工程实践都具有重大的意义.

页岩气的流动数值模拟常常分为三个尺度：孔隙尺度，表征单元体积(representative elementary volume,REV)尺度和油田尺度[67].通常，在REV尺度上，基于控制偏微分方程的离散数值方法常被用来研究流动过程.孔隙尺度方法包括格子Boltzmann方法和直接蒙特卡洛方法.由于格子Boltzmann方法具有编程简单，易于并行计算，且能够处理复杂边界条件的优点，近几年在页岩气数值模拟研究领域得到广泛的应用[8].但是，如果将孔隙尺度的格子Boltzmann方法直接运用到REV尺度上，计算量将会巨大[9].因此，研究REV尺度的格子Boltzmann方法具有很大的工程运用价值.

本文基于Guo等[7]提出的REV尺度格子Boltzmann方法，考虑滑脱效应，研究页岩气在页岩气藏中的渗流特性.考虑实际生产过程中气藏压力不断下降，本文还将研究压力对页岩气藏渗流特性以及全局渗透率的影响.

1 考虑滑脱效应的页岩气流动控制方程

Nithiarasu等[10]最初提出均质多孔介质瞬态渗流的Brinkman--Forchheimer--Darcy模型，后来Gao等[11]为了研究具有非均质性的多孔介质渗流问题，对上述模型进行了修正，提出了非均质模型.由于页岩气藏可以看作是由有机质、无机质和天然裂缝组成的非均质场，故本文采用Gao等[11]的非均质模型，其二维渗流的宏观控制方程可以写成

式中，▽2为拉普拉斯算子；u为流体的体积平均速度；t为时间;φi为第i个成分的孔隙度；ρ为流体密度；p为流体压力；υe为有效黏度；F为流体在多孔介质中所受的合力，包括线性项、非线性项和体积力项.为考虑页岩气藏中气体流动的滑脱现象，在Gao的模型中引入视渗透率计算阻力

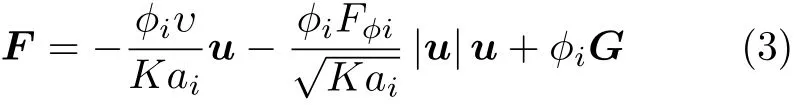
式中，υ为流体黏度，常与有效黏度υe取为相等；Fφi为多孔介质的几何形状因子

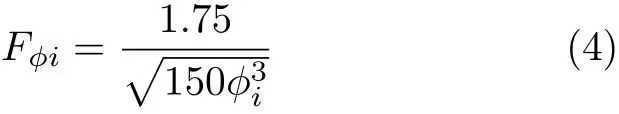
Kai为第i个成分考虑滑脱效应后的视渗透率，它与由多孔介质结构决定的绝对渗透率Ki和克努森数Kn有关.其中，第i个成分的绝对渗透率Ki根据Kozeny--Carman(KC)方程[12]计算

其中，C为KC常数，由多孔介质的固体颗粒直径确定.根据Klinkenberg滑脱定律，视渗透率Ka为绝对渗透率K和滑脱因子fc的乘积.在本文中，滑脱因子fc由克努森数Kn确定，采用具有二阶精度的Beskok--Karniadakis修正关系[13]计算

式中的b为滑移系数，稀疏因子α(Kn)采用Civan[14]提出的关系式计算

2 格子Boltzmann模型

本文采用Qian等[15]提出的D2Q9(二维九速)模型进行计算.流体的密度分布函数fi(r,t)在格子空间的演化方程如下

式中，fi(r,t)为t时刻在格点r处沿i方向的流体密度分布函数；△t为格子空间的时间步长；τ是弛豫时间；ei为格子空间的离散速度，在D2Q9模型中，其表达式如下

式中c为格子速度，其值为格子步长和时间步长的比值，通常取为1.式(8)中为平衡态分布函数，在D2Q9模型中，当考虑孔隙度的非均质性时，计算如下

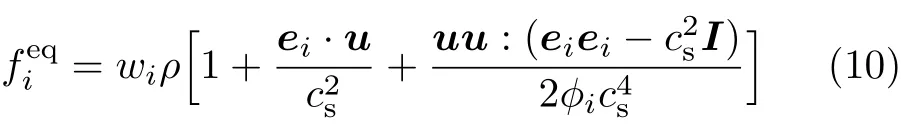
式中，wi为加权系数，并有w0=4/9，w1−4=1/9，w5−8=1/36；cs为格子声速，且=c2/3；I为单位矩阵.Fi为外力在格子空间的离散项，本文依然采用Guo等[7]给出的表达形式

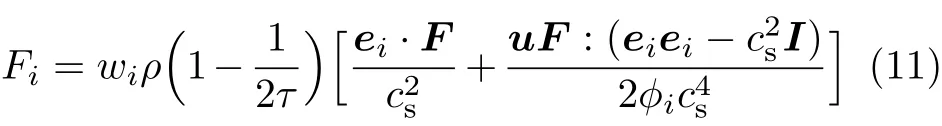
物理空间和格子空间之间的联系由宏观密度、宏观速度和流体密度分布函数之间的关系体现，表示如下

根据式(3)可知，外力F的求解包含速度u，因此式(13)是一个非线性方程.Guo通过引入中间变量V，成功地给出了速度u的计算表达式，具体推导过程参考文献[7].

3 算法验证

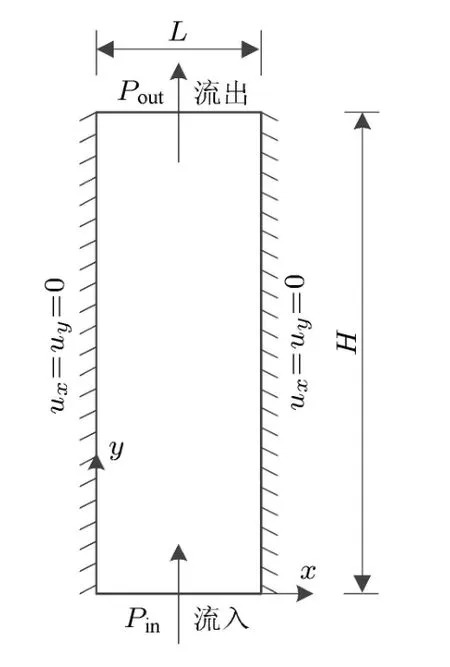
图1 经典Poiseuille流模型示意图

为了验证本数值算法的可靠性，本文采用文献[16]中的计算模型和计算参数，模拟压力作用下的经典Poiseuille流.文献[16]中的模型如图1所示，无量纲计算参数如下(计算量均为格子单位)：计算区域为L×H=200×50；孔隙度φ=1.0；渗透率K=∞；出入口压力p由密度ρ确定，ρin=1.001，ρout=0.999；时间步长和格子步长均取一个格子单位；弛豫时间τ=1；左右边界均为不渗透边界(ux=uy=0)，在格子空间采用非平衡外推格式计算.当流场达到稳定的时候，绘制流场中间断面流速uy的分布图，并与经典理论解和文献[16]的结果对比.从图2中可以看出，本文数值算法与理论解，以及文献[8]的结果非常吻合，这验证了本数值算法的正确性.

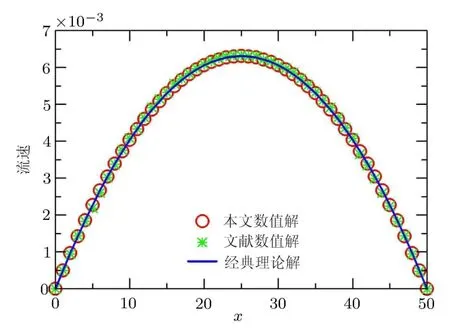
图2 两平板间y方向的速度剖面图

4 页岩气流动模拟

4.1 页岩气渗流场分析

对某地区的页岩岩心用扫描电镜扫描，得到分辨率为5µm的图像(图3).从图中可见，天然裂缝的宽度也不过在100nm左右.为了更好地研究页岩气在有机质、无机质和天然裂缝中的渗流情况，本文根据图3提出了页岩气渗流多孔介质模型(图4，红色表征天然裂缝，绿色表征有机质，蓝色表征无机质).

图3 页岩扫描电镜图

图4 页岩多孔介质模型图

对图4模型中的有机质、无机质和天然裂缝分别赋予不同的孔隙度，然后进行格子Boltzmann数值模拟.其中，有机质孔隙度φom=0.03，无机质孔隙度φim=0.01，裂缝的孔隙度φf=0.1.其余的参数设定如下：计算区域为170µm×200µm；流体沿y正方向流动，在入口处的压力pin=15.15MPa,出口的压力pout=14.85MPa,其余区域压力为pres= 15MPa，上下边界为定压边界，左右边界为封闭边界；温度T=323K；流体黏度υ=1.4×10−5Pa·s；气体常数R=8.314J/(mol·K)；页岩气相对分子质量Mr=16；克努森数Kn由分子平均自由程和有效孔隙半径的比值确定；每个区域的视渗透率按照式(5)～式(7)确定.

当计算达到收敛时，整个流场的速度场如图5所示，可以看出，流体主要是沿着天然裂缝流动，在有机质和无机质中也存在缓慢流动.为了更好地区分流体在有机质和无机质中的差别，本文绘制了流速的等值线图，如图6.在等值线图中，流速越大，等值线越密集，因此，流体在有机质中的流速要稍微大于无机质中的流速.图7为y=146µm截面的速度剖面分布图，其中，在4µm≤x≤28µm和141µm≤x≤150µm为有机质，在60µm≤x≤65µm为天然裂缝，其余为无机质.该图也印证了流体主要沿着天然裂缝窜进，在有机质中的速度略大于无机质中流速这一结论.

图5 流场稳定时速度分布场图

图6 流场稳定时速度等值线图

4.2 地层压力对流速和全局渗透率的影响

在页岩气藏的开采过程中，地层压力会随着开采过程而逐渐降低，因此很有必要研究地层压力对渗流特性的影响.在4.1节给出的计算参数中，仅仅改变地层压力和进出口压力，但保持压差不变，其余参数均不改变，计算y=146µm处的速度剖面图和全局渗透率.全局渗透率采用达西公式计算，即根据达到稳定后出入口的流量和压差计算.图7为地层压力取5MPa，10MPa，15MPa和20MPa时y=146µm处的速度剖面图，从图中可以得出，当压力逐渐减小的时候，各处的速度均在增大，这主要是因为压力减小，导致克努森数Kn增大，滑脱现象变得严重，从而导致了速度增加.滑脱现象严重化也导致了全局渗透率的增加，如表1.这表明，随着页岩气藏的开采，地层压力降低将导致滑脱现象愈发明显，从而导致全局渗透率增加.如果采用恒定的初始渗透率估算产量，将导致错误.

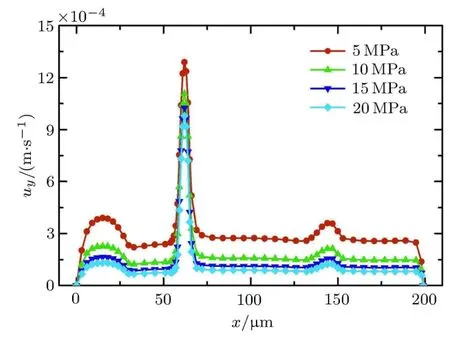
图7 不同地层压力下y=146µm处的速度剖面图

表1 不同地层压力下的全局渗透率

5 结论

(1)采用REV尺度的格子Boltzmann方法，考虑滑脱效应和储层非均质性，并考虑有机质、无机质和天然裂缝差异，提出了页岩气流动数值模拟算法，并用经典Poiseuille流动算例验证了算法的正确性.

(2)页岩气在页岩流动过程中主要沿着天然裂缝窜进，在有机质和无机质孔隙中也存在缓慢流动.随着地层压力的降低，整体速度都存在上升的趋势.

(3)随着页岩气的开采，页岩气藏的地层压力逐渐降低，这将导致地层中的克努森数增加，使滑脱效应变得严重，从而使整个储层的全局渗透率增加.如果采用初始的渗透率估算页岩气的产量，将导致错误.

1金衍，程万，陈勉.页岩气储层压裂数值模拟技术研究进展.力学与实践，2016，38(1)：1-9

2朱维耀，邓佳，杨宝华等.页岩气致密储层渗流模型及压裂直井产能分析.力学与实践，2014,36(2)：157-160

3郭为,胡志明,左罗等.页岩基质解吸–扩散–渗流耦合实验及数学模型.力学学报,2015,47(6):916-922

4朱光普,姚军,樊冬艳等.页岩气藏压裂水平井试井分析.力学学报,2015,47(6):945-954

5 Wang JJ，Chen L，Kang QJ，et al.Apparent permeability prediction of organic shale with generalized lattice Boltzmann model considering surface di ff usion e ff ect.Fuel，2016，181：478-490

6张潇丹，雍玉梅，李文军等.REV尺度多孔介质格子Boltzmann方法的数学模型及应用的研究进展.化工进展，2016，35(6)：1698-1712

7 Guo ZL，Zhao TS.Lattice Boltzmann model for incompressible fl ows through porous media.Phys Rev E，2002，66:036304

8张磊，姚军，孙海等.基于数字岩心技术的气体解析/扩散格子Boltzmann模拟.石油学报，2015，36(3)：161-365

9 Chen L，Fang WZ，Kang QJ，et al.Generalized lattice Boltzmann model for fl ow through tight porous media with Klinkenberg’s e ff ect.Phys Rev E,2015,91:033004

10 Nithiarasu P，Seetharamu KN，Sundararajan T.Natural convective heat transfer in a fl uid saturated variable porosity medium.International Journal of Heat and Mass Transfer，1997，40(16)：3955-3967

11 Gao JF，Xing HL，Tian ZW，et al.Lattice Boltzmann modeling and evaluation of fl uid fl ow in heterogeneous porous media involving multiple matrix constituents.Computers&Geosciences，2014，62：198-207

12 Carman PC.Fluid fl ow through granular beds.Trans Inst Chem Eng，1937，15:150-167

13 Beskok A，Karniadakis G.Report a model for fl ows in channels,pipes,and ducts at micro and nano scales.Microscale Therm Emg，1999，3(1)：43-77

14 Civan F.E ff ective correlation of apparent gas permeability in tight porous media.Transp Porous Med，2010，82：375-384

15 Qian YH，d’Humieres D，Lallemand P.Lattice BGK model for Navier--Stokes equation.Europhysics Letters，1992，17(6)：479-484

16申林方，王志良，李邵军.基于格子博尔兹曼方法表征体元尺度土体细观渗流场的数值模拟.岩土力学，2015，36(2)：689-694

(责任编辑:周冬冬)

NUMERICAL SIMULATION OF SHALE GAS FLOW BASED ON THE LATTICE BOLTZMANN METHOD AT REV SCALE

ZHANG LiehuiJIA Ming1)GUO Jingjing
(College of Petroleum Engineering,Southwest Petroleum University,Chengdu 610500,China)

During the seepage of the shale gas,its e ff ect is due to the large Knudson number,which makes the gas molecules slip from the solid surface.Based on the REV(representative elementary volume)scale lattice Boltzmann method,the fl ow of the shale gas is simulated with consideration of the slippage e ff ect.With the scanning electron microscope image,a physical model with organic rock,nonorganic rock and natural fractures is taken,and then the shale gas fl ow in the model is simulated.The simulated results indicate that the shale gas mainly fl ows in the natural fractures.However,the shale gas also fl ows slowly in the organic and nonorganic rocks,and the velocity in the organic rocks is larger than that in the nonorganic rocks.The in fl uence of the reservoir pressure on the shale gas seepage is also studied by varying the reservoir pressure.It is indicated that with the decrease of the reservoir pressure,the Knudson number increases and the slippage e ff ect intensi fi es, thus the velocity and the permeability of the whole fl uid fi eld increase.

lattice Boltzmann method,REV(representative elementary volume)scale,slippage e ff ect,shale gas,numerical simulation

TE371

A

10.6052/1000-0879-16-372

2016–11–15收到第1稿，2016–11–29收到修改稿.

张烈辉,贾鸣,郭晶晶.基于REV尺度格子Boltzmann方法的页岩气流动数值模拟.力学与实践,2017,39(2):130-134 Zhang Liehui,Jia Ming,Guo Jingjing.Numerical simulation of shale gas flow based on the lattice Boltzmann method at REV scale.Mechanics in Engineering,2017,39(2):130-134