早龄期混凝土抗裂性环形试验研究进展1)

王福禄 董伟袁文岩

(大连理工大学海岸和近海工程国家重点实验室，辽宁大连116024)

早龄期混凝土抗裂性环形试验研究进展1)

王福禄 董伟2)董伟，副教授，主要从事混凝土断裂机理的研究.E-mail:dongwei@dlut.edu.cn袁文岩

(大连理工大学海岸和近海工程国家重点实验室，辽宁大连116024)

早龄期混凝土极易在限制收缩条件下产生裂缝进而影响结构的安全性、耐久性和适用性，因此提供一种简单有效的方法来评估早龄期混凝土在限制收缩条件下的抗裂性，就显得非常重要.由于能够提供一定的约束刚度并易于实验室操作，限制收缩环形试验被广泛应用到混凝土在限制收缩条件下的抗裂性评估.主要从限制收缩环形试验的发展、破坏机理、影响因素三方面进行阐述.通过限制收缩环形试验进行不同目的的混凝土试验研究，推动了限制收缩环形试验的不断发展；破坏机理主要有最大拉应力理论以及基于断裂力学的断裂能机制预测混凝土的开裂；环形试验的影响因素主要有试件几何尺寸，边界条件，混凝土材料性能以及预制裂缝四个方面.最后介绍了一种椭圆环试验方法，可有效评估高约束度下混凝土的抗裂性.

早龄期混凝土,限制收缩,破坏机理,影响因素

引言

早龄期普通混凝土在自身水化反应、内部水分散失、外界温度变化等因素的影响下，其体积发生改变，当这种体积变化受到外部约束时，混凝土内部产生拉应力[1]，拉应力大于其本身抗拉强度时，可能会导致混凝土出现裂缝，从而降低混凝土结构物的承载能力、耐久性以及防水性，降低结构寿命，增加维护开支.尤其在一些扁平结构中混凝土的收缩裂缝是一个主要病害，例如：工业楼板、混凝土路面、桥面板等.为了解决混凝土工程中因早期裂缝引起的耐久性降低问题和结构失效，需要对早龄期混凝土的抗裂性能进行评估，并有针对性地改进其抗裂性能.

而采用怎样的试验方法评估混凝土的抗裂性，选择抗裂性满足工程条件的混凝土，是当前工程界与学术界共同关注的问题.在此背景下，推动了评估混凝土抗裂性试验方法的发展.目前常用的试验方法有自由收缩和限制收缩试验.自由收缩试验虽然能比较不同混凝土的体积变化，但难以评估材料在外部约束作用下的抗裂性能[2].限制收缩试验根据其提供约束方式的不同主要分为约束条形试验[3]，约束板式试验[4]，约束环形试验[5].虽然约束板式试验有很多优点，但它只能部分、不均匀地约束混凝土的收缩变形，裂缝的产生无规律，这些缺点使得约束板式试验无法精确地对混凝土抗裂性进行评价，不利于相互比较和标准化[6].由于试验方法相对比较经济、容易处理端部约束并易于实验室操作，目前限制收缩圆环试验被较为广泛地应用于混凝土在限制收缩条件下的抗裂性评估[5].美国国家公路与运输协会(American Association of State Highway and Transportation Officials,AASHTO)[7]及美国试验材料学会(American Society for Testing and Materials, ASTM)[8]将限制收缩圆环试验定为一种评估混凝土抗裂性的标准试验方法.此外，我国《混凝土结构耐久性设计与施工指南》[9]推荐限制收缩圆环试验法定为测试水泥基胶凝材料抗裂性的标准方法.

限制收缩圆环试件如图1所示，图中RIS,ROS, RIC,ROC分别表示钢环的内径、外径，混凝土环的内径、外径.试验过程如下：钢底板上套有两个不同内径尺寸的同心钢环，在两钢环之间进行混凝土的浇注、振捣、养护后拆掉外钢环得到所需试件，内环提供对外部混凝土的约束，混凝土收缩受到内环的约束产生拉应力，如果产生的拉应力超过混凝土自身抗拉强度便会开裂.AASHTO推荐的标准化试件参考尺寸为[7]：钢环内径305mm，内部约束钢环厚度12.3～13.1mm，外部混凝土环壁厚75mm，钢环高度152mm，试验养护温度19.3◦C～22.7◦C，相对湿度46%～54%，采用混凝土外圆周表面干燥的方式，在约束钢环的内壁中间位置沿环向粘贴应变片，应变片的示数出现突然地回滞标志着混凝土的开裂，如图2所示.由于AASHTO推荐的试件约束刚度较低，试验过程中可能会出现混凝土开裂时间过长甚至不开裂的情况[10]，不能有效地评估早龄期混凝土的抗裂性，ASTM建议将混凝土壁厚降低为37.5mm，以此来提高内部钢环的约束度[8].我国《混凝土结构耐久性设计与施工指南》[9]中推荐的试件尺寸为：内径41.3mm，外径66.7mm(壁厚即为25.4mm)，高度25.4mm.在试件顶面和底面涂抹隔离剂进行密封处理后放入恒温恒湿箱中，箱内控制温度19.5◦C～20.5◦C，湿度40%～60%.试件开裂时间为应变计显示减小上百个微应变或者增加数百个微应变的时刻.目前，限制收缩环形试验已被广泛应用于自密实混凝土[1114]、高性能混凝土[1,15-17]、超高性能混凝土[18-20]、超高性能纤维增强混凝土[2124]、轻骨料混凝土[2528]等抗裂性试验中.

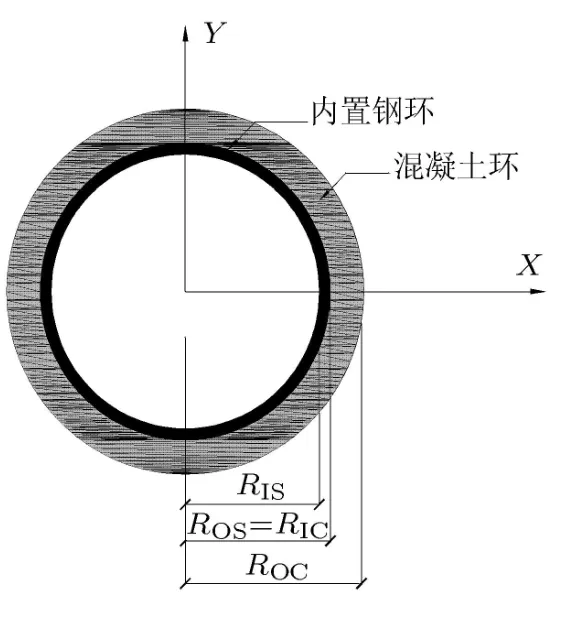
图1 混凝土限制收缩圆环试件

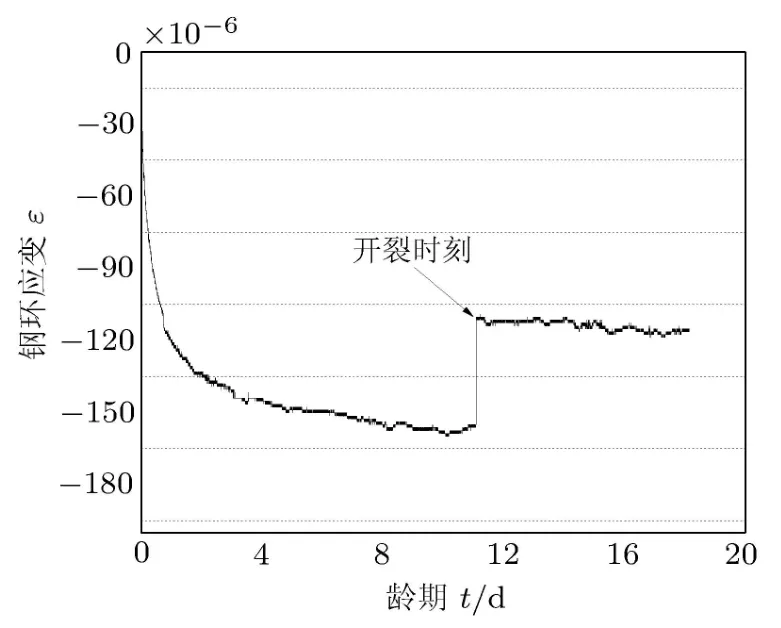
图2 钢环应变值回滞示意图

1 限制收缩环形试验的发展现状

Carlson[29]于1942年提出了用限制收缩圆环试验的方法研究水泥浆和砂浆的抗裂性能.1988年，Carlson等[30]采用限制收缩圆环试验研究不同混凝土配合比对抗裂性的影响.之后，限制收缩圆环试验广泛应用于混凝土收缩开裂问题的研究，但是在定量分析开裂机理方面并没有实质性的进展.Grzybowski等[31]提出基于混凝土损伤力学的破坏模型，采用一维收缩应变单元进行分析，将单元分为多层间隔小单元计算应变增量.其中，应变增量又分为非开裂区应变、开裂区应变以及表面纤维应变三部分，分析过程较为复杂.Shah等[32]提出了一种基于线弹性断裂力学的分析模型预测混凝土的开裂时间，并与实验观测相符合.在此基础之上，Weiss等[33]通过非线弹性断裂力学理论证明了约束混凝土的收缩开裂是与几何尺寸有关的，材料的脆性越小，几何尺寸的影响越大.Shah等[32]提出的断裂分析模型在分析收缩开裂问题时并没有提供关于拉伸应力和徐变的定量分析，See等[10]发现限制收缩开裂不仅与抗拉强度有关，还与收缩率和拉伸徐变有关，限制收缩圆环试验可以用来量化限制收缩条件下混凝土的拉伸徐变特性.拉伸徐变可以起到释放应力、延长开裂时间的作用，减缩剂通过减小收缩率和潜在开裂可能来增强混凝土的抗裂性.2004年之前，AASHTO建议应用标准圆环试验提供不同配合比混凝土的抗裂能力定性信息，但并没有详细说明试件的破坏机理.Hossain等[34]通过对限制收缩混凝土圆环试件的残余应力发展、应力松弛以及圆环试验的结果和材料性能的分析，详细说明了怎样用圆环试验分析混凝土开裂的应力发展.并提出了限制度ψ和实际外圆周的最大拉应力σActual−Max的算式.这为选择不同尺寸试件形式来模拟实际工况的约束度试验设计提供了参考.

虽然限制收缩圆环试验已经被广泛应用于早龄期混凝土开裂问题的研究，不同的研究人员采用相似的试验形式，但是养护条件、几何尺寸、边界条件会有所不同.Hossian等[5]通过限制收缩圆环试验研究试件的几何尺寸和边界条件对开裂的影响，进行了自由收缩试验，限制收缩圆环试验和声波频谱法试验，对混凝土的开裂时间、开裂位置及其开裂传播方向进行分析.Abbasnia等[35]通过试验与数值模拟相结合，引入与材料特性和湿度条件相关的收缩系数来预测干燥收缩产生的应变.Moon等[36]考虑到径向湿度梯度的影响，提出外圆周表面干燥的限制收缩厚环混凝土试件的残余应力分析方法，进行应力场的叠加：一部分来自湿度梯度，另一部分来自内部钢环的约束.减缩剂和聚乙烯醇纤维分别对限制收缩圆环试验的影响已经研究过，但是关于两者混合后的影响并没有进行研究分析，Passuello等[37]对减缩剂和聚乙烯醇纤维混合对混凝土开裂特性进行试验研究表明：减缩剂可以延迟裂缝出现的时间，减少裂缝宽度的40%，纤维的加入不能改变开裂时间，但是确实可以降低裂缝的宽度，粗纤维可以降低70%左右，微纤维可以降低几乎90%.

以上主要是对素混凝土限制收缩环形试验的介绍，该试验方法在其他种类的混凝土中也得到了较广泛的应用.大部分关于自密实混凝土的研究主要是比较自密实混凝土与普通混凝土的体积变化，而Turcry等[11]通过限制收缩圆环试验研究自密实混凝土的开裂趋势，通过研究材料特性：收缩、弹性模量、徐变与断裂性能去分析自密实混凝土的抗裂性，并且与普通混凝土进行比较.Nguyen等[15]通过限制收缩圆环试验对早龄期高性能混凝土(high performance concrete,HPC)的开裂研究表明：钢环厚度越大，开裂时间越早，混凝土壁厚越大，开裂时间越晚，水灰比越大，开裂时间越晚.Li等[20]对超高性能混凝土中加入了钢渣掺合料来研究收缩裂缝，通过平板试验和限制收缩圆环试验进行分析，结果表明矿物掺合料可以推迟开裂，钢渣混凝土可以提高耐久性.Yoo等[23]发现与普通混凝土相比超高性能纤维增强混凝土具有较强的材料性能，通过圆环试验对超高性能纤维增强混凝土限制收缩应力研究表明：通过钢环应变与温度以及钢环应变与贯入阻力的比较得到：当贯入阻力为1.5MPa时，限制收缩应力开始发展，同时也作为自收缩的零点.高英力等[28]对粉煤灰高强轻骨料混凝土的早期自收缩和抗裂性进行了研究，研究表明掺入粉煤灰可以显著改善混凝土早期的抗裂性.虽然限制收缩圆环被较为广泛地应用于混凝土在限制收缩条件下的抗裂性评估，不过圆环法试验也存在着一些缺点，如：对于高抗裂性混凝土圆环试件提供约束不足，在试验周期内混凝土开裂时间较长或不开裂，无法有效评估其早龄期的抗裂性，一些学者提出了椭圆环的形式进行试验.董伟等通过圆环试验的方法证实了很多学者提出的薄环假设以及开裂时间和位置[38]，同时，还提出了运用椭圆环法去分析混凝土的开裂趋势，通过数值模拟分析与所得试验结果进行比较[39]，并以基于虚拟裂纹粘聚力的裂纹扩展准则来评测裂缝的起裂、稳定扩展及失稳扩展的全过程[4041].以上的科研成果不断推动着混凝土限制收缩的研究.

2 限制收缩环形试验分析方法

2.1 最大拉应力理论

早龄期混凝土在内部钢环的约束作用下会产生环向拉应力，徐变会释放部分应力，控制混凝土破坏的为内部残余应力(考虑徐变)，当混凝土的残余应力超过混凝土的抗拉强度时，混凝土会开裂.Hossain等[34]和Moon等[36]采用混凝土残余应力与劈裂抗拉强度相比较来判断混凝土的开裂.

限制收缩混凝土圆环残余应力的计算主要分为两种情况：径向收缩均匀与径向收缩不均匀.试验过程中，混凝土薄环(壁厚37.5mm)存在湿度梯度，但由于厚度小，可以忽略湿度梯度的影响，沿径向近似为均匀收缩.混凝土厚环(壁厚75mm)采用上下表面干燥方式时，径向不存在湿度梯度，近似为径向均匀收缩[34].基于此,Hossain等[34]提出最大残余应力σActual−Max的计算公式

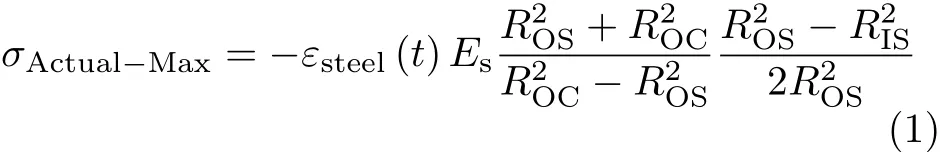
式中，ROS为钢环外径，RIS为钢环内径，ROC为混凝土环的外径，ES为钢环的弹性模量，εsteel(t)为试验测得的时刻钢环应变值.

对于75mm壁厚外圆周表面干燥的混凝土环，径向存在湿度梯度导致不均匀收缩，应力场由内部钢环约束与不均匀收缩产生的应力进行叠加得到.基于此方法，Moon等[36]提出了残余应力计算公式

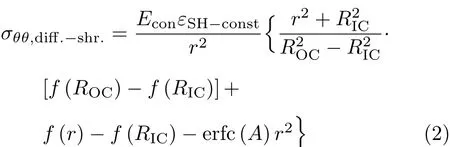
式中,σθθ,diff.−shr.为不均匀收缩下混凝土内部环向残余应力，Econ为混凝土的有效弹性模量，εSH−const为自由收缩常系数，r为柱坐标系下径向距离，RIC为混凝土环内径，erfc(A)为误差修正表达式.

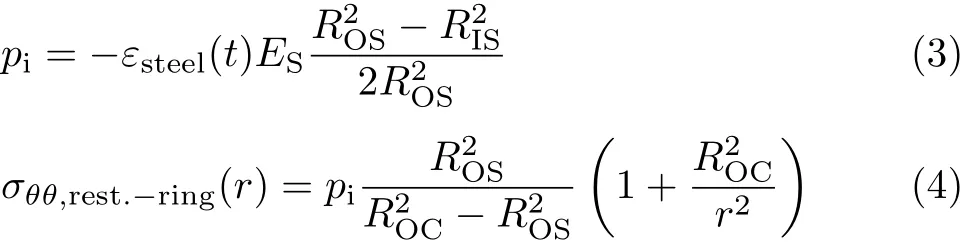
式中，pi为虚拟外部压应力，ES为钢环弹性模量，σθθ,rest.−shr.(r)为由约束钢环产生的环向应力.将式(2)和式(4)叠加就可以得到混凝土内部的残余应力.具体计算过程参见文献[36].

在求得残余应力后，Hossain等[34]引入潜在开裂的概念ΘCR，用来预测开裂可能性.对于潜在开裂的定义是

其中，C以及fspa这两个回归系数是通过不同的水灰比确定的.当潜在开裂ΘCR的数值接近1时，试件会出现裂缝.不过它也存在着自己的局限性，即没有考虑到几何尺寸的影响.

2.2 断裂力学理论

有学者提出由于混凝土的抗拉强度存在尺寸效应，混凝土在限制收缩状态下呈现拉压复合应力状态，此时采用混凝土单轴抗拉强度来进行判断是不准确的[1132].基于此，Ouyang等[42]采用断裂力学的R阻力曲线方法，通过裂纹抵抗阻力曲线(R曲线)与裂纹驱动力曲线(G曲线)相比较来分析混凝土的开裂，并明确了试验中钢环应变产生滞回的时刻对应试件的失稳破坏状态.

该判断方法的核心问题是求得结构的裂纹驱动力曲线(G曲线)和裂纹扩展阻力曲线(R曲线)[42].混凝土的破坏过程可看做3部分：起裂阶段，稳定扩展阶段，失稳扩展阶段.研究表明[32,42]，混凝土进入失稳扩展阶段时，可以观测到裂缝出现，此时G和R满足以下两个条件，即G=R和∂G/∂a=∂R/∂a.如图3所示，图中的A点此时就满足前面的两个条件，即混凝土进入失稳扩展阶段，出现裂缝.

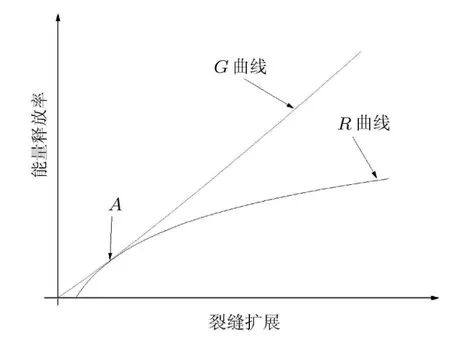
图3 G和R曲线图

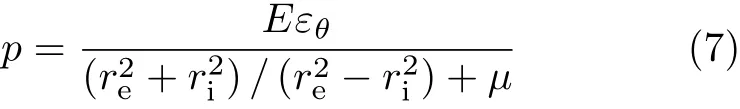
其中，re，ri分别表示混凝土圆环试件的外径和内径，εθ表示试验测得的应变值，E为弹性模量.

求得压力p后，运用数值方法来计算应力强度因子KI

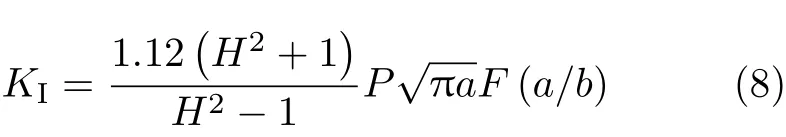
Ouyang等[42]运用无限大板的方法通过3个板试件对裂纹扩展阻力曲线(R曲线)进行了推导，得到R曲线的表达式

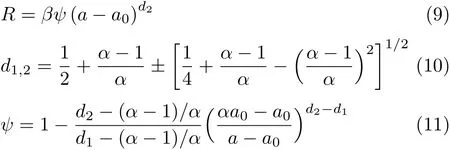
式中，α和β分别为与材料断裂参数相关的常数;ac为临界裂纹长度;a0为初始裂缝长度;d,ψ分别表示裂缝长度的函数.

研究表明[43]，至少需要两个断裂参数去描述半脆性材料的断裂韧度，即临界应力强度因子和临界裂纹尖端张口位移CTODC.这两个断裂参数可以通过文献[44]推荐的预制缝高比为1/3的三点弯曲梁试验来获得，然后通过下面的表达式分析反推可以得到关于α的计算表达式

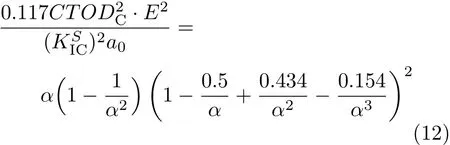
另一参数β可由下式求得

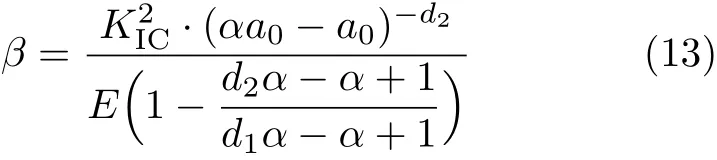
具体推导过程可以参考文献[32].圆环试件的裂纹扩展阻力曲线(R曲线)通过试验与数值计算求出后与裂纹驱动力曲线(G曲线)结合可确定混凝土的极限应变值点，该点满足G=R和∂G/∂a=∂R/∂a两个条件.满足这两个条件的点就是混凝土的最大容许应变点，当混凝土的应变，即自由收缩与徐变的差值大于混凝土的极限容许应变时，混凝土发生破坏.

3 限制收缩环形试验的影响因素

除了材料自身特性外，内部钢环与外部混凝土圆环的厚度、干燥方式及预制裂缝也是影响试验结果的重要因素.如：不同的钢环厚度会影响约束度的强弱.混凝土环厚度变化最重要的是引起湿度梯度的变化，一定程度上改变试验的破坏机理，使裂缝出现位置及扩展方向发生变化.干燥方式主要影响混凝土截面的湿度分布，进而影响到应力计算以及开裂位置.下面就以上各因素的影响做详细分析.

3.1 试件几何尺寸的影响

试件几何尺寸主要集中表现在混凝土圆环的厚度和内部约束钢环的厚度两方面.实际工程中混凝土的骨料粒径通常为5～25mm.为了满足三倍骨料粒径的要求，在不同骨料粒径混凝土的抗裂性评测中，需要调整混凝土圆环的厚度.研究外界约束条件的强弱时，需要采用不同的钢环厚度.

研究表明[45]，混凝土厚度的变化会引起破坏机理的改变.当混凝土环较薄时，湿度沿厚度方向变化不大，可近似认为湿度沿整个截面是均匀分布的.进而采用混凝土内环施加均匀内压力的方式来模拟收缩效果，拉应力沿厚度方向均匀分布，此时，裂缝将形成于混凝土内环(收缩受到钢环约束所引起).随着龄期增长以及水分的散失，裂缝逐渐向外环扩展直到贯穿整个截面.随着混凝土厚度的增加，湿度梯度将逐渐增强，内部钢环提供的约束作用相对减弱，沿厚度方向应力分布不同[46]，导致裂缝形成于外环，并逐渐向内环扩展[34,36].根据Weiss[45]的试验观测，75mm壁厚的混凝土在限制收缩作用下裂缝产生于外侧并向内侧扩展，37.5mm壁厚的混凝土在限制收缩作用下裂缝产生于内侧并向外侧发展，很好地说明了混凝土厚度对于试验的影响.

在评定内部钢环约束作用的强弱时，See等[10]提出了约束度的概念，使得圆环试件的开裂发生在合理的时间域内.之后，Moon等[47]对约束度ψ进行研究，可以选择合理的试件尺寸最大程度地模拟实际工况.在考虑均匀收缩的条件下，对于约束度ψ的定义为

式中，ΔLfree为混凝土自由收缩的位移，ΔLrestrain为约束条件下混凝土的位移.

在限制收缩圆环试验的条件下，USH/RIC(t)为混凝土环内表面t时刻的自由收缩位移，US/ROS(t)为钢环约束下混凝土环内表面t时刻的实际位移，约束度定义为

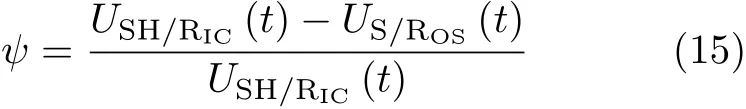
其大小在0到1之间.0代表钢环与混凝土环之间无约束，1代表完全约束.根据Weiss的研究[44]，均匀收缩(不考虑湿度梯度)情况下，自由收缩位移可以根据混凝土线性应变求得，约束混凝土圆环的真实位移可以根据测得的钢环内表面的应变求得.根据求得的位移可以得到约束度的进一步的算式

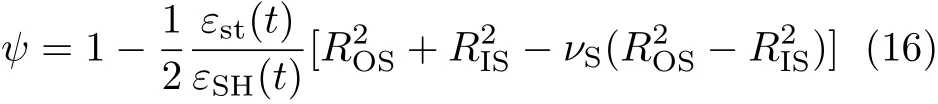
式中，ROS表示钢环外表面的半径，RIS表示钢环内表面的半径.其中影响最大的钢环应变与混凝土线性应变的比值(εst(t)/εSH(t))是由试件的尺寸、钢环和混凝土圆环的材料特性与尺寸决定的.这说明了提供不同的混凝土和约束钢环，便决定了试验过程中不同的约束程度，在试验中得到了体现.Hossain等[34]通过理论分析发现比值εst(t)/εSH(t)与混凝土圆环和钢环接触面产生的压力有直接关系，因此引入压力p0的理论计算.进而得到约束度的最终表达式

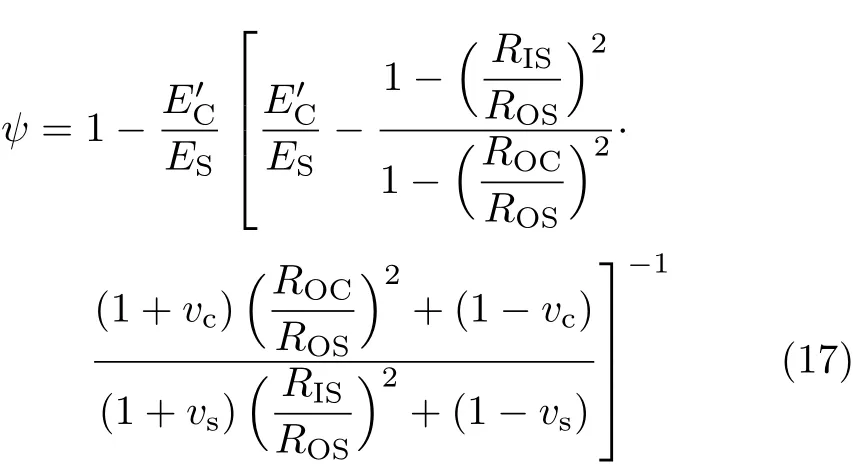
从公式可以看出,约束度与混凝土环和钢环的尺寸以及材料属性有关.研究人员可以根据约束度选择合适的试件尺寸进行试验，更好地符合实际工况.之后，Moon等[47]通过有限元分析发现，不同的干燥方式对于约束度的影响很小，因此约束度的表达式在均匀收缩和非均匀收缩的条件下都是适用的.

3.2 边界条件的影响

边界条件主要是指干燥方式以及水分散失面面积与体积的比值(s/v)两个方面.限制收缩试验中，干燥方式主要分为上下表面干燥，外圆周表面干燥两种.两种干燥方式主要影响着混凝土截面的湿度分布.对于37.5mm混凝土壁厚的薄环和75mm混凝土壁厚的厚环，不同的干燥方式下混凝土开裂时间、圆环的裂缝位置是有区别的，主要是由于不同的干燥方式使得混凝土水分散失方式改变，进而导致湿度梯度变化，影响到混凝土内部的应力分布. Carlson[48]与Băzant等[49]对湿度梯度进行了研究，提出运用非线性形式的菲克第二定律去表示混凝土的水分散失.不过，Moon等[36]在研究过程中使用了线性扩散方程进行计算，提出一个简单湿度梯度的表达式

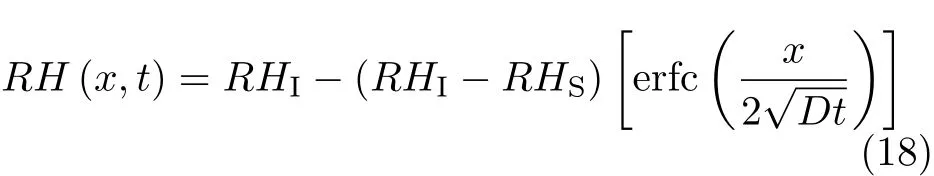
其中，RHI表示混凝土内侧的湿度，RHS表示混凝土外侧的湿度，erfc表示误差修正的表达式，D为与时间相关的湿度扩散系数.图4为应用式(18)计算的湿度梯度分布图.

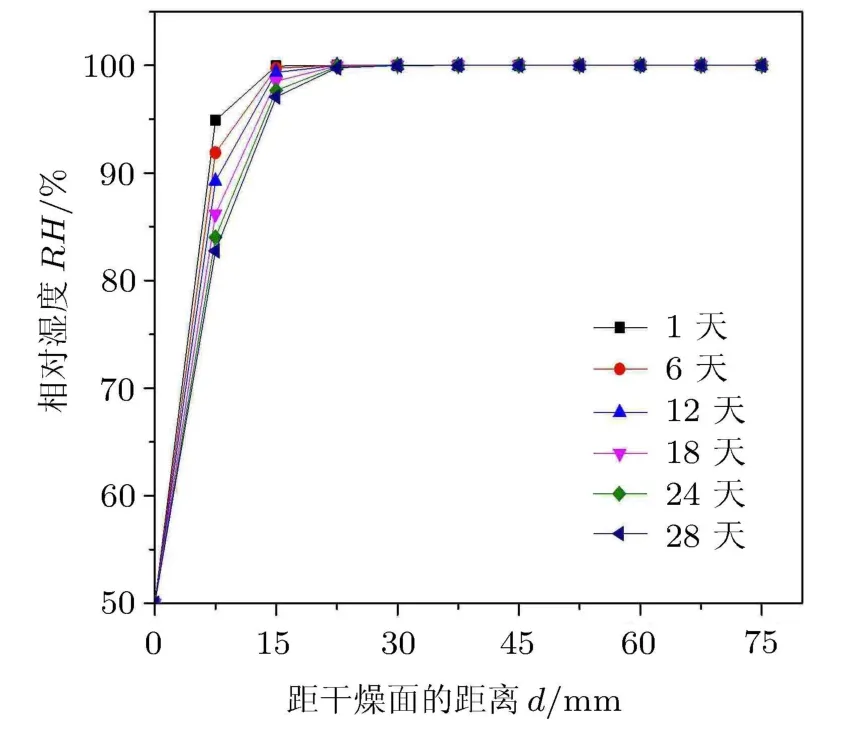
图4 相对湿度梯度计算

Hossian等[5]对边界条件的影响进行了研究，试验中设定两种干燥方式：上下表面干燥，外圆周表面干燥.试件从上下表面干燥时，沿径向不存在湿度梯度，但沿高度方向存在湿度梯度；试件从外圆周表面干燥时，沿径向会存在湿度梯度，径向收缩为不均匀收缩.

研究不同混凝土环厚度对内表面压力的影响时，外圆周表面干燥的圆环试件内表面压力要比上下表面干燥圆环试件内表面压力低.这种结果是不同的体表比(s/v)造成的，体表比(s/v)越大，内表面压力越大，试件开裂越早.而上下表面干燥的试件体表比要大于外圆周表面干燥的试件.在Hossain等[5]的试验中，混凝土壁厚为37.5mm的两种干燥方式的内表面压力基本一样，这正是由于它们的体积比(s/v)是基本一样.所以，在边界条件的影响中，体积比(s/v)也是一个比较重要的因素.

3.3 预制裂缝的影响

为了提高试验效率，减少开裂时间，诱导开裂的位置，在混凝土内部预制裂缝被部分学者应用于限制收缩试验中.Shah等[50]通过限制收缩圆环试件上预制裂缝进行试验研究，结果表明[46]，混凝土在限制收缩条件下具有在混凝土壁外侧或者内侧开裂的可能，因此预制裂缝的位置也应该进行区分. Shah通过限制收缩圆环试验对上部预制裂缝与未预制裂缝的两种混凝土试件进行比较分析，采用声波频谱法对圆环试验进行了分析.Shah将这些特性分成了三个时间段区域.在第一段时间区域内，两种混凝土圆环试件应力都在缓缓地升高，直到到达一个峰值，此时即将进入第二段时间区域.在此时间段区域内，应力趋势比较平稳，但是在很短暂的时间内应力会出现不稳定的波动，并且呈现出缓慢下降的趋势，这是由于微裂缝扩展并贯通释放应力从而使得应力水平下降，同时还可以发现未预制裂缝的试件的应力要高于预制裂缝的试件的应力.在第三个时间段区域内，未预制裂缝的试件的应力缓慢地下降，这与裂缝稳定扩展的理论是相契合的.郑建岚等[51]、周小菲[52]、Soroushian等[53]采用诱导开裂法，在限制收缩板式试验中增设隔板以及加设三角形钢条，确定开裂位置，加速开裂时间.从试验的角度来分析，预制裂缝的方法确实缩短了试件的开裂时间，也很方便地预测裂缝出现的位置.但在实际应用中，混凝土的开裂过程通常是从无裂缝到出现裂缝然后再到裂缝的不稳定扩展，人为的在混凝土上预制裂缝，容易使材料产生缺陷从而出现应力集中，这样会让混凝土跳过裂缝由“无”到“有”的过程，使得限制收缩的破坏机理发生不同程度的改变.

此外，在环形试验破坏机理的分析中，断裂力学是目前研究学者普遍采用的方法.而在断裂分析中，预制裂缝的存在是应用断裂理论的基本前提.但对比标准的试验方法的试件，是没有预制裂缝的，这就造成理论与实际试验的不相符.Ouyang等[42]、Băzant等[54]的研究表明，考虑混凝土不均质性及缺陷的影响，2mm的预制裂缝对试件最后的破坏分析结果不会产生影响.在Zhou等[39]的研究中，通过在2mm预制裂缝上施加粘聚力，进一步减小了预设缺陷对于分析结果的影响.在满足应用断裂理论的基本前提下，实现了限制收缩条件下环形试验破坏机理的分析.

4 材料性能对限制收缩环形试验的影响

4.1 收缩徐变的影响

混凝土的徐变是指在持续载荷作用下，混凝土结构变形将随时间增长而不断增加的现象.在加载初期发展较快，随后逐渐减弱，延续时间很长.Altoubat等[55]认为应力松弛机制会抵消部分应力，而应力松弛恰恰也是应力随着时间的增长而减小，这是一种广义上的蠕变.预测限制收缩混凝土环开裂性能时，收缩徐变也会由于应力松弛而使圆环应力减小.

收缩徐变在早龄期混凝土的应力发展上有重要的影响，混凝土收缩会使约束圆环产生压应力，收缩徐变通过应力松弛机制抵消部分的收缩，从而达到延缓开裂时间的效果.虽然已经认识到混凝土收缩徐变的重要性，但是关于早龄期收缩徐变的研究还十分有限[55].

在收缩徐变的应力分析中，Kovler[56]提出了随时间调整的等效模量的方法，需要将弹性应变与收缩徐变一起考虑.恒定温度场中，单轴压力下的混凝土变形的各个组成部分是：瞬时应变(εel)、徐变(εcr)和自由收缩应变(εfs).其中，瞬时应变起到很小的作用.公式表示如下

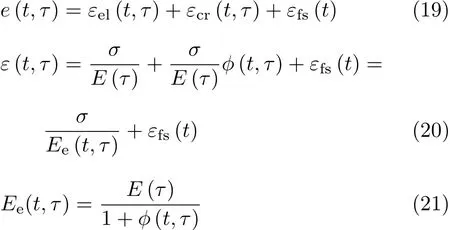
式中，τ为施加载荷时间，E(τ)为混凝土在τ时的弹性模量，φ(t,τ)为徐变系数(徐变与瞬时应变的比值).通过公式看出，要求得最后的等效模量Ee(t,τ)，就要求出徐变系数，然后可以通过试验求出等效模量.

See等[10]对圆环试件的收缩裂缝特性进行研究时发现，限制收缩条件下的混凝土的拉伸徐变要低于常应力下的拉伸徐变，因此将常载荷试验方法得到的拉伸徐变特性用于限制收缩混凝土单元上,将会高估试验材料的抗裂性.

欧洲混凝土规范CEB-FIP mode code 2010建议对混凝土限制收缩的应变采用弹性应变和徐变求和的方法来计算总应变，并给出了计算公式

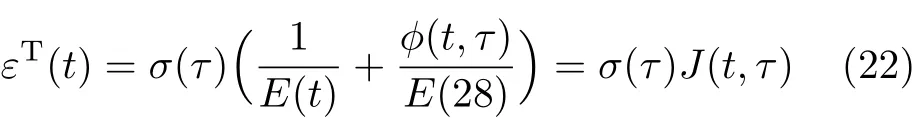
其中，t为徐变分析的时间，τ为应力σ(τ)施加的时间，E(τ)和E(28)分别表示τ天和28天时的弹性模量，φ(t,τ)为徐变系数，J(t,τ)为单位应力下的依赖应力的总应变，它可以很好地反映混凝土的总应变与内部应力的关系.求最后的总应变εT(t)时，采用上述公式对时间积分即可.

4.2 混凝土力学性能的影响

实际工程中混凝土所处的约束条件是不同的，为了评估不同约束条件下混凝土的抗裂性，需要设计与其约束度相匹配的限制收缩试验，在设计试验时需要根据不同特性的混凝土(主要是不同的弹性模量)，选择合理的钢环与混凝土环的厚度.See等[10]通过对标准限制收缩环形试验的研究，发现AASHTO和ASTM规范给出的标准试验尺寸对于普通强度的混凝土所提供的约束度大致为60%和75%.为了提供合适的试验几何尺寸，Moon等[47]提出了限制收缩圆环试验约束度的概念并且理论推导出约束度的计算表达式.提出了约束度除了受到钢环与混凝土环壁厚的影响之外，混凝土的弹性模量也是主要影响因素之一.在其他条件不变的情况下，混凝土的弹性模量越大其约束度反而会下降.董伟等[57]针对限制收缩椭圆环约束度进行理论研究，得到了限制收缩椭圆环的约束度计算表达式，得到了与Moon相同的结论.但由于试件几何形式的不同，椭圆环约束度中弹性模量的影响较圆环更小.此外，圆环试验中，增加钢环壁厚可显著提高约束度，而椭圆环约束度主要由钢环的长短轴比例决定，钢环壁厚影响较小.

5 限制收缩椭圆环试验方法的应用

研究表明，由于圆环试验存在约束度较低的问题，使得试验中出现第一条裂缝需要较长的时间[58].圆环试验的约束度主要是由内部钢环所提供，当钢环厚度不足时,钢环无法提供足够的约束度会导致圆环试件不会出现裂缝[10,36].同时由于圆环的几何特征的影响，沿圆环周向出现裂缝是等可能性的，给试验观测带来不方便，也不能准确预测出裂缝出现的位置.为了解决上述问题，加速开裂时间,缩短试验周期，He等[59]在研究水泥基材料时采用了一种新颖的椭圆环试验，证实了椭圆环试验可以促进开裂，缩短开裂时间.同时，椭圆环试件中裂缝出现的位置是可以近似确定的，减少了采集裂缝产生和扩展的实验设备和资源的投入.椭圆环试件可以加速开裂,主要是由于几何形式引起的应力集中，周向应力由于椭圆钢环提供的约束度不同而大小不同.内部钢环的形状对约束度有比较大的影响，在椭圆环试件中长短轴比例的影响尤其明显.Zhou等[60]研究发现，对于薄壁混凝土(37.5mm)试件，长短轴比值为2的椭圆环可显著加速开裂时间.Dong等[61]提出了一种基于断裂力学的数值方法分析混凝土的裂缝扩展过程，假设一个虚拟温度场施加于混凝土试件，其引起的收缩与干燥收缩是等效的，通过有限元分析出椭圆外环干燥时的应力强度因子，根据实验结果也验证了长短轴比为2的薄壁椭圆环试件比圆环试件能提供更好的约束效果.

Dong等[62]结合虚拟裂缝模型研究了不同壁厚的椭圆环试件的开裂机理.结果表明，薄壁椭圆环试件开裂区位于与钢环接触一侧并向外扩展，内部钢环起到主要的限制作用，厚壁椭圆环试件则产生于混凝土试件外侧并向内侧扩展，不均匀的湿度分布起到关键作用.薄壁椭圆环的开裂原因主要来自内部钢环的限制作用，但厚环的开裂主要由混凝土自身不均匀收缩造成.因此，Dong等建议对于薄壁椭圆环试件，采用外环干燥的方式是合理的，对于厚壁椭圆环试件，外环干燥的方式削弱了内部钢环的约束作用，因此上下面干燥的方式更加合理.

之前对于圆环试验已经研究过约束度的理论推导与计算，为圆环试验的实验室设计提供了参考.对于椭圆环试验，董伟等[57]在综合考虑试件几何、混凝土厚度、钢环厚度以及混凝土弹性模量之后，通过计算椭圆环试件在自由收缩和限制收缩下的位移，最后得出了椭圆环试验约束度的表达式，并且针对高约束度下的早龄期混凝土，进行了椭圆环的试验设计.

6 存在的问题及发展趋势

对于早龄期混凝土限制收缩开裂问题，大部分研究人员选择限制收缩环形试验进行研究，并且经过国内外很多学者从不同角度进行的试验与数值模拟分析，已经形成了一定的研究体系和理论架构.在限制收缩圆环试验中，提出的约束度的计算方法就是一个很经典的理论解释，在试验与数值推导过程中，采用的是线性扩散系数的方法，但是由于混凝土的厚度不同,其内部的湿度梯度分布是不均匀的，这样做出的结论会有一定的误差.最初在ASTM和AASHTO建议的标准试验中，通过内部钢环应变数值的突然回滞来预测混凝土试件的开裂，但是并不能够说明具体裂缝的开裂位置，给试验观测带来一定的困难.

限制收缩环形试验中，内部钢环的约束对混凝土试件的影响很大，限制了混凝土试件的收缩，从而导致混凝土内部的拉应力不断增大，直到破坏.但是在研究内部钢环约束的时候，普遍采用将约束钢环的作用简化为沿混凝土试件内表面均匀分布的压力，主动给混凝土施加应力导致开裂，这样的破坏机理是与混凝土自身的收缩破坏有所不同的.虽然得到的试验结果与模拟分析的结果是合理的，但在机理上可能存在一定的问题.

此外，虽然限制收缩圆环被较为广泛地应用于混凝土在限制收缩条件下的抗裂性评估，不过圆环法试验中也存在着一些缺点，如：开裂位置不好预测，可能会存在混凝土开裂时间较长或不开裂的情况.一些学者提出了用椭圆环限制收缩进行试验的方法，以提供更高的约束度，并且可以缩短试验周期，更方便地监测裂缝的扩展[39].而且椭圆环试件还有一个特点，由于其自身长短轴的影响，椭圆环试件在长轴附近会发生应力集中现象,开裂多发生在长轴附近.不过椭圆环的内部钢环对椭圆环的约束作用是不均匀的，无法用应力解析式去评价约束作用的强弱.对椭圆钢环的等效应力的计算是需要以后继续研究和解决的问题.

1 Weiss J,Yang W,Shah SP.Factors in fl uencing durability and early-age cracking in high strength concrete structures.ACI Special Publication,2000,189:387-410

2 Shah SP,Weiss J,Yang W.Shrinkage cracking—Can it be prevented?Concrete International,1998,20(4):51-55

3 Kovler K.Testing system for determining the mechanical behavior of early age concrete under restrained and free uniaxial shrinkage.Materials and Structures,1994,27(6): 324-330

4 Shales CA,Hover KC.In fl uence of mix-proportion and construction operations on plastic shrinkage cracking in thin slabs.ACI Materials Journal,1998,85(6):495-504

5 Hossain AB,Weiss J.The role of specimen geometry and boundary conditions on stress development and cracking in the restrained ring test.Cement and Concrete Research, 2006,36(1):189-199

6侯景鹏,袁勇,柳献.混凝土早期收缩试验方法评价.混凝土与水泥制品,2003，(5):1-4

7 AASHTO PP34-1999.Standard practice for estimating the cracking tendency of concrete.AASHTO,1998

8 Astm C1581.Standard test method for determining age at cracking and induced tensile stress characteristics of mortar and concrete under restrained shrinkage.2004

9中国土木工程学会.CCES 01-2004混凝土结构耐久性设计与施工指南.北京:建筑工业出版社,2004

10 See HT,Attiogbe EK,Miltenberger MA.Shrinkage cracking characteristics of concrete using ring specimens.ACI Materials Journal,2003,100(3):239-245

11 Turcry P,Loukili A,Haidar K,et al.Cracking tendency of self-compacting concrete subjected to restrained shrinkage: experimental study and modeling.Journal of Materials in Civil Engineering,2006,18(1):46-54

12 Geiker MR,Brandl M,Thrane LN,et al.On the e ff ect of coarse aggregate fraction and shape on the rheological properties of self-compacting concrete.Cement,Concrete and Aggregates,2002,24(1):3-6

13 Rozi`ere E,Granger S,Turcry P,et al.In fl uence of paste volume on shrinkage cracking and fracture properties of self-compacting concrete.Cement and Concrete Composites,2007,29(8):626-636

14王国杰.自密实混凝土圆环约束收缩试验研究.工程力学,2014, 31(12):173-180

15 Nguyen Q,Jiang LH,Zhu Q.Assessment of early-age cracking of high-performance concrete in restrained ring specimens.Water Science and Engineering,2010,3(1):113-120

16 Wiegrink K,Marikunte S,Shah SP.Shrinkage cracking of high-strength concrete.ACI Materials Journal,1996, 93(5):409-415

17 Chen K,Hu H,Chen ZH,et al.Cracking tendency prediction of high-performance cementations materials.Advances in Condensed Matter Physics,2014,(1):1-12

18 Kim S,Park J,Yoo D,et al.Shrinkage behavior of ultra high performance concrete at the manufacturing stage. The 3rd International Symposium on Ultra-High Performance Concrete and Nanotechnology in Construction,Kassel,Germany,2012

19 Park JJ,Yoo DY,Kim SW,et al.Bene fi ts of using expansive and shrinkage-reducing agents in UHPC for volume stability.Magazine of Concrete Research,2014,66(14): 745-750

20 Li YF,Guo HX,Wang LL.Shrinkage cracking of high performance concrete mixed with steel slag admixture.Key Engineering Materials,2011,462:867-871

21 Grzybowski M,Saha SP.Shrinkage cracking of fi ber reinforced concrete.ACI Materials Journal,1990,87(2):138-148

22 Yoo DY,Park JJ,Kim SW,et al.Combined e ff ect of expansive and shrinkage-reducing admixtures on the properties of ultra high performance fi ber-reinforced concrete.Journal of Composite Materials,2013,48(16):1981-1991

23 Yoo DY,Park JJ,Kim SW,et al.Early age setting,shrinkage and tensile characteristics of ultra high performance fi ber reinforced concrete.Construction and Building Materials,2013,47:427-438

24 Yoo DY,Park JJ,Kim SW,et al.In fl uence of ring size on the restrained shrinkage behavior of ultra high performance fi ber reinforced concrete.Materials and Structures,2014, 47(7):1161-1174

25 Ji T,Zhang B,Chen Y,et al.Evaluation method of cracking resistance of lightweight aggregate concrete.Journal of Central South University,2014,21:1607-1615

26 Gu¨neyisi E,Geso˘glu M,Mohamadameen A,et al.Enhancement of shrinkage behavior of lightweight aggregate concretes by shrinkage reducing admixture and fi ber reinforcement.Construction and Building Materials,2014,54: 91-98

27 Zhuang YZ,Chen CY,Ji T.E ff ect of shale ceramsite type on the tensile creep of lightweight aggregate concrete.Construction and Building Materials,2013,46:13-18

28高英力，龙杰，刘赫等.粉煤灰高强轻骨料混凝土早期自收缩及抗裂性试验研究.硅酸盐通报，2013,32(6):1151-1156

29 Carlson RW.Cracking of concrete.Boston Society of Civil Engineers,1942,29(2):98-109

30 Carlson RW,Reading TJ.Model study of shrinkage cracking in concrete building walls.ACI Structural Journal, 1988,85(4):395-404

31 Grzybowski M,Shah SP.Model to predict cracking in fi bre reinforced concrete due to restrained shrinkage.Magazine of Concrete Research,1989,41(148):125-135

32 Shah SP,Ouyang C,Marikunte S,et al.A method to predict shrinkage cracking of concrete.ACI Materials Journal, 1998,95(4):339-346

33 WeissJ,YangW,ShahSP.In fl uenceofspecimen size/geometry on shrinkage cracking of rings.Journal of Engineering Mechanics,2000,126(1):93-101

34 Hossain AB,Weiss J.Assessing residual stress development and stress relaxation in restrained concrete ring specimens.Cement and Concrete Composites,2004,26(5):531-540

35 Abbasnia R,Shekarchi M,Ahmadi J.Evaluation of concrete drying shrinkage related to moisture loss.ACI Materials Journal,2013,110(3):269-277

36 Moon JH,Weiss J.Estimating residual stress in the restrained ring test under circumferential dying.Cement and Concrete Composites,2006,28(5):486-496

37 Passuello A,Moriconi G,Shah SP.Cracking behavior of concrete with shrinkage reducing admixtures and PVA fi bers.Cement and Concrete Composites,2009,31(10): 699-704

38 Dong W,Zhou XM,Wu ZM.In fl uence of specimen thicknesson cracking behaviorin restrained shrinkage ring test.International Journal of Engineering and Technology,2013,5(6):698-702

39 Zhou X,Dong W,Oladiran O.Experimental and numerical assessment of restrained shrinkage cracking of concrete using elliptical ring specimens.Journal of Materials in Civil Engineering,2013,26(11):04014087

40 Dong W,Wu ZM,Zhou XM.Calculating crack extension resistance of concrete based on a new crack propagation criterion.Construction and Building Materials,2013,38(1): 879-889

41 Dong W,Zhou XM,Wu ZM.On fracture process zone and crack extension resistance of concrete based on initial fracture toughness.Construction and Building Materials, 2013,49(12):352-363

42 Ouyang C,Shah SP.Geometry-dependent R-curve for quasi-brittle materials.Journal of the American Ceramic Society,1991,74(11):2831-2836

43 Băzant ZP,Kazemi MT.Determination of fracture energy, process zone length and brittleness number from size effect,with application to rock and concrete.International Journal of Fracture,1990,44(2):111-131

44 XuS,ReinhardtHW.Determinationofdoubledetermination of double-K criterion for crack propagation in quasi-brittle fracture.Part I:experimental investigation of crack propagation.International Journal of Fracture, 1999,98(2):111-149

45 Weiss J.Prediction of early-age shrinkage cracking in concrete elements.[PhD Thesis].Evanston:Northwestern University,1999

46 Abbasnia R,Shekarchi M,Ahmadi J.Evaluation of concrete drying shrinkage related to moisture loss.ACI Materials Journal,2013,110(3):269-277

47 Moon JH,Rajabipour F,Pease B,et al.Quantifying the in fl uence of specimen geometry on the results of the restrained ring test.Journal of ASTM international,2006, 3(8):1-14

48 Carlson RW.Drying shrinkage of large concrete members.ACI Journal Proceedings,1937,33(1):327-336

49 Băzant ZP,Najjar LJ.Drying of concrete as a nonlinear di ff usion problem.Cement and Concrete Research,1971, 1(5):461-473

50 Shah HR,Hossain AB,Mazzotta G,et al.Time-dependent fracture in restrained concrete:The in fl uence of notches and fi bers.Advances in Cement and Concrete IX:Volume Change,Cracking and Durability,Copper Mountain,Colorado,2003

51郑建岚,王雪芳,罗素蓉.一种有效测试早龄期混凝土开裂性能的试验方法.建筑材料学报，2009，12(2)：209-213

52周小菲.混凝土抗开裂性能的评价方法与影响因素研究.[硕士论文].北京：清华大学,2011

53 Soroushian P,Ravanbakhsh S.Control of plastic shrinkage cracking with specialty cellulose fi bers.ACI Materials Journal,1998,95(4):429-43554 Băzant ZP,Kim J,Pfei ff er PA.Nonlinear fracture properties from size e ff ect tests.Journal of Structural Engineering,ASCE,1986,112(2):289-307

55 Altoubat SA,Lange DA.Creep,shrinkage,and cracking of restrained concrete at early age.ACI Materials Journal, 2001,98(4):323-331

56 Kovler K.Drying creep of concrete in terms of the ageadjusted e ff ective modulus method.Magazine of Concrete Research,1997,49(181):345-351

57董伟，罗昊，王福禄等.限制收缩椭圆环约束度理论研究与试验设计.建筑材料学报，2016,http://www.cnki.net/kcms/detail/31.1764.TU.20160523.1641.042.html

58 Bentur A,Kovler K.Evaluation of early age cracking characteristics in cementitious systems.Materials and Structures,2003,36(3):183-190

59 He Z,Zhou X,Li Z.New experimental method for studying early-age cracking of cement-based materials.Materials Journal,2004,101(1):50-56

60 Zhou X,Oladiran OG,Dong W.On utilization of elliptical rings in assessing cracking tendency of concrete.4th International Conference on the Durability of Concrete Structures,West Lafayette,USA,2014

61 Dong W,Zhou X,Wu Z.Investigation of the initiation and propagation of shrinkage cracking in a restrained elliptical ring test.Concreep 10,2015,http://dx.doi.orbg/10.1061/9 780784479346.085

62 Dong W,Zhou X,Wu Z,et al.E ff ects of specimen size on assessment of shrinkage cracking of concrete via elliptical rings:Thin vs.thick.Computers&Structures,2016,174: 66-78

(责任编辑:周冬冬)

OVERVIEW OF RING TEST TO ASSESS CRACKING RESISTANCE OF EARLY-AGE CONCRETE1)

WANG FuluDONG Wei2)YUAN Wenyan
(State Key Laboratory of Coastal and O ff shore Engineering,Dalian University of Technology,Dalian 116024,Liaoning,China)

The early-age concrete under the condition of restrained shrinkage is easy to crack,which would a ff ect safety and durability of the structure,as well as the applicability.So it is very important to provide a simple and e ff ective method to assess the crack resistance of the early-age concrete.In view of providing certain rigidity and the convenience of laboratory constraints,the restrained shrinkage ring test is widely used to evaluate the crack resistance of the concrete under restrained shrinkage conditions.This paper discusses the development of the restrained shrinkage ring test,the failure mechanism and the impact of three factors.The restrained shrinkage ring test is recommended as a standard test method by the American Association of State Highway and Transportation Officials(AASHTO)and the American Society for Testing and Materials(ASTM), and the test is conducted for di ff erent purposes,including the failure mechanism based on the maximum tensile stress fracture mechanics theory and the fracture energy to predict the concrete cracking.The annular test specimen geometry,the boundary conditions,the performance of the concrete materials and the pre-crack are considered as in fl uencing factors.A test method of elliptical ring is adopted,which can e ff ectively assess the crack resistance of the concrete under conditions of high degree of restraint.

early-age concrete,restrained shrinkage,failure mechanism,in fl uencing factors

TU528.1

A

10.6052/1000-0879-16-352

2016–10–25收到第1稿，2016–12–26收到修改稿.

1)国家自然科学基金(51478083)和中央高校基本科研业务费(DUT14LK06)资助.

王福禄,董伟,袁文岩.早龄期混凝土抗裂性环形试验研究进展.力学与实践,2017,39(2):120-129,151 Wang Fulu,Dong Wei,Yuan Wenyan.Overview of ring test to assess cracking resistance of early-age concrete.Mechanics in Engineering,2017,39(2):120-129,151