典型纳尺度结构的热振动1)

刘汝盟 王立峰

(南京航空航天大学机械结构力学及控制国家重点实验室，南京210016)

典型纳尺度结构的热振动1)

刘汝盟 王立峰2)Email:walfe@nuaa.edu.cn

(南京航空航天大学机械结构力学及控制国家重点实验室，南京210016)

王立峰，1977年生，南京航空航天大学机械结构力学及控制国家重点实验室教授,博士生导师.主要从事纳尺度系统动力学研究.2009年获全国优秀博士学位论文奖，2011年入选教育部“新世纪优秀人才计划”，作为第五完成人获得2012年国家自然科学奖二等奖，2013年入选江苏省333人才工程中青年学术带头人，2015年获得国家自然科学基金优秀青年科学基金项目资助并入选2015年度长江学者奖励计划青年学者项目，2016年入选江苏省333人才工程中青年科技领军人才.担任《力学与实践》期刊编委、中国力学学会微纳米力学工作组委员、青年工作委员会委员.

热振动是一定温度下纳尺度结构的固有运动，对其动力学行为有着重要的影响.当空间进入纳米尺度，结构呈现离散性，量子效应、边界效应、范德华力等变得不可忽略，纳尺度结构在热噪声随机激励下的动力学行为表现出众多异乎寻常的特性.以碳纳米管和石墨烯为代表的纳尺度碳材料具有优良的力学、电学和化学性质.在此介绍多种针对纳尺度结构热振动问题的研究方法、及碳纳米管和石墨烯的低温热振动、碳纳米管的非线性热振动研究进展.

石墨烯，碳纳米管，热振动，量子效应，非线性振动

引言

动力学行为是纳尺度结构不可忽略的组成部分，纳尺度结构的运动形式甚至比结构自身的形貌更为重要，引起这种运动的原因有电场或磁场激励、热涨落等.随着所研究的空间进入纳米尺度，相应的时间进入飞秒量级，能量尺度进入电子伏特量级，许多材料的物理、化学和力学性质随尺寸的减小而发生显著变化.同时由于多种不同于经典连续体的复杂特性，如结构自身的离散性、超高比表面积导致的表面效应、量子效应、范德华力作用等，导致纳尺度结构的动力学行为表现出很多异乎寻常的特征，同时也带来很多亟待解决的动力学问题.

一切物体的原子均在做不停的随机运动，其振动幅值与温度相关.电子系统中普遍存在的Johnson--Nyquist噪声[12]是热振动的典型例子.而对热振动更早的探索源自爱因斯坦对粒子布朗运动的开创性研究和Langevin方程的建立.人们研究了噪声对非线性随机系统动力学特征的影响，朱位秋等[34]建立了非线性随机系统动力学的哈密顿体系理论框架，为解决随机激励下非线性系统的动力学问题提供了一条新的路径.热振动的影响在微尺度下就开始表现出来，例如热噪声对微机电系统的分辨率和稳定性等性能起着至关重要的作用.在纳尺度下，由于热的作用，结构自身存在不可消除的固有振动，并且会引起系统状态参数的随机涨落[5].与宏观结构不同，纳尺度下热振动所对应的结构整体振幅不再是一个微小量.热引起的纳尺度结构动力学问题是自然存在、不可避免的[6].

随着加工技术和化学合成技术的进步，越来越多的纳尺度结构被发现和制造出来.纳机电系统由于尺寸极小，便于集成更多的功能，有着广阔的应用前景.随着精度要求的不断提高，分子热运动带来的纳机电系统的热振动问题尤其突出.尤其是当考虑热的影响之后，从动力学的角度来看，纳尺度温度效应可视为随机激励，如何建立准确描述随机激励下纳尺度结构动力学行为的力学模型，成为一项巨大的挑战.热振动问题已成为限制纳机械传感器灵敏度及纳机电系统性能的瓶颈问题.除此之外，热振动也有多种可供利用的方面，例如测量纳米线的热振动谱，可快速、无损的标定纳米线的弹性模量等力学参数；实现可控的分子尺度的能量传导是实现分子技术的根本，热振动与电子、声子、光子传播机制紧密相关，理解热振动问题有助于从本质上揭示材料的热传导问题.

如图1所示的碳纳米管和石墨烯等典型碳纳米结构，在电学、化学等方面也展现出多种优异特性[7].碳纳米结构可被应用于材料增强、能源存储器、纳米温度计等；在多种纳机电系统，如振荡器、时钟、传感器、场发射器中，碳纳米结构具有重要的潜在应用，而且碳纳米管更有可能应用于下一代原子力显微镜探针结构.

1 纳尺度动力学研究方法

1.1 实验方法

在纳尺度实验中，由于所要观测的对象尺寸非常小，而时间过程非常短，因此对实验设备的要求非常高.电子显微镜的发明突破了光学显微镜的极限，为纳米科技的发展提供了最重要的直接观测工具.20世纪60年代，电子显微镜技术逐步应用到材料研究中，使得在纳米尺度上观察材料结构特征成为可能.Binning和Rohrer于1982年利用扫描隧道显微镜获得第一张单原子台阶像，并于1983年获得第一张表面重构像.借助扫描隧道显微镜，不仅可以获得原子级别的空间分辨力，更能在纳尺度上操纵原子.1986年，斯坦福大学的Binning，Quate和Gerber发明了第一台原子力显微镜.原子力显微镜利用测量微悬臂梁位移，得到悬臂上探针与测试样品原子之间的作用力，从而达到测量的目的.原子力显微镜的观察对象不限于导体，同样适用于非导体，弥补了扫描隧道显微镜的不足，进一步拓宽了应用范围.Treacy等[8]使用透射电子显微镜观测了碳纳米管的固有热振动振幅，并由此得到了相应的杨氏模量.Krishnan等[9]利用电子显微镜研究了单壁碳纳米管在室温下的热振动现象，并得到了碳纳米管杨氏模量与其尺寸及振幅标准差之间的关系.Babic等[10]利用电子显微镜，拍摄了两端固支碳纳米管热振动图像，发现振幅随温度的升高而增加.Lee等[11]利用原子力显微镜测量了单层石墨烯的弹性性质.Bunch等[12]采用原子力显微镜和激光测量等方法，观测了单层石墨烯的振动过程，得到了固有频率和品质因子等参数.Garcia-Sanchez等[13]利用原子力显微镜研究了悬浮石墨烯振动过程，并分析了边界效应对振动行为的影响.

除了实验手段上的不断进步外，近百年来量子力学的发展为纳米科技的发展提供了理论基础，但是由于纯量子力学的计算方法计算量巨大，因此其应用范围仍然受到很大的限制.在此种背景下，分子动力学方法成为模拟纳尺度结构动力学过程的最佳工具.

1.2 分子动力学方法

自20世纪50年代中期的Fermi，Pasta和Ulam开始，经过50年代末60年代初Alder等[14]和Rahman[15]的努力，分子动力学得到迅速发展.由于计算机技术的革命性发展和算法的改进，分子动力学已成为在物理、化学、生物等多项领域有价值的研究工具.Guo等[16]采用分子动力学模拟了多壁碳纳米管振荡器中的能量耗散，发现碳纳米管层间摩擦力与其手性结构以及环境温度密切相关.Jiang等[17]以碳纳米管悬臂梁为研究对象，研究了纳米结构机械能的耗散.基于传统的连续介质理论，Yao等[18]研究了温度对碳纳米管屈曲临界载荷的影响；Shen等[19]研究了温度对碳纳米管后屈曲行为的影响.Guo等[20]的分子动力学结果表明：由于原子热运动的存在，纳尺度接触的边界上存在明显的边界效应，可能导致全新的摩擦规律.Hsieh等[21]利用分子动力学的方法研究了单壁碳纳米管的固有热振动问题.

统计物理学是研究热现象规律及相关物理性质的微观理论.经典统计物理学是以经典力学为基础的，它在历史上曾经获得过巨大的成功，在经典统计力学中，能量均分原理是联系系统温度及其平均能量的基本原理.能量均分原理能够作出定量预测，它预测热平衡时系统每个粒子每个自由度上的平均动能皆为kBT/2，其中kB为波尔兹曼常数，T为温度.尽管能量均分原理在一定条件下能够对物理现象提供非常准确的预测，但是当量子效应变得显著时，基于这一原理的结果变得不准确.尤其是在处理气体和固体比热以及热辐射等问题时，暴露出不可克服的困难，普朗克为了从微观上导出热辐射的谱密度，大胆的提出了量子假说.在量子力学建立后，对统计物理学的改造也相应地完成了，并建立起以量子力学为基础的量子统计物理学，而经典统计理论适用的条件称为经典极限条件[22].

经典分子动力学是基于经典统计理论的计算方法，在热平衡状态下，在一定统计时间内，系统符合能量均分原理.在温度足够高，经典极限条件成立，即kBT≫ħω时(ħ为归一化普朗克常数，ω为圆频率)，一般情况下可认为热噪声是白噪声，分子动力学计算结果准确.但温度较低，经典极限条件不成立，即ħω接近或大于kBT时，热平衡系统的涨落呈现量子特性，热噪声不再是白噪声，而是与频率相关.此时量子效应明显，经典分子动力学无法提供准确的热振动模拟.例如，处于低温的高频振荡器和温度趋于零时的固体热容变化等.从另一方面来说，纯量子力学方法的复杂性导致其并不适用于包含大量原子系统的动力学模拟.为了将量子统计特性包含进分子动力学方法，已经有多种在分子动力学系统中考虑量子效应的半经典方法被发展起来[2328]. Wang等[29]重新定义了等效温度以使分子动力学方法包含平均量子振动能量，但是此种方法无法给出正确的能量谱.基于分子动力学的方法，Wang等[24]利用包含符合波色--爱因斯坦统计的随机力的Langevin方程计算了量子热传导问题.Buyukdagli等[23]利用包含低频有色噪声的Langevin方程计算了复杂分子系统热容和温度的依赖关系，所得结果与量子力学计算结果十分吻合.Dammak等[26]对这一理论的数值计算方法进行了改进，计算了低温下量子效应不能被忽略时的多个问题，并与实验和经典分子动力学模拟进行了对比，结果显示量子分子动力学与实验结果吻合程度明显好于经典分子动力学结果.Savin等[30]采用半量子分子动力学方法，研究了考虑粒子间相互作用的随机动力学，并将这一方法应用于模拟不同低维纳尺度结构热力学性质和热输运.

现阶段上述半量子分子动力学方法主要用于研究纳尺度材料的热传导行为.在纳米尺度范围内，基底影响、范德华力、非线性、边界效应等对碳纳米管和石墨烯的热振动行为有明显且复杂的影响，直接关系到碳材料在纳机电结构中的应用和设计等问题.但目前关于此种因素的诸多问题尚未澄清，半量子分子动力学方法有望在这些问题上做出比经典分子动力学更准确的模拟.

1.3 连续介质理论

随着计算机技术的进步，分子模拟方法近些年得到了重大发展，它的作用逐渐从指导实验发展成为独立发现纳尺度新现象的工具，甚至在一定程度上，其结果可以作为验证新理论是否可靠的标准.理论上，一切与分子或原子运动相关的问题都可采用分子模拟的方法得到解决，但是其计算仍然要花费大量的资源和时间，并且计算规模和模拟时间也有很大的局限性.另一类理论研究方法即连续介质力学模型在解决此类问题上具有明显优势.在对单层碳纳米管屈曲性质的研究中，通过对比原子结构模型和连续壳模型结果，Yakobson等[31]发现壳模型可以较准确的估计碳纳米管的屈曲形式.他们的研究结果说明，连续介质力学理论在很大程度上仍可应用于直径尺度上只有若干原子的离散结构.随后，多种连续介质模型，包括壳模型、梁模型等被应用于研究碳纳米管的弯曲、屈曲、振动和波传播等性质.但是，传统连续介质力学无法描述原子间的长程作用力和尺寸效应，因此需要引入非局部效应. Wang等[3233]在研究单壁碳纳米管的弯曲波及纵波传播时，以轴向碳原子层间距d表征微结构尺度，建立了计及碳纳米管微结构效应的非局部Timoshenko梁模型以及非局部弹性壳模型，描述了波频散规律.对于碳纳米管和石墨烯的振动问题，也有大量的等效介质模型被建立起来[34].

原子对之间的偶极矩作用造成了较弱的范德华力[35].对于纳尺度碳材料结构，尤其是双壁碳纳米管和双层石墨烯结构，层与层之间通过范德华力连接，范德华力对多层碳材料结构的摩擦现象和动力学行为等具有明显的影响[36]，另外范德华力对系统间的能量传递也起着重要的作用[37].当结构小幅振动时，层间范德华力可等效视为线性弹簧连接. Yoon等[38]建立了考虑剪切变形和转动惯量的双壁碳纳米管的等效Timoshenko梁模型，研究了在对边简支边界条件下的固有频率，他们发现对比于Euler梁模型，当梁的长度很短时，Timoshenko梁模型预测的频率值更低.Ru等[3940]用范德华相互作用系数很好地描述了碳纳米管层间范德华力的影响，研究了碳纳米管的屈曲和振动问题.He等[41]给出了碳纳米管和石墨烯层间范德华相互作用系数的解析表达式.Wang等[24]采用复合Euler梁模型预测了悬臂双壁碳纳米管的热振动固有频率，他们发现，与分子动力学结果相比，Euler梁模型对于较短的碳纳米管和较高模态的频率预测误差较大.

由于边缘原子成键结构与内部原子不同，纳尺度结构存在明显的边界效应.边界效应对于石墨烯和碳纳米管的形态有很大的影响，Shenoy等[42]在连续介质模型中采用在边缘施加收缩力的方法模拟石墨烯的边缘效应，利用有限元方法得到了边缘翘曲的形态，并与分子动力学结果进行了对比.

2 纳尺度碳材料结构热振动问题

在对碳纳米管和石墨烯热振动的研究中，研究人员采用与分子动力学对照的方法发展了多种连续介质模型.Feng等[4344]采用分子动力学方法得到了悬臂碳纳米管的热振动谱，并与结合能量均分原理的Timoshenko梁模型结果进行了对比.Wang等[4546]利用分子动力学方法和连续介质模型，分析了碳纳米管热振动中的动力学问题，并对比了Timoshenko梁模型与Euler梁模型的结果.Liu等[47]利用分子动力学方法计算了处于惰性气体中的单层石墨烯热振动的均方根振幅，并建立了相应的连续介质板模型，发现纳尺度下石墨烯存在明显的边界效应.以上研究主要关注纳尺度结构在室温或更高温度下的热振动问题，而当温度较低时，需要考虑量子效应对热振动过程的影响.

2.1 纳尺度碳材料结构低温热振动

量子效应在纳尺度结构的某些力学问题中可能起主导作用，第一是因为纳器件工作温度一般较低;第二是因为纳器件自身具有超高的固有频率.Chaste等[48]报道了一个具有2GHz振动频率150nm长的碳纳米管的纳传感器.利用该传感器在液氮温度下进行了具有1.7yg(1yg=10−24g)分辨率的质量传感器实验.这一前所未有的灵敏传感器使我们可以分辨蛋白质、奈分子.Moser等[49]的研究表明当温度达到30mK时，基于碳纳米管的纳机械谐振器的品质因数可高达5×106.Hone等[50]发现碳纳米管声子谱的量子尺寸效应.O’Connell等[51]将一个机械振动的模态冷却到量子基态，可以在谐振器中可控地产生单个声子.Benyamini等[52]在基于碳纳米管的机械谐振器上实现了电子和声子的耦合.他们发现这种耦合可以通过改变量子点在碳纳米管机械谐振器上的位置实现打开和关闭.

碳纳米管和石墨烯的热振动固有频率可达到吉赫兹，甚至太赫兹量级，能量均分原理成立所要求的ħω≪kBT的条件在较大的温度范围内不能满足，因此在进行此类结构的热振动问题研究时需计入量子效应.Wang等[53]建立了单壁碳纳米管的等效Timoshenko梁模型，对于连续介质梁的每个振动模态，可看作频率为νn的谐振子.引入量子效应，即振子能量E取分立值[54]

式中l是区分系统所有定态的量子数.此时振子的平均分布仍然符合Maxwell--Boltzmann分布，因此，振子的平均能量为

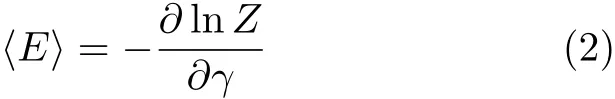
式中，Z为振子的配分函数

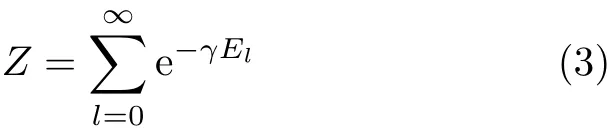
其中γ=1/kBT，将式(1)代入上式可得

将此式代入式(2)，即可得到振子的平均能量值

而当忽略量子效应，即hν≪kBT时，将上式中的指数因子展开

此时，振子的平均能量表示为

即为能量均分原理表述.

分别令式(5)和式(7)中的平均能量等于Timoshenko梁模型各阶模态的总能量，即可得到采用考虑量子效应时和经典条件下的单壁碳纳米管热振动的均方根振幅.如图2所示，随着温度的降低，结合能量均分原理的Timoshenko梁模型结果与考虑量子统计特性的Timoshenko梁模型结果之间的差值逐渐增加，量子效应更为明显.

图2 对边简支边界条件下，Timoshenko梁模型计算得到的长度为15nm的(10,10)型碳纳米管在不同温度时的热振动均方根振幅[53]

图2 对边简支边界条件下，Timoshenko梁模型计算得到的长度为15nm的(10,10)型碳纳米管在不同温度时的热振动均方根振幅[53](续)

经典连续介质模型无法得到碳纳米管结构离散性、范德华力等对热振动行为的影响，而实验方面很难进行如此小尺度、高频率的热动力学测量，故分子动力学方法成为探索此类问题、验证现有连续介质理论结果的重要工具.经典分子动力学控温方法均符合能量均分原理，需要对其进行改造，使其包含量子统计特性.Liu等[55]采用半量子分子动力学方法研究了悬臂单壁碳纳米管的低温热振动过程，得到了热振动谱和均方根振幅，并与等效Timoshenko梁模型的结果进行了对比.如图3所示，在高频段，由半量子分子动力学方法得到的能量小于由经典分子动力学方法得到的能量值，即考虑量子统计特性时，碳纳米管高频段能量被冻结.随着阶数的增加和温度的降低，由半量子分子动力学方法得到的均方根振幅与由经典分子动力学方法得到的均方根振幅差值增加，结合能量均分原理的Timoshenko梁模型与由经典分子动力学方法得到的均方根振幅值比较接近，而考虑量子统计特性的Timoshenko梁模型与半量子分子动力学方法得到的均方根振幅值比较接近.

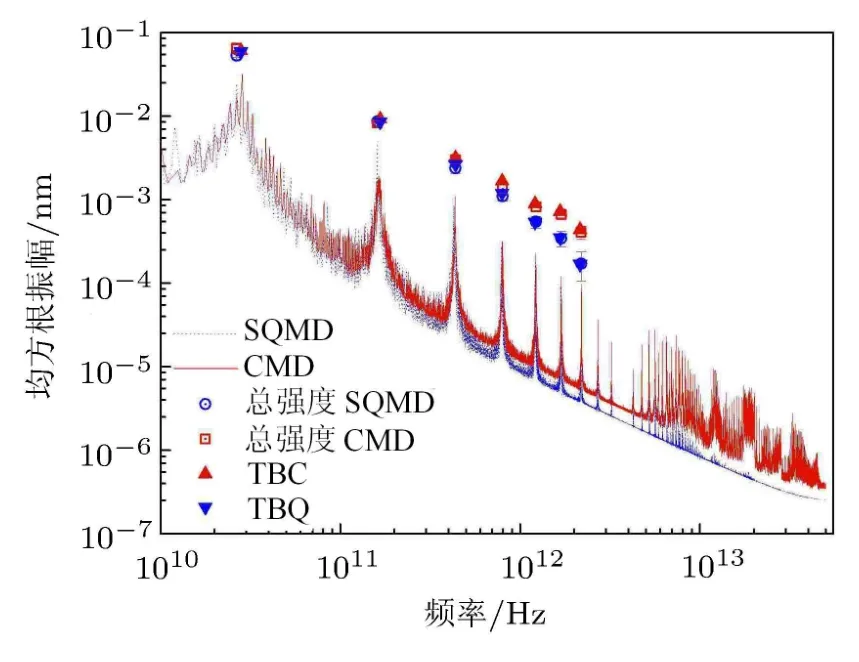
图3 长度为9.84nm的(5,5)型碳纳米管在T=35K时的热振动谱[55]

单层石墨烯是最典型的二维纳米材料，热噪声会引起石墨烯表面起伏，对其整体动力学行为起着重要的影响.Liu等[56]采用经典分子动力学方法模拟了其热振动过程，并结合能量均分原理建立了等效板模型.Wang等[5758]建立了考虑量子效应的单层石墨烯的等效板模型，分析了量子效应对四边简支矩形石墨烯和圆形石墨烯热振动的影响.Liu等[59]采用了分子动力学方法和等效板模型研究了含预应力四边固支单层石墨烯的低温热振动过程，得到了考虑量子统计特性时和经典条件下的均方根振幅和热振动谱.图4列出了单层石墨烯热振动谱和沿石墨烯中线位置的均方根振幅值.半量子分子动力学所得均方根振幅值明显小于由经典分子动力学所得结果，而两种板模型也表现出相同的变化趋势，并且板模型可较准确地预测石墨烯热振动均方根振幅值.

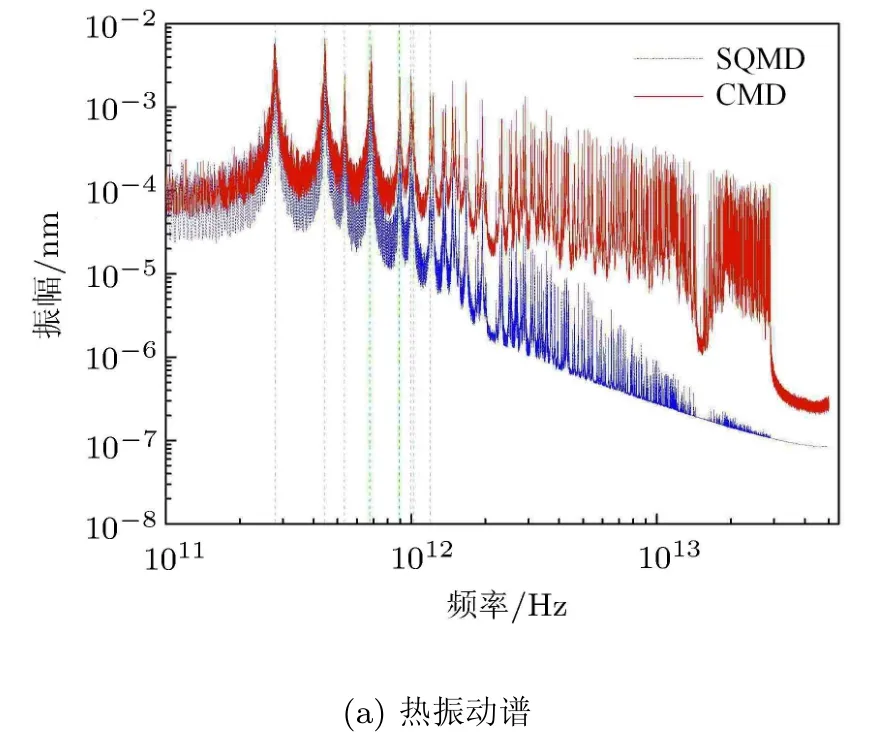
图4 温度9K时，单层石墨烯热振动谱和均方根振幅[59]

图4 温度9K时，单层石墨烯热振动谱和均方根振幅[59](续)

2.2 纳尺度碳材料非线性结构热振动

越来越多的纳机电系统应用在传感领域，如质量[6061]、力[62]等的检测.除此之外，纳器件可应用于制造时钟[63]，探测基本物理过程和动力学过程[64]的基本部件等.在小振幅范围内，其力学行为是线性的.但是，随着振幅的增加，非线性效应变得明显.非线性效应对于上述纳器件的影响至关重要[65]，例如，非线性现象关系到器件频率漂移的极限值[66].造成纳结构力学行为非线性的因素有很多，包括材料非线性[67]、边界非线性[68]、阻尼机制[69]、吸附/脱落过程[70]和几何构型影响[7172]等.当结构存在大变形时，导致应变和曲率关系出现非线性，因此产生几何非线性[73].关于碳纳米管的非线性动力学已经有理论上的研究.Ouakad等[74]研究了含几何非线性和范德华力的碳纳米管谐振器的复杂非线性动力学行为，他们研究了包括碳纳米管软化在内的非线性过程.Caruntu等[75]研究了阻尼和范德华力对悬臂碳纳米管受迫振动时的影响，对比了由多尺度方法得到的频率和保留五阶的线性梁模型的频率值.对于电压激励的碳纳米管的非线性振动，其模态间存在耦合现象[7678]，振动模式有可能从平面振动突然跳转到非平面振动[7980].并且碳纳米管的初始构型对其非线性振动有较大影响，当碳纳米管发生涡动现象时，能量有可能在模态之间交换[81].纳结构热振动振幅随温度的升高而增加，当温度较高时，过大的振幅可能导致结构产生几何非线性，并引起复杂的动力学行为[82].

Wang等[83]研究了由于热应力引起的两端简支碳纳米管的非线性热振动，随着温度的升高，碳管内部热应力增加，当达到一定温度时，碳管发生屈曲，此时碳管做非线性非平面振动.如图5所示，随着温度的升高，碳管过中心位置的概率越来越低.

图5 由非线性、非平面梁模型计算得到的长度为80nm的(10,10)型碳纳米管在x方向和y方向的热振动位移分量联合概率密度[83]

Liu等[84]采用分子动力学方法模拟了悬臂单壁碳纳米管在较长时间尺度上的热振动过程，发现碳纳米管在微正则系综系统中自由振动过程端部原子在y方向和z方向的振幅在某些时间段呈现出此起彼伏的周期性变化趋势，这意味着在两个正交的横向振动方向之间存在耦合，发生了能量交换.如图6(a)所示为模拟过程中一段时间内端部原子在y--z平面内的轨迹，每幅图的时间间隔为1.5ns.从这些连续的图像中可发现，悬臂碳纳米管在此时间段内作非平面振动，振动轨迹呈椭圆形，且椭圆随时间的变化逆时针转动，这是明显的涡动现象.图6(b)为采用等效非线性非平面梁模型计算得到的梁自由端部在y--z平面内的运动轨迹.对比这两幅图可以看出，非线性非平面梁模型可给出与分子动力学模拟类似的结果.

图6 长度为12.6nm的悬臂单壁碳纳米管自由振动端部在y--z平面内的运动轨迹[84]

3 总结及展望

现阶段，涉及纳结构热振动的研究主要集中在热传导问题、简单纳结构的复杂热振动问题等.这些研究展示了热振动中丰富的动力学现象，仍有很多问题值得关注.

受限于计算能力和分析手段的限制，目前大多数理论研究集中在分析理想边界条件下孤立的简单结构的动力学行为.但现实条件下，纳结构往往被放置于基底之上，结构以非接触的方式通过范德华力与基底相互作用.由于温度的影响，这种范德华力会发生随机波动，并且基底与结构之间可能存在相对滑移和能量传递等现象.对于此种问题，需要建立全局模型或对现有模型的边界条件进行改进.

温度是化学反应的关键因素，化学反应中常常伴随着能量的释放和吸收，因此，若所研究的纳尺度结构热振动过程存在化学反应，会导致结构局部的温度和动力学参数发生变化，此种热振动与化学反应耦合的动力学行为尚未见报道.另外，对生命结构的研究已深入脱氧核糖核酸(deoxyribono-nucleic acid,DNA)分子，从力学角度来看，DNA分子是一个复杂的多自由度非线性振动系统，热噪声对其动力学演化起着重要的影响，研究DNA分子中的热振动问题有助于理解其生物学行为.

热振动过程常常伴随着热辐射现象，而外部辐射也会对热振动产生影响.将辐射计入热振动计算模型将进一步提高结果的精确性.

对纳尺度结构热振动的研究开展的时间不长，仍然面临着较多的难题和较大的挑战.需要进一步发展实验观测手段，提高量子力学及分子动力学计算效率及适用范围，改进经典动力学模型，使之更好地预测纳尺度结构的热振动问题.

1 Nyquist H.Thermal agitation of electric charge in conductors.Physical Review,1928,32(1):110-113

2 Johnson JB.Thermal agitation of electricity in conductors.Physical Review,1928,32(1):97-109

3朱位秋.非线性随机动力学与控制.北京:科学出版社,2003

4朱位秋,黄志龙,应祖光.非线性随机动力学与控制的哈密顿理论框架.力学与实践,2002，24(3):1-9

5金大重,李昕欣,刘剑等.微机械悬臂梁中的机械噪声机制分析.传感技术学报,2007,20(1):101-106

6 Stoneham AM,Gavartin JL.Dynamics at the nanoscale.Materials Science and Engineering:C,2007,27(5-8):972-980

7 Geim AK.Graphene:status and prospects.Science,2009, 324(5934):1530-1534

8 Treacy MMJ,Ebbesen TW,Gibson JM.Exceptionally high Young’s modulus observed for individual carbon nanotubes.Nature,1996,381(6584):678-680

9 Krishnan A,Dujardin E,Ebbesen TW,et al.Young’s modulus of single-walled nanotubes.Physical Review B,1998, 58(20):14013-14019

10 Babic B,Furer J,Sahoo S,et al.Intrinsic thermal vibrations of suspended doubly clamped single-wall carbon nanotubes.Nano Letters,2003,3(11):1577-1580

11 Lee CG,Wei XD,Kysar JW,et al.Measurement of the elastic properties and intrinsic strength of monolayer graphene.Science,2008,321(5887):385-388

12 Bunch JS,van der Zande AM,Verbridge SS,et al.Electromechanical resonators from graphene sheets.Science, 2007,315(5811):490-493

13 Garcia-Sanchez D,van der Zande AM,Paulo AS,et al.Imaging mechanical vibrations in suspended graphene sheets.Nano Letters,2008,8(5):1399-1403

14 Alder BJ,Wainwright TE.Studies in molecular dynamics.I.General method.The Journal of Chemical Physics, 1959,31(2):459-466

15 Rahman A.Correlations in the motion of atoms in liquid argon.Physical Review,1964,136(2A):405-411

16 Guo WL,Guo YF,Gao HJ,et al.Energy dissipation in gigahertz oscillators from multiwalled carbon nanotubes.Physical Review Letters,2003,91(12):125501

17 Jiang H,Yu MF,Liu B,et al.Intrinsic energy loss mechanisms in a cantilevered carbon nanotube beam oscillator.Physical Review Letters,2004,93(18):185501

18 Yao XH,Han Q.Investigation of axially compressed buckling of a multi-walled carbon nanotube under temperature fi eld.Composites Science and Technology,2007,67(1): 125-134

19 Shen H,Zhang C.Postbuckling prediction of axially loaded double-walled carbon nanotubes with temperature dependent properties and initial defects.Physical Review B, 2006,74(3):035410

20 Guo ZR,Chang TC,Guo XM,et al.Thermal-induced edge barriers and forces in interlayer interaction of concentric carbon nanotubes.Physical Review Letters,2011,107(10): 105502-105504

21 Hsieh J,Lu J,Huang M,et al.Theoretical variations in the Young’s modulus of single-walled carbon nanotubes with tube radius and temperature:a molecular dynamics study.Nanotechnology,2006,17(15):3920-3924

22林宗涵.热力学与统计物理学.北京:北京大学出版社,2007

23 Buyukdagli S,Savin AV,Hu B.Computation of the temperature dependence of the heat capacity of complex molecular systems using random color noise.Physical Review E, 2008,78(6):066702

24 Wang JS,Ni XX,Jiang JW.Molecular dynamics with quantum heat baths:application to nanoribbons and nanotubes.Physical Review B,2009,80(22):224302

25 Ceriotti M,Bussi G,Parrinello M.Nuclear quantum e ff ects in solids using a colored-noise thermostat.Physical Review Letters,2009,103(3):030603

26 Dammak H,Chalopin Y,Laroche M,et al.Quantum thermal bath for molecular dynamics simulation.Physical Review Letters,2009,103(19):190601

27 Wang JS.Quantum thermal transport from classical molecular dynamics.Physical Review Letters,2007,99(16): 160601

28 Miller WH.Quantum dynamics of complex molecular systems.Proceedings of the National Academy of Sciences of the United States of America,2005,102(19):6660-6664

29 Wang CZ,Chan CT,Ho KM.Tight-binding moleculardynamics study of phonon anharmonic e ff ects in silicon and diamond.Physical Review B,1990,42(17):11276-11283

30 Savin AV,Kosevich YA,Cantarero A.Semiquantum molecular dynamics simulation of thermal properties and heat transport in low-dimensional nanostructures.Physical Review B,2012,86(6):064305

31 Yakobson BI,Brabec CJ,Bernholc J.Nanomechanics of carbon tubes:instabilities beyond linear response.Physical Review Letter,1996,76(14):2511-2514

32 Wang LF,Hu HY.Flexural wave propagation in singlewalled carbon nanotubes.Physical Review B,2005,71(19): 195412

33 Wang LF,Hu HY,Guo WL.Validation of the non-local elastic shell model for studying longitudinal waves in singlewalled carbon nanotubes.Nanotechnology,2006,17(5): 1408-1415

34 Gibson RF,Ayorinde EO,Wen YF.Vibrations of carbon nanotubes and their composites:a review.Composites Science and Technology,2007,67(1):1-28

35沈以赴.固体物理学基础教程.北京:化学工业出版社,2005

36 Vanossi A,Manini N,Urbakh M,et al.Colloquium:modeling friction:from nanoscale to mesoscale.Review of Modern Physics,2013,85(2):529-552

37 Greaney PA,Grossman JC.Nanomechanical energy transfer and resonance e ff ects in single-walled carbon nanotubes.Physical Review Letter,2007,98(12):125503

38 Yoon J,Ru CQ,Mioduchowski A.Terahertz vibration of short carbon nanotubes modeled as Timoshenko beams.Journal of Applied Mechanics-Transactions of the ASME, 2005,72(1):10-17

39 Ru CQ.E ff ective bending sti ff ness of carbon nanotubes.Physical Review B,2000,62(15):9973-9976

40 Yoon J,Ru CQ,Mioduchowski A.Vibration of an embedded multiwall carbon nanotube.Composites Science and Technology,2003,63(11):1533-1542

41 He XQ,Kitipornchai S,Liew KM.Buckling analysis of multi-walled carbon nanotubes:a continuum model accounting for van der Waals interaction.Journal of theMechanics and Physics of Solids,2005,53(2):303-326

42 Shenoy VB,Reddy CD,Ramasubramaniam A,et al.Edgestress-induced warping of graphene sheets and nanoribbons.Physical Review Letters,2008,101(24):245501

43 Feng EH,Jones RE.Carbon nanotube cantilevers for nextgeneration sensors.Physical Review B,2011,83(19): 195412

44 Feng EH,Jones RE.Equilibrium thermal vibrations of carbon nanotubes.Physical Review B,2010,81(12):125436

45 Wang LF,Hu HY.Thermal vibration of double-walled carbon nanotubes predicted via double-Euler-beam model and molecular dynamics.Acta Mechanica,2012,223(10):2107-2115

46 Wang LF,Hu HY,Guo WL.Thermal vibration of carbon nanotubes predicted by beam models and molecular dynamics.Proceedings of the Royal Society of London,Series A：Mathematical,Physical and Engineering Sciences, 2010,466(2120):2325-2340

47 Liu RM,Wang LF.Stochastically driven vibrations of single-layered graphene sheets.Science China-Physics Mechanics&Astronomy,2012,55(6):1103-1110

48 Chaste J,Eichler A,Moser J,et al.A nanomechanical mass sensor with yoctogram resolution.Nature Nanotechnology, 2012,7(5):300-303

49 Moser J,Eichler A,Guettinger J,et al.Nanotube mechanical resonators with quality factors of up to 5 million.Nature Nanotechnology,2014,9(12):1007-1011

50 Hone J,Batlogg B,Benes Z,et al.Quantized phonon spectrum of single-wall carbon nanotubes.Science,2000, 289(5485):1730-1733

51 O’Connell AD,Hofheinz M,Ansmann M,et al.Quantum ground state and single-phonon control of a mechanical resonator.Nature,2010,464(7289):697-703

52 Benyamini A,Hamo A,Kusminskiy SV,et al.Real-space tailoring of the electron-phonon coupling in ultraclean nanotube mechanical resonators.Nature Physics,2014,10(2): 151-156

53 Wang LF,Hu HY.Thermal vibration of single-walled carbon nanotubes with quantum e ff ects.Proceedings of the Royal Society A:Mathematical,Physical and Engineering Sciences,2014,470(2168):20140087

54 Lahiri A.Statistical Mechanics:An Elementary Outline. India:Universities Press Private Ltd,2009

55 Liu RM,Wang LF.Thermal vibration of a single-walled carbon nanotube predicted by semiquantum molecular dynamics.Physical Chemistry Chemical Physics,2015,17(7): 5194-5201

56 Liu RM,Wang LF.Stochastically driven vibrations of single-layered graphene sheets.Science China—Physics Mechanics&Astronomy,2012,55(6):1103-1110

57 Wang LF,Hu HY.Thermal vibration of a circular singlelayered graphene sheet with simply supported or clamped boundary.Journal of Sound and Vibration,2015,349(4): 206-215

58 Wang LF,Hu HY.Thermal vibration of a rectangular single-layered graphene sheet with quantum e ff ects.Journal of Applied Physics,2014,115(23):233515

59 Liu RM,Wang LF,Jiang JN.Thermal vibration of a singlelayered graphene with initial stress predicted by semiquantum molecular dynamics.Materials Research Express, 2016,3(9):095601

60 Naik AK,Hanay MS,Hiebert WK,et al.Towards singlemolecule nanomechanical mass spectrometry.Nature Nanotechnology,2009,4(7):445-450

61 Dohn S,Svendsen W,Boisen A,et al.Mass and position determination of attached particles on cantilever based mass sensors.Review of Scienti fi c Instruments,2007, 78(10):103303

62 San Paulo A,Garcia R.Tip-surface forces,amplitude, and energy dissipation in amplitude-modulation(tapping mode)force microscopy.Physical Review B,2001,64(19): 193411

63 Villanueva LG,Karabalin RB,Matheny MH,et al.A nanoscale parametric feedback oscillator.Nano Letters, 2011,11(11):5054-5059

64 Karabalin RB,Lifshitz R,Cross MC,et al.Signal ampli fication by sensitive control of bifurcation topology.Physical Review Letters,2011,106(9):094102

65 Sato M,Hubbard BE,Sievers AJ.Colloquium:nonlinear energy localization and its manipulation in micromechanical oscillator arrays.Review of Modern Physics,2006, 78(1):137-157

66 Cleland AN,Roukes ML.Noise processes in nanomechanical resonators.Journal of Applied Physics,2002,92(5): 2758.

67 Kaajakari V,Mattila T,Oja A,et al.Nonlinear limits for single-crystal silicon microresonators.Journal of Microelectromechanical Systems,2004,13(5):715-724

68 Tabaddor M.In fl uence of nonlinear boundary conditions on the single-mode response of a cantilever beam.International Journal of Solids and Structures,2000,37(36): 4915-4931

69 Eichler A,Moser J,Chaste J,et al.Nonlinear damping in mechanical resonators made from carbon nanotubes and graphene.Nature Nanotechnology,2011,6(6):339-342

70 Atalaya J,Isacsson A,Dykman MI.Di ff usion-Induced bistability of driven nanomechanical resonators.Physical Review Letters,2011,106(22):227202

71 Crespo da Silva MRM,Glynn CC.Nonlinear fl exuralfl exural-torsional dynamics of inextensional beams.I. Equations of motion.Journal of Structural Mechanics, 1978,6(4):437-448

72 Crespo da Silva MRM,Glynn CC.Nonlinear fl exuralfl exural-torsional dynamics of inextensional beams.II. Forced motions.Journal of Structural Mechanics,1978, 6(4):449-461

73 Villanueva LG,Karabalin RB,Matheny MH,et al.Nonlinearity in nanomechanical cantilevers.Physical Review B, 2013,87(2):024304

74 Ouakad HM,Younis MI.Nonlinear dynamics of electrically actuated carbon nanotube resonators.Journal of Computational and Nonlinear Dynamics,2010,5(1):011009

75 Caruntu DI,Luo L.Frequency response of primary resonance of electrostatically actuated CNT cantilevers.Nonlinear Dynamics,2014,78(3):1827-1837

76 Castellanos-Gomez A,Meerwaldt HB,Venstra WJ,et al. Strong and tunable mode coupling in carbon nanotube resonators.Physical Review B,2012,86(4):41402

77 Eichler A,Del Alamo Ruiz M,Plaza JA,et al.Strong coupling between mechanical modes in a nanotube resonator.Physical Review Letter,2012,109(2):25503

78 Sonne G,Shekhter RI,Gorelik LY,et al.Superconducting pumping of nanomechanical vibrations.Physical Review B,2008,78(14):144501

79 Dequesnes M,Rotkin SV,Aluru NR.Parameterization of continuum theories for single wall carbon nanotube switches by molecular dynamics simulations.Journal of Computational Electronics,2002,1(3):313-316

80 Conley WG,Raman A,Krousgrill CM,et al.Nonlinear and nonplanar dynamics of suspended nanotube and nanowire resonators.Nano Letters,2008,8(6):1590-1595

81 Behboud A,Scott RA.Whirling motions of a beam generated by in-plane pulses.Journal of Sound and Vibration, 1992,152(1):183-188

82 Koh H,Cannon JJ,Shiga T,et al.Thermally induced nonlinear vibration of single-walled carbon nanotubes.Physical Review B,2015,92(2):024306

83 Wang LF,Hu HY.Thermal vibration of a simply supported single-walled carbon nanotube with thermal stress.Acta Mechanica,2016,227(7):1957-1967

84 Liu RM,Wang LF.Coupling between fl exural modes in free vibration of single-walled carbon nanotubes.AIP Advance, 2015,5(12):127110

(责任编辑:胡漫)

THERMAL VIBRATION OF TYPICAL NANO-STRUCTURE1)

LIU RumengWANG Lifeng2)
(State Key Laboratory of Mechanics and Control of Mechanical Structures,Nanjing University of Aeronautics and Astronautics, Nanjing 210016,China)

The thermal vibration is the inherent vibration of nanostructures,which plays an important role in the dynamics of nanostructures.The quantum e ff ects,the boundary e ff ects and the van der Waals interaction have a signi fi cant in fl uence on the thermal vibration of nanostructures.The carbon nanotubes and the graphene were extensively studied for their novel electronic properties and superior mechanical strength.This paper reviews some research methods for the thermal vibration of nanostructures,the thermal vibration of the carbon nanotube and the graphene in low temperatures and the nonlinear thermal vibration of the carbon nanotube.

graphene,carbon nanotube,thermal vibration,quantum e ff ects,nonlinear vibration

V412.4

A

10.6052/1000-0879-16-429

2016–12–28收到第1稿，2017–01–03收到修改稿.

1)国家自然科学基金(11522217)、江苏省333高层次人才培养工程和中央高校基本科研业务费专项资金资助.

刘汝盟,王立峰.典型纳尺度结构的热振动.力学与实践,2017,39(2):109-119 Liu Rumeng,Wang Lifeng.Thermal vibration of typical nano-structure.Mechanics in Engineering,2017,39(2): 109-119