5-1/2FH钻杆接头极限承载能力研究1)

祝效华张智

(西南石油大学机电工程学院，成都610500)

5-1/2FH钻杆接头极限承载能力研究1)

祝效华2)祝效华，教授，主要从事管柱力学及井下工具设计方面的研究工作.E-mail：zxhth113@163.com张智3)张智，硕士研究生.主要从事井下工具及力学相关方面的研究.

(西南石油大学机电工程学院，成都610500)

随着超深井、定向井、水平井、大位移井及大斜度井在石油钻井工程中的广泛应用，由井下复杂工况引起的钻杆接头过早失效问题日益突出，导致钻井周期增长，成本增加，成为制约钻井工程效益的主要因素之一.近年来，不少学者对钻杆接头进行了大量研究，多数采用二维轴对称模型，少数采用三维力学模型，但并未同时考虑螺纹升角和井眼弯曲作用等因素的影响，而钻杆接头的极限承载能力研究更是鲜见报道.针对上述问题，基于虚功原理、von Mises屈服原则及接触非线性理论，同时考虑螺纹升角和井眼弯曲作用，建立了钻杆接头的三维数值仿真模型与井眼曲率到加载弯矩的转换模型，研究了钻杆接头的上扣特性、井眼曲率对连接强度和密封性能的影响，考虑预紧力、弯曲载荷及动载安全系数，计算了钻杆接头的极限工作拉力和极限工作扭矩.研究结果表明：上扣扭矩使钻杆接头产生一定的初始接触压力，保证钻杆接头井下作业过程中的连接强度与密封性能；井眼曲率对钻杆接头井下作业过程中的连接强度与密封性能影响极大，常见的某些工况会导致钻杆接头的连接强度和密封性能丧失，考虑服役时的随机振动与冲击，常规的超深井、水平井、定向井、大位移井及大斜度井弯曲段钻杆接头的设计和选型应着重考虑井眼曲率的影响；针对设计的每种钻杆接头，都应考虑常见的井眼曲率和轴向拉伸载荷进行极限工作拉力和极限工作扭矩的精细化数值计算，以确保其安全工作.

钻杆接头,上扣特性,井眼曲率,连接强度,密封性能,工作安全性

钻杆接头的过早失效问题是钻井工程中常见的难题.在钻井过程中，钻杆接头处于相当重要的地位，其工作环境恶劣，受力十分复杂，它往往是钻井工具中最为薄弱的环节之一[1].近年来，随着能源需求量的增加，在超深井、水平井、定向井、大位移井及大斜度井旋转钻进模式下钻杆接头过早失效问题越发突出.据权威部门统计，全国油(气)田每年至少发生500起钻柱失效事故，直接经济损失达4000万元以上，其中绝大多数失效事故与钻杆接头密切相关[2].

国内外油(气)井钻杆接头的失效问题相当严重，在整个钻杆组件失效中，钻杆接头失效约占60%，其他部位失效约占40%[3].一旦发生失效事故，轻则停工打捞，费时耗力；重则导致全井报废，造成严重的经济损失.国内外很早就对钻杆接头作了大量研究，在大量理论与实验的基础上建立了较为合理的力学模型，可以对钻杆接头的力学性能进行比较准确的预测.狄勤丰等[4]建立了双台肩钻杆接头的三维力学模型，研究了双台肩钻杆接头在上扣扭矩、轴向拉力与弯矩作用下的力学性能；李明等[5]建立了钻具接头的二维轴对称模型，对钻具接头螺纹应力分布与结构优化展开了深入研究；明鑫等[6]针对气体携岩对钻杆接头的冲蚀规律进行了深入研究；庄泳等[7]建立了钻杆接头二维轴对称力学模型，分析了钻杆接头在不同紧扣圈数及拉伸载荷下的受力；Shahani等[8]对钻杆接头接触应力和拉伸应力集中系数进行了数值模拟研究；Korin等[9]提出在接头应力最大处引入可控的残余压应力，以缓解疲劳裂纹的产生；Akyildiz等[10]通过实验的方法研究了加工参数对螺纹接头连接强度的影响；Tikhonov等[11]研究了超深井中钻杆接头的腐蚀问题，通过实验得出了材料的S-N曲线，定义了钻杆接头的应力集中系数，通过数值计算获得了接触面和交界面的摩擦系数.上述研究主要集中于二维轴对称模型，少数采用三维力学模型，但并未同时考虑螺纹升角和井眼弯曲作用，无法准确反映实际工况条件下的力学性能.针对钻杆接头的极限承载能力研究更是鲜有报道.

针对上述问题，基于虚功原理、von Mises屈服原则及接触非线性理论，同时考虑螺纹升角和井眼弯曲作用，建立了钻杆接头的三维数值仿真模型和井眼曲率到加载弯矩的理论转换模型，研究了钻杆接头的上扣特性，井眼曲率对连接强度和密封性能的影响，综合考虑预紧力、弯曲载荷和动载安全系数，通过大量数值计算，绘制钻杆接头的极限工作拉力图版和极限工作扭矩图版.

1 钻杆接头分析力学原理

钻井过程中，钻杆接头受力一般处于弹性范围内，在井下多工况作用下的力学行为可视为复杂的空间弹性问题.考虑工程安全性，以屈服极限为判别标准，数值计算时采用Hook定理.假定整个过程受力连续稳定，且将钻杆接头视为各向同性的均质体，根据广义虎克定律可推导出钻杆接头的弹性应变增量本构方程[12]

式中，G为剪切模量，Pa；Sij为Kirchho ff应力张量，Pa；σm为静水压力，Pa；K为体积弹性模量，Pa；δij为Kronecker符号.

根据Euler应力张量和Kirchho ff应力张量表示的相互转化关系，可推导出钻杆接头连接螺纹的有限元控制方程[13]

式中,σij为Euler应力张量，Pa；δεij为虚应变；A为现时构型中的表面积，m2；V0为初始构型中的体积，m3；fi为单位表面力载荷，N；δui为虚位移，m.

2 钻杆接头数值仿真模型

2.1 钻杆接头三维数值仿真模型

以API 5 1/2 FH(φ177.8mm×101.6mm)钻杆接头[14]为对象，基于螺纹接头三维分析评价技术，建立钻杆接头的三维数值仿真模型.钻杆接头材料为37CrMnMo，弹性模量为206GPa，泊松比为0.28，屈服强度为931MPa，抗拉强度为1080MPa.考虑螺纹脂的影响，在数值计算过程中，摩擦系数取0.08[15].

为了提高计算效率和保证计算结果精度，对模型进行假设：(1)钻杆接头视为各向同性、连续的均质体；(2)不考虑钻杆接头硬化和蠕变带来的影响.采用Abaqus/explicit有限元程序中的C3D8R六面体单元对钻杆接头进行网格单元划分.由于螺纹部分属于高应力区，因此对其进行网格细化处理，以确保计算精度，其最小控制尺寸为1，非螺纹连接部分的最大控制尺寸设为10，以提高计算效率.钻杆接头共划分网格单元106080个，公扣54720个，母扣51360个，数值仿真模型如图1所示.

图1 钻杆接头数值仿真模型

边界条件：在外螺纹非螺纹端面中心建立参考点，使其与端面进行kinematic耦合，在该参考点施加固支边界，消除自由度.在内螺纹非螺纹端面中心建立参考点，将其与端面kinematic耦合，在该参考点施加外载荷.考虑几何非线性和接触非线性的存在，计算中将几何非线性开关打开，采用罚函数法定义库伦摩擦形式的接触条件.由于钻杆接头在受扭矩载荷作用时，其接触表面是不断变化的，呈现高度接触非线性状态.Abaqus/explicit为解决这类高度接触非线性问题提供了两种接触处理：一种是面面接触；另一种是通用接触.本文采用通用接触来设置接头啮合面间的接触关系，控制表面间的容纳极限，从而使整个接触分析精确稳定.

2.2 数值仿真模型验证

为了确保计算结果的可靠性，首先建立了与文献[16]规格相同的连接螺纹数值仿真模型，研究了实验工况(轴向拉力1200.96kN)下接箍外缘处的应力分布，模拟结果与实验结果对比如图2所示.从图中可以看出，模拟结果和实验结果趋势相同，最大误差为5.75%，进而验证了本文三维数值仿真模型建模方法的精确性.

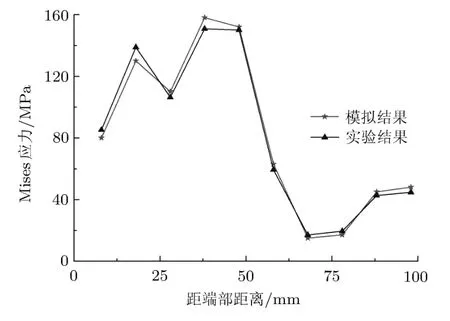
图2 模拟结果和实验结果对比

3 钻杆接头上扣特性分析

3.1 上扣过程与受力特征

为了保证钻杆接头在井下作业时的连接强度和密封能力，首先对钻杆接头进行预紧上扣，上扣如图3所示.上扣过程控制：(1)保证公扣与母扣的对中性，防止因对中性不足造成的过上扣；(2)控制上扣扭矩达到最佳上扣扭矩，防止上扣不足.

图3 钻杆接头上扣过程示意图

钻杆接头二维轴对称模型忽略了螺纹牙的螺旋升角，各螺纹牙相互独立，在扭矩载荷作用下，公扣将相对于母扣持续转动，无法完成钻杆接头上扣特性分析.钻杆接头三维力学模型的优点在于考虑了螺纹牙的螺旋升角，可以有效模拟扭矩载荷作用下的应力特性.在上扣扭矩作用下，公扣沿着母扣螺旋方向运动直到拧紧，从而实现钻杆接头的预紧上扣，钻杆接头受力特征如图4所示.

图4 上扣扭矩作用下钻杆接头受力特征

3.2 上扣扭矩下的应力特征

根据API RP-7G规定[17]：计算过程中钻杆接头上扣推荐水平为496.6MPa，上扣扭矩是基于上扣到危险截面发生屈服的60%基础上的，在正常上扣过程中螺纹本身并不会发生破坏.对钻杆接头施加45kN·m的上扣扭矩，采用平滑的直线加载，利用Abaqus/explicit模拟钻杆接头的上扣过程，完成钻杆接头的上扣特性分析，结果如图5所示.

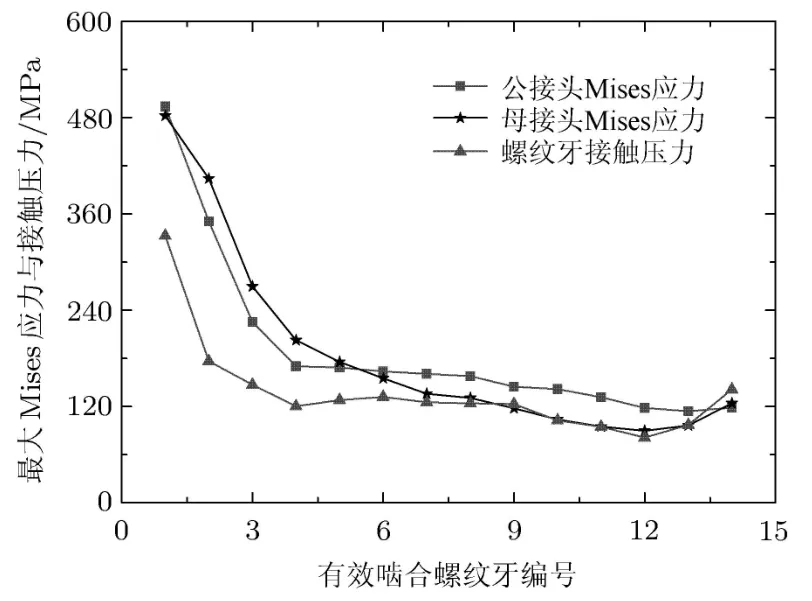
图5 最大Mises应力和接触压力分布

图5给出了上扣扭矩作用下钻杆接头各有效啮合螺纹牙的最大Mises应力和接触压力.从图中可以看出，在上扣扭矩作用下，钻杆接头上的Mises应力分布极其不均匀，公扣和母扣第一有效啮合螺纹牙根附近呈现显著的应力集中现象.在上扣扭矩作用下，钻杆接头的最大Mises应力为493.78MPa.根据API RP 7G推荐，上扣扭矩在钻杆接头上产生的初始应力为504MPa[18].数值模拟计算结果与标准规定之间的弹性应力误差约为2.03%，进一步验证了模型的精确性.上扣扭矩使钻杆接头接触面间产生了一定的初始接触压力，保证了钻井过程中的连接强度与密封性能.

4 弯曲段钻杆接头力学特性

4.1 弯曲段钻杆接头弯矩载荷计算

在钻井过程中，当钻杆接头经过弯曲段时，会承受井眼轨迹形成的弯矩载荷.为了分析井眼曲率对钻杆接头力学性能的影响，需将井眼曲率转化为弯矩，从而在钻杆接头载荷边界条件上施加弯矩载荷.假设钻杆接头与井眼轨迹同轴线，根据经典平面弹性梁理论，可得井眼弯曲段钻杆接头的曲率计算模型[19]

式中，ρ为井眼曲率半径，m；M为钻杆接头承受弯矩，N·m；E为弹性模量，Pa；Iz为钻杆接头极惯性矩，m4.

式(3)是纯弯曲条件下的模型，且此处仅仅是为了将井眼曲率转换为可施加的弯矩载荷，并不受其他条件限制，因而适用于此.钻杆接头在井眼弯曲段的弯曲情形可视为与梁结构相同的弯曲状态，通过图6可计算出钻杆接头在弯曲井段的曲率半径ρ.将曲率半径计算式(4)代入式(3)，可推导出0◦/(30m)～90◦/(30m)井眼曲率到加载弯矩的转换模型，如式(5)所示

式中,k为井眼曲率，(◦/(30m)).

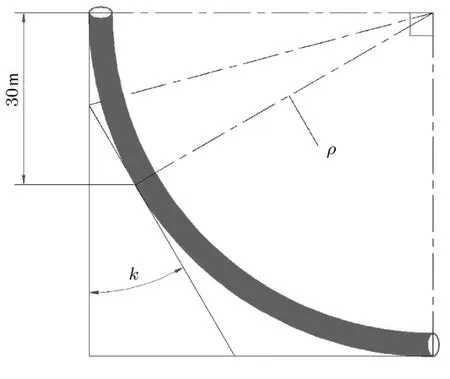
图6 井眼曲率半径计算模型示意图

实际工程中，φ177.8mm×101.6mm的钻杆接头常用于钻直径为φ311mm的井眼，这种井眼的造斜率极少超过10◦/(30m)，但考虑到中长半径井眼的造斜率一般为2◦/(30m)～20◦/(30m)，因此通过弯矩载荷计算模型计算出了20◦/(30m)以内井眼曲率对应的弯矩，如表1所示.表中数据将作为后续分析的弯矩载荷，也可为现场中长半径井眼曲率井眼钻杆接头的设计和选型提供理论依据.

表1 不同井眼曲率时钻杆接头弯矩载荷

4.2 井眼曲率对钻杆接头的影响

以NP1-86井为例，当评价NP1-86井东一段产能时，计算得出弯曲段钻杆接头承受的轴向拉伸载荷为1000kN，工作扭矩为15kN·m，造斜率平均为1.6◦/(30m).考虑井底敞口和钻井液的冷却作用，忽略内外压差和井眼温度的影响.对紧扣(上扣扭矩45kN·m)后的钻杆接头施加拉、弯、扭复合载荷(轴向拉力1000kN、扭矩15kN·m、井眼曲率分别取0◦/(30m),4◦/(30m),8◦/(30m),12◦/(30m), 16◦/(30m)和20◦/(30m))，分析井眼曲率对钻杆接头连接强度与密封性能的影响，结果如图7～图9所示.

图7给出了不同井眼曲率时钻杆接头的最大Mises应力和轴向位移.从图中可以看出，公扣最大Mises应力大于母扣最大Mises应力，公扣最大轴向位移大于母扣最大轴向位移，在井眼曲率20◦/(30m)时情形相反.随着井眼曲率的增大，公扣最大Mises应力、母扣最大Mises应力、公扣最大轴向位移及母扣最大轴向位移均呈现不断增大的趋势.当井眼曲率从0◦/(30m)～20◦/(30m)变化时，公扣最大Mises应力增大11.38%，母扣最大Mises应力增大15.49%，公扣最大轴向位移增大77.78%，母扣最大轴向位移增大363.64%.由此可见，井眼曲率对钻杆接头的连接性能影响极大.

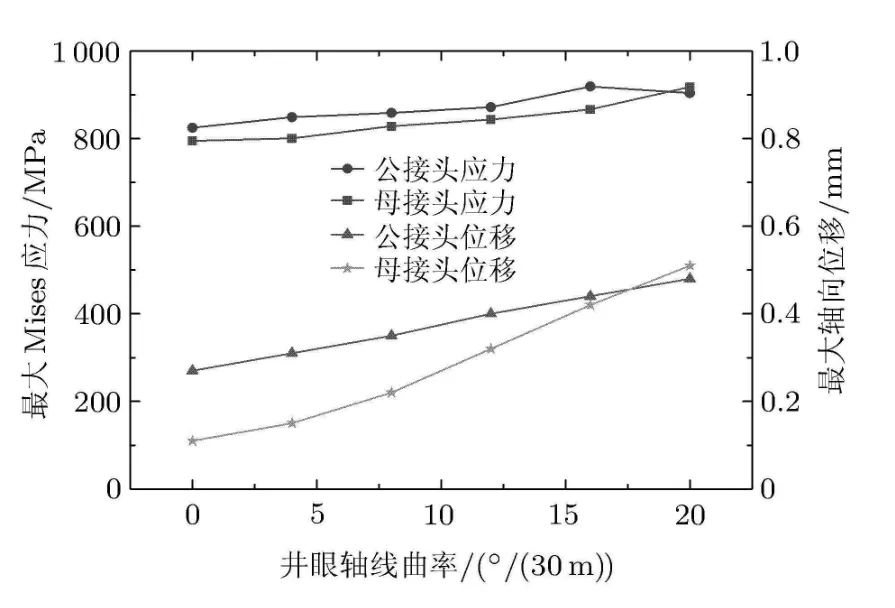
图7 不同井眼曲率时最大Mises应力与轴向位移

图8给出了不同井眼曲率时公扣第一有效啮合螺纹牙周向Mises应力分布.从图中可以看出，井眼曲率使钻杆接头螺纹一边受拉，一边受压.最大Mises应力出现在拉伸边中轴附近，最小Mises应力出现在压缩边中轴附近.随着井眼曲率的增加，钻杆接头螺纹牙周向Mises应力分布波动越剧烈，拉伸边应力逐渐增大，压缩边应力逐渐减小.这种周向应力分布不均的现象可能会降低钻杆接头抗挤压能力.由此可见，超深井、水平井、定向井、大位移井及大斜度井弯曲段钻杆接头的设计和选型应着重考虑井眼曲率的影响.

图8 公扣第一有效啮合螺纹牙周向Mises应力

图9给出了不同井眼曲率时钻杆接头台肩上的周向接触压力分布.从图中可以看出，井眼曲率使台肩预紧力一侧被释放，一侧被加强.最大接触压力出现在加强侧中轴附近，最小接触压力出现在释放侧中轴附近.随着井眼曲率增大，台肩上的周向接触压力分布不均匀性加剧，台肩上释放侧的接触压力逐渐减小，加强侧的接触压力逐渐增大.当井眼曲率从0◦/(30m)～20◦/(30m)变化时，台肩上的最小接触压力降为119.22MPa，最大接触压力增大到750.80MPa.这种周向接触压力的过度非均匀性分布降低了钻杆接头的密封性能.

图9 台肩周向接触压力分布

4.3 极限工作拉力图版

在正常钻井作业中，考虑内外压差的平衡性和钻井液的冷却作用，忽略内外压差和井眼温度的影响.由于井眼曲率对钻杆接头的井下作业安全性影响较大，为了给现场安全施工提供理论依据，计算了不同井眼曲率时钻杆接头的极限工作拉力.考虑钻井时的动载作用，取1.3的安全系数[20]，界定出钻杆接头的工作安全区、警告区和危险区，钻杆接头的极限工作拉力图版如图10所示.

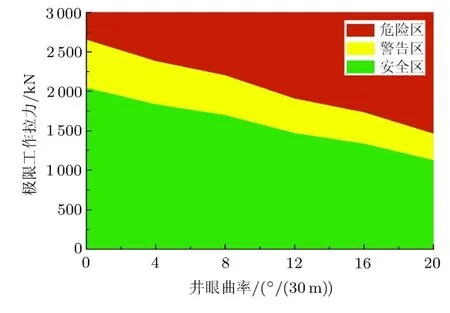
图10 钻杆接头极限工作拉力图版

图10给出了不同井眼曲率时钻杆接头的极限工作拉力图版.从图中可以看出，图版分为3个区域：黑色对应危险区，白色对应警告区、灰色对应安全区.灰色和白色区域之间的分界线即为钻杆接头的轴向极限工作拉力.通过极限工作拉力可以计算出造斜点以下的极限钻进深度.随着井眼曲率的增大，轴向极限工作拉力逐渐降低.考虑服役时的随机振动与冲击，针对设计的每种钻杆接头，都应考虑常见的井眼曲率进行极限工作拉力的精细化数值计算，以判断该型接头能否满足设计井筒长度的悬挂能力要求.在实际应用中，应尽可能使实际轴向工作拉力落在图中灰色区域.对图中安全区与警告区的分界线进行二次多项式拟合，可拟合得到钻杆接头在不同弯曲井眼中的极限工作拉力连续型理论计算模型

4.4 极限工作扭矩图版

卡钻是钻井过程中最为常见的井下难题之一.在卡钻时的解卡作业中，大轴向载荷上提钻柱是普遍的做法.顶驱的出现使得上提过程同时旋转钻杆成为可能，提高了解卡作业能力，但不当的解卡作业扭矩会导致钻杆接头失效.针对上述问题，计算出了钻杆接头的极限工作扭矩，为卡钻时解卡作业扭矩的选取提供了理论依据.考虑井下动载作用的影响，取1.3的安全系数，界定出工作安全区、警告区和危险区，钻杆接头的极限工作扭矩图版如图11所示.

图11 钻杆接头极限工作扭矩图版

图11给出了不同拉伸载荷时钻杆接头的极限工作扭矩图版.从图中可以看出，图版黑色对应危险区，白色对应警告区、灰色对应安全区.灰色和白色区域之间的分界线即为钻杆接头的极限工作扭矩.通过极限工作扭矩可以合理地进行解卡作业扭矩与钻井工作扭矩的选取.随着轴向拉伸载荷的增大，极限工作扭矩逐渐降低.由此可见，针对设计的每种钻杆接头，都应考虑常见的轴向拉伸载荷进行极限工作扭矩的精细化数值计算，以确保工作扭矩和解卡作业扭矩处于安全范围内.推荐操作：尽可能使实际钻井作业扭矩和解卡作业扭矩落在图中灰色区域.对图中安全区与警告区分界线进行二次多项式拟合，可拟合得到钻杆接头的极限工作扭矩连续型理论计算模型

式中,Mmax极限工作扭矩，kN·m；F为轴向拉伸载荷，kN.

5 结论

(1)考虑螺纹升角和井眼弯曲作用的影响，建立了钻杆接头的三维数值仿真模型与井眼曲率到加载弯矩的转换模型，突破了二维轴对称模型不能准确分析弯矩载荷、扭矩载荷及复合载荷的局限性.

(2)井眼曲率对钻杆接头的连接性能影响极大，导致钻杆接头螺纹周向Mises应力和台肩周向接触压力过度非均匀性分布，大大降低了钻杆接头的抗挤压能力和密封性能.

(3)综合考虑上扣扭矩、弯曲载荷与动载安全系数，经过大量数值计算，绘制了钻杆接头的极限工作拉力图版和极限工作扭矩图版，为计算造斜点以下的极限钻进深度与解卡作业扭矩的选取提供了理论依据.

(4)考虑钻杆使用中的随机振动与冲击，设计每种钻杆接头时都应考虑常见的井眼曲率和轴向拉伸载荷,进行极限工作拉力和极限工作扭矩的精细化数值计算，以确保其安全工作.

1袁鹏斌,陈锋,王秀梅.应力释放槽对钻杆接头力学性能的影响.石油钻探技术,2010,38(3):32-35

2董亮亮.抗弯钻杆接头螺纹及弯曲疲劳行为研究.[博士论文].成都:西南石油大学,2015

3陈松林.钻杆螺纹失效分析及改进措施研究.[硕士论文].重庆:重庆大学,2008

4狄勤丰,陈锋,王文昌等.双台肩钻杆接头三维力学分析.石油学报,2012,33(5):871-877

5李明,严仁田,鲜奇飚等.钻具接头螺纹应力分析与结构优化.重庆科技学院学报(自然科学版),2012,14(5):118-121

6明鑫,练章华,林铁军等.气体携岩对钻杆接头冲蚀规律研究.西南石油大学学报(自然科学版),2014,36(3):173-178

7庄泳,鲁喜宁,高连新等.气密钻杆接头受力分析与紧扣圈数优选.石油机械,2015,43(7):30-35

8 Shahani AR,Shari fiSMH.Contact stress analysis and calculation of stress concentration factors at the tool joint of a drill pipe.Materials and Design,2009,30(9):3615-3621

9 Korin I,Ipi˜na JP.Controlled residual stresses introduction to improve fatigue resistance of rotary shouldered connections used in oil drilling industry.International Journal of Pressure Vessels and Piping,2010,87(12):696-703

10 Akyildiz HK,Livatyali H.E ff ects of machining parameters on fatigue behavior of machined threaded test specimens.Materials and Design,2010,31(2):1015-1022

11 Tikhonov V,Kultsep A,Alikin R,et al.Application,calculation and experimental evaluation of SCF for Aluminum drill pipe with steel connector.ASME 2010 29th International Conference on Ocean,O ff shore and Arctic Engineering,2010

12刘土光,张涛.弹塑性力学基础理论.武汉:华中科技大学出版社,2008

13杨勇,柯映林,董辉跃.高速切削有限元模拟技术研究.航空学报,2006,27(3):531-535

14李新勇,赵志平,王华栋等.螺纹实用手册.北京:机械工业出版社,2009

15陈锋,狄勤丰,欧阳彦辉等.双台肩钻杆接头副台肩间隙的优选.工程力学,2013,30(S1):353-357

16王俐,张汝忻,邹家祥等.API套管圆螺纹套管接头应力场分布实验.北京科技大学学报,2000,22(6):555-558

17 American Petroleum Institute.Standard API RP 7G:Recommended Practice for Drill Stem Design and Operating Limits.American Petroleum Institute,1998

18胡辛禾.钻杆接头用的螺纹脂试验.国外石油机械,1994,5(2): 68-72

19刘鸿文.材料力学(第5版).北京:高等教育出版社,2011

20陈平.钻井与完井工程.北京:石油工业出版社,2005

(责任编辑:周冬冬)

THE ULTIMATE BEARING CAPACITY OF THE 5-1/2 FH DRILL PIPE JOINT1)

ZHU Xiaohua2)ZHANG Zhi3)
(Mechatronical Engineering School,Southwest Petroleum University,Chengdu 610500,China)

With the wide applications of the logging technologies of the ultra-deep well,the horizontal well,the directional well,the extended-reach well and the highly-deviated well in the petroleum drilling engineering,the premature failure of the drill pipe joint caused by underground complex working conditions becomes increasingly a prominent issue,and it results in the increase of the drilling period and the drilling cost,as well as the reduction of the drilling efficiency.In recent years,the drill pipe joint was extensively studied,mainly focusing on the 2D axisymmetric model,with a few on the 3D mechanical model,but without consideration of the in fl uence of the angle of thread and the bending of the hole at the same time.The ultimate bearing capacity of the drill pipe joint was not well studied.In this paper,a 3D numerical simulation model of the drill pipe joint and a model toconvert the borehole curvature to the loading moment are established based on the principle of the virtual work, the von Mises yield criterion and the nonlinear contact theory,taking account of the in fl uence of the angle of thread and the bending of the hole at the same time.The make-up property of the drill pipe joint is studied,as well as the in fl uences of the borehole curvature on the connection strength and the sealing property of the drill pipe joint,and the ultimate working pull and the ultimate working torque of the drill pipe joint are calculated with consideration of the preload,the bending load and the dynamic load safety factor.It is shown that the make-up torque can provide a certain initial contact pressure to ensure the connection strength and the sealing property of the drill pipe joint in the process of the downhole operation.The borehole curvature has a great in fl uence on the connection strength and the sealing property of the drill pipe joint in the process of the downhole operation.The connection strength and the sealing property of the drill pipe joint will be much a ff ected under some common operating conditions.In consideration of the random vibration and the shock of service,the drill pipe joint used for the common ultra-deep well,the horizontal well,the directional well,the extended-reach well and the highly deviated well should be designed and selected with due consideration of the in fl uence of the borehole curvature.For each kind of drill pipe joint to be designed,the accurate numerical calculation of the ultimate working pull and the ultimate working torque should be conducted for the corresponding borehole curvature and the axial tensile load to ensure safety.

drill pipe joint,make-up property,borehole curvature,connection strength,sealing performance, work safety

TE921.2

A

10.6052/1000-0879-16-288

2016–09–05收到第1稿，2016–10–20收到修改稿.

1)国家自然科学基金(51674214)和四川省青年科技创新团队项目(2017TD0014)资助.

祝效华,张智.5-1/2 FH钻杆接头极限承载能力研究.力学与实践,2017,39(2):158-164 Zhu Xiaohua,Zhang Zhi.The ultimate bearing capacity of the 5-1/2 FH drill pipe joint.Mechanics in Engineering, 2017,39(2):158-164